Abstract
Background/Aims
Discrete choice experiments (DCEs) with either duration included an attribute or with dead included as an option can be used as a stand-alone approach to value health states. This paper reports on a DCE with both of these features to develop an EQ-5D-5L value set for Australia.
Methods
A DCE was undertaken using a large Australian panel of internet respondents, from which a sample of more than 4000 Australian adults was chosen, stratified to be population representative on age and gender. The DCE contained 500 choice triplets, with two EQ-5D-5L health states with duration, and dead as the third option. Each respondent answered 12 choice sets from the 500, stating both the best and worst options from the three available. The design was constructed to estimate a utility algorithm with main effects plus some key interaction terms. A variety of approaches to parameterising interactions, and to anchoring the value set on the required 0–1 scale, were tested. A preferred Australian adult utility algorithm for use in cost-utility analysis was then generated.
Results
In total, 4477 people completed at least one choice set and were included in the analysis. The results reflected the monotonic structure of the EQ-5D-5L, in that moving from no problems to extreme problems led to worsening utility in each dimension. Inclusion of interaction terms demonstrates that the disutility of the first dimension moving to a poor level (defined as either level 5, or level 4 or 5) had a large impact, but subsequent dimensions moving to a poor level had a relatively smaller disutility.
Discussion
This work develops a value set for the EQ-5D-5L in Australia, and also provides a range of methodological insights which can inform future work using a stand-alone DCE to value health in other countries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Country-specific value sets are important to allow decision makers to reflect the views of their community in their decisions |
The EQ-5D-5L is widely used in Australian Health Technology Assessment, and this study reports local values, which can facilitate better decisions |
Until now, decision makers either used international value sets, or the pilot Australian value set, both of which were potentially unrepresentative of true community attitudes |
1 Introduction
Cost-utility analysis (CUA) is the most prevalent form of economic evaluation and is recommended as the preferred method for the economic evaluation of new pharmaceuticals and health technologies in Australia and internationally. CUA employs the quality-adjusted life year (QALY), which combines length and quality of life, as the main measure of outcome. Preference-based measures (PBMs) of health-related quality of life (HRQoL) provide the quality-of-life input to the QALY. PBMs include a descriptive system that describes health states and a value set that provides a value for every health state described, which is typically developed using a preference elicitation method such as the time trade-off (TTO) or discrete choice experiment (DCE) with large population-based samples [1]. The most widely used PBM internationally is the EQ-5D, and value sets are available for many countries [2, 3]. The EQ-5D measures HRQoL across five dimensions (Mobility, Self-care, Usual activities, Pain/discomfort and Anxiety/depression) using three [4] or five [5] response levels. Value sets are anchored on the full health [1] to dead utility (0) scale.
The use of DCEs in health decision-making has been increasing over time [6]. One area of considerable development in recent years is the use of DCEs to value health states for the development of value sets for use in health technology assessment [7]. The relative utility of different dimensions and levels within a health state is derived from DCE tasks in line with the Random Utility Theory framework developed by McFadden [8, 9], and the utility of a health state is assumed to be the sum of the utility of each of the levels in that health state.
There has been a range of different DCE approaches taken to estimate value sets. For example, in the protocol developed by the EuroQol Research Foundation for the valuation of the EQ-5D-5L [10], both TTO and DCE data are collected, and can be combined to estimate value sets [11]. Alongside this, considerable work has been conducted to develop DCEs as a standalone approach for the estimation of value sets [7]. One methodological issue is that DCEs focusing on only health dimensions (so, comparing two health states against each other without duration or dead) result in values on a latent unanchored scale that cannot be used in the estimation of QALYs without further external anchoring. One approach that has been developed to allow latent DCE estimates to be anchored onto the full health to dead scale required for QALYs is by the inclusion of duration as an attribute in the choice sets. This approach was initially developed and tested for the valuation of the EQ-5D-3L [12, 13], the EQ-5D-5L [14] and the SF-6Dv2 [15], and a recent review found that this approach has subsequently been applied in more than 30 studies worldwide [7]. However, under this approach, the position of dead is inferred by assuming it to be the value of a health state with zero duration. However, it is unusual to actually present such a health state in these surveys, and it remains uncertain whether the inference is appropriate or not.
Beyond this key point, other ongoing methodological questions about using DCE as a health state valuation approach remain. One important question concerns the estimation of interaction effects. It is potentially extremely restrictive to assume that the impact on the value of moving between levels in a dimension of a health profile (e.g. moving from no problems to extreme problems) is independent of the levels of other dimensions in the instrument. Indeed, previous research with EQ-5D-3L has frequently demonstrated that estimation of interaction effects improves model fit, with the coefficients estimated on these terms being statistically significant. Australian data using both TTO and DCE for the EQ-5D-3L suggested that the first time a dimension moves to the worst level, there is a large disutility, but subsequent dimensions moving to the worst level have relatively smaller decrements [16, 17]. This pattern is similarly reflected in the original English EQ-5D-3L modelling [18], where the coefficient on the N3 dummy term (which equals 1 if any dimension is at the worst level) was large and statistically significant. However, it is important to note that this pattern is not universally true. For example, the study by Nicolet et al. [19] suggested that the effect of including interactions was more modest. In their data, while many of the dimension-by-dimension interactions were statistically significant, the effect on overall model fit from their inclusion is modest.
The only current Australian adult general population EQ-5D-5L value set was developed using an experimental DCE with a duration approach on a sample of 973 Australians [14]. However, an updated value set that is informed by advances in DCE methods, and is based on the preferences of a large representative sample of Australians, is required for better health care decision-making. Therefore, this paper has two key aims. First, it will produce an EQ-5D-5L value set using a DCE with a duration approach. This value set can be used in Australian health technology assessment and in the measurement of health in the community in a way that reflects underlying community values. Second, this paper will explore possible approaches to the estimation of interaction effects in the development of a value set, using a DCE approach.
2 Methods
The DCE was presented using an approach building on that employed in previous work in Australia [13]. Choice sets were presented as a series of triples, consisting of two hypothetical health states plus dead. Respondents were asked to select which of the three options was the best and which was the worst, thus giving a complete ranking over the three options.
2.1 Design of the Experiment
The design was constructed as pairs in Ngene [20], with each option in the pair consisting of a combination of an EQ-5D-5L health state and a survival duration (denoted as “TIME” below). The possible values of the duration variable were 1 year, 4 years, 7 years, 10 years and 15 years, selected to cover the range of durations included in most valuation tasks [7], but to be broad enough to allow comparison of good and bad health states. The modified Fedorov algorithm available in Ngene was used to construct the design, with the aim of producing a design with low D-error. The algorithm iterated through design improvements until no substantial reduction in the D-error was observed.
The design was built using the following criteria: (1) a dead health state was appended to each pair (options A and B) and presented as option C in each choice set; (2) the design was specified as containing 500 choice sets (from which each respondent completed 12 tasks drawn at random); (3) no prior information on parameter estimates was used (i.e. we assumed all coefficients were zero, as we did not have estimates for all of the interactions from previous studies, given the novel approaches used); (4) the experiment was designed to allow estimation of main effects, the 20 two-factor interactions between each move from full health in each dimension and the linear term on duration (which collectively allow estimation of a main effects utility algorithm, as described below in the analysis section) and 40 three-factor interactions between duration and any pair of dimensions where both appear at either level 4 or level 5; (5) the design maximised D-efficiency. To be explicit about the three-factor interactions used, the interactions involving (as an example) mobility (MO) and self-care (SC) were MO4 × SC4 × TIME, MO4 × SC5 × TIME, MO5 × SC4 × TIME, and MO5 × SC5 × TIME. As there are ten combinations of dimensions, this gives 4 × 10 (= 40) three-factor interactions. The reason that only these three-factor interactions were included is because these are the ones needed to estimate two-factor interactions in the utility algorithm; we limited ourselves to this set because previous work suggested statistically significant interactions were most prevalent between poorer levels of each dimension [13].
2.2 Administration of the Survey
The survey was hosted by Survey Engine (http://surveyengine.com/language/en/), who liaised with a panel provider (PureProfile) to arrange the sample. Pureprofile have a large pool of potential respondents across Australia, which is largely population representative in terms of key demographic variables. Evidence suggests that DCE data collected online generates similar findings to those collected face-to-face [21], and can improve the reach of the survey to those in more remote areas. Members of the PureProfile panel were sent a link to the survey, which they could then complete at their convenience. Each respondent received a small cash sum for completing the survey (approximately 10 Australian dollars). Respondents were initially screened to ensure the sample was population representative for age and gender. If their age/gender quota was incomplete (and hence they were allowed to continue), respondents completed the following: the EQ-5D-5L, the 12 DCE choice sets randomly allocated to them, feedback questions relating to clarity and difficulty of the task and their strategy for completing the DCE task, and socio-demographic questions relating to country of birth, highest education level, whether they are currently studying, their income, marital status, number of children, whether they had specific health conditions, and whether they had been hospitalised in the previous 5 years. Additionally, the survey collected data regarding how long they spent on each page, and the aggregate time across the entire survey. The study was approved by the University of Technology Sydney Human Research Ethics Committee (approval 2009‐143P).
2.2.1 Core Data Analysis
To analyse the data, we used ten different models. As described below, there were two distinct methods for using data and anchoring such that dead was valued at 0 and full health at 1. Each of these two approaches was combined with one of five different approaches to modelling interactions. The anchoring method and the approach to interactions are now described in order.
When considering the choice between two options A and B, an additive utility function with both TIME and the levels of the EQ-5D-5L would be inconsistent with the underlying QALY approach, because the QALY model implicitly requires that all health states have the same utility at death. This is the zero condition [22, 23]. Therefore, the proposed core specification of the utility function is similar to that of Bansback et al. [12], in which the utility (U) of option j in choice set s for survey respondent i was assumed to be:
where \({X}_{\text{isj}}^{^{\prime}}\) is a set of dummies relating to the levels of the EQ-5D-5L health state presented in option j and β is a corresponding vector of coefficients. The error term is a random error term with an extreme value type 1 distribution, as is usual in this setting. We adjust the standard errors using a clustered sandwich estimator to reflect the fact that survey respondents answered multiple questions. In studies such as Bansback et al. [12], the regression results are then transformed into a utility algorithm. Since the method of transformation (or scaling) is one of the questions being considered in this work, the conventional method for doing so will be described in the next section, alongside some alternative methods.
2.2.2 Anchoring
Previous work has considered different approaches to anchoring DCE data on to the 0–1 scale required for CUA [24]. The results of this existing work suggested that using preference with regard to a dead state (rather than inferring it) reduced the scale of the utility algorithm. Therefore, if preferences between health states and the dead state are included, fewer health states will be considered as worse than being dead, which has implications for health decision-making and the relative value of interventions affecting mortality and morbidity. In such a situation, interventions that improve quality of life would be valued relatively less than under an approach that yields a broader spread of values. The approach we take here is to treat the dead state as a health state with a duration of zero. Previous work, such as that of Bansback et al. [12] inferred the position of dead. Using Eq. 1 above, the value of a health state with zero duration can be inferred without requiring the respondent to actually respond to a choice set where duration is zero (i.e. a dead state). To do this, the utility function used in the initial conditional logit regression is differentiated with respect to TIME, to estimate the marginal utility of TIME. This can be done both to identify the relative disutility associated with individual levels, or with entire profiles. This gives:
To generate the utility algorithm to construct QALYs, the ratio of the marginal utility of TIME for the health state being valued and the marginal utility of TIME for full health is estimated. This is:
To do this, we do not need explicit preferences between health states and being dead. Thus, for our data, we initially only use the preference between health profiles A and B. We assume independence of irrelevant alternatives (IIA) to identify the relative preferences of respondents between the two non-dead options, which can be done for each health state (A > B if A is the best of the three or B is the worst).
However, since we have preferences between health state/duration combinations and dead, it is important to explore the effect of using those as part of the analysis. Therefore, we repeat the analysis using all data from each choice set. Specifically, we explode the stated preferences into three pairwise choices (A vs B, A vs C [dead], B vs C [dead]), and then repeat the regression analyses using all data (and with the dead health state considered as a state where TIME = 0).
2.2.3 Exploring the Effect of Including Interaction Terms
The second area explored in this paper is the approach to including interactions in the utility algorithm. Before describing the methods to do this, it is important to distinguish between interaction effects in the regression and interaction effects in the utility algorithm. As described previously, the regression fits interaction terms between duration and each move from full health in each EQ-5D-5L dimension. By estimating the 20 interaction terms between levels 2 and 5 of each dimension and duration in the regression, we can derive a main effects utility algorithm. In this study, we move beyond this to explore different approaches to including interactions in the utility algorithm. For a two-factor interaction in the utility algorithm (for example, between the worst levels of Mobility and Self-care), we need to estimate a three-factor interaction in the regression that also includes duration (for instance, MO5 × SC5 × duration), as described above.
Five different approaches to modelling interactions in the utility algorithm were explored. The first was to assume that there are no interaction terms in the utility algorithm. Second, a simple dummy was fitted to profiles where any EQ-5D dimension was at the worst level (denoted as an N5 term). Third, since previous Australian evidence suggested that our population often consider levels 4 and 5 to be close in disutility terms [13], it was considered to be of potential value to broaden the dummy to reflect any dimension at level 4 or 5 (denoted as an N45 term). When designing the experiment, we explicitly allowed for the estimation of interactions between any dimension at either level 4 or 5 with any other dimension at these same two levels. The fourth approach to interactions exploits this design characteristic, estimating the three-factor interactions between duration and each of the ten pairwise interactions between dimensions at level 5 (MO5 × SC5, MO5 × UA5, MO5 × PD5, MO5 × AD5, SC5 × UA5 and so on). Finally, the fifth interaction approach replicates this but with interactions between dimensions at either level 4 or 5. This again produces ten interactions (MO45 × SC45, MO45 × UA45, etc). To compare these different approaches, we estimate the pseudo R2, the overall direction of the interactions and their impact on the models and utility estimates.
3 Results
The characteristics of the total sample are reported in Table 1. In total, 7359 potential respondents clicked on the entry link. Of these 2245 were excluded due to being part of an age/gender quota that was already complete, leaving 5114. Of these, 4477 answered at least one choice set (with the remainder either pulling out before the first choice set or being timed out). These 4477 constitute the analysis set. Of the 4477 who completed one choice set, 4307 (96%) completed all choice sets, and of those 4307, 4267 completed all the demographics and reached the end of the task.
The distribution of time spent on each choice set is presented in Fig. 1. The median time spent on each choice set declines as respondents progress through the tasks, demonstrating increased familiarity with the task, or perhaps movement to the use of simplifying heuristics. The median respondent spent 47 s on the first choice set, but between choice sets 3 and 12, was spending approximately 20 s on each. There is a small part of the population who spend little time on each choice set; the 25th percentile falls to 10 s by the final choice set. As a robustness check, we re-estimated the simplest model (excluding dead data and only allowing two-factor interactions in the regression) excluding either the slowest or fastest 10% of respondents (or both). The impact of this was small and non-systematic across models, and is available on request from the authors.
The regression results using different approaches to modelling interaction effects are reported in Table 2 using only the relative preference between the two non-dead health states. In the simplest main effects model, the coefficients are monotonic as expected. Across all models, levels 1, 2 and 3 appear to be considered as similar, while levels 4 and 5 have significantly larger coefficients. Focusing first on the main effects model (denoted as approach 1 in Table 2), Pain/discomfort has the largest coefficient on the worst level, followed by Mobility, Self-care, Anxiety/depression and Usual activities. This pattern is similar in approaches 2 and 3, where we have introduced the N5 and N45 term, respectively. The coefficient on both new terms is negative and statistically significant at the 1% level; this suggests the effect of dimensions being at these poor levels is less than additive. In other words, the first dimension moving to a poor level has a major impact, but the second dimension and subsequent dimension moving to a poor level have a smaller effect. Interestingly, the scale of the value set reduces when interactions are included. When scaled such that dead = 0 and full health = 1, the worst health state (55555) is valued lowest under the simple main effects approach 1. Approaches 4 and 5, which include each pairwise combination of dimensions at these poor levels, rather than the crude N45 or N5 terms, produces statistically significant coefficients for seven or ten of these new interaction terms, respectively. These coefficients are positive, which shows the same effect observed in approaches 2 and 3; if multiple dimensions are at poor levels, there is a mitigation effect.
Turning to the results using dead data reported in Table 3, it is notable that many of the same patterns exist across the approaches. The results are typically monotonic across dimensions, and the effect of including interactions is to mitigate the disutility of multiple dimensions being at poor levels. The major difference between the results in Tables 2 and 3 is the scale of the resultant value sets. The value of the worst health state when the dead data are considered is between 0.282 and 0.455 better than when the dead data are excluded, depending on approach.
3.1 Selection of Preferred Model
Selection of the preferred approach for scoring EQ-5D-5L health states in Australia depends on a number of factors. Considering the inclusion or exclusion of the dead data, there are a number of considerations. First, the exclusion of the dead data uses a more uniform methodological approach to what exists, and therefore produces a value set that is more similar to most of the existing literature generating value sets for PBMs [7]. This is of value as it potentially allows comparability with other studies. In an economic evaluation context, this is useful if utility weights are drawn from multiple sources. However, it is clear that the existing method does not accurately predict preferences regarding dead [25]. This may be driven both by dead having a particular resonance with respondents that is different to a health state duration of zero [26]. It may also be a consequence of the assumptions that are made in much of the literature around constant proportional TTOs [27]. Regardless, we believe it is a potentially useful feature of a value set to be able to predict dead preferences, and this can be better achieved by including explicit choices between health states and being dead when it is reasonable to do so than by inferring the value of dead in the way that has typically been used [12].
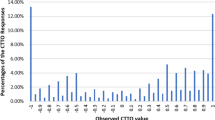
The second key issue is whether interactions should be included in the value set, and if so, how they should be specified. This is an important question for the distribution of health states in the final value set. This importance is illustrated in Fig. 2, which shows the scores of the 3125 possible health states in the EQ-5D-5L using each of the five approaches described previously. Figure 3 shows the corresponding data if dead preferences are excluded.
Models differ in terms of their spread (i.e. their minimum values), as well as the clustering of scores at different points. Of particular interest is that there is a range of scores (around 0.5–0.8) where approach 3 does not have any values; health states with the interaction term turned on lie below that range; those without the interaction term lie above. In terms of deciding between these, there is a consistent pattern in existing EQ-5D valuation sets that when interaction terms are included in the value set, they are statistically significant. However, a major issue with the use of two-factor interactions in the value set (as typified in approaches 4 and 5) is that, in some situations, the value set would mis-order health states. This occurs because the coefficients on the interaction terms are generally positive and, if enough of them are turned on when moving between states, it exceeds the main effect working in the opposite direction.
Of the models considered here, we recommend approach 2. This is because [1] interaction effects matter across approaches 2–5; [2] the inclusion of all ten interaction terms in approaches 4 and 5 yields mis-ordered scores for some pairs of health states; and [3] the distribution of health states under approach 3 is implausible, with a significant peak around 0, and very few values in the 0.5–0.8 range. The final value set resulting from approach 2 including preferences around dead health states is presented in Table 4. As an example of how this value set works, health state 23235 (i.e. level 2 for Mobility, level 3 for Self-care, level 2 for Usual activities, etc.) would be valued as 1 − 0.039 − 0.058 − 0.081 − 0.238 − 0.153 = 0.431.
4 Discussion
This paper reports the development of an EQ-5D-5L value set for Australia, and an assessment of the impact of interactions and anchoring approaches on value set characteristics. The preferred value set can now be used in health technology assessment in Australia, replacing the previous pilot version. As Australia is a user of CUA and the QALY as part of its decision-making around public subsidy of medical services and pharmaceuticals, these findings have the potential to impact significantly on resource allocation processes at the national, state and local levels (Fig. 3).
Beyond the practical value of the results, the conclusions regarding the impact of interactions on values are important in identifying the appropriate future directions for designing and modelling DCE data, and of health state data more generally. The optimal way to include interactions in data analysis is, as yet, to be determined. However, we believe that the work reported here demonstrates that analysing without consideration of interactions can be inappropriate if there is good prior reason for thinking they may impact on stated preferences of respondents. Similarly, designing a task in a way that does not allow unbiased (and reasonably precise) estimation of interaction effects is flawed as previous EQ-5D-3L valuation studies have consistently demonstrated that interactions matter [18, 28, 29], and these conclusions are supported here. The results presented here use a range of different approaches to modelling these interactions in a DCE setting. The conclusion that interactions help to predict choices matters for future valuation work using both DCE and other approaches, such as those employed in the standard approach to valuing EQ-5D health states, the EQ-VT. Future preference elicitation designs should be explicitly constructed to capture a range of interaction effects.
It is interesting to note that the value set reported here differs in a number of aspects from the pilot value set (model D) [14]. There are a number of explanations that might contribute to this difference: (1) the anchoring approach in the two studies is different, with the pilot excluding data around preferences for the dead health state; (2) the datasets were collected in different years, and preferences in the population might have changed in the intervening period; and (3) random differences caused by recruiting different samples. Our data do not allow these to be easily disentangled, but we believe that the more contemporary, larger dataset reported here, which is based on data that directly observes whether a health state is better or worse than dead, is more appropriate and hence should be used in preference to the value set reported in the pilot work.
The research described here has a number of potential limitations. Whilst the findings from this study may be of interest more generally to the use of DCE duration with any utility instrument, all analysis is conducted using the EQ-5D-5L instrument and may therefore be specific to this context. Second, the findings are specific to an online Australian adult general population sample. Clearly, internet use is high in Australia, particularly in younger, or more highly educated, people, but we acknowledge that there is a significant potential selection issue in the use of internet panels (as there may also be with those willing to take part in a face-to-face interview). We have controlled for age and gender, but note that there may be both observable and unobservable differences between our sample and the general population. A related point is that our preference elicitation approach is potentially too difficult for those with cognitive impairment. If we seek the preferences of a representative sample, it may be that we cannot do so for those unable to complete the DCE task online. This is an issue for face-to-face interviews as well, but clearly, not having an interviewer to guide the respondent will (all other things being equal) reduce the pool of people able to complete it. A further issue with the use of a DCE to value EQ-5D-5L health states is that it is different to valuation approaches used in other settings, which have typically combined both a DCE and a composite time trade-off (cTTO). It is likely that TTO and DCE yield different results, and it is challenging to identify which is more reflective of population preferences given the lack of an external validation process. Thus, while we believe that the value set reported here captures the preferences of Australian adults for health defined within the EQ-5D-5L, it is important to note that the results are not directly comparable to those derived using other valuation approaches. Finally, the value set we are recommending is sensitive to the choice to include or exclude data around dead (and hence the appropriate method for anchoring on the necessary 0–1 scale). While we believe there is merit in having a value set that predicts respondents’ attitudes to dead, it should be acknowledged that such questions may be difficult or unethical to ask in some populations, and there are additionally methodological questions around the use of a dead health state in a random utility theory context [26].
To summarise, we have developed a value set for use in Australian health care decision-making. We believe that the findings in this paper suggest that including interaction effects means that the values used in decision-making more accurately reflect the preferences of the Australian population, rather than reliance on findings from different countries, or from our older pilot data, which were based on a smaller sample size.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Change history
03 March 2023
Missing Open Access funding information has been added in the Funding Note
References
Brazier J, Ratcliffe J, Salomon JA, Tsuchiya A. Measuring and valuing health benefits for economic evaluation. Oxford: Oxford University Press; 2007.
Devlin NJ, Shah KK, Feng Y, Mulhern B, van Hout B. Valuing health-related quality of life: an EQ-5D-5L value set for England. Health Econ. 2018;27(1):7–22.
Pickard AS, Law EH, Jiang R, Pullenayegum E, Shaw JW, Xie F, et al. United States valuation of EQ-5D-5L health states using an international protocol. Value Health. 2019;22(8):931–41.
Brooks R. EuroQol: the current state of play. Health Policy. 1996;37(1):53–72.
Herdman M, Gudex C, Lloyd A, Janssen MF, Kind P, Parkin D, et al. Development and preliminary testing of the new five-level version of EQ-5D (EQ-5D-5L). Qual Life Res. 2011;20(10):1727–36.
de Bekker-Grob EW, Ryan M, Gerard K. Discrete choice experiments in health economics: a review of the literature. Health Econ. 2012;21(2):145–72.
Mulhern B, Norman R, Street DJ, Viney R. One method, many methodological choices: a structured review of discrete-choice experiments for health state valuation. Pharmacoeconomics. 2019;37(1):29–43.
McFadden D. Conditional logit analysis of qualitative choice behaviour. In: Zarembka P, editor. Frontiers in econometrics. New York: Academic Press; 1974. p. 105–42.
McFadden D. Econometric models of probabilistic choice. In: Manski C, McFadden D, editors. Structural analysis of discrete data with economic applications. Boston: MIT Press; 1981. p. 422–34.
Oppe M, Devlin NJ, van Hout B, Krabbe PF, de Charro F. A program of methodological research to arrive at the new international EQ-5D-5L valuation protocol. Value Health. 2014;17(4):445–53.
Ramos-Goni JM, Craig B, Oppe M, Van Hout B. Combining continuous and dichotomous responses in a hybrid model (report number 16002). 2016.
Bansback N, Brazier J, Tsuchiya A, Anis A. Using a discrete choice experiment to estimate societal health state utility values. J Health Econ. 2012;31:306–18.
Viney R, Norman R, Brazier J, Cronin P, King MT, Ratcliffe J, et al. An Australian discrete choice experiment to value eq-5d health States. Health Econ. 2014;23(6):729–42.
Norman R, Cronin P, Viney R. A pilot discrete choice experiment to explore preferences for EQ-5D-5L health states. Appl Health Econ Health Policy. 2013;11(3):287–98.
Norman R, Viney R, Brazier J, Burgess L, Cronin P, King MT, et al. Valuing SF-6D health states using a discrete choice experiment. Med Decis Mak. 2014;34(6):773–86.
Viney R, Norman R, Brazier J, Cronin P, King MT, Ratcliffe J, et al. An Australian discrete choice experiment to value EQ-5D health states. Health Econ. 2013;23:729–42.
Viney R, Norman R, King MT, Cronin P, Street D, Knox S, et al. Time trade-off derived EQ-5D weights for Australia. Value Health. 2011;14:928–36.
Dolan P. Modelling valuations for EuroQol health states. Med Care. 1997;35(11):1095–108.
Nicolet A, Groothuis-Oudshoorn CGM, Krabbe PFM. Does inclusion of interactions result in higher precision of estimated health state values? Value Health. 2018;21(12):1437–44.
ChoiceMetrics. Ngene user manual and reference guide version 1.2. 2018.
Mulhern B, Longworth L, Brazier J, Rowen D, Bansback N, Devlin N, et al. Binary choice health state valuation and mode of administration: head-to-head comparison of online and CAPI. Value Health. 2013;16(1):104–13.
Bleichrodt H, Johannesson M. The validity of QALYs: an experimental test of constant proportional tradeoff and utility independence. Med Decis Mak. 1997;17(1):21–32.
Bleichrodt N, Wakker P, Johannesson M. Characterizing QALYs by risk neutrality. J Risk Uncertain. 1997;15(2):107–14.
Norman R, Mulhern B, Viney R. The impact of different DCE-based approaches when anchoring utility scores. Pharmacoeconomics. 2016;34:805–14.
Norman R, Mulhern B, Viney R. The impact of different DCE-based approaches when anchoring utility scores. Pharmacoeconomics. 2016;34(8):805–14.
Flynn TN, Louviere JJ, Marley AA, Coast J, Peters TJ. Rescaling quality of life values from discrete choice experiments for use as QALYs: a cautionary tale. Popul Health Metr. 2008;6:6.
Jonker MF, Donkers B, de Bekker-Grob EW, Stolk EA. Advocating a paradigm shift in health-state valuations: the estimation of time-preference corrected QALY tariffs. Value Health. 2018;21(8):993–1001.
Badia X, Roset M, Herdman M, Kind P. A comparison of United Kingdom and Spanish general population time trade-off values for EQ-5D health states. Med Decis Mak. 2001;21(1):7–16.
Tsuchiya A, Ikeda S, Ikegami N, Nishimura S, Sakai I, Fukuda T, et al. Estimating an EQ-5D population value set: the case of Japan. Health Econ. 2002;11(4):341–53.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. Funding was supported by National Health and Medical Research Council.
Author information
Authors and Affiliations
Contributions
All authors: Substantial contributions to the conception and design of the work, revised work critically for important intellectual content, approved the version to be published, agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Corresponding author
Ethics declarations
Conflict of interest
RN, BM, PL, DS and RV are members of the EuroQol Group, developers of the EQ-5D-5L.
Consent to participate
All participants freely gave informed consent to participate in the study, and to have their data used to develop the results contained in this paper.
Ethical approval
Ethics was approved through the University of Technology Sydney Human Research Ethics Committee.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Norman, R., Mulhern, B., Lancsar, E. et al. The Use of a Discrete Choice Experiment Including Both Duration and Dead for the Development of an EQ-5D-5L Value Set for Australia. PharmacoEconomics 41, 427–438 (2023). https://doi.org/10.1007/s40273-023-01243-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40273-023-01243-0