FormalPara Key Points for Decision Makers

Uncertainty surrounding the costs and effects in cost-effectiveness analysis is typically described using the cost-effectiveness acceptability curve (CEAC), which may not be appropriate to inform decision makers who are risk averse.

Decision makers who may need to meet budgetary constraints and health outcome targets may be naturally risk averse towards both costs and effects.

The present paper introduces the cost-effectiveness risk-aversion curve that penalizes the expected net benefit of a program for its downside deviation for a wide range of threshold cost-effectiveness ratios, and may provide an alternative helpful tool to inform risk-averse decision makers.

1 Introduction

Cost-effectiveness analysis of health care interventions has been advocated and widely adopted as a tool to help policy and decision makers in setting priorities for resource allocation [1]. The analytical decision criterion in cost-effectiveness analysis is the incremental cost-effectiveness ratio (ICER), i.e. the difference in costs divided by the difference in effects between two or more mutually exclusive treatment strategies [2, 3]. This decision rule follows from a linear programming approach to solving a constrained optimization problem where aggregate health outcomes are maximized subject to a budget constraint [2, 4,5,6]. Following this decision rule, programs are ranked according to their ICER and implemented in ascending order, until the budget is exhausted. The ICER of the last implemented program then represents the shadow price of the constrained budget.

This decision rule has been introduced under conditions of certainty, i.e. in the absence of uncertainty associated with costs and effects [2]. However, costs and effects are subject to stochastic variability and much research interest has focused on how to deal with uncertainty in cost-effectiveness analysis [7,8,9,10,11,12]. The two most widely used methods are the cost-effectiveness acceptability curve (CEAC) and net monetary benefits (NMB) [6, 7]. While the CEAC summarizes the joint distribution of incremental costs and effects on the cost-effectiveness plane (CEP), displaying the probability that the intervention is cost effective for a wide range of threshold cost-effectiveness ratios (λ), the NMB approach linearly transforms the costs and effects of health interventions by multiplying the effects of an intervention with the threshold cost-effectiveness ratio (λ) and subtracting the costs thereof. This facilitates statistical analysis of the results of a cost-effectiveness analysis, and the probability that a program has the highest expected NMB can be calculated.

However, both approaches do not incorporate the decision maker’s preferences over expected return and risk when choosing between treatment alternatives. O’Brien and Sculpher were the first to introduce the idea of considering an investment in a health care program as an investment in a risky asset, and suggested to elicit the decision-maker’s trade-off between expected return and risk for ranking health care programs in the presence of uncertainty [13]. If a decision maker was risk neutral, he would solely base his decision on the expected ICER or expected NMB, and the analysis of uncertainty would be irrelevant [14]. However, decision makers may be risk averse towards costs and effects [13, 15,16,17,18]. Since health is not a transferable good, decision makers may be risk averse towards health outcomes [18]. In addition, a sub-societal decision maker, such as a third-party payer, may also be risk averse towards costs as budgetary constraints must be met [11, 19]. The risk of ending up with lower-than-expected health outcomes or exceeding the expected budget may therefore be relevant for rational decision makers with risk aversion.

Methods developed in financial economics to handle different investment opportunities with uncertain outcomes may offer an armamentarium to deal with uncertainty in cost-effectiveness analysis. One possibility to facilitate comparison of health care programs with different risk-return characteristics, without requiring to explicitly derive a utility function over expected return and risk, is to construct a risk-adjusted league table of expected returns using a modification of the Sharpe ratio that describes the extra return we may achieve per unit of risk [20, 21]. This approach assumes that a risk-averse decision maker prefers higher expected returns per unit of risk, ceteris paribus. However, one limitation of this method is that it does not distinguish between good and bad risks. While a program’s performance above expected returns may be desirable (good risk), risk aversion only applies to outcomes that fall below expected returns (bad risk). Furthermore, good risk is already accounted for in estimating expected returns, as programs with the same downside variation but different upside variations will also have different expected returns. In the present paper we therefore present a risk-adjusted approach to handle uncertainty in cost-effectiveness analysis that explicitly incorporates bad risk in decision making.

2 Uncertainty in Cost-Effectiveness Analysis

Since incremental costs and effects may be subject to uncertainty, the interpretation of confidence intervals for ICERs may be ambiguous. The ICER may include negative values that may stem from negative incremental costs, indicating cost savings (which is desirable), or from negative incremental effects, indicating a loss in health outcomes (which is not desirable) [8, 12, 22, 23]. Furthermore, a positive ICER may result from an intervention that frees resources but leads to lower health outcomes, or from an intervention that costs more and is more effective. This ambiguity has led to the development of the CEAC, which estimates the probability that the joint distribution of incremental costs and effects of an intervention falls below the threshold value λ, which is usually interpreted as the decision maker's maximum willingness to pay (WTP) per health outcome [22]. The joint distribution of incremental costs and effects is first plotted on the CEP, and the probability that the intervention is cost effective is then estimated as a function of λ, denoting a line through the origin of the CEP, which is rotated anticlockwise [7, 12].

However, the CEAC provides no information about the magnitude of ‘bad’ outcomes, i.e. all outcomes that exceed λ are treated as equally bad. To make our conceptual point, consider the two health care programs A and B (scenario 1), as indicated in Table 1. Both programs have the same mean costs ($60,000) and effects (10 quality-adjusted life-years [QALYs]), but program A exhibits higher variability in costs and effects than program B. The joint distribution of total costs and effects for each program are shown in Fig. 1. A risk-neutral decision maker would be indifferent between the two programs; however, decision makers may be naturally risk averse towards outcomes that may exceed λ. As can be seen from Fig. 1, program A exhibits a greater downside variation of health outcomes (outcomes that fall in the south-west and south-east quadrants), as well as an upside variation of costs (outcomes that fall in the north-east and south–east quadrants). Whereas outcomes in the south–east quadrant are not desirable, the nature of the outcomes in the north–east and south–west quadrants depends on the trade-off between costs and effects, as determined by λ.

Table 1 Costs and effects of six hypothetical health care programs
Full size table
Fig. 1
figure 1

Bivariate 95% credible ellipses for costs and effects. The 95% credible ellipses for two programs with identical mean costs ($60,000) and effects (10 QALYs) are shown. Program A has a higher variability in costs and effects than program B (scenario 1 in Table 1), QALY quality-adjusted life-year, NW north–west, NE north–east, SW south–west, SE south–east

Full size image

NMBs have been introduced to address the limitations of ratio statistics by linearly transforming the costs and effects for each intervention. The average NMB for each intervention can be estimated as µE λ − µC, where µE denotes the mean effects, µC denotes the mean costs, and λ denotes the threshold ratio. The distributions of the NMB for programs A and B, assuming λ = $50,000/QALY, are shown in Fig. 2. Since costs and effects for programs A and B are normally distributed in our example, the NMB of the two interventions are also normally distributed with a mean of $440,000. As can be seen from Fig. 2, program A exhibits a higher downside variation of NMB than program B, indicating that the magnitude of potentially bad outcomes is higher.

Fig. 2
figure 2

Boxplot of NMB at lambda $50,000/QALY. The distribution of NMB for program A shows a higher downside (and upside) variation than program B (scenario 1 in Table 1). NMB net monetary benefit, QALY quality-adjusted life-year

Full size image

Note that this information is not provided by the joint distribution of incremental costs and effects on the CEP. From the joint distribution on the CEP, as shown in Fig. 3, estimated by sampling 10,000 times from the distributions for the costs and effects defined in Table 1 (scenario 1), we are unable to disentangle whether program A or program B exhibits a higher downside variation, or ‘bad risk’, since for two normal distributions the variance of the mean difference is the sum of the variance of each individual distribution, i.e. information about the variance of each individual distribution is lost on the CEP. However, the variance of costs and effects of each individual program is important for a risk-averse decision maker for choosing between program A and program B. Furthermore, the CEAC for A versus B, as shown in Fig. 4, only informs us about the probability that each program is cost effective, irrespective of the downside variation of the NMB of the individual programs. The CEAC in our hypothetical example corresponds to a horizonal line at 0.5, and provides no information about the magnitude of the downside variation of the two programs that are compared. Following the CEAC, a decision maker would be indifferent between program A and program B.

Fig. 3
figure 3

Cost-effectiveness plane (program A versus program B). Joint distribution of incremental costs and effects of program A versus program B (scenario 1 in Table 1). The 95%, 50%, and 5% credible ellipses are shown. QALY quality-adjusted life-year

Full size image
Fig. 4
figure 4

CEAC (program A versus program B). The CEAC corresponds to a horizonal line at 0.5 for all threshold ratios, suggesting equality of programs A and B. CEAC cost-effectiveness acceptability curve, WTP willingness to pay, QALY quality-adjusted life-year

Full size image

3 The Sortino Ratio

In financial economics, a number of methods have been developed to adjust the expected return of an investment in a risky asset for its volatility, since the future returns in stocks and bonds are uncertain. The most widely known measure is the Sharpe ratio, which has been introduced by Nobel Prize laureate William F. Sharpe [21]. The Sharpe ratio is the average return earned in excess of the risk-free rate per unit of volatility of an asset. The greater the value of the Sharpe ratio, the more extra return we earn per unit of risk. The Sharpe ratio has also been named the reward-to-variability ratio and its application in health care finance has been discussed previously [20]. However, a limitation of the Sharpe ratio is that it measures total volatility of an asset, while naturally risk-averse investors are usually only concerned with the downside risk of an asset, since the upside volatility of an asset is considered desirable.

The Sortino ratio addresses this limitation of the Sharpe ratio and only considers the downside risk in evaluating the risk-return characteristics of an asset [24, 25]. The Sortino ratio S is defined as (Eq. 1):

$$S=\frac{\stackrel{-}{R\mathrm{p}}-\mathrm{TR}}{\mathrm{DD}}$$
(1)

where \(\stackrel{-}{Rp}\) denotes the mean return of the portfolio, TR denotes the target return or minimal acceptable return, and DD denotes the downside deviation, where (Eq. 2)

$$\mathrm{DD}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left({R\mathrm{p}}_{i}-\mathrm{TR}\right)}^{2}f\left(t\right)}$$
(2)
$$f\left( t \right) = 1\;{\text{if}}\;R{\text{p}}_{i} < {\text{TR}}$$
$$f\left( t \right) = 0\;{\text{if}}\;R{\text{p}}_{i} \ge {\text{TR}}$$

The DD is the root-mean-square of the downside deviations of the portfolios return from the target return where all returns above the target return are set to zero. The target return may be based on expected returns using historical data, but an investor could define any target return below which a portfolio’s return would be treated as underperformance. Note that the DD divides the variance of bad risks by all observations (n) and not only those that exhibit a downside variation. The smaller the number of observations with downside risk, the smaller the DD will be. Furthermore, the smaller the deviation of the portfolio’s return from the target return, the smaller the DD will be. The Sortio ratio therefore informs us about the expected return per unit of bad risk, i.e. investments with a higher Sortino ratio are preferable over investments with a lower Sortino ratio, i.e. investments are penalized for the bad risk associated with it.

4 The Net Benefit-to-Risk Ratio

In health care finance, we can also define downside risk as the risk of experiencing an NMB below the expected NMB (or a target NMB) of a program. If we consider a health care program as an investment in a risky asset, since costs and effects are uncertain, we can penalize expected NMB for the bad risk associated with those respective programs and define a net benefit-to-risk ratio SNMB, as shown in Eq. 3:

$${S}_{\mathrm{NMB}}=\frac{{\mu }_{\mathrm{NMB}}}{{\mathrm{DD}}_{\mathrm{NMB}}}$$
(3)

where µNMB denotes the expected NMB of a program and DDNMB denotes its downside deviation. The DDNMB can be written as (Eq. 4):

$${\mathrm{DD}}_{\mathrm{NMB}}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left({\mathrm{NMB}}_{i}-{\mu }_{\mathrm{NMB}}\right)}^{2}f\left(t\right)}$$
(4)
$$f\left( t \right) = 1\;{\text{if}}\;{\text{NMB}}_{i} < \mu _{{{\text{NMB}}}}$$
$$f\left( t \right) = 0\;{\text{if}}\;{\text{NMB}}_{i} \ge \mu _{{{\text{NMB}}}}$$

where NMBi denotes a sample observation, e.g. from bootstrapping mean costs and effects of a program. For all bootstrap samples, the expected NMB (µNMB) is subtracted thereof and set to zero if it is positive (i.e. overperformance). For all samples where the NMB falls below the expected NMB, we estimate the difference and square it. The root of the mean squared differences of all sample observations corresponds to the DDNMB, in analogy to the downside risk of the Sortino ratio. Hence, the expected NMB of a program, µNMB, is penalized for the bad risk associated with it. Note that DDNMB will be higher if either the number of observations n below µNMB is higher and/or the magnitude of deviations below µNMB is higher. When estimating the mean NMB within the context of a clinical trial, the number of samples that fall below µNMB is usually 50% due to the central limit theorem. However, in a modeling study that estimates the cost effectiveness of health care interventions, the distribution of the sample observations around the µNMB may be asymmetrical.

A risk-averse decision maker would prefer a health care program with a higher net benefit-to-risk ratio SNMB, ceteris paribus. It may be argued that the value of the decision-maker's maximum WTP (λ) per unit of health outcome is not known. However, the net benefit-to-risk ratio can be calculated for a wide range of threshold ratios, as is usually also done when constructing the CEAC. The resulting curve may be defined as the cost-effectiveness risk-aversion curve (CERAC) as it explicitly incorporated risk aversion into the analysis.

For a stylized example, consider again the two health care programs listed in Table 1 (scenario 1). Program A exhibits a higher variability than program B for both costs and effects. This translates into a higher downside deviation DDNMB of the NMB, which is shown in Fig. 2, for a threshold ratio of $50,000/QALY. The expected NMB for both programs A and B is $440,000; however, the DDNMB for program A is $35,648, whereas for program B it is $26,557. This translates into a net benefit-to-risk ratio of 12.4 and 16.6, respectively. Program B therefore offers more expected return per unit of bad risk, the incremental net benefit-to-risk ratio being 4.2, indicating that program B yields, on average, 4.2 NMB more per unit of bad risk than program A, assuming λ = $50,000/QALY.

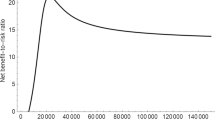
Calculating the net benefit-to-risk ratio SNMB for each individual program and for all possible λ, allows us to construct the CERACs (Fig. 5). From Fig. 5 it becomes obvious that program B offers more expected NMB per unit of bad risk for all possible λ and should therefore be preferred by a risk-averse decision maker. The distance between the two CERACs reflects the incremental net benefit-to-risk ratio. Note that any negative net benefit-to-risk ratio is the result of a negative NMB, as the downside risk of the NMB of a health care program is always positive by definition. The CERAC therefore cuts the x-axis where the expected NMB turns to zero, but could be extended to include negative values. The CERAC is monotonically increasing and horizontally asymptotes to the ratio of the slopes of the expected NMB and DDNMB lines when plotted against λ as λ increases.

Fig. 5
figure 5

CERAC. The CERAC for programs A and B shows that the net benefit-to-risk ratio for program B is always preferred to program A for all threshold ratios. The CERAC cuts the x-axis when the expected NMB exceeds zero. CERAC cost-effectiveness risk-aversion curve, NMB net monetary benefit, WTP willingness to pay, QALY quality-adjusted life-year

Full size image

5 A Further Example

We have used a very simplistic example above to illustrate that the joint distribution of incremental costs and effects on the CEP and CEAC do not provide sufficient information for a risk-averse decision maker for choosing between programs with the same expected NMB but different downside variation, whereas the CERAC indeed helps us to distinguish between programs with different risk-return characteristics. We now illustrate two scenarios where the program with the higher expected NMB may have the lower net benefit-to-risk ratio, and vice versa.

Consider scenario 2 as shown in Table 1. Program D is now compared with program C, the mean incremental cost is $100,000 and the mean incremental effect is 5 QALYs, with the mean ICER being $20,000/QALY gained. Hence, at a threshold ratio greater than $20,000/QALY, a risk-neutral decision maker would prefer program D over program C. The joint distribution of incremental costs and effects, as shown in Fig. 6, has been estimated by sampling 10,000 times from the distributions for costs and effects as defined in Table 1 (scenario 2). For this sampling exercise, we have truncated the normal distribution at zero to exclude negative values for costs and effects. The corresponding CEAC in Fig. 7 shows that at a threshold ratio greater than $20,000/QALY, program D becomes the preferred strategy, with a higher probability of being cost effective. However, by summarizing the joint distribution of incremental costs and effects using the CEAC, we cannot tell which program has the greatest downside variation with respect to costs and effects. From Table 1 (scenario 2), it is obvious that program D has a much greater variation for both costs and effects than program C. The CERAC therefore favors program C over program D for all threshold ratios (Fig. 8), although program D has a higher expected NMB for threshold ratios greater than $20,000/QALY.

Fig. 6
figure 6

Cost-effectiveness plane (programs D/F versus programs C/E). Joint distribution of the incremental costs and effects of programs D/F versus programs C/E (scenarios 2 and 3 in Table 1). The 95%, 50%, and 5% credible ellipses are shown. Both scenarios lead to the same joint distribution on the cost-effectiveness plane. QALY quality-adjusted life-year

Full size image
Fig. 7
figure 7

CEAC (programs D/F versus programs C/E). Scenarios 2 and 3 (Table 1) both lead to the same CEAC. CEAC cost-effectiveness acceptability curve, WTP willingness to pay, QALY quality-adjusted life-year

Full size image
Fig. 8
figure 8

CERAC (program C versus program D). Program C exhibits a higher net-benefit ratio for all threshold ratios compared with program D (scenario 2 in Table 1). CERAC cost-effectiveness risk-aversion curve, WTP willingness to pay, QALY quality-adjusted life-year

Full size image

As a contrasting example, consider now scenario 3 (Table 1). The expected costs and effects of the two programs to be compared are identical to those in scenario 2, but now with reversed uncertainties, i.e. standard deviation of costs and effects for program E is greater than for program F (Table 1, scenario 3). The joint distribution of incremental costs and effects of program F versus program E is identical to that of program D versus program C (Fig. 6) and therefore leads to the same CEAC (Fig. 7). This is because the variance of the incremental distribution for costs and effects is the sum of the variances of the two programs to be compared. However, since program E now has a much greater standard deviation for costs and effects than program F, the CERAC now favors program F over program E for threshold ratios greater than $8561/QALY where the two CERACs cross (Fig. 9). That is, scenarios 2 and 3 lead to the same CEAC but vastly different CERACs. Furthermore, note that program F becomes the preferred program, compared with program E, at a lower threshold ratio than if we were to use the expected NMB as a decision criterion ($8561 vs. $20,000 per QALY).

Fig. 9
figure 9

CERAC (program E versus program F). The two CERACs cross at $8561/QALY, where program F becomes the preferred strategy. Below a threshold ratio of $8561/QALY, program E is the preferred strategy, with a higher net benefit-to-risk ratio. CERAC cost-effectiveness risk-aversion curve, WTP willingness to pay, QALY quality-adjusted life-year

Full size image

6 Discussion

Much research interest has focused on handling uncertainty in cost-effectiveness analysis. While most approaches elaborate on how uncertainty can be described in cost-effectiveness analysis, the explicit incorporation of risk aversion in decision making has gained much less attention [11, 13, 15,16,17,18, 26]. However, risk aversion towards big losses may be a rational behavior that merits more attention as health is generally considered as the highest good of mankind.

Different authors have motivated the perspective of a risk-averse decision maker at the societal and subsocietal level. Ben-Zion and Gafni [18] argue that health is not a transferable good, as is the case with other public investment opportunities, e.g. patients with loss of vision due to diabetic retinopathy cannot ‘share’ their disease with other individuals. Furthermore, those who benefit from health care cannot share their benefit with other individuals. Since diseases and the benefit of health care accrue to individuals and are not transferable, decision makers at the societal level may therefore be risk averse towards health outcomes [18, 27]. O’Brien and Sculpher argue that most health care managers operate at a subsocietal level and have to meet budgetary constraints as well as outcome performance targets [13]. Hence, health care managers at insurance companies for example who need to allocate available resources are naturally risk averse towards both costs and effects. This is in line with the cost-containment and reduction strategies of most health insurance companies when considering whether health care interventions for patients should be paid for or not [19]. Even though risk aversion towards costs and effects may seem to be a rational behavior, current approaches to handle uncertainty in cost-effectiveness analysis do not take this into account. The CEAC provides no information about the risk-return characteristics of the individual programs and only informs us about probabilities in the sense of frequentist or Bayesian statistics when comparing costs and effects of two treatment strategies [12, 28].

One reason for the limited use of methods to analyze the results of a cost-effectiveness analysis under risk aversion may be that a preference function over expected return and risk is usually needed. For example, O’Brien and Sculpher assume a concave utility function over expected return and risk, implying a diminishing marginal rate of substitution between expected return and reduced risk, without explicitly specifying such a utility function [13]. Zivin suggested a model where costs are certain and effects uncertain, and modeled a linear mean-variance utility function with constant absolute risk aversion over health effects [16]. Although this approach may seem plausible and assumes risk neutrality towards costs, it assumes a utility function over the mean-variance dimensions of health effects. However, decision makers are rarely explicit about their utility function over uncertain costs and effects, and the explicit elicitation of such preferences may prove to be a difficult task in practice. Similarly, in an alternative model considering risk aversion in cost-effectiveness analysis, Elbasha assumes a negative exponential utility function over NMB, thereby including both uncertain costs and effects into the analysis [17]. Although this model considers both uncertain costs and effects, it also requires that a utility function is assumed that should reflect the decision maker’s risk attitude, which might be difficult to elicit in practice. In the paper by Al et al., the decision rule of cost-effectiveness analysis has been discussed in the presence of uncertain costs and effects [11]. Al et al. emphasized the difficulty of specifying a decision maker’s explicit utility function over uncertain costs and effects, and suggested different approaches to handle risk aversion in cost-effectiveness analysis. For example, within the context of optimization problems, expected health outcomes may be maximized, with a limited risk of exceeding the budget, implying risk neutrality towards health outcomes and risk aversion towards costs [11]. Alternatively, assuming risk neutrality towards costs and risk aversion towards health outcomes, expected costs may be minimized subject to the constraint that the probability of some aspiration level for health outcomes may be exceeded with a high probability [11]. Constrained optimization in the presence of uncertain costs and effects is a useful tool to analyse different budget allocation scenarios and their impact on aggregate overall health [11, 29]. However, constrained optimization may also imply preference functions over uncertain costs and effects and their practical application may be difficult. Furthermore, constrained optimization assumes that information on uncertain costs and effects is available for all programs, which is rarely the case in practice.

An alternative to specifying a preference function over uncertain costs and effects is to use risk-adjusted performance measures. Their use in finance has become standard repertoire for analysing risky assets and they do not require the analyst to elicit a preference function over expected return and risk [21, 24, 25]. Risk-adjusted performance measures assume that the investor is risk averse and prefers higher expected returns per unit of risk, ceteris paribus. However, risk may be classified as ‘good risk’ and ‘bad risk’. While overperformance may be desirable (i.e. good risk), risk aversion only applies to bad risk, i.e. the probability of underperforming relative to some outcome targets. The application of risk-adjusted performance measures in health care, considering overall risk, has been discussed previously [20]. However, in health care finance, it seems counterintuitive to penalize expected net benefits for upside risk, as does the Sharpe ratio. In addition, it should be noted that the Sharpe and Sortino ratios may lead to the same ranking of investment opportunities when returns are normally distributed, but this is not necessarily the case when return on investment follows a skewed distribution. In the present paper, we therefore only considered downside risk, as this is the only component of risk where risk aversion applies. In addition, penalizing expected NMB for downside deviation also seems to be in line with the concept of loss aversion or endowment effect, as empirical evidence suggests that individuals and decision makers weigh losses higher than equivalent gains [30,31,32,33].

Using risk-adjusted performance measures as opposed to preference functions such as utility functions or prospect theory value functions [34] may seem to represent an ad hoc approach to handling the risk-return characteristics of programs in health care finance. To this end, it should be noted that preference functions as well as risk-adjusted performance measures both represent mathematical approaches to handle the risk and return characteristics of different investment opportunities [35]. Hence, whereas preference functions require that a decision maker is explicit about his preferences over uncertain costs and effects, risk-adjusted performance measures imply a preference function without being explicit about such a function. In a study by Plantinga and de Groot, the authors compared the rank correlation of different risk-adjusted performance measures with explicit preference functions such as the quadratic utility function or different prospect theory value functions with varying levels of risk aversion [35]. The authors found that the Sortino ratio correlated well with intermediate to high levels of risk aversion, whereas the Sharpe ratio better corresponded to low levels of risk aversion [35]. However, empirical research in health care finance is needed to evaluate what preference function best matches the net benefit-to-risk ratio and is implicit in using the CERAC. To this end, moving away from the assumption of risk neutrality in health care finance towards risk-adjusted approaches to handle uncertainty in cost-effectiveness analysis seems to be reasonable in many settings faced with budget constraints and the need to meet health outcome targets [13].

7 Conclusion

We believe the CERAC is a useful instrument to inform decision makers with risk aversion. It can be easily extended to compare multiple health care interventions and allows to quantify downside risk in a meaningful way without requiring an explicit utility function. In addition, it is straightforward to integrate in practice when analysing uncertainty in cost-effectiveness analysis of health care interventions.