FormalPara Key Points for Decision Makers

Deterministic one-way sensitivity analysis has a number of limitations and can provide biased and incomplete information.

Probabilistic one-way sensitivity analysis overcomes the shortcomings of deterministic sensitivity analysis.

1 Introduction

During the last 2 decades, comprehensive probabilistic sensitivity analysis (PSA) has become the recommended approach to examining impact of parameter uncertainty on the outputs of cost-effectiveness analyses (CEAs). This said, one-way sensitivity analysis (OSA) continues to be recognised as a popular form of uncertainty analysis for CEAs. Drummond et al. [1] describes the process of OSA as follows: “single values for each of the input parameters are used to estimate the expected cost, effect and [net benefit (NB)] based upon their mean values. The parameter values are varied and the effect on model outputs are reported.” (p. 393). All of these guides note that deterministic one-way analysis does not provide insight into the decision uncertainty that concerns decision makers. Further criticisms of OSA include that (a) the range of values chosen is often arbitrary; (b) deterministic approaches will not take account of any correlations and non-linearities in the model, which means they will produce biased estimates of the expected costs and outcomes; and (c) the results do not tell the decision maker how likely it is that a specific value or range of values will be observed. Critics have also observed that the conventional way of reporting OSA—the tornado diagram—is problematic because the range covered by the bars can easily be misinterpreted; for example, the proportion of the bar that is in the positive NB space does not indicate the probability that the parameter will take a value that would produce a positive NB. In addition, tornado diagrams frequently use the incremental cost-effectiveness ratio (ICER) rather than NB as the scale for the horizontal axis, which introduces further complications as ICERs are neither continuously nor uniquely defined.

Problems with the conventional approaches to OSA do not alter decision makers’ legitimate concern that changes in one particular parameter in the decision problem may impact on the expected value of a technology. As Claxton et al. [2] observed in 2005, “in making an assessment of the implications of decision uncertainty when issuing guidance, the Appraisal Committee will also need an understanding of the contribution of specific parameters (or combinations of parameters)”. They go on to suggest that the value of information can meet this need. However, the expected value of knowing something with certainty is not the same as knowing what the impact of an input parameter taking a specific value will be on the expected costs, outcomes and incremental NB, i.e. value-of-information methods do not meet the decision makers’ information requirements that OSA is designed to. Drummond et al. [1] reported that once a threshold value has been identified, the probability of that value being observed can be calculated and reported (p395). Awotwe et al. [3] described a probabilistic version of tornado diagrams, constructed using the data created by expected value of perfect parameter information (EVPPI) analysis. Subsequently, Hill et al. [4] described a probabilistic approach to threshold analysis for CEA. The latter methods are particularly computationally intensive, and the approach described by Drummond and colleagues provides the decision maker with considerably less information.

In this paper, we describe how to implement probabilistic one-way sensitivity analysis (POSA) using a more efficient approach than the EVPPI process used by Awotwe et al. [3]. We then propose an alternative graphical presentation for the outputs of this analysis—the POSA line graph, which addresses some of the weaknesses of tornado diagrams and allows the identification of threshold values referred to by both Drummond et al. [1] and Hill et al. [4].

OSA examines the impact on the predicted costs and outcomes of changing the value of a specified variable while holding all other variables constant at their expected value. The intent of undertaking OSA is to support the decision maker to consider the question, ‘What if the specified variable took a different value from the expected value used in the analysis?’.

Given that we are almost never certain of the true value of any parameter included in an economic evaluation, this is a sensible question for any decision maker to consider. However, there are two problems with the way that OSA addresses the question.

First, holding the value of all other parameters constant at their expected values assumes that the values of all parameters are independent of each other. For example, if the cost of managing an adverse event is higher than the cost used in the base-case analysis, the quality-of-life impact (disutility) of an adverse event will be unchanged. It is credible that the cost is higher because the adverse events are more severe, and in this case their impact on health-related quality of life should also be greater. The assumption of independence of parameters lacks face validity. To the extent that parameter values are correlated and modelled as such, the results of OSA will be biased.

The second problem with OSA is that it provides no information on how likely it is that each parameter will take a specific value. Establishing whether there is a possible parameter value that would change the recommendation is useful. However, theoretically possible but highly unlikely values should not carry the same weight in decision making as those that are highly likely. Probabilistic analyses use probability density functions (PDFs) to incorporate the likelihood that a parameter will take each specific value. This is appropriate because not all possible values are equally likely to be the true value. OSA of a probabilistic model throws away this important information that is already included in the model.

2 Probabilistic One-way Sensitivity Analysis (POSA)

While OSA is a flawed approach to meeting the needs of decision makers, the importance of the motivating question remains. It is helpful for decision makers to have insights into the relationship between specific input parameters and the model outputs, particularly the expected costs and outcomes. It is therefore incumbent on analysts to provide as complete and unbiased an answer to this question as possible. What is required is POSA.

POSA requires that (1) the correlation between the value taken by the parameter of interest and other parameters in the model is reflected in the analysis and (2) that the probability of the parameter taking a specific value (the uncertainty about the true value of the parameter) is promulgated through the model and reflected in the outputs from the analysis. Both of these objectives are achieved by running a variation of the analyses required for the conventional (two-step) methods for calculating the EVPPI [5]. In conventional EVPPI, two random samples are drawn—the inner loop and the outer loop.

The outer loop covers the range of values in the distribution of the parameter of interest. For each value drawn from the parameter of interest, a full PSA is run on all other parameters in the model, i.e. a Monte Carlo simulation is run for the same number of simulations as used for the base-case analysis. This is referred to as the inner loop. The results of this inner loop are recorded and then a second value is drawn from the distribution for the parameter of interest and the inner loop PSA is repeated. For our purposes, we do not need to randomly sample the values that form the outer loop, as is conventionally done for EVPPI. Instead, we can systematically select the set of values to form the outer loop that cover the range described by the PDF of the parameter. In choosing the number of values forming the outer loop, there is a trade-off between computational efficiency and precision. For example, analysts may only wish to run inner loops corresponding to centiles or deciles of the distribution, rather than randomly selecting thousands of values from the distribution as would be done in a conventional EVPPI analysis. For illustration, Fig. 2 shows deciles. For each value of the distribution, we report the conditional expected incremental net monetary benefit (cINMB). cINMB is conditional on the parameter of interest, and expected because it is a mean result. This allows for determination of the probability that the cINMB is positive, given the uncertainty in the parameter of interest. The number of values chosen to form the outer loop is a decision regarding the desired precision in characterising the relationship between the value of the specific parameter and cost effectiveness. An example of pseudocode for POSA for an economic evaluation of two interventions is included in an Appendix.

3 ‘Conditional Expected Net Benefit’ and POSA

For each possible value of the parameter of interest, the above analysis provides the expected costs and outcomes for each technology being compared. For the purpose of a POSA, we wish to provide the decision maker with insight into the cost effectiveness of the technology for each possible value and the probability that the parameter takes a value that would change the decision indicated by the central estimate of the reference case analysis.

The limitations with ICERs as a summary measure of a CEA have been well-described elsewhere [6]. One limitation that is particularly pertinent to the construction of tornado diagrams is the behaviour of ICERs when the denominator (incremental quality-adjusted life-years [QALYs]) moves from a negative to a positive value. When this occurs, the ICER flips from a negative to a positive value. As the incremental effect approaches zero, the ICER moves towards infinity. It is impossible to plot these outputs of a OSA using ICERs on a tornado diagram. Therefore, we recommend that the results of POSAs are plotted in the incremental NB space.

The first step in constructing the graphical representation of the POSA is to rank the expected costs and outcomes by the sampled value from the parameter of interest, over the range of values considered in the outer loop. In our example, this is from the 1st to the 99th centile.

Step two is to use the ‘reference case’ value of lambda (the cost-effectiveness threshold) to calculate the cINMB for each value of the parameter.

Step three is to read off, from the PDF, the probability of observing values within each centile of the parameter’s distribution. This information can be used to plot a tornado diagram where the bar plots the credible range for the cINMB between, for example, the 1st and 99th centile of the parameter distribution. The probability of observing a value that produces a positive or negative cINMB can be captured by recording the proportion of the parameter distribution that lies either side of the parameter value at which the cINMB is equal to zero.

An alternative way of presenting the same information is to plot a line graph of the cINMB against the centiles of the parameter distribution. This approach allows the decision maker to read off the probability that the parameter takes a value that is associated with either a positive or negative INMB. In addition, such line graphs allow the decision maker to observe whether the relationship between the parameter and INMB is positive or negative.

4 Example of POSA

As an example, we undertake POSA from a previously published CEA examining the cost effectiveness of Oncotype DX and Prosigna genetic testing in early-stage breast cancer [7]. The study compared the costs and outcomes of alternative prognostic tests used to guide chemotherapy treatment in the management of early breast cancer, where Oncotype DX and Prosigna provide a test result that informs whether a patient is at low, intermediate or high risk (HR) of distant recurrence (DR) in the future. Here, we conduct POSA for three variables: the probability of being offered chemotherapy following a low-risk Oncotype test result, the probability of being offered chemotherapy following a HR Prosigna test result, and the relative risk (RR) reduction in the 9-year probability of DR following chemotherapy.

The distributions for each parameter are described in Table 1.

Table 1 Parameter distributions
Full size table

The data required for the POSA were extracted from a Monte Carlo EVPPI dataset for 99 outer loops for each centile of the parameter in question and 15,000 inner loops. We used these data to estimate the conditional expected costs and outcomes for Oncotype DX and Prosigna. We assumed a cost-effectiveness threshold of $20,000 per QALY and used this to calculate the cINMB for each sampled parameter value. This process was repeated for all three parameters.

For each parameter, the conditional expected costs and outcome data for each centile were obtained. Through this process, we constructed a dataset consisting of the parameter centile value, the probability that the value would be observed, and the cINMB. With these data, the analyst can describe the expected INMB conditional upon the parameter taking that value, and the probability that the parameter will take that value.

Figure 1 is a tornado diagram showing the impact of increasing and decreasing each of the three parameters by 25% on the ICER. For the parameter describing the probability of receiving chemotherapy following a HR Prosigna test result, we can see it is possible for the ICER to go negative. However, whether this leads to a change in the conclusion about which test is cost effective remains unclear. For the probability of receiving chemotherapy following a low-risk Oncotype test result and the RR reduction in the probability of DR following chemotherapy, their ICERs cover a relatively narrow range of positive values. It should be noted that the tornado diagram shown in this way does not provide information on how likely it is that any specific value within that range ± 25% for each parameter will be observed.

Fig. 1
figure 1

Deterministic one-way sensitivity analysis—tornado diagram

Full size image

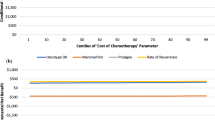
Figure 2 is a line graph plotting the cINMB for each parameter against its probability distribution. For ease, we have only plotted the cINMB for the 1st and 99th centiles as well as deciles 1–9 (i.e. 0.1–0.9), but the graph could be constructed with centiles or even smaller probability increments. Examining Fig. 2, we can see that, when taking into consideration the probability that a parameter will take a value, the results are very different to those in Fig. 1. For example, in the case of the ‘probability of chemotherapy following a HR Prosigna test result’, the probability that the parameter takes a value that leads to a negative cINMB is < 10%. This illustrates how a tornado diagram bar graph cannot be treated as a reliable indicator of the probability of specific values being observed.

Fig. 2
figure 2

Line graph probabilistic one-way sensitivity analysis

Full size image

5 Discussion

Decision makers have always been interested in the impact of specific parameters on the expected value of new technologies [8, 9]. Historically, OSAs have been presented to help decision makers understand this.

However, over the last decade, deterministic CEA has been increasingly recognised as flawed, and a general consensus has emerged around the importance of probabilistic analyses to provide decision makers with unbiased results. Probabilistic models have also become more prevalent, as they provide support to decision makers who wish to use more nuanced decision options such as ‘risk-based patient access schemes’, ‘only in research’ or ‘only with research’ [10].

These developments in the methods and process of health technology assessment have not reduced the importance to decision makers of understanding the impact of specific parameters on expected value. Hence, analysts have continued to provide decision makers with deterministic OSAs, despite the recognition of its methodologic flaws. The continued use of deterministic OSAs represents a retrograde step in the methodological quality of CEA provided to decision makers and has largely continued because of the lack of a methodologically and robust computationally efficient alternative.

The importance of individual parameters in stochastic CEA has conventionally been characterised using the EVPPI. However, EVPPI addresses the question, ‘What would be the value of eliminating uncertainty about the true value of the parameter?’ This is a different question from, ‘What is the probability that this parameter would take a value that changes the decision?’ As we have described, there is a substantial overlap in the analysis required to answer these questions. The primary difference is in the computational burden. POSA requires a much more limited set of outer loops compared with the thousands typically required for EVPPI. In addition, for POSA, the expected costs and outcomes for each outer loop set of simulations are captured, along with the sampled value of the parameter (e.g. centile), and these are linked to the probability that the parameter takes that value (which can be read off the PDF for the parameter used in the probabilistic analysis).

The correct estimate of the credible range for the cINMB and the probability that the parameter will take a value that will change the decision can both be presented to the decision makers using a line diagram that plots the cumulative probability of the parameter against cINMB.

In the same way that probabilistic analyses were initially resisted on the grounds of excessive computational burden [11], it is likely that some will resist moves to replace the biased deterministic OSA because of the need to undertake two-level simulations to produce the data required for POSA. However, we argue that the number of additional simulations is trivial given the computational power of modern computers. Further, advances in the efficiency of the software available for constructing decision analytic cost-effectiveness models mean that such criticisms are not supported by the evidence. A recently completed benchmark comparison of decision analytic modelling software found that R and MATLAB could run value-of-information analyses for a typical model (with 10,000 simulations) in < 1 min using a standard desktop computer [12]. The use of appropriate software means that the production of POSA can be accomplished in similar time periods to those required for probabilistic analyses when it was initially advocated at the start of this century by organisations such as the UK National Institute of Clinical Excellence [2].

As with all developments in the presentation of analytic results to decision makers, care will be required to ensure that decision makers understand the information provided to them. For the tornado diagram, it will be important that decision makers are aware that the bar only shows the credible range for the conditional incremental NB and not the underlying probability of observing a value that changes the recommendation (by flipping the expected net monetary benefit from positive to negative, or vice versa). This additional information can be provided through a line graph that plots cumulative probability against the cINMB.

In the case of reporting the results for more than two interventions, it is necessary to show which intervention is cost effective at each parameter value. In this case, the line for each parameter in Fig. 1 would be modified to show the intervention with the highest net monetary benefit at each centile, which would be analogous to the cost-effectiveness frontier used to report the results from PSAs when there are more than two interventions.

6 Conclusion

Decision makers are interested in the impact of specific parameters on the expected value of new technologies. Probabilistic models are increasingly the norm in CEA, and an efficient and accessible method for POSA is required. POSA is a method with modest computational burden and provides a simple and accessible graphical presentation of its outputs. Application of the method will provide decision makers with unbiased information on how the expected NB is affected by a parameter taking on a specific value and the probability that the specific value will be observed.