Is EQ-5D-5L Better Than EQ-5D-3L? A Head-to-Head Comparison of Descriptive Systems and Value Sets from Seven Countries

Abstract

Objective

This study describes the first empirical head-to-head comparison of EQ-5D-3L (3L) and EQ-5D-5L (5L) value sets for multiple countries.

Methods

A large multinational dataset, including 3L and 5L data for eight patient groups and a student cohort, was used to compare 3L versus 5L value sets for Canada, China, England/UK (5L/3L, respectively), Japan, The Netherlands, South Korea and Spain. We used distributional analyses and two methods exploring discriminatory power: relative efficiency as assessed by the F statistic, and an area under the curve for the receiver-operating characteristics approach. Differences in outcomes were explored by separating descriptive system effects from valuation effects, and by exploring distributional location effects.

Results

In terms of distributional evenness, efficiency of scale use and the face validity of the resulting distributions, 5L was superior, leading to an increase in sensitivity and precision in health status measurement. When compared with 5L, 3L systematically overestimated health problems and consequently underestimated utilities. This led to bias, i.e. over- or underestimations of discriminatory power.

Conclusion

We conclude that 5L provides more precise measurement at individual and group levels, both in terms of descriptive system data and utilities. The increased sensitivity and precision of 5L is likely to be generalisable to longitudinal studies, such as in intervention designs. Hence, we recommend the use of the 5L across applications, including economic evaluation, clinical and public health studies. The evaluative framework proved to be useful in assessing preference-based instruments and might be useful for future work in the development of descriptive systems or health classifications.

Introduction

Since the introduction of the original EQ-5D descriptive system in 1990 [1] and the first value set in 1997 [2], the EuroQol Group has continuously furthered research aimed at enhancing the instrument [3, 4]. This entailed refining the descriptive system, developing new valuation methodology and also developing new EQ-5D instruments for specific use. Examples of the latter include the child-friendly EQ-5D version (EQ-5D-Y) as a more comprehensible instrument suitable for children and adolescents [5, 6], and the exploration of EQ-5D versions with one or two additional dimensions to the descriptive system [7,8,9,10]. Arguably, the biggest change has been in refining the ‘granularity’ of the five dimensions by replacing the three response options (levels) of the original EQ-5D (now ‘EQ-5D-3L’) with five levels. The official EQ-5D-5L descriptive system (for convenience we use the term ‘5L’ from here) has been available since 2011 [11] and is currently available in more than 150 translations and multiple modes of administration [12]. In parallel, a new valuation protocol for the 5L was developed (EQ-VT) to establish new country-specific value sets, warranting a high level of standardisation and quality control as well as introducing new and improved valuation methods [13, 14].

Several studies have compared the descriptive systems of EQ-5D-3L (for convenience we use the term ‘3L’ from here) and 5L in terms of their measurement properties, including distributional characteristics such as ceiling effects and evenness, reliability and various types of validity [15,16,17,18,19,20,21,22]. Most studies showed that the 5L descriptive system had better or at least similar measurement properties compared with 3L, but two remarks apply. First, we must establish whether the increased descriptive richness of 5L will increase measurement precision rather than measurement error, as this a trade-off. Further, considering that the EQ-5D is a preference-based instrument, it is essential also to investigate whether the increased descriptive richness translates into increased sensitivity of its utility-based index values (hereafter ‘utility values’ or ‘utilities’); again, error may increase due to the increased difficulty in valuing more refined health states. The final question is whether the combined descriptive and valuation effects of 5L improve the discriminatory potential of the utility instrument in, for example, the estimation of quality-adjusted life-years (QALYs) in economic evaluation. As the measurement of health status with the descriptive system is independent from the derivation of utility values and involves different methodologies, improved sensitivity and discrimination of the descriptive system does not necessarily translate into better discriminatory power using utilities (comparing groups or comparing pre- and post-intervention health state). For economic evaluation (e.g. cost-utility analysis), improved discriminatory performance of the utility values would represent a major advantage.

To compare the performance of 3L and 5L in terms of QALYs gained, longitudinal patient-level data on both 3L and 5L in one or multiple study populations would be preferred. In the absence of such longitudinal data we compared 3L and 5L using data from a large multi-country cross-sectional survey, applying country-specific value sets for seven countries.

We first compared the distributional characteristics of the observed utility values by value set, and standard descriptive statistics by condition group and value set. Our main analysis consisted of two tests of discriminatory power. In order to further clarify and explain the results, we performed an exploratory analysis to determine the factors responsible for certain patterns in the results. In this analysis, a clear distinction was made between differences caused by descriptive system results and by the utility values applied to the descriptive data. The separation of descriptive and valuation effects has proven to be of use in an earlier study exploring differences in utilities derived from different preference-based instruments [23]. We introduce an evaluative framework consisting of a novel combination of non-parametric methods to establish increased measurement refinement (if any), with parametric methods to demonstrate improved discrimination (if any); 5L is only better than (rather than ‘different from’) 3L if (1) more response levels are efficiently used without a decrease of uniformity of the distribution and (2) this increased use is not offset by more measurement error, both in terms of description and valuation.

Our study had two research questions: (1) Do 5L value sets perform better than 3L value sets in terms of discriminatory power, as a direct result of the improved descriptive sensitivity? (2) What are the underlying factors affecting this performance? Our approach allowed us to make normative assessments on the performance of both instruments and to offer recommendations to users of EQ-5D instruments.

Methods

Paired EQ-5D-3L–EQ-5D-5L (3L–5L) Descriptive Data

A large multinational dataset that included paired descriptive 3L and 5L data for eight patient groups and a student cohort was used [15, 24]. These data were obtained with the standard 3L and 5L versions for self-report use in adults, describing health on the dimensions of mobility, self-care, usual activities, pain/discomfort and anxiety/depression. The 3L version applied the level descriptors (or labels) ‘no problems’, ‘some/moderate problems’ and ‘extreme problems/unable to’, and the 5L version used ‘no problems’, ‘slight problems’, ‘moderate problems’, ‘severe problems’ and ‘extreme problems/unable to’. For mobility, the most severe response option was changed from ‘confined to bed’ for 3L to ‘unable to walk about’ for 5L. The 3L classification describes 243 unique health states (or health profiles) that are often reported as vectors ranging from 11111 (full health) to 33333 (worst health), whereas the 5L defines 3125 unique health states, with 55555 as the worst health state.

Paper-and-pencil versions of the questionnaires were used in all countries except in England where data collection took place online. Since there were many condition-specific subgroups with small sample sizes, it was decided to combine related patient groups, resulting in nine main condition groups. Only respondents who completed both the 3L and 5L¹ without any missing responses were included in the analyses (a 3L–5L comparison of missing values is reported elsewhere [15]). It was assumed that within a specific condition group country differences were not important so that descriptive data could be pooled.

Paired 3L–5L Value Sets

At the time of this study there were seven countries with both 3L and 5L value sets available, namely Canada, China, England/UK (5L/3L, respectively), Japan, The Netherlands, South Korea and Spain [2, 25,26,27,28,29,30,31,32,33,34,35,36,37]. All EQ-5D value sets were obtained using representative samples of the general public, ensuring that they represented the societal perspective. A value set is a set of weights that can convert each health state into an index value on a scale anchored at 1 (referring to full health) and 0 (referring to a state as bad as being dead), allowing for negative values for health states considered to be worse than dead. Most 3L valuation studies followed similar protocols, although there were notable differences with regard to the sampling of respondents (affecting representation), sample size and health state design (varying from 17 to 101 valued health states) [38, 39]. All 3L valuation studies were performed with face-to-face interviews and paper-and-pencil methods except for Canada where a web survey was used. All 3L value sets were based on time trade-off (TTO) data. With the introduction of 5L a standardised valuation protocol was developed, the EQ-VT (EuroQol Valuation Technology Platform) [13]. In addition to standardisation in terms of health state design, valuation methodology and a computer-assisted personal interview mode of administration, a strict protocol of interviewer training and quality control during the entirety of the data collection process was developed and implemented [14]. Discrete choice experiment (DCE) methodology was introduced in the EQ-VT, along with composite TTO as the main valuation method. Since there is no standardised analytic protocol, some 5L value sets were based on hybrid models utilising both TTO and DCE data while others were based on TTO data only. After the initial valuation studies were performed using EQ-VT version 1.0 (Canada, China, England, The Netherlands, Spain) some data quality issues and interviewer effects were apparent and a cyclic quality control process was introduced in version 1.1, which led to a substantial improvement [14].

Usually country-specific utility values are used to conduct analyses in a population or patient sample from that particular country, reflecting the appropriate preferences. Since our research questions were of a methodological nature, aiming at making generalisations across value set characteristics, we used the pooled multi-country dataset to compare the characteristics of 14 country-specific 3L and 5L value sets.

Analyses

3L and 5L Value Sets for Seven Countries

Characteristics of all value sets were reported in terms of model parameters and model characteristics, such as the modelled value range, intercept, interaction parameters and histograms of all possible values (3L: 243; 5L: 3125), which may be responsible for differences in performance between 3L and 5L (see Table 1).

Table 1 Characteristics of EQ-5D-3L and EQ-5D-5L value sets from seven countries

Distributional Analyses of 3L and 5L Utility Values

Country-specific 3L and 5L utility values were calculated for each value set for all condition groups combined and described numerically and graphically using histograms. We examined clusters and discontinuities (‘gaps’) in the histograms as such patterns theoretically diminish the sensitivity and the accuracy of the instruments and might lead to estimation problems [40].

In order to assess the frequency and efficiency of use of the utility scale we applied Shannon’s indices as a means of assessing distributional evenness [17, 18, 21, 22]. While Shannon’s H′ captures absolute informativity and is simultaneously powered by evenness and the number of categories used, Shannon’s J’ index of relative informativity solely reflects the evenness of a distribution [41]. Since Shannon’s J′ corrects for the total number of possible categories (here: possible utility values), which could be potentially close (or equal) to 243 for 3L and 3125 for 5L, it was not considered to be a fair comparison (we expected that J′ would result in higher values for 3L for this reason). Hence, we also calculated both indices by subdividing the scale range in categories (‘bins’) with a width of 0.05, making the number of categories between 3L and 5L more comparable.

Subsequently, we presented mean utility values (and standard deviations [SDs]) by condition group for all 14 value sets, with the addition of an equal weighting score (Level Sum Score [LSS] transformed to a 0–1 scale) in order to assess the impact of the descriptive data without the effect of utility weights. The transformed LSS (tLSS) was calculated by summing the level scores for the five dimensions and performing a linear transformation on this sum score to a 0–1 scale so that the value for 11111 is equal to 1.0 and 33333 (for 3L) or 55555 (for 5L) is equal to 0.

Discriminatory Performance of 5L Versus 3L

Two tests of discriminatory power were conducted, accommodating different distributional assumptions with respect to utility values: one based on the F statistic (parametric), the second on receiver-operating characteristics (non-parametric).

Discriminatory power was assessed using the F statistic derived from analysis of variance (ANOVA) to test the equality of means. The F statistic is widely used to assess the relative efficiency of patient-reported outcome measures [21, 42, 43] and is based on differences in group means divided by the standard error of the difference. A higher F statistic means a higher likelihood for a measure to show statistical significance when used to compare groups. Hence, higher F statistic values indicate higher discriminatory power. To express the discriminatory power of 5L relative to 3L we computed the ratio of their F statistics resulting from comparisons of different condition groups, in such a way that a ratio higher than 1.0 indicated that 5L was more discriminative than 3L: relative efficiency = F statistic_5L/F statistic_3L.

Comparisons were made between (1) the eight disease groups and the student cohort, assuming the students were a valid proxy for a healthy population sample; and (2) patients with a mild condition versus those with a moderate or severe condition. Using the observed mean EQ-5D visual analogue scale (EQ VAS) ratings as reference, we defined diabetes and liver disease as mild conditions (relative to the other conditions), and the remaining six as moderate to severe conditions. Since our main aim was to compare measurement properties of 3L and 5L, we considered this method to be suitable for assessing their ability to distinguish between mild and moderate/severe condition groups.

As a second analysis, we calculated the area under the receiver-operating characteristics curve (AUROC) as a non-parametric method of assessing discriminatory power. AUROC analyses were performed for each pair of condition group comparisons using pooled data on the groups, with group membership being the outcome and the 3L/5L utility score being the exposure. AUROCs for 3L and 5L were calculated and the ratio (5L/3L) was used as the measure of discriminatory power. The AUROC value can range from 0.5 (no prediction) to 1.0 (perfect prediction). Consequently, a 5L/3L AUROC ratio > 1.0 indicates 5L to be more discriminative than 3L. While the F statistic is directly based on means and dispersion, the AUROC employs the full distribution.

For all comparisons 95% confidence intervals (CIs) of the F statistic and AUROC ratios were calculated using 3000 bootstrap samples, enabling us to test whether the ratio was statistically different from 1.0.

Exploration of Factors Affecting Discriminatory Power

At least three separate factors determine discriminatory power results:

• 1. The effects of the descriptive system, involving choice of dimensions, number of levels and corresponding labels, translation effects and reporting heterogeneity.

• 2. Valuation effects, relating to the valuation protocol, the valuation study (interviewer effects, quality control, etc.) but also to the modelling of the valuation data. Valuation effects also encompass true country-specific variation in preferences, which may be caused by many underlying factors, e.g. cultural, geographical or related to demographics, language or health system.

• 3. A third factor is related to the ability of any scale to capture the location of a respondent on the true latent scale. The precision of measuring this location will have an impact on the descriptive data and consequently the utility distribution of any study sample. As it appears this important factor is often ignored, we discuss this in some detail.

A graphical example can illustrate potential misclassification effects due to distributional descriptive 3L–5L effects (Fig. 1). The general methodology has been widely discussed in research on reporting heterogeneity [44,45,46,47,48]. Imagine a health dimension scaled with three levels of granularity: 3L, 5L and 10L (3, 5 and 10 levels respectively). In this example we do not take specific labels into account (although ‘1’ refers to no problems). There is an underlying unobservable latent scale which is assumed to be continuous: all three measurement systems (3L, 5L, 10L) will only be approximations of the true latent value. The transition area of two adjacent categories is called the cut-off point (or ‘cut-point’), and in the development of measurement scales one strives for clearly defined cut-points with little overlap (as defined by the labels), to avoid error. The distribution of observed scores of the 3L, 5L and 10L ordinal scales depends on the cut-points. Random error may occur at the cut-points when overlap exists, and this overlap may differ between 3L, 5L and 10L. Note that random error may cause a shift of average values for the extreme categories of the scale, as misclassification can only be towards the middle level of the scale due to the censored nature of the EQ-5D dimensions. Also note that when applying labels, the middle category of 3L does not necessarily coincide with the middle level of 10L, or would have the same latent midpoint, i.e. the middle point of the category, equidistant from both cut-points. Various types of misclassification may occur between the three systems. Imagine five different locations on the latent scale (A through to E), which we here refer to as respondents, although these also might indicate group averages. For respondent A there is no discrepancy between 3L, 5L and 10L: no problems are scored in all three systems. For respondent B both 3L and 5L lack refinement (no problems) as evidently there are reported problems on 10L. Respondent C illustrates the reduced ceiling effect with the introduction of 5L over 3L: no problems are reported in 3L whereas problems are reported on 5L. Respondent D might contribute to an overestimation of reported health problems in 3L when compared to 5L: the middle 3L category is chosen whereas a milder category is chosen for 5L. The distance from the 3L midpoint to the true latent value (X) is larger than the distance from the 5L midpoint to the latent value (Y) and smallest with 10L (Z). The same goes for respondent E: the most extreme category is chosen for 3L whereas a less severe category is scored on 5L. As mentioned, these location effects may also apply to group means, potentially leading to misclassification, especially when the group is rather homogeneous. Random error will increase if the mass of observations of a group is close to a cut-point of the scale such as location D, and may then have a strong impact on a crude scale such as 3L, but may only have a small effect on a more refined scale such as 5L, and even less on 10L. Generally, we assume that more levels theoretically will lead to less measurement bias.

Fig. 1

Illustration of location effects when five hypothetical latent health states (A through E) are measured on three scales with varying levels of granularity (3L, 5L, 10L). 3L 3 levels, 5L 5 levels, 10L 10 levels

With regard to factor 2, specific modelling outcomes on the intercept and dimension coefficients and the use of interaction terms such as the N3 term (representing whether any dimension is at level 3) will affect the resulting utility distributions and may subsequently affect discriminatory power. To explore the role of these modelling effects we studied the impact of altering the models (based on the original valuation data) by performing a sensitivity analysis in which we excluded the N3 term for two 3L value sets (The Netherlands, UK).

We explored the role of factors 1–3 both numerically and graphically. The point of departure was the LSS of the descriptive data, both by dimension and summed over all dimensions. From the LSS, difference scores between 3L and 5L were calculated by condition. We investigated how various value set characteristics contributed to discriminatory power results using tLSS (LSS transformed to a 0–1 scale) as a reference.

As a way of disentangling the intertwined effects of various factors affecting discriminatory power, we performed a multiple regression analysis with the F statistic and AUROC as dependent variables and the following variables representing value set or descriptive system characteristics as independent variables: intercept (continuous), modelled range (continuous), N3 (continuous, we included only N3 since this was the most prominent interaction term), version (with 3L as reference) and country (with Canada as reference).

Results

3L and 5L Value Sets for Seven Countries

There were substantial differences in the models across value sets (Table 1). For most countries the modelled 5L value range was smaller than that for the 3L, with the exception of China and The Netherlands. If 5L value sets included an intercept, its size was much smaller than 3L (except for South Korea where the intercept was 0.050 for 3L and 0.096 for 5L). The ‘upper gap’ between the value for 11111 and the second best health state was reduced quite substantially in 5L, ranging from a 0.02 reduction for The Netherlands and 0.04 for Spain to 0.09 for Japan and 0.14 for Canada, with South Korea as the exception (0.09 for 3L and 0.12 for 5L). Note that for Canada the upper gap was only 0.02 for 5L, because the value for 11111 was set at 0.949 (1 minus the intercept). Five countries included the N3 term in their 3L model, while for 5L only two countries used a similar interaction term (Canada and South Korea). Considerable variation was apparent in the model coefficients indicating the utility value decrement (‘disutility’) of dimensions, with mobility showing the highest decrements for level 3 (3L) for Canada, China, Japan, South Korea and Spain and for level 5 (5L) for China, Japan and South Korea. Pain/discomfort had the highest decrement for level 3 (3L) for the UK and The Netherlands and for level 5 (5L) for Canada, England and Spain. Anxiety/depression showed the second largest disutility in 5L for Canada, England, Japan and Spain and the largest for The Netherlands. For The Netherlands, both 3L and 5L value sets include large disutility values for anxiety/depression.

Figure 9 (Appendix) depicts the distribution plots for all possible values for the 3L and 5L value sets. Note that these plots are ranked by utility value for 3L and 5L separately, implying that ‘comparable’ health states such as 21111 for 3L and 31111 for 5L can be at different positions on the common utility space (X-axis). For England/UK and Spain, most 3L index values were concentrated at a much lower segment of the utility scale when compared to 5L, while for China it was vice versa, although to a lesser extent.

Distributional Analyses of 3L and 5L Utility Values

The descriptive final dataset consisted of 3L and 5L health profile data for 3467 respondents, with the smallest and largest condition groups being depression (n = 250) and liver disease (n = 588), respectively (Table 2). The ceiling was always lower in 5L, ranging from a difference between 3L and 5L of 0.8% (stroke) to 12.7% (students). Floor effects were negligible.

Table 2 Characteristics of descriptive EQ-5D data for nine condition groups

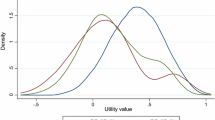
Figure 2 depicts the empirically observed utility values for all countries. The 5L distributions are smoother and more evenly distributed than those for 3L. The 3L value distributions often show clusters and discontinuities across the entire range of the scale. Due to the intercept for 3L there is a large upper gap for Japan and Canada, and to a slightly lesser extent for The Netherlands and the UK. The 5L country-specific distributions look rather similar despite the model heterogeneity, although for South Korea and Japan the effect of the intercept is also clearly visible. While for England and Spain most possible 3L utility values (Fig. 9, Appendix) were concentrated at a much lower segment of the scale than 5L, the observed values did not show this pattern.

Fig. 2

Histograms of observed utility values based on value sets from seven countries, all condition groups combined. 3L EQ-5D-3L, 5L EQ-5D-5L

The non-parametric Shannon’s H′ and J′ indices numerically reflected the graphical results (Table 3). For all comparisons, Shannon’s H′ was much higher for 5L and Shannon’s Evenness J′ index also was consistently higher for 5L. After subdivision into 0.05 utility space categories 5L clearly showed substantially higher values than 3L for both indices in all countries, establishing better distributional evenness for 5L overall.

Table 3 Distributional evenness (Shannon’s indices) of EQ-5D-3L and EQ-5D-5L utility values from seven countries: all condition groups combined

Figure 3 shows the observed country-specific mean utility values for each condition group (means and SDs are listed in Table 6, Appendix). The presentation as a line graph was chosen to facilitate pattern comparison between 3L and 5L. Overall, the same ranking of average utilities per condition group across countries is visible in the figure and also a strong similarity of utilities with tLSS (showing only descriptive 3L–5L differences). Two patterns are visible: between-country valuation effects appeared larger than 3L versus 5L effects (judging from the scale differences between countries), and 3L–5L utility differences did not seem to add very much to the difference based on tLSS between 3L and 5L. For mild conditions 5L SDs were generally smaller, except for England/UK and Spain where SDs in 5L were smaller overall. Two countries displayed close to identical 3L and 5L condition group means (Canada and Japan). The other countries and tLSS values generally indicated an upward or downward shift. The UK showed a universal upward shift of 5L, South Korea a downward shift, the remaining countries (China, The Netherlands and Spain) showed a general shift plus a modifying effect in four conditions: CVD, stroke, asthma/chronic obstructive pulmonary disease (COPD) and rheumatoid arthritis (RA)/arthritis, which may have been caused by location effects.

Fig. 3

Mean 3L and 5L utility value per condition group for seven countries and the transformed Level Sum Score. 3L EQ-5D-3L, 5L EQ-5D-5L, COPD chronic obstructive pulmonary disease, CVD cardiovascular disease, RA rheumatoid arthritis

Discriminatory Performance of 5L Versus 3L

Both 3L and 5L distinguished well between the healthy and the disease groups as well as between mild and moderate/severe condition groups for all country-specific value sets. All comparisons resulted in statistically significant results. However, performance in terms of relative efficiency varied noticeably across version (3L/5L), value set (country and model effects) and the condition groups compared. Generally, 3L performed better in the healthy–disease comparisons while 5L performed better comparing mild and moderate/severe conditions (Fig. 4). Japanese and Dutch 5L value sets performed better overall while Canadian and Chinese 3L value sets performed better overall. The bootstrap analysis showed that although most significant results were quite robust, some were borderline significant while others were borderline non-significant.

Fig. 4

Observed relative efficiency of 5L over 3L using the F statistic ratio. Green cells indicate a significant F ratio showing better discriminatory power for 5L, orange cells for 3L (95% CI, 3000 bootstrap samples). 3L EQ-5D-3L, 5L EQ-5D-5L, CI confidence interval, COPD chronic obstructive pulmonary disease, dis. disease/disorder, RA rheumatoid arthritis, tLSS transformed Level Sum Score

The results for the AUROC analysis generally supported the relative efficiency results (Fig. 5), with 3L showing a better performance in the healthy–disease comparison, and 5L in the mild versus moderate/severe comparisons. However, overall results showed a significantly better performance for 5L over 3L when compared to the relative efficiency results, except for Japan.

Fig. 5

Observed relative efficiency of 5L over 3L using the AUROC. Green cells indicate a significant AUROC comparison showing better discriminatory power for 5L, orange cells for 3L (95% CI, 3000 bootstrap samples). 3L EQ-5D-3L, 5L EQ-5D-5L, auc area under the curve, AUROC area under the receiver-operating characteristics curve, CI confidence interval, COPD chronic obstructive pulmonary disease, dis. disease/disorder, RA rheumatoid arthritis, tLSS transformed Level Sum Score

Exploration of Factors Affecting Discriminatory Power

For the exploratory analysis we initially focused on the descriptive data, comparing LSS by dimension. Table 4 shows a pronounced shift effect between 3L and 5L (LSS by dimension recoded to no problems = 0; 3L on the same scale as 5L). A standardised difference score (Δ) was calculated, adjusting for sample size. For almost all condition groups and all dimensions, a shift to less reported health problems on 5L when compared with 3L occurred, except for mobility, where 5L represents more health problems for five condition groups due to ‘confined to bed’ barely being endorsed in 3L. The sum of the standardised differences scores shows that over all five dimensions the 3L–5L difference (shift) was smallest for the healthy population (28.4) and largest for liver disease (75.0). Level distributions by dimension for the pooled dataset graphically depict this main trend (Fig. 6). The shift was mainly caused by the very large proportion of respondents scoring level 2 on 3L who scored a level 2 or level 3 on 5L (average 85% over dimensions), leaving a very small proportion scoring level 4 on 5L. For pain/discomfort and anxiety/depression this also occurred at the extreme end of the scale, with a larger proportion scoring level 3 on 3L who scored level 4 on 5L rather than level 5. These observations translate into the conclusion that 3L as a scale tended to overestimate health problems when compared with 5L.

Table 4 EQ-5D-3L versus EQ-5D-5L Level Sum Score by dimension^a and condition group, including a standardized level shift indicator (Δ = 3L − 5L adjusted for sample size)^b

Fig. 6

Percentage of reported problems to 3L and 5L descriptive systems: all condition groups combined. 3L EQ-5D-3L, 5L EQ-5D-5L

Overall, 3L resulted in higher relative efficiency ratios for the healthy–disease comparison whereas 5L performed better for the mild versus moderate/severe comparisons. Figure 7 provides an example explaining this trend. Using tLSS as reference, 3L has overall lower average values than 5L, but as mentioned earlier the differences for the healthy population were smallest, while for the other condition groups they were larger, resulting in a larger difference in means between the healthy and disease groups for 3L (X) than for 5L (Y), reflected in higher F statistics for 3L. For the mild disease showing the most pronounced results on relative efficiency (liver disease), the descriptive difference between 3L and 5L was largest (Table 4). Here the difference pattern was reversed, as indicated at the foot of Fig. 7. The difference in means between the mild and moderate/severe diseases was larger for 5L (Y) than for 3L (X), resulting in higher discriminatory power for 5L.

Fig. 7

Observed redistribution of latent health states from 3L to 5L if descriptive refinement increases. 3L EQ-5D-3L, 5L EQ-5D-5L

When exploring 3L–5L differences of the country-specific utilities, various model characteristics emerged as important underlying factors. A large intercept generally results in a lower mean and increased variance around the mean. The net effect on the F statistic is difficult to predict since both the difference of means and the standard error of the difference are affected. Overall, we detected a negative effect on discriminatory power, exemplified by the very large 3L intercept of Japan, leading to inferior performance when compared to 5L. Second, an effect of the use of model interaction terms was visible. The large N3 terms for the UK, Spain (and to a lesser extent for The Netherlands) appeared to negatively influence discriminatory power, caused by a substantial increase in variance. Note particularly that the Canadian 3L set did not contain an N3 term, but the 5L did include an ‘N4 or N5’ term which might have contributed to poorer discriminatory performance of 5L. Partly caused by the N3 term, but also due to other characteristics of 3L value sets, clusters and gaps occurred in the utility distributions, especially in the moderate to severe region (0–0.5), whereas 5L employed the utility scale more efficiently, resulting in smoother distributions. The histograms for the separate condition group comparisons demonstrate that the modelled range of a given value set bore no relation to the F statistic results. Instead, the use of the scale was decisive (as also shown in Fig. 2). One example is liver disease: while the modelled range for 5L in Canada and Japan was much smaller than for 3L, the available value range was being used much more frequently and efficiently in 5L, contributing to higher discriminatory power in 5L.

The sensitivity analysis, exploring the effect of excluding the N3 term for the 3L value sets for the UK and The Netherlands, confirmed this pattern. Discriminatory power clearly increased for 3L as the number of significant results in favour of 3L increased from 3 versus 4 (3L vs. 5L) to 9 versus 2 for the UK and from 1 versus 10 (3L vs. 5L) to 4 versus 5 for The Netherlands (Figs. 4, 8). Descriptive statistics showed that this was mainly due to lower levels of dispersion for the models without N3.

Fig. 8

Sensitivity analysis main effects without N3 for UK and The Netherlands: observed relative efficiency of 5L over 3L using the F statistic ratio. Green cells indicate a significant F ratio showing better discriminatory power for 5L, orange cells for 3L (95% CI, 3000 bootstrap samples). 3L EQ-5D-3L, 5L EQ-5D-5L, CI confidence interval, COPD chronic obstructive pulmonary disease, dis. disease/disorder, N3 any level 3, RA rheumatoid arthritis

The results from the regression on the F statistic were a way to validate our interpretation of the relative impact of various factors. Our findings were confirmed (Table 5), demonstrating a significant negative coefficient for 5L for the healthy–disease comparison and a positive coefficient for the mild versus moderate/severe comparisons. The modelled range was not significant for both types of comparison, confirming that the modelled range did not significantly impact upon the F statistic. The intercept showed a significant negative value for the healthy–disease comparison, implying that the use of an intercept decreases discriminatory power. The N3 term did not show a significant impact. It is of interest to note that the value sets for the Asian countries resulted in higher discriminatory power than for the non-Asian countries. Using the AUROC as the independent variable showed similar patterns, where the intercept consistently showed a negative effect, as did the N3 term for the mild versus moderate/severe comparison. The modelled range, however, appeared to contribute to discriminatory power.

Table 5 Effect of value set characteristics on discriminatory performance in terms of F statistic and area under the receiver-operating characteristics curve

Discussion

Our study showed that the 5L version of the EQ-5D instrument was in many respects superior to the original 3L version. By separating the performance of description and valuation, it became clear that these benefits mainly arise from the improved descriptive system: 5L was superior in terms of the distributional evenness, efficiency of scale use and the face validity of the resulting distributions, leading to an increase in sensitivity and precision in health status measurement. Refinement of 5L was not offset by more error, neither in terms of description nor in valuation.

The fewer cut-points of 3L (two instead of four in 5L) and the position of the cut-points relative to the true latent scale position could be the main drivers of the larger error component in 3L. The net effect was that 3L overestimated self-reported health problems by displaying ‘moderate problems’ where the true latent score most often was more likely to be in between ‘no problems’ and ‘moderate’, i.e. 3L suffered from a rather high cut-point between levels 1 and 2 (and for pain/discomfort and anxiety/depression also between levels 2 and 3). The impact of this artefact of the descriptive system decreased when the number of levels increased. The fact that 3L systematically overestimated reported health problems was unexpected, as for certain condition groups (e.g. in severe patients) the level of reported health problems between 3L and 5L could have been similar, or 3L could have led to the reverse finding. i.e. an underestimation of health problems. The overestimation of 3L was not trivial and affected any difference score when making comparisons: differences may be underestimated or overestimated, such as the overestimation of the difference between a healthy population and most patient groups in our study. This disadvantage of 3L has further consequences in the valuation procedure: if respondents were to value a 3L health profile with moderate problems, and no information was available to inform them that this would actually (empirically) refer to a mix of moderate and predominantly milder health problems, then the disutility would also be overestimated.

When adding utility values to the descriptive data, it was apparent that although absolute utility means varied substantially, 3L–5L differences were not very large, as usually a constant upward or downward shift was observed. Nevertheless, this study showed that seemingly small differences do affect results in discriminating between groups, and are likely to also affect responsiveness. A more precise discrimination between subgroups is achieved with 5L. The effect on QALY comparisons might be smaller since here it would mainly be the difference of mean utilities that would determine the outcome, with the exception being heterogeneous diseases and/or populations where the redistribution effects were non-linear (in our study CVD, stroke, asthma/COPD and RA/arthritis), where larger differences might be expected.

On the assumption that the increased number of levels in 5L led to less bias in the resulting utilities, we concluded that 3L overestimated health problems and consequently underestimated utilities when compared with 5L. This was generally observed across condition groups, but was most pronounced in liver disease (caused by a large misclassification at location D, as depicted in Fig. 1). Against our expectation, health problems in this group were apparently very mild [49], as confirmed by the high mean EQ VAS rating. A result of 3L misclassification is a biased assessment of discriminatory power that could lead to an overestimation of discriminatory power of 3L in the healthy versus disease comparisons in our study, or an underestimation of discriminatory power in the mild versus moderate/severe comparisons.

For mild conditions SDs were lower in 5L, which may be a consequence of 3L overestimation being larger in these conditions, as 5L was better equipped to capture the (very) mild skewed distribution, resulting in lower SDs. For moderate and severe condition groups, 5L SD rates were higher. Graphical and numerical (Shannon’s indices) evidence clearly showed that 5L covered a much wider range of the utility scale in these condition groups and was more evenly distributed, which in our view resulted in a much better reflection of the true underlying distribution. Note also that for the UK and Spain, 3L levels of dispersion were higher overall, which was in part due to the inclusion of the N3 term.

The analysis additionally proved useful in detecting inter-country differences. The relatively poor performance of 5L in some countries may relate to the use of the initial EQ-VT version 1.0. For instance, in Canada and England very few negative values were derived, which could be caused by poor protocol compliance of the interviewers and/or a poor explanation of the worse than dead task in the composite TTO exercise. In general, the value sets for the Asian countries showed better discriminatory power than non-Asian countries. We must also accept that structural components influence preferences, with many possible underlying factors involved (e.g. culture, demographics, language, geography), which was also noted by Olsen et al. [50].

Our study rested on two unique features:

• 1. The development of an innovative framework to assess the performance of preference-based measures of health with varying levels of sensitivity. Note that a framework such as the COSMIN (COnsensus-based Standards for the selection of health Measurement Instruments) taxonomy only partially applies to instruments with separate descriptive and valuation components [51, 52].

• 2. The use of a large number of published value sets ‘as is’ in a large multinational parallel 3L–5L dataset across nine condition groups.

Our innovative framework started with the separation of potential systematic effects in description and valuation. This enabled us to clarify hitherto poorly understood mechanisms underlying differences with a 3L versus a 5L system [19, 53]. Our study confirms some of the findings from an earlier study by Richardson et al. [23], showing that differences between utility results of different preference-based instruments are mainly attributable to the descriptive data, although a different methodological approach was followed in their study, based on parametric techniques. Our framework incorporated ceiling and floor effects, and Shannon’s indices as expressions of the evenness of a distribution. Distributional characteristics were based on the straightforward assumption that we should expect normal or lognormal distributed outcomes, as commonly observed in many naturally occurring phenomena, including self-reported health [54,55,56]. We improved on the use of the F ratio to quantify discriminatory power, differentiating between the various underlying sources, e.g. random error, cut-point-related bias and dispersion in heterogeneous samples. The successful use of the AUROC is an example of the wide applicability of this method beyond diagnostics. This study shows only part of its potential, as described elsewhere [57, 58]. A main advantage of our framework lies in the combined strength of the distributional approaches and different methods to assess discriminatory power, enabling us to make claims of the superiority of one measure over another. Our methods make clear that 5L is better than 3L, but they could also demonstrate that a hypothetical 10L might be a poor choice.

There were some limitations that must be acknowledged for the current study. First, the condition samples were not optimal for all groups. We used a student cohort to represent a healthy population, whereas a better matched general population sample, especially in terms of age and education, would have been more suitable. Second, we cannot exclude the possibility that inter-country differences in the descriptive data existed. The condition groups were from various countries, e.g. the liver disease sample was derived from an Italian cohort, the student cohort was entirely Polish and the personality disorder sample was Dutch. The F statistic was a key component of our study, assuming a normal distribution. The 3L and 5L utility scores used in our study were often not normally distributed due to ceiling effects or clusters, although in the context of health measurement the key factors are similarity of the distributions rather than normality, and approximately equal-sized samples [42]. Our conclusion that 3L overestimated health problems might be challenged for the first three dimensions where level 2 of 3L (some problems) was not identical to level 3 of 5L (moderate problems), although we felt justified generalising over all five dimensions since for pain/discomfort and anxiety/depression, where all labels are identical, overestimation was largest. Finally, as our study was based on cross-sectional data, we cannot make firm conclusions about the 3L versus 5L impact on QALYs. However, in the main pharmacoeconomic application of EQ-5D (cost-utility analysis), the utilities for different health states that are modelled are typically based on cross-sectional data, often derived from different patients subgroups.

Conclusions

Our study has several implications. Although the 3L can be considered to be a valid measure in itself, we demonstrated that its lack of refinement did lead to more reported health problems on average when compared to a more sensitive and precise measure. We are aware that an even more refined system might reveal misclassification in 5L, but these effects will on average be much smaller. We conclude that 5L results in more precise and valid outcomes, both descriptive and in terms of valuation. The increased sensitivity and precision of 5L is likely to be generalisable to longitudinal designs, such as intervention studies. Hence, we recommend the use of 5L across applications, including economic evaluation, clinical studies and burden of disease or public health studies (e.g. for establishing population norms). Our results indicate that in situations where patient groups would experience a uniform recovery to nearly full health, 3L might artificially show a large effect. This might have led to the overestimation of QALY gains in past economic evaluations, especially in assessing the impact of drugs for mild diseases.

With regard to modelling of the utility data, it was apparent that the inclusion of an interaction term (such as N3) and an intercept would lead to undesirable distributional characteristics such as discontinuities and clusters in the utility scale and would be likely to reduce discriminatory power. It is notable that for the two countries that included an interaction term in their 5L model (Canada and South Korea), discriminatory power was not outstanding. Note that a large intercept might have been caused by misspecification of mild health states in the valuation procedure (by assigning low utility values), which could be due to interviewer effects (especially apparent in EQ-VT version 1.0) or cognitive overload in respondents. Our finding that the use of the scale was an important determinant of discriminatory performance (as opposed to the modelled range) shows that the previous preoccupation with the modelled range is not really justified [29, 50], which was also reflected in our regression results (Table 5). The use of 3L in conditions with problems with mobility could lead to severe underreporting of mobility problems. In our study COPD or CVD patients showed many reported problems in walking about on 5L, but since these respondents were not confined to bed they were restricted to score level 2 on 3L, thereby reducing its sensitivity and discriminatory power substantially. This is corroborated by results from a study among patients to receive hip replacement surgery in the UK. Not a single patient reported a level 3 problem on mobility on the 3L, whereas there were many reported problems with mobility in the Oxford Hip Score, a condition-specific measure [59]. Changing the most severe level descriptor of 3L ‘confined to bed’ to ‘unable to walk about’ in 5L appeared to be a huge improvement.

A final implication of our study includes the introduction of a powerful evaluative framework, allowing for further extension by using evidence resulting from longitudinal 3L–5L data. Our framework combines parametric (F statistic) with non-parametric (AUROC) methods, and may be more broadly applied than assessing granularity of the system (the number of response options), such as to investigate the impact of adding dimensions to the EQ-5D, or assessing translation effects.

The current 5L system would profit from more knowledge on the random error of descriptive data (reliability) and cut-point effects, which would also be useful in the development of any new measure. This includes investigating whether the latent scale people use when responding to the EQ-5D for self-classification is the same as when valuing hypothetical health states.

Appendix

See Table 6 and Fig. 9.

Table 6 Mean EQ-5D-3L and EQ-5D-5L utility values and standard deviations by condition group for seven countries and the transformed Level Sum Score

Fig. 9

Histograms of all possible 3L (n = 243) and 5L (n = 3125) utility values based on value sets from seven countries. 3L EQ-5D-3L, 5L EQ-5D-5L