Abstract
Background
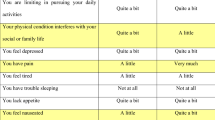
The EORTC QLU-C10D is a new multi-attribute utility instrument derived from the widely used cancer-specific quality-of-life (QOL) questionnaire, EORTC QLQ-C30. The QLU-C10D contains ten dimensions (Physical, Role, Social and Emotional Functioning; Pain, Fatigue, Sleep, Appetite, Nausea, Bowel Problems), each with four levels. To be used in cost-utility analysis, country-specific valuation sets are required.
Objective
The aim of this study was to provide Australian utility weights for the QLU-C10D.
Methods
An Australian online panel was quota-sampled to ensure population representativeness by sex and age (≥ 18 years). Participants completed a discrete choice experiment (DCE) consisting of 16 choice-pairs. Each pair comprised two QLU-C10D health states plus life expectancy. Data were analysed using conditional logistic regression, parameterised to fit the quality-adjusted life-year framework. Utility weights were calculated as the ratio of each QOL dimension-level coefficient to the coefficient on life expectancy.
Results
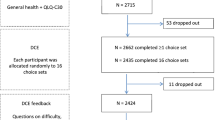
A total of 1979 panel members opted in, 1904 (96%) completed at least one choice-pair, and 1846 (93%) completed all 16 choice-pairs. Dimension weights were generally monotonic: poorer levels within each dimension were generally associated with greater utility decrements. The dimensions that impacted most on choice were, in order, Physical Functioning, Pain, Role Functioning and Emotional Functioning. Oncology-relevant dimensions with moderate impact were Nausea and Bowel Problems. Fatigue, Trouble Sleeping and Appetite had relatively small impact. The value of the worst health state was -0.096, somewhat worse than death.
Conclusions
This study provides the first country-specific value set for the QLU-C10D, which can facilitate cost-utility analyses when applied to data collected with the EORTC QLQ-C30, prospectively and retrospectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
This study provides the first value set (i.e. set of utility weights) for the EORTC QLU-C10D, a new preference-based multi-attribute utility instrument derived from the widely used cancer-specific quality-of-life questionnaire, EORTC QLQ-C30. |
Cost-utility analysis (CUA) represents a major part of the reimbursement process in many countries. The availability of the EORTC QLU-C10D will facilitate CUA for cancer interventions, as it can be applied to data collected with the EORTC QLQ-C30, prospectively and retrospectively. |
Sizeable utility decrements associated with cancer-sensitive dimensions, notably nausea, bowel problems and appetite, may make the QLU-C10D more sensitive than generic measures in CUA. Future research is required to assess this in datasets containing both the QLQ-C30 and a generic utility instrument. |
1 Introduction
Economic evaluation is central to the evaluation of new therapies and technologies in many countries. Cost-utility analysis (CUA) is a form of economic evaluation that quantifies health outcomes on a standardised metric, typically the quality-adjusted life-year (QALY). The quality adjustment is provided by a ‘value set’; that is, a set of utility weights for a range of possible health states within any given health state classification system. Value sets can be derived for classification systems originally developed as multi-attribute utility instruments (MAUI), or by adaptation of existing health-related quality of life (HRQoL) profile measures [1, 2]. Such a measure, the EORTC QLQ-C30, is a widely used core questionnaire in the modular HRQoL suite of the European Organisation for Research and Treatment of Cancer (EORTC) [3].
The Multi-Attribute Utility in Cancer (MAUCa) Consortium aims to facilitate the use of HRQoL data in CUA in cancer settings by providing a series of country-specific value sets for the QLQ-C30. To this end, we have developed a health state classification system containing 13 of the QLQ-C30’s 30 items, combined into ten dimensions (Table 1) [4] and a valuation method based on a discrete choice experiment (DCE) [5]. These are key components of the QLU-C10D, a new cancer-specific MAUI. The aim of this current paper is to apply the valuation method in an Australian general population sample to produce the first country-specific utility weights for the QLU-C10D.
2 Methods
2.1 The QLU-C10D
Table 1 shows the QLU-C10D health state classification system, and explains how the ten dimensions, each with four levels, map to 13 of the 30 items in the QLQ-C30. The derivation of this health state classification system is described elsewhere [4].
2.2 The Valuation Task: Discrete Choice Experiment (DCE) Presentation
The valuation task was based on methods developed for the Australian valuations for the EQ-5D(3L) and SF-6D instruments [6, 7]. The task involved choosing between two QLU-C10D health states, each with a specified duration (life years), described as ‘Situation A’ and ‘Situation B’ (Fig. 1). Because the QLU-C10D includes more dimensions than the EQ-5D(3L) or SF-6D, we first established the feasibility of the task, and pilot tested the DCE task wording, layout and presentation formats [5]. Choice sets were presented in a format preferred by participants in the QLU-C10D valuation methods experiment [5]; that is, dimensions that differed between situations A and B were highlighted in yellow. For the Physical Functioning dimension, the descriptors for levels 2 and 3 are quite complex (Table 1). To facilitate respondent understanding, we presented the two component items, ‘long walk’ and ‘short walk’, as two separate attributes in the survey (Fig. 1). Note that the Physical Functioning dimension was treated as one four-level dimension in the DCE design (online resource 1, see electronic supplementary material [ESM]) and data analysis.
2.3 Health States Valued: DCE Design
The QLU-C10D health state classification system has over a million possible health states (410 = 1,048,576). We employed a designed experiment to select 960 choices sets that would maximise statistical efficiency in estimating the utility model parameters. Health states were operationalised as 12 attributes in the DCE: one for duration, two to represent physical functioning (long and short walk), and one for each of the remaining nine QLU-C10D dimensions. Because 12 dimensions is a relatively large number for respondents to consider simultaneously, we simplified the cognitive task by constraining the number of HRQoL dimensions that differed between health states in any given choice set to four, as done in the QLU-C10D valuation methods experiment [5], using the same experimental design. Briefly, we began with a balanced incomplete block design (BIBD) to define which four of the ten QLU-C10D dimensions differed within choice sets [8]. This BIBD was then duplicated. To determine the levels of these differing dimensions, a generator-based approach was employed, designed to allow estimation of main effects and all two-factor interactions involving duration [9]. The levels of the six dimensions that were constant between options were then developed using an orthogonal main effects plan. This follows the approach outlined by Demirkale et al. [10]. The final design comprised 1920 health states in 960 choice sets (online resource 1, see ESM).
There were two levels of randomisation in the DCE component of the survey: (i) each respondent was randomly allocated 16 of the 960 choice sets without replacement; (ii) which option was seen as Situation A or B was randomised within each choice set to mitigate any ordering bias. The dimensions were always presented in the same order, as previous work showed that dimension order does not systematically bias utility weights for the QLU-C10D [11].
2.4 Survey Content
All survey content was developed by the MAUCa Consortium. In addition to the DCE, the survey contained other components (Fig. 2). The self-reported health questions included the general health question of the SF-36 [12] and the Kessler-10 (mental health) questionnaire [13]. Sociodemographic questions were worded such that they could be mapped directly to normative data to enable assessment of our sample’s representativeness of the Australian general population (Table 2).
2.5 Survey Implementation and Sample Recruitment
The content was implemented as an online survey by SurveyEngine [14], a company that specialises in choice experiments. SurveyEngine and its panel providers comply with the International Code on Market, Opinion and Social Research and Data Analytics [15]. SurveyEngine managed recruitment (via an Australian online panel provided by Toluna), administration of the survey and data collection. The target population was the Australian adult general population (aged ≥ 18 years). Participants were panel members aged 18 years or older who opted in to the survey. There were no exclusion criteria. Quota sampling by age and sex was used to achieve population representativeness on those variables.
2.6 Statistical Analysis
2.6.1 Sample Representativeness
Chi-square tests were used to assess our sample’s representativeness of the Australian population for age and sex (population data available from the Australian Bureau of Statistics as at March 2013 [16]); self-reported general health, Aboriginal and Torres Strait Islander (ATSI) status, highest level of education, and country of birth (population data available from the Household, Income and Labour Dynamics in Australia Surveys [HILDA], Wave 10 [17]); self-reported mental health (Kessler-10 Australian norms from the 2007 Australian National Health Survey [18]).
2.6.2 Utility Estimation
The DCE data were analysed in the statistical software package STATA-13 [19] using a functional form used previously to estimate utilities from DCE data consistent with standard QALY model restrictions [5,6,7, 20, 21]. The QALY model requires that all health states have zero utility at death (i.e. ‘the zero condition’) [22, 23]. A functional form that satisfied this requirement included the QLU-C10D dimension levels interacted with the duration variable (‘TIME’) (Eqs. 1, 2). Thus, as TIME tended to zero, the systematic component of the utility function tended to zero. Another requirement of the QALY model is constant proportional time trade-off, therefore the relationship between utility and TIME (life years) was constrained to be linear.
A useful feature of this functional form was that the impact of moving away from level 1 (no problems) in each dimension was characterised through the two-factor interaction term with duration (note that the experimental design allowed for all these interactions). This enabled a utility algorithm in which the effect of each level of each dimension could be included as a decrement away from full health (which had a value of 1).
We analysed the data in two ways, reflecting different approaches to modelling heterogeneity (Eqs. 1, 2). The primary analysis was underpinned by Eq. 1, in which the utility of option j in choice set s for survey respondent i was assumed to be
where α was the utility associated with a life year, \(X_{isj}^{'}\) was a vector of dummy variables representing the levels of the QLU-C10D health state presented in option j, and β was the corresponding vector of utility weights associated with each level in each dimension within \(X_{isj}^{'}\), for each life year. The error term \(\varepsilon_{isj}\) was assumed to have a Gumbel distribution.
In the primary analysis, DCE responses were estimated as a conditional logit model. To adjust the standard errors to allow for intra-individual correlation (as each respondent was asked to consider 16 DCE choice sets), we used a clustered sandwich estimator implemented by STATA’s vce (cluster) option. To estimate utility decrements for each movement away from level 1 (no problems) in each of the ten QLU-C10D dimensions, we divided each of the β terms by α. To estimate confidence intervals around these ratios, we used STATA’s wtp command [23], using the delta method.
Model 1 included every move away from the best level (level 1, no problems) in each dimension within \(X_{isj}^{'}\). Thus, \(X_{isj}^{'}\) contained 30 terms (i.e. 10 dimensions × [4−1] levels within each). If non-monotonicity was observed among levels within a dimension in Model 1 estimates, the non-monotonic levels were combined in Model 2. This restriction has been standardly imposed in previous studies [24,25,26,27,28,29].
In a secondary approach, we employed a mixed logit [30]. In Model 3, it was assumed that coefficients were drawn from a distribution, allowing for preference heterogeneity among individuals.
Thus, α and the vector of βs now represent population mean preferences, while γ i and η i are individual deviations around those mean preferences. These deviations were assumed to be distributed multivariate normal (0,∑). We used the mixlogit STATA command [31] to estimate α, the vector of βs and the standard deviations of γ and the vector of ηs, with one adjustment. The standard command limits the number of parameters drawn from a distribution at 20. To allow all 31 coefficients (including duration) to be drawn from a distribution, we used pseudo-random draws (personal communication, Arne Risa Hole, Department of Economics, University of Sheffield, 15 June 2015).
To compare models in terms of model fit, Akaike information criterion (AIC) and Bayesian information criterion (BIC) estimates are presented.
3 Results
3.1 Sample Characteristics and Representativeness
Figure 2 shows the recruitment flow, response rates and sample sizes for each component of the survey, and Table 2 shows the sample characteristics relative to population norms. While the sample differed statistically from the general population in all measured characteristics except age and sex, differences were generally small (≤ 3% in any one category). Notable exceptions were education (university education over-represented by 18%) and mental health (Kessler-10 sample mean was in the ‘medium risk’ range of anxiety or depressive disorder while the general population mean was in ‘low or no risk’ range).
3.2 Utility Estimates
Additional years of life were preferred, and all movements away from ‘no problems’ in each dimension were valued negatively (Model 1, Table 3), except level 2 of Social Functioning (value zero). Moving to worse levels in each dimension was associated with an absolutely larger coefficient, with only two exceptions. The worst two levels of the Sleep and Appetite dimensions were not monotonically ordered, but both violations of monotonicity were small (0.003 and 0.007, respectively).
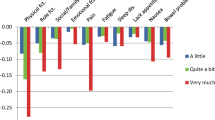
Model 2 constrained the coefficients for levels 3 and 4, respectively, of the Sleep and Appetite dimensions to have the same coefficient, with very little loss of model fit (Table 3). The utility decrements for each level of each dimension from Model 2 are reported in Table 4 with corresponding 95% confidence intervals, and graphed in Fig. 3. The largest utility decrements were associated with physical, role, social and emotion functioning and pain. Sizeable decrements were associated with nausea, bowel problems and appetite, while smaller decrements were associated with problems with sleep and fatigue.
In the mixed logit results (Model 3, online resource 2, see ESM), the mean of the distributions for each of the coefficients were generally monotonic, with four exceptions. Three dimensions had small positive estimates for level 2, but none were statistically different from zero: Social Functioning (p = 0.56), Emotional Functioning (p = 0.93) and Fatigue (p = 0.81). For Appetite, levels 3 and 4 were non-monotonic (as in Model 1).
Figure 4 compares the utility decrements from Models 1 and 3, showing a strong relationship between corresponding estimates from the conditional logit and mixed logit models. The coefficients from Model 1 were absolutely larger than those from Model 3, meaning the spread of the resultant utility algorithm was slightly larger.
3.3 QLU-C10D Utility Calculation
The utility decrements from Model 2 (Table 4) provide the weights, w dl , for calculating QLU-C10D scores from QLQ-C30 responses (Eq. 3). Note that first, QLQ-C30 items must be converted to QLU-C10D levels, as shown in Table 1. A utility score of 1 is assigned to patients whose QLQ-C30 scores indicate they are at level 1 of all ten dimensions of the QLU-C10D. For all other health states, the utility score is 1 minus each utility decrement (w dl ) for each level down from no problems in each of the ten QLU-C10D dimensions. Thus, the QLU-C10D utility score for patient p, determined by their QLU-C10D level l for each dimension d, is
For example, a health state with quite a lot of problems with Role Functioning, a little problem with Emotional Functioning, and a little Nausea, but no problems in any other dimensions, would be valued at 1 − the decrements for Role Functioning level 3, Emotional Functioning level 2 and Nausea level 2 = 1 − (0.09 + 0.02 + 0.047) = 0.843. By convention, the health states would be described as 1312111121. The best possible health state (1111111111) has a value of 1, and the worst possible state (4444444444) has a value of −0.096.
Appendix 3 in online resource 3 (see ESM) provides detailed instructions on calculating utility weights for all the QLU-C10D health states, and provides STATA and SPSS syntax code to implement this.
When asked about the difficulty of this survey compared with other surveys they had done, 28% of respondents reported the DCE questions to be ‘about the same’ level of difficulty and 39% felt it was ‘harder’. Most (76%) felt the presentation of the health states was clear or very clear. While 39% felt it was difficult or very difficult to choose between pairs of health states, 33% felt it was easy or very easy. Detailed participant feedback on the DCE task will be published separately.
4 Discussion
This paper reports the first value set for the QLU-C10D, a MAUI derived from the EORTC QLQ-C30. This approach has two important advantages. First, it allows direct quantification of utility for use in economic evaluation from responses to the QLQ-C30, a widely used cancer-specific HRQoL questionnaire. Second, it captures dimensions related to cancer symptoms that are not included in generic instruments (particularly appetite, nausea and bowel problems). The main drivers of utility were the generic dimensions, with the largest utility decrements for physical, role, social and emotion functioning and pain, mirroring generic MAUIs. However, sizeable decrements were associated with cancer-sensitive dimensions, particularly nausea, bowel problems and appetite. Problems with sleep and fatigue were smaller, perhaps because minor problems with sleep and fatigue are relatively common and therefore considered less important by survey respondents. It is possible that the size of relative utility weights would differ for cancer patients with experience of extreme levels of fatigue and sleep disturbance. The MAUCa Consortium is exploring this question in a related study currently underway, sampling Austrian patients and general population. Even though the utility decrements for the cancer-sensitive dimensions were smaller than those for the more generic dimensions, their inclusion provides a more relevant measure of utility for cancer interventions.
Physical functioning had larger utility decrements than other dimensions, for each level. In the QLU-C10D, physical functioning is represented by walking, making it somewhat comparable to the EQ-5D Mobility and HUI3 Ambulation dimensions. In the HUI3 multi-attribute utility function, Ambulation does not have the largest utility decrements for any level [32]. Results from EQ-5D valuation studies are mixed. For example, in Australian valuations of the EQ-5D(3L) using DCE, Mobility had the largest utility decrement of all dimensions at level 3 but not level 2 [33], while in Australian EQ-5D(3L) valuations using time trade-off (TTO), Anxiety/Depression and Pain/Discomfort had the largest utility decrements at level 3, and at level 2 Mobility had the second lowest utility decrement [34]. Why might ability to walk have the largest impact on utility in the current study? First, physical functioning appeared as the first dimension in the choice set, as in the QLQ-C30 parent questionnaire. However, we have previously investigated and dismissed order effect after randomised testing in DCEs for both QLU-C10D [11] and EQ-5D-5L [35]. Second, due to the complexity of the level descriptors, physical functioning appeared in the DCE as two attributes, even though it was a single four-level dimension in the DCE experimental design and analysis. A useful comparator here is the EORTC-8D, where Physical Functioning was presented as a single five-level dimension (representing the same QLQ-C30 long/short walk items as in the QLU-C10D) [27]. It had the third largest utility decrement for the worst level (exceeded by Social and Emotional Functioning) and the second largest for level 2 (exceed by Pain). While country is a confounder of this comparison, this issue cannot be ruled out as a driver of the effect, but will be resolved soon as UK valuations of the QLU-C10D are underway. Finally, the QLU-C10D Physical Functioning dimension covers a large range of mobility with four levels reflecting the combined range of the two QLQ-C30 walking items (see Table 1), while other dimensions are based on the range in only one item. It may therefore be appropriate that the utility decrements are correspondingly large.
In similar studies, initial models have contained some inconsistent orderings of utility decrements within dimensions, particularly for dimensions with small utility impacts [24,25,26,27,28,29]. Consistent with previous studies, we imposed constraints to remove non-monotonicities. This did not reduce model fit markedly, and avoids perverse results in QALY calculations.
Anchors at one (full health) and zero (death) are imposed by the QALY model, but there is no natural anchor for the pits state (worst possible health state). The QLU-C10D pits state value is -0.095. This is considerably lower than the 0.29 pits state value for the QLU-C10D’s precursor, EORTC-8D [27], which has eight of the ten QLU-C10D dimensions (four with exactly the same items and levels as the QLU-C10D, four that differ slightly), but lacks Sleep and Appetite. In our study, the worst levels of Sleep and Appetite had a combined utility decrement of 0.09, so the difference in content explains some of the difference in pits state values. Since the EORTC-8D was valued with TTO in the United Kingdom (UK) general population, valuation method and country likely explain much of the remainder, as both instruments share a simple additive utility function. The values of the pits state in the original UK and Australian EQ-5D(3L) TTO studies were −0.594 [36] and −0.217 [34], respectively, and in the Australian EQ-5D(3L) DCE study it was −0.516 [33]. Variations in the value of health states, including the pits state, are driven by several factors [37], including country-specific cultural differences in attitudes to trading between mortality and morbidity, different health state classification system content, valuation method and utility functional form. Arguably, a lower pits state value means a greater range in a value set which may lead to greater differences between interventions in CUA. A related issue is sensitivity to mild impairments. Values for health states with level 2 across all dimensions were 0.464 for the QLU-C10D (Australian DCE) and 0.715 for the EORTC-8D (UK TTO). Assessing the sensitivity of the QLU-C10D to differences in mild and extreme QOL impacts, and comparing this with other candidate MAUIs, are important issues for future research.
The DCE method has emerged as an alternative to TTO and standard gamble (SG) methods for valuation of health outcomes in the past decade, and has now been used in a number of studies [6, 20, 21, 33, 38, 39]. The discrete choice method is attractive for several reasons: it is embedded in a strong theoretical measurement framework; it utilises well established statistically robust experimental design and modelling methods; it is based on a relatively simple judgmental task; it is feasible with online recruitment and data collection. The use of DCEs to value health states is maturing, but still presents some challenges. While the judgmental task is simple relative to TTO and SG, thus allowing survey respondents to consider a larger number of attributes, the 12 attributes in the current study is a relatively large number. This study confirms the QLU-C10D valuation methods experiment in finding this is feasible for respondents [5]. We reduced cognitive challenge firstly by allowing only four dimensions to differ in each choice set and secondly by presenting choice sets in the format preferred by participants in the methods experiment, using yellow highlighting to identify differences between situations A and B [5]. Allowing only some dimensions to differ across choice sets has the additional advantage of requiring respondents who employ heuristics such as considering a single attribute to trade off between other attributes. We designed an experiment with 960 choice sets that would maximise statistical efficiency in estimating utility parameters. This meant the survey included some health states that might seem rather unlikely to respondents, such as severe vomiting yet no problems with social function. However, we note that in the patient-reported QLQ-C30 data used to derive the QLU-C10D health state classification system, at least one patient reported each pairwise combination of levels [4].
We used two modelling approaches, conditional logit and mixed logit, which yielded similar mean utility decrements. We have chosen conditional logit (Model 2) as the basis for calculating utilities for CUA for the following reasons: (i) for economic evaluation, we are generally most interested in the mean response, so preference heterogeneity is a secondary concern; (ii) to our knowledge, there remains uncertainty about the appropriate distributional assumptions for the mixed logit.
This study has several strengths and some limitations. It provides a preference-based measure for calculating utilities for the QLQ-C30, which is theoretically and empirically stronger than using mappings of the EORTC QLQ-C30 to other preference-based utility measures [40]. The development of the health state classification system was psychometrically thorough [4]. The valuation survey sample was large, with quota sampling achieving population representativeness for age and sex. The extent to which non-representativeness on the other measured sociodemographic variables is a limitation is as yet unknown, and will be explored in future researching by pooling valuation data across the MAUCa Consortium. We established the feasibility of our DCE method [5], and have noted its strengths and limitations above. We used modelling approaches appropriate to our data structure and analysis purpose. Our choice of a monotonic main-effects model for calculating utility is readily accessible for a range of end users, clinically interpretable and consistent with the EORTC quality-of-life conceptual model.
The appropriateness of disease-specific utility weights for CUA is debated by health economists [41]. Conventionally, generic MAUIs such as the EQ-5D are used, primarily to enable comparability across health conditions and interventions. However, the capacity of generic instruments to capture clinically relevant differences in cancer is also debated [42,43,44]. Arguably, the QLU-C10D should provide a more cancer-sensitive measure of utility than provided by generic MAUIs, although this is yet to be tested empirically. Further, data on generic utility measures may not always be available. The QLU-C10D enables utility values to be retrospectively generated from the wealth of existing QLQ-C30 data, thus facilitating economic evaluation from existing studies. It is anticipated that the QLU-C10D will have good psychometric properties, and future research will examine this, as well as assessing its performance relative to generic MAUIs.
The QLU-C10D has been developed by the MAUCa Consortium in collaboration with the EORTC QOL Group. A key strength of the Consortium’s approach is the use of identical valuation methods across countries, creating a unique opportunity to explore predictors of health outcome values, including country, age, sex, education and health status of valuation survey respondents—this will be done in future analyses.
The QLU-C10D is endorsed by the EORTC QOL Group, and supersedes the EORTC-8D. Notably, the development of the health state classification system of the EORTC-8D was based on data from 655 multiple myeloma patients, while that of the QLU-C10D was informed by a much larger (n = 2616) and more diverse sample: 13 countries, 15 primary cancer types, localised/regional (n = 1037) and recurrent/metastatic stages (n = 1579) [4]. The EORTC QOL Group now has stewardship of the QLU-C10D, being responsible for all aspects of its management, developing and maintaining information regarding administration, scoring and interpretation, and housing relevant materials on the EORTC QOL website. This will make the QLU-C10D widely available for use prospectively and retrospectively, and thereby facilitate the incorporation of quality of life into healthcare decision-making for cancer care.
5 Conclusions
CUA represents a major part of the reimbursement process in many countries. In Australia, the government guidelines for preparing submissions to the Pharmaceutical Benefits Advisory Committee (PBAC) favour direct estimation of utilities over mapping, do not mandate a particular MAUI but prefer Australian-based preference weights and encourage the use of patient-reported outcomes/MAUIs that capture all important disease- or condition-specific factors [45; pages 37, 77]. Based on the experience of RV and RN serving on PBAC and its subcommittees, submissions for cancer interventions frequently present QLQ-C30 data. Therefore, the value set presented here will aid Australian resource allocation decisions. Further, the methods presented in this paper provide a template for further international valuations of the QLU-C10D. A number of these are underway, using exactly the same DCE design, presentation format and analysis, including Austria, Canada, France, Germany, Poland, the UK and the US, enabling assessment of international comparability of preferences for cancer-specific health states.
Data Availability Statement
The dataset generated during the current study will not be publicly available until all planned analyses are complete (see Sect. 4). For updates, please contact the EORTC Quality of Life Group Health Technology Committee.
References
Brazier JE, Rowen D, Mavranezouli I, Tsuchiya A, Young T, Yang Y, et al. Developing and testing methods for deriving preference-based measures of health from condition specific measures (and other patient based measures of outcome). Health Technol Assess. 2012;16(32):1–114.
Rowen D, Brazier J, Ara R, Azzabi Zouraq I. The role of condition-specific preference-based measures in health technology assessment. Pharmacoeconomics. 2017. doi:10.1007/s40273-017-0546-9.
Aaronson NK, Ahmedzai S, Bergman B, Bullinger M, Cull A, Duez NJ, et al. The European Organisation for Research and Treatment of Cancer QLQ-C30: a quality-of-life instrument for use in international clinical trials in oncology. J Natl Cancer Inst. 1993;85(5):365–76.
King MT, Costa DS, Aaronson NK, Brazier JE, Cella DF, Fayers PM, et al. QLU-C10D: a health state classification system for a multi-attribute utility measure based on the EORTC QLQ-C30. Qual Life Res. 2016;25(3):625–36. doi:10.1007/s11136-015-1217-y.
Norman R, Viney R, Aaronson NK, Brazier JE, Cella DF, Costa DS, et al. Using a discrete choice experiment to value the QLU-C10D: feasibility and sensitivity to presentation format. Qual Life Res. 2016;25(3):637–49. doi:10.1007/s11136-015-1115-3.
Norman R, Viney R, Brazier JE, Burgess L, Cronin P, King MT, et al. Valuing SF-6D health states using a discrete choice experiment. Med Decis Mak. 2014;34(6):773–86.
Viney R, Norman R, King MT, Cronin P, Street DJ, Knox S, et al. Time trade-off derived EQ-5D weights for Australia. Value Health. 2014;14(6):928–36.
Colbourn CJ, Dinitz JH. Handbook of combinatorial designs. discrete mathematics and its applications. Boca Raton: Taylor and Francis Group; 2006.
Street DJ, Burgess L. The construction of optimal stated choice experiments: theory and methods. Wiley Series in Probability and Statistics. Hoboken: Wiley; 2007.
Demirkale F, Donovan D, Street DJ. Constructing D-optimal symmetric stated preference discrete choice experiments. J Stat Plan Inference. 2013;143:1380–91.
Norman R, Kemmler G, Viney R, Pickard AS, Gamper EM, Holzner B, et al. Order of presentation of dimensions does not systematically bias utility weights from a discrete choice experiment. Value Health. 2016;19(8):1033–8. doi:10.1016/j.jval.2016.07.003.
Ware JE Jr, Gandek B. Overview of the SF-36 Health Survey and the International Quality of Life Assessment (IQOLA) Project. J Clin Epidemiol. 1998;51(11):903–12.
Kessler RC, Andrews G, Colpe LJ, Hiripi E, Mroczek DK, Normand SL, et al. Short screening scales to monitor population prevalences and trends in non-specific psychological distress. Psychol Med. 2002;32(6):959–76.
P/L S. SurveyEngine Choice Modelling Process & Method. SurveyEngine Pty Ltd, Carlton North, Vic. 2015. http://surveyengine.com/. Accessed 28 Apr 2017.
ICC/ESOMAR. ICC/ESOMAR International Code on Market, Opinion and Social Research and Data Analytics. 2016. https://www.esomar.org/uploads/public/knowledge-and-standards/codes-and-guidelines/ICCESOMAR-International-Code_English.pdf. Accessed 5 Apr 2017.
Australian_Bureau_of_Statistics. Australian Demographic Statistics—March 2013 Cat. No. 3101.0. Canberra: Australian Bureau of Statistics; 2013.
HILDA_Survey_Team. Families, incomes and jobs, volume 9: a statistical report on waves 1 to 11 of the Household, Income and Labour Dynamics in Australia (HILDA) Survey: Melbourne Institute of Applied Economic and Social Research, The University of Melbourne, Australia; 2014.
Slade T, Grove R, Burgess P. Kessler Psychological Distress Scale: normative data from the 2007 Australian National Survey of Mental Health and Wellbeing. Aust N Z J Psychiatry. 2011;45(4):308–16. doi:10.3109/00048674.2010.543653.
StataCorp. Stata Statistical Software: Release 13. College Station: StataCorp LP; 2013.
Bansback N, Brazier JE, Tsuchiya A, Anis A. Using a discrete choice experiment to estimate societal health state utility values. J Health Econ. 2012;31:306–18. doi:10.1016/j.jhealeco.2011.11.004.
Norman R, Cronin P, Viney R. A pilot discrete choice experiment to explore preferences for EQ-5D-5L health states. Appl Health Econ Health Policy. 2013;11(3):287–98.
Bleichrodt H, Johannesson M. The validity of QALYs: an experimental test of constant proportional tradeoff and utility independence. Med Decis Mak. 1997;17(1):21–32.
Bleichrodt H, Wakker P, Johannesson M. Characterizing QALYs by risk neutrality. J Risk Uncertain. 1997;15(2):107–14. doi:10.1023/a:1007726117003.
Brazier JE, Roberts J, Deverill M. The estimation of a preference-based measure of health from the SF-36. J Health Econ. 2002;21:271–92.
Mukuria C, Rowen D, Brazier JE, Young TA, Nafees B. Deriving a preference-based measure for myelofibrosis from the EORTC QLQ-C30 and the MF-SAF. Value Health. 2015;18(6):846–55. doi:10.1016/j.jval.2015.07.004.
Mulhern B, Rowen D, Jacoby A, Marson T, Snape D, Hughes D, et al. The development of a QALY measure for epilepsy: NEWQOL-6D. Epilepsy Behav. 2012;24(1):36–43. doi:10.1016/j.yebeh.2012.02.025.
Rowen D, Brazier JE, Young T, Gaugris S, Craig BM, King MT, et al. Deriving a preference-based measure for cancer using the EORTC-QLQC30. Value Health. 2011;14(5):721–31.
Rowen D, Mulhern B, Banerjee S, van Hout B, Young TA, Knapp M, et al. Estimating preference-based single index measures for dementia using DEMQOL and DEMQOL-Proxy. Value Health. 2012;15(2):346–56. doi:10.1016/j.jval.2011.10.016.
Stevens K. Valuation of the Child Health Utility 9D Index. Pharmacoeconomics. 2012;30(8):729–47. doi:10.2165/11599120-000000000-00000.
Revelt D, Train K. Customer-specific taste parameters and mixed logit. Berkeley: University of California; 1999.
Hole A. Fitting mixed logit models by using maximum simulated likelihood. STATA J. 2007;7:388–401.
Feeny D, Furlong W, Torrance GW, Goldsmith CH, Zhu Z, DePauw S, et al. Multiattribute and single-attribute utility functions for the health utilities index mark 3 system. Med Care. 2002;40(2):113–28.
Viney R, Norman R, Brazier JE, Cronin P, King MT, Ratcliffe J, et al. An Australian discrete choice experiment to value EQ-5D health states. Health Econ. 2014;23(6):729–42. doi:10.1002/hec.2953.
Viney R, Norman R, King MT, Cronin P, Street DJ, Knox S, et al. Time trade-off derived EQ-5D weights for Australia. Value Health. 2011;14(6):928–36. doi:10.1016/j.jval.2011.04.009.
Mulhern B, Norman R, Lorgelly P, Lancsar E, Ratcliffe J, Brazier J, et al. Is dimension order important when valuing health states using discrete choice experiments including duration? Pharmacoeconomics. 2017;35(4):439–51. doi:10.1007/s40273-016-0475-z.
Dolan P. Modelling valuation for Euroqol health states. Med Care. 1997;35:351–63.
Norman R, Cronin P, Viney R, King MT, Street D, Ratcliffe J. International comparisons in valuing EQ-5D health states: a review and analysis. Value Health. 2009;12(8):1194–200.
Bansback N, Hole AR, Mulhern B, Tsuchiya A. Testing a discrete choice experiment including duration to value health states for large descriptive systems: addressing design and sampling issues. Soc Sci Med. 2014;114:38–48. doi:10.1016/j.socscimed.2014.05.026.
Stolk E, Oppe M, Scalone L, Krabbe PFM. Discrete choice modeling for the quantification of health states: the case of the EQ-5D. Value Health. 2010;13(8):1005–13.
McTaggart-Cowan H, Teckle P, Peacock S. Mapping utilities from cancer-specific health-related quality of life instruments: a review of the literature. Expert Rev Pharmacoecon Outcomes Res. 2013;13(6):753–65.
Versteegh MM, Leunis A, Uyl-de Groot CA, Stolk EA. Condition-specific preference-based measures: benefit or burden? Value Health. 2012;15(3):504–13. doi:10.1016/j.jval.2011.12.003.
Brazier JE, Rowen D, Mavranezouli I, Tsuchiya A, Young T, Yang Y, et al. Developing and testing methods for deriving preference-based measures of health from condition-specific measures (and other patient-based measures of outcome). Health Technol Assess (Winchester, England). 2012;16(32):1–114. doi:10.3310/hta16320.
Goodwin E, Green C. A systematic review of the literature on the development of condition-specific preference-based measures of health. Appl Health Econ Health Policy. 2016;14(2):161–83. doi:10.1007/s40258-015-0219-9.
Wailoo A, Davis S, Tosh J. The incorporation of health benefits in cost utility analysis using the EQ-5D. Decision Support Unit, School of Health and Related Research, University of Sheffield. 2010.
Pharmaceutical Benefits Advisory Committee. Guidelines for preparing submissions to the Pharmaceutical Benefits Advisory Committee (PBAC). Version 5.0, September 2016. Department of Health Canberra. 2016. https://pbac.pbs.gov.au/. Accessed 5 Sept 2017.
Acknowledgements
MAUCa Consortium members: N. Aaronson, J. Brazier, D. Cella, D. Costa, P. Fayers, P. Grimison, M. Janda, G. Kemmler, M. King (Chair), H. McTaggart-Cowan, R. Mercieca-Bebber, R. Norman, S. Peacock, S. Pickard, D. Rowen, G. Velikova, R. Viney, D. Street, T. Young.
Author information
Authors and Affiliations
Consortia
Contributions
M. King is the guarantor of this manuscript—she takes responsibility for the quality of the research methods and the accuracy of the manuscript’s content. All authors were involved in the conception and planning of the work that led to the manuscript and interpretation of the data. MK, RN, DC and RM-B were also involved in acquisition and analysis of the data. MK, RN and RV wrote the first draft of the manuscript. All authors critically revised the manuscript and approved the final version for publication.
Corresponding author
Ethics declarations
Funding
This research was funded by the National Health and Medical Research Council of Australia (Project Grant 632662). Dr Norman was supported by a NHMRC Early Career Research Fellowship (1069732). Professor King was supported by the Australian Government through Cancer Australia.
Conflict of interest
Authors King, Viney, Pickard, Rowen, Aaronson, Brazier, Cella, Costa, Fayers, Kemmler, McTaggart-Cowen, Mercieca-Bebber, Peacock, Street, Young and Norman each declare that they have no conflicts of interest in relation to the material reported in this manuscript. For transparency, we declare that authors Viney, Pickard, Brazier and Norman are members of the EuroQoL Group, and authors Aaronson, Fayers, Kemmler and King are members of the EORTC QOL Group.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. The study was approved by the University of Sydney Human Research Ethics Committee, Approval number 2012/2444.
Additional information
Members of the MAUCa Consortium are listed in “Acknowledgements”.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
King, M.T., Viney, R., Simon Pickard, A. et al. Australian Utility Weights for the EORTC QLU-C10D, a Multi-Attribute Utility Instrument Derived from the Cancer-Specific Quality of Life Questionnaire, EORTC QLQ-C30. PharmacoEconomics 36, 225–238 (2018). https://doi.org/10.1007/s40273-017-0582-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40273-017-0582-5