Abstract
Missing data are a frequent problem in cost-effectiveness analysis (CEA) within a randomised controlled trial. Inappropriate methods to handle missing data can lead to misleading results and ultimately can affect the decision of whether an intervention is good value for money. This article provides practical guidance on how to handle missing data in within-trial CEAs following a principled approach: (i) the analysis should be based on a plausible assumption for the missing data mechanism, i.e. whether the probability that data are missing is independent of or dependent on the observed and/or unobserved values; (ii) the method chosen for the base-case should fit with the assumed mechanism; and (iii) sensitivity analysis should be conducted to explore to what extent the results change with the assumption made. This approach is implemented in three stages, which are described in detail: (1) descriptive analysis to inform the assumption on the missing data mechanism; (2) how to choose between alternative methods given their underlying assumptions; and (3) methods for sensitivity analysis. The case study illustrates how to apply this approach in practice, including software code. The article concludes with recommendations for practice and suggestions for future research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Missing data are a frequent problem in cost-effectiveness analysis within a randomised clinical trial. |
Different methods of handling missing data can yield different results and affect decisions on the value for money of healthcare interventions. |
The choice of method should be grounded in the assumed missing data mechanism, which in turn should be informed by the available evidence. |
The impact of alternative assumptions about the missing data mechanism should be carefully assessed in sensitivity analysis. |
1 Introduction
Decisions on whether new interventions are cost effective and should be offered by healthcare services are often informed by a cost-effectiveness analysis (CEA) undertaken within a randomised controlled trial (RCT), referred to as a within-trial CEA. Missing data occur frequently in RCTs: patients may be lost to follow-up, questionnaires may be lost or unreturned and responses to individual questionnaire items may be illegible, nonsensical or non-existent [1]. This is a concern in within-trial CEAs because costs or health outcomes in individuals with missing data may be systematically different from those with fully observed information. Therefore, handling missing data inappropriately can bias the results, make inefficient use of the data available and ultimately mislead resource allocation decisions. This article focuses on within-trial CEAs; however, the principles and methods are also applicable for analysts who wish to estimate resource use, cost or health-related quality of life (HR-QOL) statistics from RCTs for use as inputs to decision models.
A few studies have explored how to handle missing data in within-trial CEAs [2] or for CEA data (costs [3, 4] or quality-of-life data [5, 6]). The general conclusion is that removing individuals with missing data from the analysis or replacing a missing observation with a single predicted value (single imputation) is rarely adequate. Nevertheless, a recent review concluded that most applied within-trial CEAs take the former approach and remove individuals with missing data from the analysis or are unclear on the methodology used [7]. As a result, it can be difficult to understand their assumptions and to use those findings in subsequent research or in resource allocation decisions. These failings may be because the implications of ignoring missing data are not well-known or due to difficulties in implementing more appropriate methods [e.g. multiple imputation (MI), inverse probability weighting (IPW), likelihood-based models] given the following specific characteristics of CEA data. Firstly, costs and quality-adjusted life-years (QALYs), the typical outcomes in CEAs, are cumulative measures derived from longitudinal data collected over the trial follow-up. Each component may have a different missing data pattern. Missing data at one timepoint or for a specific component implies that the aggregate variable is also missing. Given their cumulative nature, these variables can be dealt with at various levels of aggregation (e.g. individual resource use items vs. costs; and dimensions of HR-QOL vs. QALYs). Secondly, both outcomes (costs and QALYs) are non-normally distributed (e.g. QALYs are typically bimodal, left skewed and with a spike at 1), which has implications for the choice of missing data method. Thirdly, they tend to be correlated and the probability of observing one outcome may be dependent on the value of the other. For these reasons, handling missing data in within-trial CEAs can be challenging.
The purpose of this article is to bridge the gap between the methodological literature and applied research by providing a structured approach and practical guidance, including software code, on how to handle missing data in within-trial CEAs. These recommendations are complementary to existing best practice in the conduct and reporting of applied health economic evaluations [8–10] and will be useful for analysts conducting within-trial CEAs as well as for those wishing to estimate costs and QALYs from trial data for use as inputs in modelling. The structured approach follows three principles based on methodological recommendations for the intention-to-treat analysis of RCTs with missing data [11]: (i) the analysis should be based on a plausible assumption for the missing data mechanism; (ii) the method to handle missing data should fit with the assumed missing data mechanism; and (iii) sensitivity analysis should be conducted to explore to what extent the results change with different assumptions. The missing data mechanism refers to whether the probability that data are missing is dependent or independent of observed and unobserved values. Section 2 describes the classification of missing data mechanisms and implications for the choice of method. Sections 3, 4 and 5 describe three stages in the analysis. Section 3 shows how to conduct descriptive analyses to inform a plausible assumption about the missing data mechanism. Section 4 critically reviews alternative methods for handling missing data and their underlying assumptions, in order to help readers choose a suitable method for the base case. Section 5 proposes methods for sensitivity analysis to departures from the chosen assumption on the missing data mechanism. The three-stage approach is illustrated in Sect. 6 with a case study using individual patient data from a published RCT. Section 7 discusses implications and makes recommendations for practice and research. Stata® code is provided in the Electronic Supplementary Material.
2 Classifications of Missing Data Mechanisms
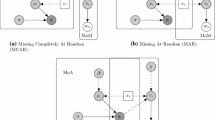
The method to handle missing data should be grounded in a plausible assumption regarding the missing data mechanism. The true mechanism is usually unknown given the observed data. Nonetheless, Rubin’s framework for classifying missing data can help analysts define their assumptions and choose an appropriate analysis method for the base case [12]:
-
Data are missing completely at random (MCAR) if the probability that data are missing is independent of both observed and unobserved values; i.e. the distribution of outcomes in the observed individuals is a representative sample of the distribution of outcomes in the overall population (missing and observed).
-
An extension of Rubin’s MCAR is the covariate-dependent missingness (CD-MCAR); in CD-MCAR, the probability that data are missing may depend on observed baseline covariates (e.g. age and gender) but is independent of the missing and observed outcome [13]. This distinction is useful in within-trial CEAs because RCTs often have multiple data collection points and the probability that data are missing may depend on individuals’ baseline characteristics but not on previous outcome measurements.
-
Data are missing at random (MAR) if the probability that data are missing is independent of unobserved values, given the observed data (including previous outcome measurements). Therefore, any systematic differences between the observed and unobserved values can be explained by differences in observed variables.
-
Data are missing not at random (MNAR) if, given the observed data, the probability that data are missing is dependent on unobserved values. For example, individuals with worse outcomes may be more likely to have missing data on outcomes. Assuming that data are MCAR or MAR when in fact data are MNAR may bias the estimates of treatment effect.
3 Stage 1: Descriptive Analysis of Missing Data
A within-trial CEA should report average HR-QOL scores and average resource use per patient (and average costs prior to handling missing data if applicable) by trial group over time. In addition to these, a descriptive analysis of the missing data helps inform the base-case assumption regarding the missing data mechanism and the range of methods that can be used to handle it. Based on the authors’ experience in conducting analyses with missing data, the descriptive analysis should include the following:
-
(1)
Amount of missing data by trial group at each follow-up period. Data are unlikely to be MCAR if the proportion of missing data differs by treatment allocation (and potentially across different timepoints). Further, any imbalance in the amount of missing data by treatment group increases the sensitivity of the estimated treatment effects to departures from MAR.
-
(2)
Missing data patterns. Graphical tools (such as ‘ misspattern ’ in Stata®) are useful to visualise and understand the pattern of missing data. These graphs indicate whether patients with missing data are lost to follow-up throughout the duration of the trial (monotonic pattern), and therefore whether relatively simpler approaches can be used, such as IPW. In addition, these graphs can be plotted to determine whether data are missing for all the questions in HR-QOL or resource use or for individual items in each category (more detail in Sect. 6.1). These patterns can guide the choice of whether missing data need to be modelled in the individual components or in the aggregate score.
-
(3)
Association between missingness and baseline variables. Logistic regressions can be used to investigate which factors, such as baseline covariates and post-randomisation variables, are associated with the probability of missingness. Data are not MCAR if a baseline variable predicts missingness. Determining whether a specific variable is a predictor of missingness should be based on statistical significance (either univariate or multivariate associations) and on clinical plausibility.
-
(4)
Association between missingness and observed outcomes. Logistic regressions can also explore whether missingness is associated with previously observed outcomes (e.g. costs or HR-QOL score at follow-up). A significant association indicates that data are not CD-MCAR and that MAR may be a more plausible assumption under which to conduct the analysis.
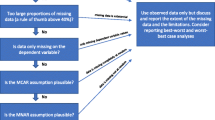
The results of the descriptive analysis should be discussed by the trial team (trialists, clinicians, trial management group, patient involvement group, etc.) to infer possible reasons for missing data and inform the assumption about the missing data mechanism. The descriptive analysis can distinguish between MCAR, CD-MCAR and MAR. However, it is usually impossible to rule out MNAR since the unobserved data are, by definition, unknown. The implications of MNAR should be explored in the sensitivity analysis (see Sect. 5).
4 Stage 2: Choosing and Implementing a Method to Handle Missing Data
The method to handle missing data should fit with the assumption regarding the missing data mechanism and account for the uncertainty around the unknown values. In addition, the method should be able to handle the particular characteristics of CEA data, namely, their longitudinal structure, non-normal distributions and correlations.
4.1 Handling Missing Baseline Values
Missing baseline values can affect the analysis if they are used to predict subsequent missing outcomes or to improve the precision of estimates of treatment effect. Removing individuals with missing baseline data is rarely adequate. Both mean imputation and MI are good options for imputing missing baseline values. Mean imputation fills in each missing value of the baseline covariate with the mean of the observed values and ensures that the imputed values are independent of the treatment allocation [14]. Alternatively, MI can impute the missing baseline covariates when imputing the cost-effectiveness outcomes [15]. MI may be less efficient than mean imputation because it imputes in an arm-dependent way, thereby exacerbating covariate imbalance. Imputing in an arm-dependent way has been shown to be less efficient in imputing missing baselines in RCTs [14].
4.2 Complete Case Analysis, Available Case Analysis and Inverse Probability Weighting
Complete case and available case analyses are valid under MCAR and, if the analysis model includes all baseline variables that predict both outcome and missingness, under CD-MCAR [13]. In complete case analysis (CCA), only individuals with complete data on all variables at all follow-up points are included. This assumes that individuals with complete data are representative of those with missing data, conditional on the variables included in the analysis model. It is inefficient in studies with more than one follow-up assessment because all the information from individuals with at least one assessment missing is discarded. In addition, the analysis cannot be considered ‘intention-to-treat’ because some randomised patients with follow-up data are excluded [11]. CCA is a useful starting point and benchmark but should not constitute the base case for within-trial CEAs.
Available case analysis makes more efficient use of the data than CCA. With available case analysis, the mean costs and QALYs are calculated by treatment group at each follow-up point. Total mean costs and QALYs by treatment group over the whole time horizon are then estimated as the sum of these means. A limitation is that available-case analysis may result in using different samples for the costs and for the health outcomes, which may lead to non-comparability between the patient groups and affect the covariance structure [4].
In IPW, the observed cases are weighted by the inverse of the probability of being observed. IPW is suitable for a monotonic pattern of missing data, in which individuals lost to follow-up do not return to the study. The IPW approach applied to within-trial CEAs has two steps. First, the probability of being observed at each time period is estimated using a Kaplan–Meier survival function, parametric survival curves or logistic regression [1, 16]. IPW assumes MCAR, CD-MCAR or MAR depending on whether the model used to estimate the probability of being observed includes no predictors of missingness, baseline predictors of missingness, or baseline and time-dependent predictors of missingness, respectively. Second, the costs and QALYs of each individual at each time period are weighted by the inverse of the probability of being observed. The mean weighted difference in costs and QALYs and its associated uncertainty can be estimated with regression analysis (e.g. using a system of seemingly unrelated regressions or via bootstrap). IPW can be sensitive to the correct specification of the model estimating the probability of being observed and can give biased estimates if some individuals have very low probabilities of being observed (large weights) [1]. More sophisticated methods have been developed in order to improve precision and reduce the reliance of IPW on the correct specification of the model [17, 18].
In principle, all randomised individuals should be included in the analysis as long as some follow-up data were collected. Individuals with only baseline data typically contribute very little. The impact of including individuals with only baseline data should be explored in a scenario to make the analysis truly intention-to-treat.
4.3 Single Imputation Methods
Imputation methods fill in the missing data with a predicted value. In mean imputation, the missing data are filled in with the unconditional mean of the observed cases. Mean imputation may be valid for missing baseline variables, as noted above, but it is never appropriate for missing outcomes because it underestimates uncertainty. In conditional regression imputation, each missing value is replaced by the predicted value from a regression model conditional on the observed variables, such as baseline covariates and treatment allocation. While this imputation approach assumes MAR, it does not recognise that the imputed values are estimated rather than known. Therefore, this method underestimates the standard errors and distorts the correlation structure of the data, which can affect estimation of the probability that the intervention is cost effective. Last-value carried forward (LVCF) assumes that the outcome remains constant after dropout; i.e. the last observation observed is representative of the missing data in subsequent observations. LVCF has been shown to bias parameter estimates even if data are MCAR [19]. For these reasons, single imputations methods are not appropriate to handle missing data on outcomes.
4.4 Multiple Imputation
MI replaces each missing observation with a set of plausible imputed (predicted) values, drawn from the posterior predictive distribution of the missing data given the observed data. MI can handle both monotonic and non-monotonic missing data under MAR and can be modified to handle MNAR (see Sect. 5). Unlike single imputation methods, MI recognises the uncertainty associated with both the missing data and estimated parameters in the imputation model. It relies on the correct specification of the imputation model, particularly as the amount of missing data increases. Interactions and non-linear terms require specification in advance; therefore, MI may be difficult to implement for a large number of variables (e.g. types of resource use or types of costs).
The MI procedure follows three steps [12]. In step 1, regression models are used to predict plausible values for the missing observations from the observed values. This step has two parts: first, the regression parameters used to predict the values are randomly drawn from their posterior distribution; then, the predicted values are drawn from their posterior predictive distribution. These values are then used to fill in the gaps in the dataset. This process is repeated m times (m being the number of imputations), creating m imputed datasets. Generating multiple datasets reflects the uncertainty arising from imputation. White et al. [20] suggest that, as a rule of thumb, the number of imputed datasets should be similar to the percentage of incomplete cases. In step 2, each dataset is analysed independently using standard methods to estimate the quantity of interest (e.g. expected costs and QALYs in each treatment group over the trial time horizon). Finally, the estimates obtained from each imputed dataset are combined using Rubin’s rules to generate an overall mean estimate of the quantity of interest together with its standard error. Rubin’s rules ensure that the standard error reflects the variability within and across imputations.
There are two main approaches to implementing MI: joint modelling (MI-JM) and chained equations (MICE). MI-JM is a parametric approach where the variables to be imputed are assumed to follow a multivariate normal distribution. This can be an issue for within-trial CEAs since costs and QALYs are usually non-normally distributed, although variables can be transformed to normality [21, 22]. MICE specifies one imputation model for each variable. Imputed values in one variable are used to predict missing values in other variables in an iterative way until the model converges to a stable solution [20]. Theoretically, MICE should accommodate non-normal variables better than MI-JM because the model for each variable can be specified separately (e.g. logistic regression for binary variable, Poisson regression for counts, etc.). However, some simulation studies suggest that MI-JM and MICE can handle non-normality equally well [23, 24]. An advantage of MICE over MI-JM is that MICE can allow for interactions and non-linear terms and incorporate variables that are functions of imputed variables (termed ‘passive variables’), which can be useful in within-trial CEAs (e.g. to predict costs as a function of imputed counts of resource use). In addition, the fully conditional specification of MICE makes it easier to handle datasets with a large number of variables with missing data, which is often the case in within-trial CEAs.
MI can be implemented in Stata® as MI-JM using ‘ mi impute mvn ’ or as MICE using ‘mi impute chained’ or the ‘ ice ’ package. The analysis step can be performed using ‘ mi impute estimate ’ or the ‘ mim ’ package. Multiply imputed data created by ‘ice’ can be imported into ‘ mi impute ’ for analysis using the command ‘ mi import ice ’; otherwise, it can be analysed directly using the ‘mim’ command. Equivalent programmes are available in SAS® and R. The subsequent sections focus on the implementation of MICE because its flexibility makes it more applicable to missing data in within-trial CEAs.
4.4.1 The Imputation Model
Unbiased and reliable imputation of the missing data requires the correct specification of the imputation model, namely which variables to include, how to deal with their distributions and how to capture their correlations. The imputation model should include all variables that are associated with both the missing data and CEA outcomes (costs and health outcomes), and all covariates that are in the analysis model [20]. Although all variables collected in the RCT could, in principle, be included, this can be unwise in practice because a large number of variables can make the model difficult to estimate. Therefore, some selection to identify the most predictive variables may be required. The imputation should be implemented separately by randomised treatment allocation [25]. This explicitly recognises in the imputation model that imputations are different between treatment groups, hence that the posterior distribution of the missing data given the observed may be different between treatment groups. Imputing the treatment groups together but including all possible interactions would only recognise differential means by treatment group and not a differential covariance structure.
Costs and QALYs can be imputed at more or less disaggregated level, from counts of each type of resource use or domains of the HR-QOL instrument to costs or QALYs over the period of follow-up. A balance needs to be struck between maintaining the data structure (hence imputing at more disaggregated level) and achieving a stable imputation model (which becomes more difficult as more variables with missing data are added [26]). The choice of approach should be informed by the structure of the data, the pattern of missing data and by testing a variety of approaches. We tentatively suggest the following:
-
i.
For QALYs, imputing the individual domains may be advantageous if the distribution of HR-QOL scores (typically with a spike at 1 and/or bimodal) is difficult to replicate with an imputation model at the score level or if the individual domains are missing rather than the whole questionnaire. In practice, either approach may be equally valid as suggested by a recent simulation study comparing imputing EQ-5D at individual domains or index score level [27].
-
ii.
For costs, imputing at the total cost level is likely to be appropriate when the different types of resource use that make up the cost have the same pattern of missing data. Since it is generally recommended to report the resource use components [8–10], a pragmatic approach is to impute at both aggregate and disaggregate levels as alternative sensitivity analyses, but having more confidence in the former.
-
iii.
Imputing at the resource use level is probably better when the different types of resource use have different patterns of missing data. If this makes the imputation model difficult to estimate, the key drivers of costs can be imputed at a resource level (e.g. length of stay in hospital, inpatient admissions) and the other items as one cost variable.
Results after imputation should be compared with the descriptive analysis outlined in Sect. 3. Further research on the assessment of these alternative approaches is warranted.
Irrespective of the level of aggregation, data on costs and QALYs are unlikely to be normally distributed. This can be an issue because most readily available software packages that implement MICE tend to rely on normality for the imputation of continuous variables. One option is to transform the data towards normality, e.g. with log transformation. After imputation, the variables are back transformed to the original scale before applying the analysis model. This back transformation does not require correcting for non-normal errors (also referred to as smearing [28]) because the imputed value is drawn from the posterior predictive distribution. Another option is to use predictive mean matching. In predictive mean matching, the missing observation is imputed with an observed value from another individual whose predicted value is close to the predicted value of the individual with the missing observation [29]. This ensures that only plausible values of the missing variable are imputed (e.g. costs are always positive and HR-QOL is always ≤1). Two-part models may be used for variables with a large proportion of zeros (e.g. costs), with or without transforming the non-zero values or in combination with predictive mean matching [30, 31].
Validation is the final step in the development of the imputation model. There is little guidance on how to assess whether the imputation procedure is producing valid results. One option is to assess whether the distributions of observed and imputed values are similar [32, 33]. Another option is to compare the results with an alternative method that assumes the same missing data mechanism.
4.4.2 Analysis of the Multiply Imputed Dataset
A within-trial CEA aims to estimate the average difference in costs and health outcomes between treatment groups, standard errors and correlation as well as the probability that the intervention is cost effective for a particular threshold (or a range of thresholds) and the value of additional information. The average difference in costs and health outcomes and associated uncertainty are straightforward to obtain post-MI with Rubin’s rules. The probability that the treatment is cost effective can also be estimated with Rubin’s rules or using bootstrap. In the former, costs and QALYs are assumed to follow a bivariate normal distribution. The multiply imputed datasets are analysed with a seemingly unrelated regression model [34], combining estimates of mean coefficients and the covariance matrix as per Rubin’s rules. The validity of this approach relies on the multivariate normality of the group-specific mean costs and QALYs; this is often reasonable with moderate sample sizes, even when the individual costs and QALYs are skewed. The alternative approach is to draw bootstrap samples from each of the multiply imputed datasets and estimate the difference in net benefit between the treatment groups in each bootstrap sample (at a given threshold for cost per QALY) [30, 35]. The proportion of bootstrap samples in which the net benefit is positive represents the probability that the treatment is cost effective for each multiply imputed dataset. This probability is then averaged across all multiply imputed datasets. Both approaches are valid because they combine the multiply imputed estimates in a manner that accounts for both the within- and between-imputation variability.
4.5 Likelihood-Based Methods
Likelihood-based methods use all the observed data in a single step to estimate the treatment effect (rather than creating and then analysing the multiply imputed datasets). Likelihood-based models assume MAR conditional on the variables included unless MNAR is explicitly modelled. The effect of the intervention on costs and QALYs can be jointly estimated in order to maintain their correlation structure. Longitudinal data can be handled with a mixed (multilevel) model, where the time-specific effects are modelled as random effects [36].
Likelihood-based methods should lead to similar (and at least as efficient) results when compared to MI when all variables that relate to missingness are included in the analysis model. However, an important limitation is that, in within-trial CEAs, the covariates in the pre-specified analysis model are unlikely to include all variables associated with missingness. In this respect, MI provides more flexibility by allowing the model for the missing data to be estimated separately from the analysis model. In addition, likelihood-based models rely on the correct specification of the model, including its parametric assumptions (e.g. multivariate normality). Since the specification of the model may have an impact on the results, the impact of different specifications should be compared and reported [1].
5 Stage 3: Sensitivity Analysis to the Missing at Random (MAR) Assumption
The sensitivity analysis to the MAR assumption evaluates the impact of assuming that the data are MNAR rather than MAR. In the context of CEA, an important concern is whether the resource allocation decision changes if the data are assumed MNAR; in other words, if individuals with unobserved outcomes have systematically worse or better outcomes than comparable individuals with observed outcomes. Assessment of this specific form of structural uncertainty is relatively well-established in biostatistics but it is rarely undertaken in within-trial CEA. The two main methods for assessing potential departures from MAR are selection models and pattern mixture approaches [1]. As both methods can be difficult for the non-specialist to implement, a practical approximation to the pattern-mixture model is presented in Sect. 6.3. The choice between selection models and pattern mixture approach will depend on which way of expressing differences between the observed and unobserved data is more meaningful for the specific research question being addressed.
Selection models formulate the sensitivity analysis in terms of alternative missing data mechanisms. For example, individuals in worse health may be more likely to have missing data on QALYs. This requires the specification of a model that explicitly recognises the MNAR selection mechanism, which is then fitted jointly with the analysis model for the observed data [37]. Selection models can be approximated using a weighting approach [38]. In this, MI is done under MAR, but the multiply imputed estimates are combined using a weighted version of Rubin’s rules, where imputations more compatible with a proposed MNAR mechanism are given relatively higher weight. The weighting approach tends to fail for large departures from MAR because a small number of imputations is over-weighted.
Pattern mixture modelling formulates sensitivity analysis according to differences between the distribution of the observed and unobserved data. For example, outcomes in individuals with missing data may be worse than those observed in similar individuals with observed data. Under this approach, data are initially imputed under MAR. The distribution of the unobserved values is assumed to shift from the MAR imputation distribution by a sensitivity parameter. The imputed values then are shifted by this sensitivity parameter to give a dataset imputed under MNAR [39, 40]. Results are combined using the usual Rubin’s rules. This is repeated for a range of plausible values for the sensitivity parameter. Either a range of results or the value of the sensitivity parameter required to change the results are reported.
6 Illustration with the REFLUX Study
Data from a published RCT are used to illustrate the structured approach to handle missing data in a within-trial CEA. Descriptive analysis informs the base-case assumption regarding the missing data mechanism. This assumption determines the method used in the base case; other methods are presented for comparison. Sensitivity analysis explores the impact of alternative assumptions on the cost-effectiveness results. Stata® code is provided in the Electronic Supplementary Material.
The REFLUX study was an RCT comparing a policy of offering early laparoscopic fundoplication (with the option of taking medication post-surgery if considered helpful) with a policy of continued medical management, in patients with stable gastro-oesophageal reflux disease eligible for both options over 5 years of follow-up [41]. The aim is to estimate mean differences in costs and QALYs and associated uncertainty and the probability that the intervention (surgery) is cost effective at £20,000 per QALY gained, the conventional threshold used in the UK [9].
6.1 Stage 1: Descriptive Analysis of Missing Data
6.1.1 Amount of Missing Data by Trial Group at Each Follow-Up Period
The REFLUX study collected data on EQ-5D and healthcare resource use by postal questionnaire at 3 and 12 months, and yearly up to year 5. The proportion of individuals with complete data decreased with the duration of follow-up but remained similar between treatment groups (Table 1): from 75 % (year 1) to 65 % (year 5) in the surgery group and from 82 % (year 1) to 63 % (year 5) in the medical management group. In the surgery group, more individuals are observed in year 5 than in year 3; therefore, the missing data do not follow a monotonic pattern; i.e. there are individuals with intermittent missing data (lost to follow-up one year but returned subsequently). IPW would be inappropriate under such patterns. CCA would be, as a minimum, inefficient because it would discard observed data from individuals with some missing outcomes.
6.1.2 Missing Data Patterns
Figure 1 presents the pattern of missing data. As discussed above, missing data is non-monotonic since individuals with missing data at one follow-up may return to the trial subsequently (Fig. 1a and b). For example, some individuals have missing data at 3 months but have complete data in other timepoints. In addition, the pattern of missing data is different for QALYs and costs, but is the same over the different types of resource use (general practitioner visits, hospitalisations and drugs) for each year of follow-up. Therefore, costs can be aggregated at each time period without major loss of information. This pattern reflects the assumption that missing resource use items in questionnaires otherwise filled in meant that no resource was used.
Pattern of missing data. Black shading represents missing data for one or more individuals (arrayed along the horizontal axis) on a particular variable (arrayed along the vertical axis); grey shading represents observed data. a Pattern of missing data on costs. b Pattern of missing data on health-related quality of life (EQ-5D). GP general practitioner
6.1.3 Association Between Missingness and Baseline Variables
Table 2 presents the odds ratios from logistic regressions of indicators of missing cost and QALY data on treatment allocation and a selection of baseline variables. Lower EQ-5D at baseline is associated with missing cost and QALY data. This suggests that the data are unlikely to be MCAR. The other baseline covariates [gender, body mass index (BMI) and age] were associated with missingness but not statistically significant at 5 %. However, all were significant predictors of costs and QALYs at each year (data not shown). This information would support both CD-MCAR and MAR assumptions.
6.1.4 Association Between Missingness and Observed Outcomes
Logistic regressions explored whether missingness is associated with previously observed outcomes by regressing indicators of missing costs or QALYs at each year on their previously observed values (e.g. regressing missing costs in year 2 on costs and QALYs in year 1–3). Most regressions produced statistically insignificant (p > 0.05) results with two exceptions: missing QALYs at year 5 were significantly associated with QALYs at year 3 and 4; missing costs at year 5 were significantly associated with costs at year 3 and QALYs at year 3 and 4. Although these regressions are likely to be affected by multicollinearity, they provide an indication that data are unlikely to be CD-MCAR. Therefore, data are assumed to be MAR. In the analyses that follow, missingness is assumed to depend on baseline covariates (gender, BMI, age, EQ-5D at baseline) and observed costs and QALYs but independent of unobserved costs and QALYs at each year. It is impossible to know whether data are MNAR or MAR from the observed data. Therefore, sensitivity analysis tests the impact of assuming MNAR and the implications of the results for the resource allocation decision.
6.2 Stage 2: Choosing and Implementing a Method to Handle Missing Data
The methods that can handle non-monotonic missing data under the MAR assumption whilst incorporating the uncertainty around the unobserved data and maintaining the correlation structure are MI and likelihood-based methods (specifically, a mixed model to account for the longitudinal nature of the data). The base case uses MI-MICE under MAR. A mixed model is presented as an alternative. CCA, which is not valid under MAR, is presented for comparison.
The MI model uses the baseline covariates, costs and QALYs at each year to impute unobserved costs and QALYs, so that, for example, missing costs at year 5 are imputed using data on baseline covariates, costs at years 1–4 and QALYs at years 1–5. The imputation is run 60 times since there is up to 51 % missing observations. Figure 1 shows that the cost components at any timepoint are either all observed or all missing, so total yearly costs are imputed. Predictive mean matching is used because costs and QALYs are non-normally distributed. The MI model is validated by comparing the distributions of the observed with the imputed data (Fig. 2). The distributions of imputed data are similar to the distribution of the observed data. The multiply imputed datasets are analysed with the same seemingly unrelated regression model used for CCA.
Comparison of the distribution of imputed values (imputation number 1 to 10) with the observed data (imputation number 0) for quality-adjusted life-years and costs in years 1 and 5. Individual values are represented by dots; the width of a row of dots represents the frequency of values in the distribution. QALYs quality-adjusted life-years
The mixed model does not require an imputation step. Costs and QALYs at each year are regressed on time, baseline EQ-5D and treatment allocation. Costs are coded in multiples of £1,000 to make their numerical values more similar to QALYs and facilitate estimation. The mixed model estimates the intervention effects on total yearly costs and QALYs; these are discounted and summed to give the discounted intervention effects on total costs and QALYs.
Table 3 presents the cost-effectiveness results. The mean differences in costs and QALYs and the incremental cost-effectiveness ratio changed according to the method. The difference in costs was £1,668 (95 % CI 1,142–2,194) for CCA, £1,305 (95 % CI 805–1,806) for MI and £1,338 (843–1,833) for the mixed model; the difference in QALYs adjusted for baseline EQ-5D was 0.301 (95 % CI 0.093–0.508) for CCA, 0.244 (95 % CI 0.052–0.437) for MI and 0.227 (95 % CI 0.031–0.422) for the mixed model. The standard errors are larger in the CCA, which reflects the smaller sample size. The mixed model has slightly larger standard errors than MI in the incremental QALYs, possibly because of the large number of parameters to estimate compared with the analysis model post-MI. The average incremental costs and QALYs in the CCA are greater than that estimated with the MI and mixed model, suggesting a bias that would be introduced if MCAR has been assumed. However, the three methods agree that surgery is the cost-effective alternative. Sensitivity analysis is useful here to determine which departures from MAR can alter the conclusions.
6.3 Stage 3: Sensitivity Analysis to the MAR Assumption
The method described in Sect. 5 for multiply imputing data under MNAR using the pattern mixture model is used for sensitivity analysis, because it can easily be implemented in any statistical software [39, 40]. Costs and QALYs are imputed under MAR and then shifted under four separate scenarios: (1) costs are increased by between 10 and 50 % in the first year and by 10 % in subsequent years in the surgery arm; (2) costs are increased as in (1) but in both arms; (3) QALYs are reduced by between 10 and 50 % in the first year and by 10 % in subsequent years in both arms; and (4) QALYs are reduced as in (3) but only in the surgery arm. These scenarios were judged of most interest after discussion with clinical experts.
Figure 3 plots the probability that surgery is cost effective at £20,000 per QALY gained against the assumed shift in costs and QALYs. Increasing costs or decreasing QALYs in individuals with missing data in both patient groups (scenarios 2 and 3) makes little difference to the results. Similarly, the probability of cost effectiveness is robust to increasing the costs for the individuals with missing data allocated to surgery (scenario 1). The probability changes considerably only when the QALYs of individuals with missing data allocated to surgery are decreased, so that the data are assumed MAR in the medical management arm (scenario 4). Nonetheless, surgery remains the intervention most likely to be cost effective even if imputed QALYs in year 1 are reduced by 50 %. The results suggest, therefore, that the positive cost-effectiveness profile of surgery is robust to plausible departures from MAR. In other studies, however, there may be information from the literature, from the clinical team or trial coordinators that suggests that individuals with missing data are likely to have experienced much worse outcomes. Another option is to formally elicit the opinion of the trial team in the form of informed priors to use as a probability distribution around the variation in costs and QALYs, either in a pattern mixture or in a selection model framework. In any case, it is essential to discuss the findings of the sensitivity analysis with the trial team to ascertain the implications of its results to the overall conclusions of the study.
Sensitivity analysis: data are missing not at random for QALYs or for costs. Note—imputed costs between year 2 and 5 are increased by 10 %; imputed QALYs between year 2 and 5 are reduced by 10 %. The probability that surgery is cost effective is stable at values close to 1 even if the imputed costs are increased only for the individuals with missing data randomised to the surgery group. Changes in imputed QALYs have an impact on the probability of cost effectiveness if the shift is implemented only in patients with missing data randomised to the surgery group but probability remains above 50 % throughout all scenarios. QALY quality-adjusted life-year
7 Implications for Practice and Research
This is the first study to provide a structured approach and practical guidance on how to handle missing data on costs and health outcomes in the context of within-trial CEAs focusing on methods that are straightforward to implement but ensure unbiased results and make efficient use of the data. This study critically appraises these methods and highlights the key considerations for within-trial CEAs in the presence of missing data. In addition, it uses the principles proposed for the analysis of RCTs to provide a structured approach and practical recommendations to handle missing data in the context of within-trial CEAs, namely (i) how to choose a plausible assumption about the missing data mechanism; (ii) how to conduct the analysis under that assumption; and (iii) how to conduct sensitivity analysis to test the impact of alternative assumptions. This structured approach is illustrated with a case study, for which Stata® code is provided. The code should assist analysts to implement this approach in their analyses.
Table 4 summarises our recommendations for handling missing data in within-trial CEAs. These recommendations are based on current evidence and the authors’ experience in conducing within-trial CEAs and handling missing data. They complement existing best practice in the conduct and reporting of applied health economic evaluations [8–10], and are likely to change over time as the evidence base develops. Often, the most plausible and practical base-case assumption is that data are MAR. MAR can be implemented with a variety of methods. Three methods are reviewed (IPW, MI and likelihood-based methods) and the two appropriate methods for the case study (MI and likelihood-based methods) are applied. MI may be more attractive for within-trial CEA because the imputation model can include variables that are predictive of missingness, beyond those included in the analysis model (e.g. post-randomisation variables). Including these variables in the imputation model can reduce bias, increase precision and make more plausible assumptions about the reasons for the missing data than likelihood-based methods. MI is easier to implement when categories of cost data have different missing data patterns and therefore cannot be aggregated at overall cost level without loss of information. An additional advantage of MI is that it naturally extends to the sensitivity analysis using alternative assumptions about the missing data mechanism. Other ad hoc methods that cannot incorporate the uncertainty inherent in missing data and make implausible assumptions regarding the missing data mechanism (e.g. complete case, mean imputation or LVCF) should be avoided. The base-case assumption should be tested in the sensitivity analysis to assess how departures from MAR affect the results.
The objective was to provide guidance on the methods that are straightforward to apply to within-trial CEAs without advanced statistical knowledge. The selection of methods was based on the methods recommended for RCTs, methods explored in methodological papers and on the authors’ experience in the area [1–4, 30]. An exhaustive list of methods was beyond the scope, as well as methods for non-randomised studies. Other methods that ensure unbiased and efficient analysis of datasets with missing data are full-Bayesian analysis and doubly robust methods. Full-Bayesian analysis estimates the missing values and the parameters of interest (incremental costs, incremental QALYs) simultaneously [42]. Doubly robust methods, which combine two different methods such as IPW and a likelihood-based model for the outcome, ensure unbiased estimates as long as one of the models is correctly specified [43]. Both are complex to implement and mostly the subject of methodological research. A simple method for sensitivity analysis was exemplified and showed that the results were robust to departures from MAR. More sophisticated approaches (e.g. selection models) would require a better understanding of the possible MNAR mechanisms.
This practical guide has identified a few avenues for further research. The main evidence gap is in the relative performance of MI-MICE, MI-JM and likelihood-based models in handling the complex distributions and correlations of CEA outcomes and how best to implement them. This relates to the appropriate level of aggregation for CEA outcomes, handling non-normality and methods for model validation. Another area for research is in the methods for sensitivity analysis to the assumption on the missing data mechanism. The case study illustrated a simple approach to sensitivity analysis that tests the impact of assuming worse outcomes than predicted for individuals with missing data. Although pattern mixture and selection models can explicitly model alternative MNAR mechanisms, they are difficult to implement in practice. More research is warranted on practical approaches for sensitivity analyses and on the development of software tools to assist in their implementation.
References
Panel on Handling Missing Data in Clinical Trials; National Research Council. The prevention and treatment of missing data in clinical trials. Washington, DC: The National Academies Press; 2010.
Manca A, Palmer S. Handling missing data in patient-level cost-effectiveness analysis alongside randomised clinical trials. Appl Health Econ Health Policy. 2005;4(2):65–75.
Oostenbrink JB, Al MJ. The analysis of incomplete cost data due to dropout. Health Econ. 2005;14(8):763–76.
Briggs A, Clark T, Wolstenholme J, Clarke P. Missing…. presumed at random: cost-analysis of incomplete data. Health Econ. 2003;12(5):377–92.
Blough DK, Ramsey S, Sullivan SD, Yusen R. The impact of using different imputation methods for missing quality of life scores on the estimation of the cost-effectiveness of lung-volume-reduction surgery. Health Econ. 2009;18(1):91–101.
Fielding S, Fayers PM, McDonald A, McPherson G, Campbell MK. Simple imputation methods were inadequate for missing not at random (MNAR) quality of life data. Health Qual Life Outcomes. 2008;6(57):1–57.
Noble SM, Hollingworth W, Tilling K. Missing data in trial-based cost-effectiveness analysis: the current state of play. Health Econ. 2012;21(2):187–200.
Drummond M, Jefferson T. Guidelines for authors and peer reviewers of economic submissions to the BMJ. The BMJ Economic Evaluation Working Party. BMJ. 1996;313(7052):275–6.
National Institute for Health and Care Excellence. Guide to the methods of technology appraisal 2013. London: National Institute for Health and Clinical Excellence; 2013 Apr 4.
Ramsey S, Willke R, Briggs A, Brown R, Buxton M, Chawla A, et al. Good research practices for cost-effectiveness analysis alongside clinical trials: the ISPOR RCT-CEA Task Force Report. Value Health. 2005;8(5):521–33.
White IR, Horton NJ, Carpenter J. Strategy for intention to treat analysis in randomised trials with missing outcome data. BMJ. 2011;342:d40.
Little RJ, Rubin DB. Statistical analysis with missing data. New York: Wiley; 1987.
Little RJ. Modeling the drop-out mechanism in repeated-measures studies. J Am Stat Assoc. 1995;90(431):1112–21.
White IR, Thompson SG. Adjusting for partially missing baseline measurements in randomized trials. Stat Med. 2005;24(7):993–1007.
Seaman SR, Bartlett JW, White IR. Multiple imputation of missing covariates with non-linear effects and interactions: an evaluation of statistical methods. BMC Med Res Methodol. 2012;12(1):46.
Willan AR, Lin D, Manca A. Regression methods for cost-effectiveness analysis with censored data. Stat Med. 2005;24(1):131–45.
Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61(4):962–73.
Seaman SR, White IR. Review of inverse probability weighting for dealing with missing data. Stat Methods Med Res. 2013;22(3):278–95.
Molenberghs G, Thijs H, Jansen I, Beunckens C, Kenward MG, Mallinckrodt C, et al. Analyzing incomplete longitudinal clinical trial data. Biostatistics. 2004;5(3):445–64.
White IR, Royston P, Wood AM. Multiple imputation using chained equations: issues and guidance for practice. Stat Med. 2011;30(4):377–99.
Schafer JL. Analysis of incomplete multivariate data. Boca Raton: CRC Press; 2010.
Gomes M, Díaz-Ordaz K, Grieve R, Kenward MG. Multiple imputation methods for handling missing data in cost-effectiveness analyses that use data from hierarchical studies: an application to cluster randomized trials. Med Decis Mak. 2013;33(8):1051–63.
Lee KJ, Carlin JB. Multiple imputation for missing data: fully conditional specification versus multivariate normal imputation. Am J Epidemiol. 2010;171(5):624–32.
Van Buuren S. Multiple imputation of discrete and continuous data by fully conditional specification. Stat Methods Med Res. 2007;16(3):219–42.
Royston P. Multiple imputation of missing values: further update of ice, with an emphasis on categorical variables. Stata J. 2009;9(3):466.
Lambert PC, Billingham LJ, Cooper NJ, Sutton AJ, Abrams KR. Estimating the cost-effectiveness of an intervention in a clinical trial when partial cost information is available: a Bayesian approach. Health Econ. 2008;17(1):67–81.
Simons C, Rivero-Arias O, Yu L-M, Simon J. Missing data in the health related quality of life EQ-5D-3L instrument—should we impute individual domains or the actual index? Research paper presented at the 83rd Health Economists’ Study Group Meeting. 26th to 28th June 2013. Hosted by University of Warwick.
Duan N. Smearing estimate: a nonparametric retransformation method. J Am Stat Assoc. 1983;78(383):605–10.
Little RJ. Missing-data adjustments in large surveys. J Bus Econ Stat. 1988;6(3):287–96.
Burton A, Billingham LJ, Bryan S. Cost-effectiveness in clinical trials: using multiple imputation to deal with incomplete cost data. Clin Trials. 2007;4(2):154–61.
Schafer JL, Olsen MK. Modeling and imputation of semicontinuous survey variables. In: Proceedings of the Federal Committee on Statistical Methodology Research Conference; 1999; pp. 565–74. http://www.fcsm.gov/99papers/shaffcsm.pdf. Accessed 10 Jul 2014.
Abayomi K, Gelman A, Levy M. Diagnostics for multivariate imputations. J Royal Stat Soc: Ser C (Appl Stat). 2008;57(3):273–91.
Buuren S, Groothuis-Oudshoorn K. MICE: Multivariate imputation by chained equations in R. J Stat Softw. 2011;45(3):1–67.
Willan AR, Briggs AH, Hoch JS. Regression methods for covariate adjustment and subgroup analysis for non-censored cost-effectiveness data. Health Econ. 2004;13(5):461–75.
Efron B. Missing data, imputation, and the bootstrap. J Am Stat Assoc. 1994;89(426):463–75.
Verbeke G, Fieuws S, Molenberghs G, Davidian M. The analysis of multivariate longitudinal data: a review. Stat Methods Med Res. 2014;23(1):42–59.
Mason A, Richardson S, Plewis I, Best N. Strategy for modelling non-random missing data mechanisms in observational studies using Bayesian methods. J Off Stat. 2012;28(2):279–302.
Carpenter JR, Kenward MG, White IR. Sensitivity analysis after multiple imputation under missing at random: a weighting approach. Stat Methods Med Res. 2007;16(3):259–75.
Ratitch B, O’Kelly M, Tosiello R. Missing data in clinical trials: from clinical assumptions to statistical analysis using pattern mixture models. Pharmaceutical statistics. 2013;12(6):337–47.
Van Buuren S, Boshuizen HC, Knook DL. Multiple imputation of missing blood pressure covariates in survival analysis. Stat Med. 1999;18(6):681–94.
Grant A, Boachie C, Cotton S, Faria R, Bojke L, Epstein D, et al.; REFLUX Trial Group. Clinical and economic evaluation of laparoscopic surgery compared with medical management for gastro-oesophageal reflux disease—five-year follow-up of multicentre randomised trial (the REFLUX trial). Health Technol Assess. 2013;17(22):1–167.
Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis. 3rd ed. Boca Raton: CRC Press; 2014.
Vansteelandt S, Carpenter J, Kenward MG. Analysis of incomplete data using inverse probability weighting and doubly robust estimators. Methodol Eur J Res Methods Behav Soc Sci. 2010;6(1):37–48.
Acknowledgments
The authors would like to thank Professor Adrian Grant and the team at the University of Aberdeen (Professor Craig Ramsay, Janice Cruden, Charles Boachie, Professor Marion Campbell and Seonaidh Cotton) who kindly allowed the REFLUX dataset to be used for this work, and Eldon Spackman for kindly sharing the Stata® code for calculating the probability that an intervention is cost effective following MI. The authors are grateful to the reviewers for their comments, which greatly improved this paper. M.G. is recipient of a Medical Research Council Early Career Fellowship in Economics of Health (grant number: MR/K02177X/1). I.R.W. was supported by the Medical Research Council [Unit Programme U105260558]. No specific funding was obtained to produce this paper. The authors declare no conflicts of interest.
Authors’ contributions
All authors contributed to the conception, the design and drafting of the paper. R.F. conducted the analysis and drafted the first and subsequent versions of this paper, with input from M.G., D.E. and I.R.W. All authors reviewed and approved the final paper. R.F. is the guarantor for the overall content.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Faria, R., Gomes, M., Epstein, D. et al. A Guide to Handling Missing Data in Cost-Effectiveness Analysis Conducted Within Randomised Controlled Trials. PharmacoEconomics 32, 1157–1170 (2014). https://doi.org/10.1007/s40273-014-0193-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40273-014-0193-3