Abstract
Introduction
Intravenous lipid emulsions (ILE) have been credited for successful resuscitation in drug intoxication cases where other cardiac life-support methods have failed. However, inter-individual variability can function as a confounder that challenges our ability to define the scope of efficacy for lipid interventions, particularly as relevant data are scarce. To address this challenge, we developed a quantitative systems pharmacology model to predict outcome variability and shed light on causal mechanisms in a virtual population of rats subjected to bupivacaine toxicity and ILE intervention.
Materials and Methods
We combined a physiologically based pharmacokinetic–pharmacodynamic model with data from a small study in Sprague-Dawley rats to characterize individual-specific cardiac responses to lipid infusion. We used the resulting individual parameter estimates to posit a population distribution of responses to lipid infusion. On that basis, we constructed a large virtual population of rats (N = 10,000) undergoing lipid therapy following bupivacaine cardiotoxicity.
Results
Using unsupervised clustering to assign resuscitation endpoints, our simulations predicted that treatment with a 30% lipid emulsion increases bupivacaine median lethal dose (LD50) by 46% when compared with a simulated control fluid. Prior experimental findings indicated an LD50 increase of 48%. Causal analysis of the population data suggested that muscle accumulation rather than liver accumulation of bupivacaine drives survival outcomes.
Conclusion
Our results represent a successful prediction of complex, dynamic physiological outcomes over a virtual population. Despite being informed by very limited data, our mechanistic model predicted a plausible range of treatment outcomes that accurately predicts changes in LD50 when extrapolated to putatively toxic doses of bupivacaine. Furthermore, causal analysis of the predicted survival outcomes indicated a critical synergy between scavenging and direct cardiotonic mechanisms of ILE action.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
We quantified variability of cardiac responses to lipid emulsion infusions by estimating individualized parameters for a pharmacokinetic–pharmacodynamic model applied to rats. |
We used the variability observed across a small population to simulate a large virtual population experiencing bupivacaine systemic toxicity followed by an intravenous lipid intervention. |
We thereby demonstrated that a predictive virtual population model for lipid emulsion therapy can be developed by integrating very limited physiological data with mechanistic physiologically based pharmacokinetic modeling. Median lethal dose predictions for treated versus untreated bupivacaine toxicity agreed well with prior experimental observations, and causal analysis supported a key role being played by accumulation of bupivacaine in muscle tissue rather than the liver. |
1 Introduction
Over the 2 decades since lipid resuscitation was first proposed [2], researchers have used in vitro [3,4,5] and in vivo [2, 4, 6,7,8,9,10,11,12,13,14,15,16] experiments, clinical case reports [17, 18], and systematic reviews [19,20,21,22,23,24] to explore the value of intravenous lipid emulsions (ILE) as an antidote for drug toxicity. For the case of local anesthetic toxicity, committees developed guidelines and recommendations based largely on animal models and without formalized clinical trials [25,26,27]. In silico methods have emerged as an additional approach to examine the therapeutic implications of the hypothesized pharmacokinetic (PK) and cardioactive functions of intravenous (IV) emulsions [6,7,8, 28]. Independent computational and integrative computational/experimental studies have revealed the limitations of the proposed ‘lipid sink’ mechanism of toxin sequestration as a sole driver of toxicity reversal. Instead, the field has recast the lipid sink (or scavenging) as just one part of a more complex, multifunctional picture of lipid resuscitation [7, 8, 25]. Resuscitation is now thought to depend heavily on a direct stimulation of cardiac contractility via at least two routes: the Frank-Starling mechanism common to all fluid resuscitation and an as yet unclear direct cardiotonic impact of IV fats on the heart. Similar mathematical models could serve to enrich empirical studies by generating mechanistic predictions about non-heuristic physiological outcomes when key toxicity and treatment variables are perturbed. Furthermore, by incorporating statistical variability into a deterministic mechanistic model, a validated mathematical model can be extended to account for inter-individual variability across populations.
The aim of this study was to determine whether the scarce in vivo data typical of lipid resuscitation studies is sufficient to inform a predictive virtual population model of ILE-mediated toxicity reversal. The modeling framework is a physiologically based pharmacokinetic–pharmacodynamic model (PBPK-PD). Beginning with data from a prior small study in rats [1], we used PBPK-PD modeling to construct a large (N = 10,000) virtual population undergoing ILE therapy after simulated bupivacaine administration. Based on this virtual population, we simulated a plausible range of treatment outcomes that accurately predicted changes in median lethal dose (LD50) when extrapolated to putatively toxic doses of bupivacaine. Using causal analysis, we have also demonstrated that the PBPK-PD predictions are consistent with muscle accumulation of bupivacaine acting as a driver of survival outcomes and liver accumulation being a consequence—rather than a cause—of survival. Furthermore, our virtual population data indicates that the efficacy of lipid therapy depends on a critical synergy between scavenging and direct cardiotonic mechanisms of action. This effort serves as a proof-of-concept that virtual population PBPK models informed by small experimental studies can support quantitative assessments of the potential of lipid therapy.
2 Methods
2.1 Model Description
2.1.1 Pharmacokinetic–Pharmacodynamic Model
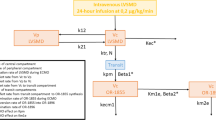
We have built upon a PBPK model of bupivacaine disposition in humans [28] and a PBPK-PD model describing its cardiotoxic effect in rats [7]. These models account for the distribution, metabolism, and elimination properties of bupivacaine and a lipid emulsion, as well as interactions between the anesthetic and emulsion. We modeled the pharmacodynamic (PD) effects of bupivacaine and ILE on cardiac function using maximal effect functions of the Hill form (Eqs. 1a, 1b, respectively). A linear function represents the positive inotropic effect of excess fluid volume, Evol, as proportional to the fractional increase in venous return (Eq. 1c).
Note that the depressive effect of bupivacaine, Ebup, depends on the concentration of the anesthetic in the cardiac tissue (Cbup,tis), while the cardiotonic effect of lipid, Elip, depends on the triglyceride concentration in the blood plasma (Clip,plasma), with β and n functioning as Hill constants. Cu,bup is the unbound concentration of bupivacaine in plasma within the heart, which acts as a non-competitive inhibitor of the lipid cardiotonic effect [8, 29]. KI is the inhibition constant, which is equal to the ion-channel dissociation constant of bupivacaine (KI = 0.9 μM). Kvolume is a proportionality constant, while the ratio of Qv to Qb is that of the return venous blood flow rate to the baseline flow rate. We described cardiovascular response to these three factors using the differential algebraic system in Eqs. (2a, 2b).
U in Eq. (2a) represents the proportional feedback control signal for homeostasis. QCO and Qb represent the time-dependent cardiac output and the baseline cardiac output, respectively. As the blood flow rates that drive drug and lipid distribution in the PBPK model scale with cardiac output—and drug and lipid distribution, in turn, alter cardiac output—we must solve the PK and PD equations as a single, fully coupled, system of equations.
2.1.2 System-Specific Pharmacokinetic Parameters
We developed the original PBPK model for humans [28] and subsequently adapted the model to rats [7, 8]. For this study, we assigned system-specific physiological parameters to be characteristic of a male Sprague-Dawley rat [30]. For our virtual population, we then scaled organ volumes and baseline blood-flow rates according to body weight, which we represented as log-normally distributed with mean of 350 g and standard deviation of 35 g (median 350 g, 95% confidence interval [CI] 290–420).
2.1.3 Plasma-Tissue Partitioning and Plasma Protein Binding
We estimated plasma-tissue and plasma-red blood cell partition coefficients for bupivacaine using the mechanistic model of Rodgers et al. [31]. Our PBPK model represents plasma protein binding as a concentration-dependent phenomenon by adopting the two-component binding capacity and affinity parameters reported by Coyle et al. for bupivacaine binding in rat plasma [32]. Compared with the human model [28], we determined the fraction of bupivacaine bound to rat plasma proteins to be less concentration sensitive—varying from 94 to 97% for plasma concentrations up to 2 mM.
2.1.4 Hepatic Metabolism
We adopted a well-stirred model for bupivacaine hepatic elimination and estimated an intrinsic unbound clearance (Clu,int) of 3.9 mL/s from the liver blood flowrate and the hepatic extraction ratio of 0.2 reported by Dennhardt et al. [33]). As with all other organs in the model, we have assumed the uptake of bupivacaine within the liver to be perfusion-limited, and we have treated the unbound concentration in plasma as indicative of the unbound concentration in extracellular water. Taking Clu,int to be representative of metabolic enzyme kinetics in the limit of low drug concentration (i.e., Clu,int = Vm/Km), we estimated a maximum metabolic rate of 0.0737 μmol/s based on the saturation constant of Km = 25.4 μM observed for rat liver hepatocytes in vitro [34]. We then captured hepatic metabolism of bupivacaine in our model using a saturable Michaelis–Menten formulation.
2.1.5 Lipid Pharmacokinetics
We treated plasma triglyceride volume (Vlip,plasma), as an explicit state variable in the model. Likewise, the triglyceride content of the administered intravenous fluid was an explicit parameter. Thus, we modeled the specific ILE formulation (concentration) of interest by setting the correct volume fraction for triglycerides in the administered fluid. The PBPK model then tracked total fluid volume and triglyceride volume using individual material balance equations.
2.2 Experimental Data
The data we used for this analysis originated in a study performed by Fettiplace et al. [1] investigating the effect of lipid infusion on cardiac function in healthy rats. The authors continuously monitored cardiac output while each animal received an intravenous dose of a 20% lipid emulsion at a rate of 9 mL/kg/min for 1 min. Their data spans a period of 9 min following the initiation of ILE infusion (Fig. 1A). Since only lipid was administered, the PD parameters that we can potentially estimate from these datasets are those in Eqs. (1b) and (1c), as summarized in Table 1.
A Aortic flow rate (normalized relative to baseline) following a lipid infusion of 20% lipid emulsion at 9 mL/kg/min for 1 min. Data from Fettiplace et al. [1], representing seven different observations from N = 6 Sprague Dawley rats. B Normalized standard error associated with estimating subsets of the model parameters. See Table 1 for list of parameters
2.3 Statistical Approach: Parameter Estimation and Model Selection
We used an ordinary least squares approach for parameter estimation [35,36,37,38]. Our goal was to estimate the parameter set \(\left( \theta \right)\) that minimizes the ordinary least squares (OLS) objective describing the difference between model-predicted cardiac output (\(f\left( {t_{i} ,\theta } \right)\)) and the observed cardiac output (yi) at each timepoint (ti) (Eq. 3).
We used ode15s in MATLAB to numerically integrate the differential equations in our model and used lsqnonlin in MATLAB to find parameter values that minimized the OLS objective. We calculated an initial estimate for the optimal parameter values by using the direct search global optimization algorithm [39], which avoids the likelihood of becoming trapped in a local minimum surrounding these initial estimates.
2.3.1 Uncertainty Quantification and Subset Selection: Which Model Parameters Can Be Estimated For Each Individual Dataset?
We limited our individual-specific parameter estimation to those parameters from Table 1 that could be reliably estimated from the available experimental data. Reliability, in this context, requires that the normalized standard error (NSE) associated with each parameter estimate be less than an appropriately defined threshold. To determine the NSEs, we estimated all six candidate parameters for each ILE response dataset. We then used the complex step method [40] to estimate model sensitivity for each parameter. From the sensitivities, we approximated parameter covariances and standard errors [41,42,43].
To avoid the pitfall of overfitting due to having too many parameters in the model, we selected a subset of candidate parameters and estimated the standard errors for estimates of each—assuming that parameters beyond the subset are held constant. NSEs were normalized by dividing by the respective parameter estimates. We then discriminated between high-confidence and low-confidence estimates by comparing NSE to the value 1/1.96, a limit that ensures that the lower bound of a 95% confidence interval for the associated parameter will be positive. In our model, negative parameter values would not be physiologically sound. We repeated this process for every possible parameter subset (63 total) and selected the subset that yielded the greatest number of parameters with normalized standard errors below the acceptance threshold.
2.3.2 Allowing Selected Parameters to Vary With Time
We approximated potential temporal variation in the selected parameters by treating them as piecewise, continuous functions of time (i.e., linear splines) [44]. Each parameter was then no longer represented by a single value, but rather by m + 1 variables, each describing the value of the parameter at a particular transition point in time. The result was a time-dependent representation of the parameter value by m piecewise linear functions. We incorporated spline functions of this type into our model for each parameter that was found to have high confidence by subset selection (see Sect. 2.3.1). Thus, we increased our total number of model parameters by pm (where p is the number of parameters in the selected subset). To characterize the trade-off between model performance and model complexity, we investigated spline approximations with m = 1, m = 4, and m = 8 (i.e., 2, 5, or 9 nodes). We selected these values so that the splines could be progressively nested each time m was increased, allowing us to perform the model comparison tests described in the following section.
2.3.3 Selecting the Most Appropriate Model
Model selection aims to identify, from a pool of candidates, the model variant that provides the best fit to data while avoiding unnecessary complexity and overfitting. We used comparison tests to quantitatively assess whether increasing the number of model parameters by introducing additional spline nodes improved the model quality. One statistical metric for quantitatively comparing models is the Akaike Information Criterion (AIC) [35]. Models with lower AIC scores are considered more appropriate to describe the data in question. A drawback of relying solely upon AIC is that the difference between two scores does not directly translate to a statement of statistical significance. We therefore supplemented our model selection procedure with model comparison nested restraint tests [45, 46]. This approach assumes that a model with fewer parameters can be recovered from a model with more parameters simply by holding some of the parameters in the latter constant (i.e., the models are effectively 'nested' within each other). With this framing, we can generate a test statistic to determine whether the model is significantly improved by estimating the nested parameters. We used these tests in conjunction with AIC scores to (1) determine which of the parameters identified by subset selection should be treated as time varying and (2) establish the number of splines sufficient to represent them.
2.4 Simulating Large Virtual Populations
Having estimated parameter values for each individual dataset, we defined population distributions of the associated PD characteristics and parameterized these according to our in vivo sample of N = 7. We then constructed a virtual population of rats (N = 10,000), each of whose physiological characteristics were determined by random sampling from the parameter population distributions. Based on an observed skew in the distribution of our estimated parameter values, we elected to treat our PD response parameters as log-normally distributed across the subject population.
We employed this virtual population to assess outcomes during simulated ILE therapy following local anesthetic systemic toxicity. We modeled bupivacaine overdose as a 10 mg/kg infusion administered at a constant rate for 20 s. This is in keeping with the work of Fettiplace et al. [7, 8], in which this dose allowed for cardiac depression with intervention-free spontaneous recovery. We then simulated treatment with an ILE infusion beginning 30 s after completion of the bupivacaine dose. To reflect lipid dosing that is known to successfully drive rapid reversal of toxicity [7], we simulated a treatment regimen consisting of 4 mL/kg of a 30% ILE formulation administered over 60 s. Our simulations predicted the time-dependent cardiac output for each of the virtual rats. We then used these 10,000 realizations to assess the predicted therapeutic impact of ILE interventions across a broad population.
2.4.1 Accounting for Variations in Sensitivity to Bupivacaine
Ideally, we would have also simulated a population distribution for the model parameters describing bupivacaine toxicity (i.e., those in Eq. 1a). This was not possible with available experimental datasets, but prior work has demonstrated considerable inter-individual variability in bupivacaine sensitivity. For example, Mauch et al. noted a 50% depression of mean arterial pressure requiring between 5 and 20 mg/kg doses in piglets [47]. To probe the potential implications of differences in bupivacaine sensitivity, we created an additional dimension of variability for our virtual population by introducing random variation in parameters EC50,bup and β. We sampled each parameter from a normal distribution with a mean equal to its respective population estimate and standard deviation equal to 10% of the mean. These distribution parameters yielded a virtual population in which 90% of individuals spontaneously recovered ≥ 30% of baseline cardiac output by t = 7 min—mimicking the experimental observation that a 10-mg/kg bolus of bupivacaine delivered to Sprague Dawley rats over 20 s causes cardiovascular toxicity that resolves spontaneously [7, 8].
2.4.2 Determining Survival Outcomes for Elevated Doses of Bupivacaine
Next, we extrapolated the model to the setting of elevated toxicity by simulating bupivacaine doses of 15, 20, 25, and 30 mg/kg. These are doses that are known to yield cardiac arrest that requires resuscitation (fluid intervention with or without CPR). Along with the 10 mg/kg virtual population, considering outcomes in the absence of a fluid intervention or with treatments of saline, 10% ILE, 20% ILE, and 30% ILE, this amounts to 250,000 virtual rats.
To determine a mortality fraction corresponding to each bupivacaine dose, we assigned the predicted PBPK-PD dynamics to death or survival endpoints by performing unsupervised clustering of the simulated data using a Gaussian mixture model [48, 49]. We used the following 17 features for classification: area under the curve and area under the first moment of the curve for cardiac output; area under the curve and area under the first moment of the curve for bupivacaine concentration in heart, brain, liver, adipose, and muscle tissues; dynamic time warping distance between curves for cardiac output in each individual and curves representing the 2.5% and 97.5% quantiles of cardiac output in the 10-mg/kg dataset; plasma bupivacaine distribution half-life; area under the curve and area under the first moment of the curve for the lipid concentration in arterial plasma. Prior to fitting the mixture model, we transformed these features by min–max scaling and principal component analysis. We identified the cluster corresponding to fatal overdose as the one whose population increased monotonically with increasing bupivacaine dosage and decreased monotonically with fluid interventions of increasing lipid concentration.
2.4.3 Causal Analysis of PK Outcomes
To clarify the possible causal relationship between bupivacaine PK, plasma lipid PK, and survival, we examined our data through the lens of candidate structural causal models [50, 51]. To discriminate between plausible and implausible causal models, we first generated network graphs to visualize the feature correlations present in our data when controlling for treatment (Tx) and dose. We then assessed the changes that occurred when we controlled for survival (the outcome of interest) in data already stratified by bupivacaine dose and treatment (exposures of interest). By examining the conditional independencies suggested by candidate structural causal models (using DAGitty [52]), we determined which PK phenomena appear to drive survival outcomes. We also determined the average causal effect (ACE; Eq. 4) of the emulsion’s scavenging and direct cardiotonic mechanisms on probability of survival. For that purpose, we considered 15 populations of virtual rats, with 10,000 members each, receiving bupivacaine doses of 10, 15, 20, 25, or 30 mg/kg, followed by a fluid infusion acting by a volume effect alone or one that acts by volume coupled with scavenging or direct cardiotonic mechanisms. The lipid concentration assigned to the latter two cases was 30%.
3 Results
3.1 Determining Which Model Parameters to Estimate at the Individual Level
In Fig. 1B, we present the results of parameter subset selection for one ILE response dataset. Here, and for all seven datasets, the consistent consensus was that two model parameters may be estimated at the individual level: Emax and one of the control parameters (either α or kp). Since analysis of the off-diagonal entries of the covariance matrices demonstrated α and kp to be perfectly correlated, the choice between the two was inconsequential, and we arbitrarily selected kp. This result is unsurprising, as although kp and α have distinct physiological interpretations (governing the accumulation of a control signal vs sensitivity of cardiac output to that signal), mathematically, they appear as an unidentifiable product. We incorporated spline representations of Emax and kp into the PKPD model for estimation as temporally varying parameters, and we set the remaining parameters in Table 1 to their mean population estimates and held them fixed. Hereafter, we refer to our candidate models as Constant, mEmax, mkp, and mEmax/kp, where m represents the number of splines used to describe time-varying parameters (either 1, 4, or 8) and Emax, kp, and Emax/kp denote which parameters we selected for time variance (as opposed to treating them as constants).
3.2 Selecting Time-Varying Parameters and Most Appropriate Model
Representing selected parameters as time-varying improved the ability of the model to capture the multiple maxima observed in the experimental data. We also observed improved tracking of the initial peak in cardiac output (Fig. 2A), with the greatest improvement in fit to the data observed when we increased the number of splines from m = 4 to m = 8. AIC scores likewise indicated an improvement in model quality when the model used eight splines (Fig. 2B), and we observed the lowest AIC score for the model in which Emax was represented as time-varying, while kp was held constant. This held true for all seven datasets and across all nested model comparisons (Fig. 2D). Thus, we selected the PD model with Emax represented as time-varying via eight splines. While we considered models with more than eight splines, there was no additional benefit from adding more nodes, as indicated by increased AIC scores and p values > 0.05 in model comparison tests.
Model selection. A Sample fits for the constant value and time-dependent parameter (m = 8 splines) models. B AIC scores assessing relative model quality as a function of the number of nodes used for spline representation of time-dependent parameters. Figure legend indicates which parameters are time dependent in the evaluated model. C Distribution of time-dependent Emax values for the N = 7 datasets at each of the estimated nodes. D Test statistic for the hypothesis that the reference model indicated in the table is superior to the nested model used for comparison testing. Bars indicate the number of individual datasets for which the reference model is an improvement over the nested model. Markers show the mean p value for the model comparison tests across all seven datasets. Where p > 0.05, the more complex reference model is not taken to be an improvement over the simpler, nested model, despite a reduced cost function. In the model labels, constant implies no temporal variation, m represents the number of splines used to describe time-varying parameters, and Emax, kp, and Emax/kp denote which parameters are time-varying. AIC Akaike information criterion, Emax maximum effect of lipid on cardiac function, kp proportional control constant for homeostasis, OLS ordinary least squares cost
The time-dependent value of Emax exhibits a consistent trend across all seven datasets, declining over time (Fig. 2C). In all cases but one, Emax takes its peak value within the first 5 min after lipid administration. We observed the greatest variability across the group at early times (t = 0 min: μ = 9.4, σ = 9.0, γ = 1.6), with the distribution of values becoming symmetric and narrower with time (at t = 8 min: μ = 1.5, σ = 1.1, γ = −0.035). For time-independent parameter kp, the population distribution exhibited positive skew, with μ = 1.1, σ = 1.9, γ = 1.3.
3.3 Predictions for Virtual Populations
We generated physiological phenotypes for a virtual population of 10,000 rats by randomly sampling parameter values from lognormal functions fitted to the distributions indicated by the seven individualized models (i.e., one lognormal distribution for each of the nine nodes of Emax and one distribution for the time-invariant parameter kp). We sampled bupivacaine sensitivity parameters from a normal distribution, as described in the Methods section. Using this virtual population, we then simulated bupivacaine systemic toxicity and recovery with or without fluid intervention. We validated the bupivacaine PBPK model by comparing simulation outcomes to the experimental concentration-time data reported by Dennhardt et al. [33] and Fettiplace et al. [8], who report whole blood and cardiac tissue bupivacaine concentrations, respectively (Fig. S1).
3.3.1 For a Low Dose of Bupivacaine, Lipid Bolus Reduces Recovery Time, But Does Little to Change Variability Across the Population
In the absence of a simulated fluid intervention, rats exhibiting rapid recovery returned to ≥ 30% of baseline cardiac output by ~ 3 min, while those that recovered more slowly required ~ 7 min to do so (Fig. 3A). A 30% lipid intervention drove nearly the whole population to recover in < 4 min (Fig. 3D). As expected, these improved outcomes were associated with a reduction in bupivacaine content of cardiac tissue (Fig. 3B, E). We found the half-life describing washout of bupivacaine from cardiac tissue exhibited a lower median value, but similar range of variability, following lipid intervention (untreated half-life of 0.86 min, 95% CI 0.75–1.0; lipid treated half-life of 0.55 min, 95% CI 0.36–0.67). This phenomenon was also evident in the case of brain tissue (Fig. 3C, F), where a prolonged retention of anesthetic was curtailed by lipid. Unlike other rapidly perfused organs, the liver exhibits an increase in bupivacaine following lipid infusion (Fig. S3A & D, see electronic supplementary material [ESM]). This is because the bulk of the liver’s blood input is outflow from other rapidly perfused organs. When lipid uptake of bupivacaine augments removal of the anesthetic from the spleen, gut, and pancreas, the liver experiences an increased bupivacaine inflow. Lipid-carried bupivacaine also increases outflow of bupivacaine from the liver. However, the net effect is such that the bupivacaine concentration in the liver initially increases. In agreement with prior work [8], ILE initially induces an increase in muscle bupivacaine as well (Fig. S3C & F, see ESM). This effect was transient, and the PBPK model predicts accelerated redistribution ~ 1 min after lipid administration.
A–F Predicted time courses for cardiac output and bupivacaine content of vital organs. Each plot represents outcomes for a virtual population of 10,000 rats. Top row: spontaneous recovery (no fluid intervention). Bottom row: recovery following treatment with a 60 s bolus of 30% ILE at 4 mL/kg. A, D Recovery of cardiac output. B, E Bupivacaine in the heart. C, F Bupivacaine in the brain. Dark regions: 95% intervals. Light regions: 50% intervals. Solid black line: median. Vertical dashed lines indicate beginning and end of lipid administration. G Distribution half-lives quantified across the virtual population. Figure displays population distributions pairwise for total plasma (left-hand, darker violin plot) and unbound bupivacaine in plasma (right-hand, lighter violin plot). H Mortality curves for simulated resuscitation scenarios following bupivacaine bolus doses of 10, 15, 20 and 25 mg/kg. Each marker summarizes the predicted mortality outcomes for a virtual population of 10,000 rats. Lines indicate the sigmoid dose–response curves used to estimate the median lethal dose. ILE intravenous lipid emulsion
3.3.2 Based on Plasma PK, Drug Scavenging and Cardiotonic Mechanisms Play Partially Redundant Roles in Hastening Bupivacaine Redistribution
The plasma distribution half-life characterizes the initial rapid fall-off of bupivacaine in the blood plasma as the drug is delivered from the site of administration to the organs of the body. For total bupivacaine in arterial plasma (bound to blood proteins, associated with lipid, and unbound) and bupivacaine in its unbound state, we quantified distribution half-lives (τ½,D) as a function of posited mechanisms of ILE therapeutic action (Fig. 3G; Table S3, see ESM). We considered (1) the null case of no lipid intervention, (2) treatment with 30% ILE, (3) a hypothetical lipid-like infusion with no capability for bupivacaine sequestration (no scavenging), and (4) another hypothetical infusion with only a sequestration capability (i.e., no direct inotropic or metabolic effect). As the shape of the concentration–time curves varied from apparent two-component to three-component decays, or even exhibited ‘bumps’ that deviated from a smooth, convex behavior (Fig. S2), we chose to quantify half-lives by performing linear regressions on ln(C) versus t for a moving window of 10 s. We identified the smallest time constant (most rapid decay constant) as the distribution half-life for each virtual rat.
Simulated lipid therapy reduced the magnitude and range of τ½,D for total plasma bupivacaine by 36% and 82%, respectively. Scavenging or cardiotonic effects alone reduced τ½,D by 9% and 27%, respectively. The variation across the population was reduced by 53% and 60%, respectively. The impact on unbound bupivacaine was similar or greater, with median τ½,D reduced by 50%, 40%, and 50%, respectively (range reduced by 81%, 66%, and 77%, respectively). As the unbound concentration is the one most relevant to tissue exposure, these results suggest a partial redundancy of the scavenging and cardiotonic mechanisms as promoters of bupivacaine redistribution. As the pharmacodynamic spline parameters in our model do not describe responses beyond a 9-min window, we could not assess the potential impact of fluid interventions on systemic clearance.
3.3.3 Out-of-Sample Prediction of Mortality Fractions
In agreement with experimental observations, our simulations predicted that almost all virtual rats (98%) would survive the lowest anesthetic dose—with or without intervention (Fig. 3H). All rats were predicted to succumb to the 30-mg/kg dose, unless a fluid intervention was simulated. Predicted median lethal doses (LD50) were (median [95% CI]) 15.5 [15.3–15.8], 17.7 [17.2–18.1], 20.2 [20.0–20.4], 22.9 [22.5–23.4], and 25.7 [25.5–26.0] mg/kg, respectively, for the case of no fluid intervention (null), and equal-volume infusions of a control fluid infusion without lipid content, 10% ILE, 20% ILE, and 30% ILE. By inspecting feature distributions for the low-dose case of 10 mg/kg, we observed similar findings to those reported by Fettiplace et al. [8], viz ILE appearing to promote bupivacaine accumulation in liver while reducing cardiac bupivacaine exposure (Fig. S4A). Unlike in the prior study, our virtual population predicted a small reduction in muscle bupivacaine. Having distinguished between survivors and non-survivors in the high-dose virtual populations, we were able to assess whether these PK phenomena are associated with improved survival outcomes. Segregating our data by bupivacaine dose, we observed a pronounced association of survival with increased liver exposure to bupivacaine, with survivors exhibiting liver area under the concentration curve (AUC) ~ 70% greater than non-survivors (Fig. 4). In contrast, cardiac AUC was ~ 70% smaller for survivors than for non-survivors. Muscle AUC in survivors was ~ 10% greater. These findings were very similar for rats who were not subject to ILE intervention (Tx = null, saline; Fig. S4B), suggesting that these patterns are not unique to lipid intervention.
AUC histograms comparing survivors and non-survivors of bupivacaine overdose. Distributions represent data aggregated over 10% ILE, 20% ILE, and 30% ILE treatments. Survivors exhibit lower bupivacaine exposure in cardiac tissue and higher exposure in liver and muscle tissues. Kolmogorov-Smirnov tests suggest that all pairs of histograms exhibit statistically significant differences (p < 0.001). Orange: survivors, blue: non-survivors. AUC area under the concentration curve, ILE intravenous lipid emulsion
3.3.4 Causal Effect Analysis Clarifies Complex Dependence of Survival on Bupivacaine and Lipid PK
Given the partial mechanism redundancy suggested by the plasma bupivacaine PK analysis, we asked whether scavenging of the anesthetic is a significant contributor to survival. In Table S4, we report survival outcomes for simulated fluid infusions of varying lipid concentrations and mechanisms of action (see ESM). Treating the choice of therapeutic mechanism as an intervention [51], we determined the ACE of introducing a scavenging mechanism to be 16% and that of introducing a direct cardiotonic mechanism to be negligible. When combined, however, the two mechanisms confer a synergistic advantage, such that the 30% ILE increases the number of surviving rats by 39% when compared with an untreated bupivacaine overdose. In Table 2, we present further analysis of resuscitation outcomes as a function of emulsion concentration.
The ACE analysis reinforces that lipid treatment has a positive effect on resuscitation outcomes through multiple synergistic mechanisms. Further, increasing the lipid concentration increases that effect. However, when we inspected the relationship between survival probability (posterior probability of the virtual rat belonging to the survival cluster) and arterial lipid AUC, we observed a strong negative association (ρ = − 0.76; p < 0.001). This was true for all groups when stratified by bupivacaine dose and choice of treatment, so it is not a consequence of dose or treatment acting as confounders. Whereas no correlation appeared between heart and muscle bupivacaine AUC when survivors and non-survivors were aggregated (Fig. 5A), controlling for survival produced a moderate correlation between these PK features (ρ = 0.45; Fig. 5B). In contrast, controlling for survival substantially diminished the association that had existed between cardiac and liver AUC (reduced from ρ = − 0.54 to ρ = − 0.13). On this basis, we assigned heart and muscle AUC to be ancestors of survival that intersect via a collider. Conversely, we posited that liver and heart AUC likely interact with survival through a chain or fork path. Given the other associations evident in the network graphs, we proposed the structural causal model in Fig. 5C. By examining the testable implications (conditional independencies) suggested by analysis of this model using DAGitty [52] (Table S5, see ESM), we were able to confirm that the model is consistent with our virtual population data.
Feature correlations and proposed structural causal model for lipid resuscitation in virtual rats. Analysis includes bupivacaine doses of 15–30 mg/kg and all ILE treatment groups (10%, 20%, and 30%). A Graph depicting strength and direction of correlation between selected PK features. Nodes are the AUC features of interest and the probability of survival (i.e., likelihood of a rat being assigned to the survival cluster). Edges represent the existence of a correlation with p < 0.001 and ρ > 0.15. Line thickness indicates the strength of the correlation, and the line color indicates whether the correlation is positive (blue) or negative (purple). B The correlation graph that results from controlling for survival. C A plausible structural model indicating relationships between dose and treatment exposures, PK features, and population survival outcomes. Green arrows indicate causal paths. Blue nodes indicate ancestors of the outcome, and gray nodes are other variables that are not ancestors of the outcome. Diagram was produced and analyzed using DAGitty [52]. AUC area under the concentration curve, ILE intravenous lipid emulsion, PBPK-PD model physiologically based pharmacokinetic–pharmacodynamic model, PK pharmacokinetic
4 Discussion
4.1 Quality of Mortality Predictions
Using the exemplar of bupivacaine systemic toxicity and a PBPK-PD model in rats, we have demonstrated how limited physiological data can inform a model that predicts population outcomes of lipid therapy. The mortality fractions we have reported herein are computational predictions, and these have not been directly validated by experiment. However, they agree well with the findings of Weinberg et al. [2]. In their 1998 publication, they reported mortality data for N = 6 rats dosed with bupivacaine at 10–22.5 mg/kg over 10 s, prior to attempted resuscitation with 30% Intralipid™. They observed 0% mortality at a dose of 15 mg/kg when treated with Intralipid™ as a 30-s, 7.5-mL/kg bolus followed by an infusion of 3 mL/kg/min. Despite lipid intervention, 100% mortality was observed for the maximum dose of bupivacaine 22.5 mg/kg. Their small sample yielded an estimated LD50 of 18.5 mg/kg for resuscitation with 30% intralipid. Our simulations address a longer duration for bupivacaine administration (20 s). Thus, our estimated LD50 of 25.7 mg/kg is credible. Moreover, our simulations predict that treatment with 30% ILE increases bupivacaine LD50 by 46% when compared with a simulated control fluid. The corresponding increase reported by Weinberg et al. was 48%. It is important to note that no data from the prior study was used to inform our virtual population model. Our results represent a successful out-of-sample prediction of complex, dynamic physiological outcomes.
4.2 Causal Contributions of Pharmacokinetic and Pharmacodynamic Effects to Survival
Our prior work to uncover the mechanisms of lipid resuscitation considered bupivacaine doses low enough to produce transient cardiotoxicity from which rats could recover without intervention [7, 8]. Herein, we have taken that rat PBPK-PD model and extended it to the more pertinent scenario of potentially fatal bupivacaine overdose. We found that the prior findings held true in the distinct PK features identified for survival and fatal endpoints—namely, that survival after a bupivacaine overdose is associated with bupivacaine shifting away from the heart and into liver and muscle tissues. However, we observed this shift in all dose-treatment groups. It was not unique to ILE therapy and thus not tied specifically to a scavenging or cardiotonic mechanism of action. In fact, although the chance of survival was causally improved by selecting a lipid intervention of higher concentration, within a particular dose/Tx group, survival probability exhibited a negative correlation with plasma lipid AUC. However, the scavenging mechanism, which is driven by lipid droplets, was causally associated with improved survival outcomes. Plasma PK indicated some redundancy between scavenging and cardiotonic mechanisms, but a causal effect analysis comparing different therapeutic mechanisms confirmed that these effects are truly synergistic. Indeed, the therapeutic value of the cardiotonic effect was rendered negligible in the absence of scavenging. The inotropic impact of a fluid volume alone did promote bupivacaine washout from cardiac tissue, but—in the absence of scavenging—the impact appeared insufficient to relieve bupivacaine inhibition of the lipid cardiotonic effect.
By analyzing the PBPK-PD population data through the lens of a structural causal model, we clarified the relevance of bupivacaine and lipid PK in determining survival outcomes. Despite the modest shift in muscle AUC that appeared to distinguish survival and fatal endpoints following bupivacaine overdose, the causal model suggested that muscle accumulation of bupivacaine directly controls survival outcomes. Unsurprisingly, the same was true for cardiac accumulation of bupivacaine. The causal model highlighted cardiac output as a confounder of the interplay between survival and lipid accumulation in arterial plasma, with recovery of blood flow promoting survival but reducing arterial plasma lipid—presumably by driving its distribution throughout the vasculature and thereby increasing opportunities for lipase-mediated clearance. The model further indicated that, while liver AUC is a feature that correlates strongly with survival (ρ = 0.7; p < 0.001), it is a consequence rather than a direct effector of survival outcomes. This would seem to agree with prior experimental observations that augmented hepatic clearance of bupivacaine via the liver appears not to be required for hastened recovery [8].
4.3 Extension of This Modeling Framework to Other Cardiotoxins
Extension of this modeling approach to explore lipid therapy for other cardiotoxins, such as those associated with or implicated in enteral overdoses, should not require extensive experimental data. Our model is entirely mechanistic, with only a subset of the PD parameters needing to be obtained by fitting to in vivo data. We previously determined PD parameters for bupivacaine using data from an isolated heart study [53]. Others have quantified concentration-dependent lipid and protein binding of bupivacaine in vitro [3, 32], and we predicted plasma-tissue partitioning as a function of tissue composition and drug physicochemical properties using the mechanistic model of Rodgers et al. [31]. We then integrated the resulting mathematical relationships into a whole-body PBPK model, along with the in vivo data for lipid PD, to make population predictions about the impact of ILE therapy. Herein, bupivacaine functions as a canonical cardiotoxin for which prior data exist to inform this proof-of-concept modeling effort. If analogous in vitro, ex vivo, and limited PD data were available for other drugs of interest, one could extrapolate the modeling framework beyond the case of bupivacaine toxicity.
Given that key PD parameters will not be available for humans, we must always exercise care in extrapolating human dosage schedules from non-human models. However, incorporation of parameters reflecting species differences might allow investigators to explore how particular physiological phenomena could contribute to species differences in therapeutic effect. For example, incorporating human plasma protein binding parameters within our virtual rat model led to poor survival outcomes, even at low bupivacaine dose. The low capacity, high affinity binding protein in rat serum (α-1-acid glycoprotein) exhibits bupivacaine binding capacity 75% lower than that of human serum. The high capacity, low affinity binding protein in rat serum (serum albumin) exhibits binding capacity 79% greater than that of human serum [54]. Although binding affinities are similar between the two species, these differences in binding capacity cause human plasma to exhibit strongly concentration-dependent binding [28, 55]. The consequence is a fraction unbound in plasma that drops considerably with increased bupivacaine concentration, causing increased cardiac exposure to bupivacaine. While lipid still confers substantial benefit in virtual rats with human-like plasma (ACE = 40%), the window of efficacy narrows, with < 50% of the virtual population surviving a bupivacaine dose of > 15 mg/kg despite 30% ILE intervention.
4.4 Limitations
Our study has certain clear limitations, a key one being the fact that we have estimated parameter distributions from a sample of N = 7. We have also assumed that the range of PD responses observed in this sample can be extrapolated to rats with a broader range of body weights. For these reasons, the estimated parameter distributions may not be representative. Furthermore, our parameter subset selection procedure indicated that the experimental datasets did not offer sufficient information to estimate all six PD parameters with reasonable confidence. Of the three parameters we did not estimate (excluding α, which is perfectly correlated with kp), two contribute to the Hill equation for lipid-enhanced inotropy (EC50,lip and n), and the third describes the flow-promoting effect of increasing the fluid volume in the bloodstream (Kvolume). In retrospect, it is not surprising that we could not estimate Kvolume. Without data corresponding to a control infusion, we could not isolate the volume effect from the additional positive inotropic effect of the ILE. Indeed, the time-dependent behavior attributed to Emax may, in fact, be more properly associated with the volume effect. Alternatively, the time dependence of Emax may reflect a reverse use-dependence phenomenon, whereby the heart is more responsive to lipid when cardiac function is most compromised. Teasing apart the two inotropic mechanisms would require physiological data for a control fluid. Although we did not have access to the relevant data, the study performed by Fettiplace et al. [1] did report the outcomes of a control saline infusion. Including these data would likely permit estimation of Kvolume and its population distribution. Likewise, estimation of n and EC50 would be feasible if our dataset included multiple trials of the fluid infusion, with varied concentrations of lipid. We could then refine the model by revisiting the parameter estimation and accompanying statistical tests with the inclusion of the new data.
Fortunately, these limitations did not prevent us from achieving good fits via estimation of kp and Emax. The flexibility conferred by using time-varying parameters is apparent, as constant parameter values allowed the model to fit relatively smooth responses with a single peak, but irregular dynamics could not be captured. With the inclusion of eight splines for Emax, the model captured general trends without overfitting the noisy fluctuations present in the data. As kp is already involved in a time-varying equation, it is reasonable that little appears to be gained by describing its value as anything other than time-independent.
5 Conclusion
Using a PBPK model, we have characterized variable cardiac responses to lipid infusions in rats and used that information to develop a virtual population model of lipid resuscitation. Despite being informed by a very limited data set, this mechanistic model with relatively few tuning parameters plausibly predicted mortality outcomes across a range of bupivacaine doses. By acquiring similar data for other drugs of interest, this modeling approach could support exploration of lipid interventions without the need to involve large numbers of animals. Once validated, a virtual population model could be used to test alternative therapeutic regimens and develop approaches that achieve positive outcomes over a broad fraction of the population. This would be particularly helpful in determining how ILE administration might be altered to address oral overdoses, as heuristic extension of the guidelines for IV overdose has the potential to do harm rather than good [56]. The ability to build virtual populations from limited in vivo datasets would also make it more feasible to explore lipid interventions in more costly large animal models, where heart function more closely approximates human physiology.
References
Fettiplace MR, Ripper R, Lis K, Lin B, Lang J, Zider B, Wang J, Rubinstein I, Weinberg G. Rapid cardiotonic effects of lipid emulsion infusion. Crit Care Med. 2013. https://doi.org/10.1097/CCM.0b013e318287f874.
Weinberg GL, VadeBoncouer T, Ramaraju GA, Garcia-Amaro MF, Cwik MJ. Pretreatment or resuscitation with a lipid infusion shifts the dose-response to bupivacaine-induced asystole in rats. Anesthesiology. 1998;88(4):1071–5.
Mazoit JX, Le Guen R, Beloeil H, Benhamou D. Binding of long-lasting local anesthetics to lipid emulsions. Anesthesiology. 2009;110(2):380–6. https://doi.org/10.1097/ALN.0b013e318194b252.
Litonius E, Lokajova J, Yohannes G, Neuvonen PJ, Holopainen JM, Rosenberg PH, Wiedmer SK. In vitro and in vivo entrapment of bupivacaine by lipid dispersions. J Chromatogr A. 2012;1254:125–31. https://doi.org/10.1016/j.chroma.2012.07.013.
French D, Smollin C, Ruan W, Wong A, Drasner K, Wu AH. Partition constant and volume of distribution as predictors of clinical efficacy of lipid rescue for toxicological emergencies. Clin Toxicol (Phila). 2011;49(9):801–9. https://doi.org/10.3109/15563650.2011.617308.
Dureau P, Charbit B, Nicolas N, Benhamou D, Mazoit J. Effect of Intralipid® on the dose of ropivacaine or levobupivacaine tolerated by volunteers: a clinical and pharmacokinetic study. Anesthesiology. 2016;125(3):474–83. https://doi.org/10.1097/ALN.0000000000001230.
Fettiplace MR, Akpa BS, Ripper R, Zider B, Lang J, Rubinstein I, Weinberg G. Resuscitation with lipid emulsion: dose-dependent recovery from cardiac pharmacotoxicity requires a cardiotonic effect. Anesthesiology. 2014;120(4):915–25. https://doi.org/10.1097/ALN.0000000000000142.
Fettiplace MR, Lis K, Ripper R, Kowal K, Pichurko A, Vitello D, Rubinstein I, Schwartz D, Akpa BS, Weinberg G. Multi-modal contributions to detoxification of acute pharmacotoxicity by a triglyceride micro-emulsion. J Control Release. 2015;198:62–70. https://doi.org/10.1016/j.jconrel.2014.11.018.
Heinonen JA, Litonius E, Backman JT, Neuvonen PJ, Rosenberg PH. Intravenous lipid emulsion entraps amitriptyline into plasma and can lower its brain concentration—an experimental intoxication study in pigs. Basic Clin Pharmacol Toxicol. 2013;113(3):193–200. https://doi.org/10.1111/bcpt.12082.
Heinonen JA, Litonius E, Salmi T, Haasio J, Tarkkila P, Backman JT, Rosenberg PH. Intravenous lipid emulsion given to volunteers does not affect symptoms of lidocaine brain toxicity. Basic Clin Pharmacol Toxicol. 2015;116(4):378–83. https://doi.org/10.1111/bcpt.12321.
Heinonen J, Schramko A, Skrifvars M, Litonius E, Backman J, Mervaala E, Rosenberg P. The effects of intravenous lipid emulsion on hemodynamic recovery and myocardial cell mitochondrial function after bupivacaine toxicity in anesthetized pigs. Hum Exp Toxicol. 2017;36(4):365–75. https://doi.org/10.1177/0960327116650010.
Kimberly FM, Rachel GK, Sareh P, Ferrante SG, Stephane LB. Low dose Intralipid resuscitation improves survival compared to ClinOleic in propranolol overdose in rats. PLoS ONE. 2018;13(8):e0202871. https://doi.org/10.1371/journal.pone.0202871.
Litonius E, Niiya T, Neuvonen PJ, Rosenberg PH. No antidotal effect of intravenous lipid emulsion in experimental amitriptyline intoxication despite significant entrapment of amitriptyline. Basic Clin Pharmacol Toxicol. 2012;110(4):378–83. https://doi.org/10.1111/j.1742-7843.2011.00826.x.
Litonius ES, Niiya T, Neuvonen PJ, Rosenberg PH. Intravenous lipid emulsion only minimally influences bupivacaine and mepivacaine distribution in plasma and does not enhance recovery from intoxication in pigs. Anesth Analg. 2012;114(4):901–6. https://doi.org/10.1213/ANE.0b013e3182367a37.
Niiya T, Litonius E, Petaja L, Neuvonen PJ, Rosenberg PH. Intravenous lipid emulsion sequesters amiodarone in plasma and eliminates its hypotensive action in pigs. Ann Emerg Med. 2010;56(4):402-408.e2. https://doi.org/10.1016/j.annemergmed.2010.06.001.
Wong G, Pehora C, Crawford M. L-carnitine reduces susceptibility to bupivacaine-induced cardiotoxicity: an experimental study in rats. Can J Anesth/J Can Anesth. 2017;64(3):270–9. https://doi.org/10.1007/s12630-016-0797-5.
Meg AR, Mark A, Gregory WF, Chad JI, James BE. Successful use of a 20% lipid emulsion to resuscitate a patient after a presumed bupivacaine-related cardiac arrest. Anesthesiology. 2006;105(1):217–8. https://doi.org/10.1097/00000542-200607000-00033.
Sirianni AJ, Osterhoudt KC, Calello DP, Muller AA, Waterhouse MR, Goodkin MB, Weinberg GL, Henretig FM. Use of lipid emulsion in the resuscitation of a patient with prolonged cardiovascular collapse after overdose of bupropion and lamotrigine. Ann Emerg Med. 2008;51(4):412-415.e1. https://doi.org/10.1016/j.annemergmed.2007.06.004.
Zyoud SH, Waring WS, Al-Jabi SW, Sweileh WM, Rahhal B, Awang R. Intravenous lipid emulsion as an antidote for the treatment of acute poisoning: a bibliometric analysis of human and animal studies. Basic Clin Pharmacol Toxicol. 2016;119(5):512–9. https://doi.org/10.1111/bcpt.12609.
Hoegberg LCG, Bania TC, Lavergne V, Bailey B, Turgeon AF, Thomas SHL, Morris M, Miller-Nesbitt A, Megarbane B, Magder S, Gosselin S, Lipid Emulsion Workgroup. Systematic review of the effect of intravenous lipid emulsion therapy for local anesthetic toxicity. Clin Toxicol. 2016;54(3):167–93. https://doi.org/10.3109/15563650.2015.1121270.
Hayes BD, Gosselin S, Calello DP, Nacca N, Rollins CJ, Abourbih D, Morris M, Nesbitt-Miller A, Morais JA, Lavergne V. Systematic review of clinical adverse events reported after acute intravenous lipid emulsion administration. Clin Toxicol (Phila). 2016;54(5):365–404. https://doi.org/10.3109/15563650.2016.1151528.
Cao D, Heard K, Foran M, Koyfman A. Intravenous lipid emulsion in the emergency department: a systematic review of recent literature. J Emerg Med. 2015;48(3):387–97. https://doi.org/10.1016/j.jemermed.2014.10.009.
Cave G, Harvey M. Intravenous lipid emulsion as antidote beyond local anesthetic toxicity: a systematic review. Acad Emerg Med. 2009;16(9):815–24. https://doi.org/10.1111/j.1553-2712.2009.00499.x.
Fettiplace MR, Pichurko AB. Heterogeneity and bias in animal models of lipid emulsion therapy: a systematic review and meta-analysis. Clin Toxicol (Phila). 2021;59(1):1–11. https://doi.org/10.1080/15563650.2020.1814316.
Neal JM, Barrington MJ, Fettiplace MR, Gitman M, Memtsoudis SG, Mörwald EE, Rubin DS, Weinberg G. The third American Society of Regional Anesthesia and pain medicine practice advisory on local anesthetic systemic toxicity: executive summary 2017. Reg Anesth Pain Med. 2018;43(2):113–23. https://doi.org/10.1097/aap.0000000000000720.
Cave G, Harrop-Griffiths W, Harvey M, Meek T, Picard J, Short T, Weinberg G. Management of severe local anaesthetic toxicity. 2010. https://anaesthetists.org/Home/Resources-publications/Guidelines/Management-of-severe-local-anaesthetic-toxicity
Sophie G, Lotte CGH, Robert SH, Andis G, Christine MS, Simon HLT, Samuel JS, Bryan DH, Michael L, Martin M, Andrea N-M, Alexis FT, Benoit B, Diane PC, Ryan C, Theodore CB, Bruno M, Ashish B, Valéry L. Evidence-based recommendations on the use of intravenous lipid emulsion therapy in poisoning. Clin Toxicol (Philadelphia, Pa). 2016;54(10):899–923.
Kuo I, Akpa BS. Validity of the lipid sink as a mechanism for the reversal of local anesthetic systemic toxicity: a physiologically based pharmacokinetic model study. Anesthesiology. 2013;118(6):1350–61. https://doi.org/10.1097/ALN.0b013e31828ce74d[doi].
Clarkson CW, Hondeghem LM. Mechanism for bupivacaine depression of cardiac conduction: fast block of sodium channels during the action potential with slow recovery from block during diastole. Anesthesiology. 1985;62(4):396–405.
Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health. 1997;13(4):407–84. https://doi.org/10.1177/074823379701300401.
Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–76. https://doi.org/10.1002/jps.20322.
Coyle DE, Denson DD, Thompson GA, Myers JA, Arthur GR, Bridenbaugh PO. The Influence of lactic acid on the serum protein binding of bupivacainespecies differences. Anesthesiology. 1984;61(2):127–33.
Dennhardt R, Fricke M, Stöckert G. Metabolism and distribution of bupivacaine-experiments in rats. II. Distribution and elimination. Anaesthesist. 1978;27(10):86–92.
Thompson GA, Myers JA, Turner PA, Denson DD, Coyle DE, Ritschel WA. Influence of cimetidine on bupivacaine disposition in rat and monkey. Drug Metab Dispos. 1984;12(5):625–30.
Michael S, Robert B, Kevin BF, Banks HT. Validation of a mathematical model for green algae (Raphidocelis subcapitata) growth and implications for a coupled dynamical system with Daphnia magna. Appl Sci. 2016;6(5):155.
Banks HT, Collins E, Flores K, Pershad P, Stemkovski M, Stephenson L. Statistical error model comparison for logistic growth of green algae (Raphidocelis subcapitata). Appl Math Lett. 2017;64:213–22. https://doi.org/10.1016/j.aml.2016.09.006.
Everett RA, Zhao Y, Flores KB, Kuang Y. Data and implication based comparison of two chronic myeloid leukemia models. Math Biosci Eng. 2013;10(5–6):1501–18. https://doi.org/10.3934/mbe.2013.10.1501.
Banks HT, Flores KB, Hu S, Rosenberg E, Buzon M, Yu X, Lichterfeld M. Immuno-modulatory strategies for reduction of HIV reservoir cells. J Theor Biol. 2015;372:146–58. https://doi.org/10.1016/j.jtbi.2015.02.006.
Finkel DE. DIRECT Optimization Algorithm User Guide. Center for Research in Scientific Computation, North Carolina State University. 2003. https://repository.lib.ncsu.edu/handle/1840.4/484
Banks HT, Bekele-Maxwell K, Bociu L, Noorman M, Tillman K. The complex-step method for sensitivity analysis of non-smooth problems arising in biology. Center for Research in Scientific Computation, North Carolina State University. 2015. https://projects.ncsu.edu/crsc/reports/ftp/pdf/crsc-tr15-11.pdf
Banks HT, Hu S, Thompson WC. Modeling and Inverse Problems in the Presence of Uncertainty. 1st ed. New York: Chapman & Hall/CRC, 2014.
Baraldi R, Cross K, McChesney C, Poag L, Thorpe E, Flores KB, Banks HT. Uncertainty quantification for a model of HIV-1 patient response to antiretroviral therapy interruptions. Am Control Conf (Acc). 2014;2014:2753–8.
Banks HT, Baraldi R, Cross K, Flores K, Mcchesney C, Poag L, Thorpe E. Uncertainty quantification in modeling HIV viral mechanics. Math Biosci Eng. 2015;12(5):937–64. https://doi.org/10.3934/mbe.2015.12.937.
Adoteye K, Banks HT, Flores KB, LeBlanc GA. Estimation of time-varying mortality rates using continuous models for Daphnia magna. Appl Math Lett. 2015;44:12–6. https://doi.org/10.1016/j.aml.2014.12.014.
Banks HT, Tran HT. Mathematical and Experimental Modeling of Physical and Biological Processes. 1st ed. New York: Chapman & Hall/CRC, 2009.
Banks HT, Flores KB, Langlois CR, Serio TR, Sindi SS. Estimating the rate of prion aggregate amplification in yeast with a generation and structured population model. Inverse Probl Sci Eng. 2018;26(2):257–79. https://doi.org/10.1080/17415977.2017.1316498.
Mauch J, Martin Jurado O, Spielmann N, Bettschart-Wolfensberger R, Weiss M. Comparison of epinephrine vs lipid rescue to treat severe local anesthetic toxicity—an experimental study in piglets. Pediatr Anesth. 2011;21(11):1103–8. https://doi.org/10.1111/j.1460-9592.2011.03652.x.
McLachlan GJ, Lee SX, Rathnayake SI. Finite mixture models. Ann Rev Stat Appl. 2019;6(1):355–78. https://doi.org/10.1146/annurev-statistics-031017-100325.
Baudry J, Raftery AE, Celeux G, Lo K, Gottardo R. Combining mixture components for clustering. J Comput Graph Stat. 2010;19(2):332–53. https://doi.org/10.1198/jcgs.2010.08111.
Pearl J. Causality: models, reasoning and inference. 2nd ed. Cambridge: Cambridge University Press; 2009.
Pearl J. An introduction to causal inference. Int J Biostat. 2010. https://doi.org/10.2202/1557-4679.1203.
Textor J, Hardt J, Knüppel S. DAGitty: a graphical tool for analyzing causal diagrams. Epidemiology. 2011;22(5):745. https://doi.org/10.1097/EDE.0b013e318225c2be.
Weinberg G, Lin B, Zheng S, Di Gregorio G, Hiller D, Ripper R, Edelman L, Kelly K, Feinstein D. Partitioning effect in lipid resuscitation: further evidence for the lipid sink. Crit Care Med. 2010;38(11):2268–9. https://doi.org/10.1097/CCM.0b013e3181f17d85.
Denson D, Coyle D, Thompson G, Myers J. Alpha 1-acid glycoprotein and albumin in human serum bupivacaine binding. Clin Pharmacol Ther. 1984;35(3):409–15. https://doi.org/10.1038/clpt.1984.51.
Tucker GT, Boyes RN, Bridenbaugh PO, Moore DC. Binding of anilide-type local anesthetics in human plasma. I. Relationships between binding, physicochemical properties, and anesthetic activity. Anesthesiology. 1970;33(3):287–303. https://doi.org/10.1097/00000542-197009000-00002.
Fettiplace MR, Akpa BS, Rubinstein I, Weinberg G. Confusion about infusion: rational volume limits for intravenous lipid emulsion during treatment of oral overdoses. Ann Emerg Med. 2015;66(2):185–8. https://doi.org/10.1016/j.annemergmed.2015.01.020.
Acknowledgements
The authors would like to thank Dr Guy Weinberg for sharing the physiological data from his prior publication [1] for use in this study. This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
Research sponsored by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U. S. Department of Energy. BS Akpa and KB Flores also acknowledge institutional start-up funds provided by North Carolina State University.
Conflict of interest
Matthew McDaniel and Kevin Flores declare that they have no conflict of interest. Belinda Akpa has previously consulted for ResQ Pharma, Inc., a biopharmaceutical company focused on lipid rescue therapy.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Availability of data and material
Study data were pre-existing. The code used to generate simulation data is available from the corresponding author on reasonable request.
Authors’ contributions
Conceptualization: Belinda S. Akpa (equal), Kevin B. Flores (equal). Methodology: Kevin B. Flores (equal), Matthew McDaniel (equal), Belinda S. Akpa (equal). Formal analysis and investigation: Belinda S. Akpa (lead), Matthew McDaniel (supporting). Writing—original draft: Matthew McDaniel (equal), Belinda S. Akpa (equal). Writing—review and editing: Belinda S. Akpa (lead), Kevin B. Flores (supporting).
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
McDaniel, M., Flores, K.B. & Akpa, B.S. Predicting Inter-individual Variability During Lipid Resuscitation of Bupivacaine Cardiotoxicity in Rats: A Virtual Population Modeling Study. Drugs R D 21, 305–320 (2021). https://doi.org/10.1007/s40268-021-00353-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40268-021-00353-4