FormalPara Key Points

Introduction of a novel method for detecting safety signals for MedDRA-coded adverse events (AEs) in a randomized controlled trial.

BAHAMA can use the complete MedDRA structure to borrow strength between closely related AEs.

1 Introduction

Randomized controlled trials (RCTs) are primarily designed and conducted to provide reliable estimates of the efficacy of an intervention. During an RCT, adverse events (AEs) are often collected along with the primary outcome. An AE is defined as “any untoward medical occurrence that may occur during treatment with a pharmaceutical product but does not necessarily have a causal relationship with this treatment” [1]. It is important to identify/detect AEs with a higher incidence in the treatment group compared with the control population. In addition, AEs with a lower incidence in the treatment group compared with the control population are also important.

To structure the AEs, the Medical Dictionary for Regulatory Activities® (MedDRA) has been developed. MedDRA is a hierarchical standardization terminology reporting AEs in four levels [2]. The lowest level, Preferred Terms (PTs), is a single type of medical event. PTs are aggregated into higher levels (i.e. Higher Level Terms [HLT], Higher Level Group Terms [HLGT] and System Organ Classes [SOC]). MedDRA has a multiaxial structure where a single lower level could be aggregated in multiple higher levels. The levels provide a grouping of the AEs based on anatomical, pathological, physiological, etiological, or functional similarities [3]. It is therefore reasonable to assume that AEs closely related to each other by this MedDRA structure are affected similarly by a treatment or decease [4].

The analysis of AEs is less straightforward than the single primary outcome. In general, the power calculations to determine the sample size of RCTs are not focused on AEs, and AEs are observed with low incidence rates. As a result, there is usually limited statistical power to detect rare AEs, leading to a high rate of false negatives. Moreover, testing many different AEs independently leads to a multiple testing problem. Corrections for the multiple testing such as the Bonferroni correction increases the false-negative rate, but this approach can be overly conservative [5].

To deal with the multiple testing problem, Mehrotra and Heyse [6] developed the double false discovery rate (Double FDR) approach. This approach uses two-step adjusted p-values based on the Benjamini and Hochberg FDR. A simplified explanation of the Double FDR approach is first to adjust the p-values of the SOCs and then to adjust the p-values within a SOC.

As an RCT is often not powered to detect AEs, we hypothesize that a Bayesian approach is useful. A Bayesian approach testing the null hypothesis of no difference between the treatment groups is based on the posterior probability of the incidence rate being higher than one [4]. Several authors have proposed Bayesian methods but currently use only two MedDRA levels, the PT level and the primary SOC level, and a third prior level. The other MedDRA levels (mainly HLT and HLGT) are only used for data visualization, even though they may provide a clinically relevant grouping of PTs [1, 4, 7,8,9]. Berry and Berry [10] proposed a three-stage Bayesian hierarchical model for analyzing AE data in clinical trials. They treat AE data as binary since most AEs occur so infrequently that a dichotomization per patient is reasonable. Next, they model AEs with a hierarchical structure under the condition that AEs under the same SOC are more similar and medically related than those under distinct SOCs. Xia et al. [11] extended the Bayesian hierarchical model to a Poisson model to account for differences in treatment duration between treatment groups [9].

A drawback of using only the PT and SOC levels in the hierarchical model is that with an increasing number of PTs, the performance of these three-stage Bayesian hierarchical models deteriorates [11, 12]. The SOC covers many PTs, and these PTs are not necessarily strongly medically related. Another drawback of the model proposed by Berry and Berry [10] is that recurring AEs within the same patient are excluded. To account for the recurring AEs, we propose using a Poisson distribution to model the AEs, using the total number of patients within a treatment group as an offset in the Poisson model. Furthermore, we propose using data aggregation for uncommon AEs at a higher level within the MedDRA structure. By using aggregated AE counts, even AEs with a very low incidence are taken into account. Furthermore, we propose to include the complete hierarchy.

In summary, we propose extending the hierarchy used by others to group the AEs to the complete hierarchy of the MedDRA. We developed our multi-stage hierarchical model, including the complete multiaxial MedDRA structure and developed a Bayesian algorithm to estimate posterior probabilities. We illustrated our model with AE data from a large RCT, and we compared results with other methods for analyzing AEs.

2 Method

The MedDRA structure has four levels; the PT level, HLT level, HLGT level and the SOC level. Now, consider that we have count data from \(N_{4}\) AEs at the PT level (4th MedDRA level). The numbers of AEs in the control group are given by \(Y^{{\left( {0,4} \right)}} = \left( {y_{1}^{{\left( {0,4} \right)}} \ldots y_{i}^{{\left( {0,4} \right)}} \ldots .y_{{N_{4} }}^{{\left( {0,4} \right)}} } \right)\) and AEs in the treatment group by \(Y^{{\left( {1,4} \right)}} = \left( {y_{1}^{{\left( {1,4} \right)}} \ldots y_{i}^{{\left( {1,4} \right)}} \ldots . y_{{N_{4} }}^{{\left( {1,4} \right)}} } \right)\). We assume that the PT-level AE count \(y_{i}^{{\left( {x,4} \right)}}\), where \(x \in 0,1\) and \(i = 1 \ldots N_{4}\), follows a Poisson distribution, that is,

$$y_{i}^{{\left( {x,4} \right)}} \sim {\text{Poisson}}\left( {\lambda_{i}^{{\left( {x,4} \right)}} } \right),$$

where the intensity parameter \(\lambda_{i}^{{\left( {x,4} \right)}}\) is a function of a treatment-indicator variable \(x\) and, if necessary, possible other covariates. The log intensity is given by

$${\text{log}}\left( {\lambda_{i}^{{\left( {x,4} \right)}} } \right) = a_{i} + b_{i} \times x + {\text{log}}\left( {N^{x} } \right),$$

where the parameter \(a_{i}\) describes the log intensity of PT \(i\) in the control group and \(a_{i} + b_{i}\) similarly in the treatment group. Note that \(b_{i}\) is the log rate ratio (log RR). To adjust for an unequal number of subjects within each treatment group, an offset log(\(N^{x} )\) is used, where \(N^{x}\) is the number of subjects within each group.

The PT-level adverse events are clustered at the HLT level (3rd MedDRA level). To use this clustering of AEs, we define a random-effects model for parameters \(a_{i}\) and \(b_{i}\). We assume that the parameters from adverse event \(i\) follow a bivariate normal distribution with mean and covariance matrix depending on the HLT level, that is,

$$\left( {a_{i} , b_{i} } \right)\sim N\left( {\mathop \sum \limits_{j = 1}^{{N_{3} }} W_{ij}^{\left( 3 \right)} \mu_{j}^{\left( 3 \right)} , \mathop \sum \limits_{j = 1}^{{N_{3} }} W_{ij}^{\left( 3 \right)} {\Sigma }_{j}^{\left( 3 \right)} } \right),$$

where \(W_{ij}^{\left( 3 \right)}\) is a (fixed) weight indicating membership of PT \(i\) in HLT \(j\) \(\left( {j = 1 \ldots N_{3} } \right)\). In addition, \(\mu_{j}^{\left( 3 \right)}\) are the average log intensity of the control group and log RR of the PTs in the same HLT category and \({\Sigma }_{j}^{\left( 3 \right)}\) is the dispersion of PTs in the same HLT category.

For the higher MedDRA levels (HLGT and SOC MedDRA levels), we repeat the same procedure:

$$\mu_{j}^{\left( 3 \right)} \sim N\left( {\mathop \sum \limits_{k = 1}^{{N_{2} }} W_{jk}^{\left( 2 \right)} \mu_{k}^{\left( 2 \right)} , \mathop \sum \limits_{k = 1}^{{N_{2} }} W_{jk}^{\left( 2 \right)} {\Sigma }_{k}^{\left( 2 \right)} } \right),$$

where \(W_{jk}^{\left( 2 \right)}\) is a (fixed) weight indicating membership of HLT \(j\) in HLGT \(k\) (\(k = 1 \ldots N_{2} )\). The parameters \(\mu_{k}^{\left( 2 \right)}\) and \({\Sigma }_{k}^{\left( 2 \right)}\) are the averages and dispersion of HLTs in the same HLGT category and are given by

$$\mu_{k}^{\left( 2 \right)} \sim N\left( {\mathop \sum \limits_{l = 1}^{{N_{1} }} W_{kl}^{\left( 1 \right)} \mu_{l}^{\left( 1 \right)} , \mathop \sum \limits_{l = 1}^{{N_{1} }} W_{kl}^{\left( 1 \right)} {\Sigma }_{l}^{\left( 1 \right)} } \right),$$

where \(W_{kl}^{\left( 1 \right)}\) is a (fixed) weight indicating membership of HLGT \(k\) in SOC \(l\) (\({\text{l}} = 1 \ldots N_{1} )\). In addition, \(\mu_{l}^{\left( 1 \right)}\) and \({\Sigma }_{l}^{\left( 1 \right)}\) are the averages and dispersion of HLGTs in the same SOC category.

For the SOC-level log intensity of the control group and log RR we assume a bivariate normal distribution \(\mu_{l}^{\left( 1 \right)} \sim N\left( {\mu^{\left( 0 \right)} ,{\Sigma }^{\left( 0 \right)} } \right)\). We assume \({\Sigma }_{j}^{\left( 3 \right)} , {\Sigma }_{k}^{\left( 2 \right)}\) and \({\Sigma }_{l}^{\left( 1 \right)}\) to be diagonal, and therefore do not model the correlation between log intensity parameters and all elements to have weakly informative exponential prior distribution \(\left( {{\text{Exp}}\left( 1 \right)} \right)\).

We use a Bayesian estimation framework and therefore specified prior distributions of the \(\mu^{\left( 0 \right)}\) \(( N\left( {0,1} \right)\)) and again, we assume \({\Sigma }^{\left( 0 \right)}\) to be diagonal and all elements to have an exponential prior distribution \(\left( {{\text{Exp}}\left( 1 \right)} \right)\).

3 Extensions for More Complex Data

We extend the model to include the multiaxiality of the MedDRA structure, and to deal with the low incidence of some PTs, we introduce data aggregation.

3.1 Multiaxiality of the MedDRA Structure

In section 2 we defined the hierarchical MedDRA structure with the three matrices \(W_{{}}^{\left( 3 \right)} , W_{{}}^{\left( 2 \right)}\), and \(W_{{}}^{\left( 1 \right)}\). When no multiaxiality is present, all PTs, HLTs, and HLGTs can only belong to a single HLT, HLGT, or SOC, respectively. In this case, the three corresponding weight matrices consist of binary indicators. The sum of all rows of these matrices must be one.

To deal with multiaxiality, we propose to modify the matrices \(W_{{}}^{\left( 3 \right)} , W_{{}}^{\left( 2 \right)}\), and \(W_{{}}^{\left( 1 \right)}\) such that PTs, HLTs, and HLGTs can belong to multiple parents. Instead of binary indicators, we allow all matrices to contain weights between zero and one. The sums of memberships of all PTs, HLTs, and HLGTs must still sum up to one. A simple example of a weight matrix is:

$$\begin{array}{*{20}c} {} & {{\text{HLT}}\;1} & {{\text{HLT}}\;2} & {{\text{HLT}}\;3} & {{\text{HLT}}\;4} \\ {{\text{PT}}\;1} & 1 & 0 & 0 & 0 \\ {{\text{PT}}\;2} & 1 & 0 & 0 & 0 \\ {{\text{PT}}\;3} & 0 & 1 & 0 & 0 \\ {{\text{PT}}\;4} & 0 & 0 & 1 & 0 \\ {PT\;5} & 0 & 0 & {0.5} & {0.5} \\ {{\text{PT }}\;6} & 0 & 0 & 0 & 1 \\ \end{array}$$

In this example, PT 5 belongs to HLT 3 and HLT 4. A natural choice of weights is to assign half of the weight to HLT 3 and the other half to HLT 4. If necessary, however, it is possible to change the weight such that the primary parent has more weight compared with the secondary parent. Within the current implementation of BAHAMA in an R-package, weights can be specified by the user, as long as the sum of the weights of a single PT, HLT, or HLGT is 1.

3.2 Data Aggregation

In cases where the incidence of a PT is very low, estimating the log RR might not be possible without the use of strong prior knowledge. To increase the accuracy of the estimated log RR we propose to aggregate these very low incidence PTs to their corresponding HLTs. We set a threshold on the incidence of PTs within our proposed model of 5, meaning if the PT is recorded 5 times or less in the RCT, combined in the control and treatment group, the PTs are aggregated into the HLT. Let \(y_{{}}^{{\left( {x,3} \right)}}\) be vectors of the HLT counts of the treatment and control group of these aggregated PTs.

Apart from the low incidence of PTs, the number of siblings is also an essential restriction in our model. A single PT does not allow borrowing of information from other PTs, as there is no other PT to borrow information from. If a PT does not have any siblings, or is below a threshold, the counts will also be aggregated to their corresponding HLT.

Even on the HLT level, the incidence can be below the threshold, or a HLT can have too few siblings, so aggregating to the HLGT level might also be needed. The counts of the HLT level are summarized in their HLGT level, in \(y_{{}}^{{\left( {x,2} \right)}}\) for the treatment and control group.

An illustration of the filtering process can be seen in Fig. 1. In this example, PT 5 and PT 6 are low-incidence PTs. They are first aggregated into HLT 4. However, even HLT 4 is below the threshold and is aggregated into HLGT 2. PT 3 does not have any siblings, and therefore is aggregated into HLT 2. PT 4 did have a sibling, PT 5, but PT 5 was removed based on low incidence, so PT 4 is also aggregated in HLT 3. HLT 3 also includes the counts of PT 5.

Fig. 1
figure 1

Illustration of the data aggregation based on two selections; red: incidence, green: structure

Full size image

For the HLTs that are not modeled at the PT level, we again assume a Poisson distribution to model the counts. To make the scale comparable across the stages, the average incidence is adjusted by multiplying by the number of PTs of the HLT \(j\).

$$y_{j}^{{\left( {x,3} \right)}} \sim {\text{Poisson}}\left( {\lambda_{j}^{{\left( {x,3} \right)}} \times N_{j}^{{{\text{PT}}}} } \right)$$
$$\log \left( {\lambda_{j}^{\left( 3 \right)} } \right) = \mu_{j}^{{\left( {0,3} \right)}} + \mu_{j}^{{\left( {1,3} \right)}} \times x + \log \left( {N^{x} } \right)$$

For the HLGTs that are not included in the PT or HLT level:

$$y_{j}^{{\left( {x,2} \right)}} \sim {\text{Poisson}}\left( {\lambda_{k}^{{\left( {x,2} \right)}} \times N_{k}^{{{\text{PT}}}} } \right)$$
$$\log \left( {\lambda_{k}^{\left( 2 \right)} } \right) = \mu_{k}^{{\left( {0,2} \right)}} + \mu_{k}^{{\left( {1,2} \right)}} \times x + \log \left( {N^{x} } \right)$$

4 Data Analysis

4.1 Simulation Study

We simulated AE data for p = \(1 \ldots N^{{{\text{pat}}}}\) patients and \(N\) PTs. We started by simulating a vector \(x\) of length \(N^{{{\text{pat}}}}\), assigning every patient to the simulated control (\(x = 0\)) or treatment (\(x = 1\)) group. A MedDRA structure was randomly sampled from the real MedDRA structure of the RCT of the case study. PTs were drawn from a Poisson distribution with parameters drawn from the distributions of HLT, HLGT and SOC levels according to the hierarchical Bayesian model.

$$\begin{gathered} x\left[ p \right]\sim {\text{Bernoulli}}\left( {0.5} \right) \hfill \\ \mu_{k}^{{\left( {0,2} \right)}} \sim N\left( {\mu_{l}^{{\left( {0,1} \right)}} ,\sigma^{2} } \right) \hfill \\ \end{gathered}$$
$$\begin{gathered} \mu_{k}^{{\left( {1,2} \right)}} \sim N\left( {{\text{log}}\left( {RR} \right),\sigma^{2} } \right) \hfill \\ \mu_{j}^{{\left( {x,3} \right)}} \sim N\left( {\mu_{k}^{{\left( {x,2} \right)}} ,\sigma^{2} } \right) \hfill \\ \end{gathered}$$
$$\begin{gathered} a_{i} \sim N\left( {\mu_{j}^{{\left( {0,3} \right)}} ,\sigma^{2} } \right) \hfill \\ b_{i} \sim N\left( {\mu_{j}^{{\left( {1,3} \right)}} ,\sigma^{2} } \right) \hfill \\ \end{gathered}$$
$$\begin{gathered} a_{i} \sim N\left( {\mu_{j}^{{\left( {0,3} \right)}} ,\sigma^{2} } \right) \hfill \\ {\text{log}}\left( {\uptau } \right)\left[ p \right] = a\_i + b\_i \times x\left[ p \right]) \hfill \\ y\left[ {p,i} \right]\sim {\text{Poisson}}\left( {{\uptau }\left[ {p,i} \right]} \right) \hfill \\ \end{gathered}$$

We simulated 72 scenarios varying the number of patients (\(N^{{{\text{pat}}}} \; = \;1000, \;2000\)), the number of PTs (\(N\; = \;1000,\; 2000,\; 4000\)), the average incidence PT within a SOC (\({\text{exp}}\left( {{\upmu }_{l}^{{\left( {0,1} \right)}} } \right)\; = \;0.01,1,5\)), and the effect of a treatment by varying the log RR (log(RR) = 0.01, 1, 0.5, 0.1) and all small variances (\(\sigma^{2}\) = 0.1). For each scenario we simulated 500 datasets.

For all scenarios, we used the default thresholds for incidence of 5 and number of siblings of 2. For the scenario of an average incidence of 0.01 and log RR of 1, we varied the thresholds for incidence between 1 and 10 and for the number of siblings between 2 or 5.

Performance of our model was quantified with (1) the mean squared error (MSE) between the true log RR and the posterior mean log RR by the various methods, (2) the bias between the true log RR and the posterior mean log RR, (3 the coverage of the 95% credibility intervals (CI) defined as the number of times the true log RR was within the 95% CI of the posterior log RR. Simulations with non-converging posterior samples were excluded from calculation of the performance measures.

4.2 Case Study

For our case study we compared results of our five-stage hierarchical Bayesian model with the existing implementation of the Double FDR approach proposed by Mehrotra and Heyse [6] and an implementation of the three-stage hierarchical Bayesian model by Berry and Berry [10]. For the model by Berry and Berry [10], PT counts were dichotomized as zero or ≥ 1.

4.3 Bayesian Computation

We implemented our model in the Stan probabilistic programming language, which estimates the posterior distributions for the parameters of interest by using Hamiltonian Markov Chain Monte Carlo (HMC) [13]. Stan was used with the default settings: four chains with 1000 warm-up iterations, 1000 samples of the posterior distributions per chain to calculate summarizing statistics. No alterations on the default values of the maximum allowed tree-depth or adapt delta parameters were needed for our analyses as they all reached convergence with these settings. Convergence was assessed by visual inspection of traceplots as well as the \(\widehat{R}\) convergence diagnostic (1.1 in case study, 1.4 in simulation study).

We implemented the three-stage hierarchical Bayesian model by Berry and Berry [10] in the programming language JAGS [14], with four chains, 10,000 sample warm-up iterations, 10,000 samples of the posterior distributions per chain, with a thinning of 10, to calculate summarizing statistics.

5 Results

Figure 2 gives a summary of the results of the simulation study of the PT level. Overall, the average bias between the true log RRs and the posterior mean of the log RRs of our model was around 0. The MSE between the true log RRs and the posterior mean log RRs of our model decreased with an increasing average incidence of PTs. There was no difference in the outcome performance with an increasing RR; the results per true log RR are in the electronic supplementary material (ESM). The coverage of the 95% credibility intervals on the PT level was on average 94%, and this did not vary with an increasing average incidence.

Fig. 2
figure 2

Bias and the mean square error (MSE) between the true log rate ratio (RR) and the posterior mean log RR for different scenarios of the simulation study. AE adverse events, PTs Preferred Terms

Full size image

We introduced a data aggregation process as a preprocessing step with this method. Within this data aggregation process, two thresholds were set. The first threshold is on the minimal incidence and the second on the number of siblings within the MedDRA structure. This preprocessing step is needed because the model runs into convergence issues with the default settings of the HMC. To illustrate these issues, Fig. 3 gives the convergency statistic \(\widehat{R}\), a measure for how well the chains have mixed per parameter, for the posterior mean log RRs of our model for multiple threshold settings of the data aggregation process. The number of parameters without fully mixed chains increased with lower thresholds on the number of siblings and the incidence. There were fewer not fully mixed chains with higher thresholds on the number of siblings.

Fig. 3
figure 3

An indication of the convergence issues with varying thresholds on the Preferred Term (PT) level (Rhat < 1.1 indicates fully mixed chains)

Full size image

As for the performance measures with a varying threshold, Fig. 4 shows the performance measures given different threshold settings. The bias of the posterior mean log RRs was close to zero for all thresholds. The MSE of the posterior mean log RRs decreased with increasing thresholds on the PT level. For the HLT level, the MSE was less affected by the threshold settings in the aggregation process.

Fig. 4
figure 4

The bias and mean square error (MSE) for the posterior mean log rate ratios (RRs) for the same simulation dataset for different thresholds (PT-level and HLT-level). HLT Higher Level Terms, PT Preferred Terms

Full size image

5.1 Case Study

An RCT was conducted to examine the use of statins in patients undergoing hemodialysis. Details of the RCT can be found in the original manuscript by Fellström et al. [15]. In short, 2776 patients were followed for an average of 3.2 years. Half of these patients were treated with a statin and half received a placebo. In total, 36,821 different AEs were recorded in 2658 patients, grouped into 2195 PTs, 724 HLTs, 244 HLGTs and 24 SOCs. The most common AE being diarrhea, reported 1000 times by 616 patients.

After applying the two thresholds on the data, a total of 574 PTs (\({y}^{\left(x,4\right)}\)), 167 HLTs (\({y}^{\left(x,3\right)}\)), 127 HLGTs (\({y}^{\left(x,2\right)}\)) remained. Of the 574 PTs, 9 had multiple HLTs, 8 out of the 327 HLTs were clustered into multiple HLGTs, and 5 out of the 244 HLGTs clustered into multiple SOCs. Convergence was reached using the default settings in Stan; the highest \(\widehat{R}\) was 1.099.

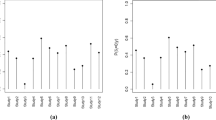
In Fig. 5, the posterior mean log RRs are shown for the four MedDRA levels. A table with the posterior mean and standard deviation (SD) of the log RRs is in the ESM. On the PT level, the most notable PTs were ‘discomfort’ and ‘pulmonary oedema’. Both of these PT incidences were increased in the treatment group. On the HLT level; the HLTs of 'muscle weakness conditions' and 'heart failure signs' were both increased in the treatment group.

Fig. 5
figure 5

The posterior probability of an effect between the statin treatment group and placebo group and its magnitude as the posterior mean of the log rate ratio (RR) divided by the posterior standard deviation per MedDRA levels. HLGT Higher Level Group Terms, HLT Higher Level Terms, PT Preferred Terms, SD standard deviation, SOC System Organ Classes

Full size image

5.2 Comparison

To illustrate the effect of shrinkage we compared the posterior mean log RRs of the PTs of our model with the observed log RRs and log odds ratios in Fig. 6A, B. Some posterior mean log RRs were closer to zero than the observed log RRs, thereby decreasing the false discovery rate, whereas other posterior mean log RRs were drawn away from zero, due to borrowing strength from closely related PTs.

Fig. 6
figure 6

Comparison between A observed log RR and B log OR of the PTs, C, D the posterior mean log ORs as estimated by the model of Berry and Berry [10], E the DFDR and the posterior mean log RRs (1, Pulmonary oedema; 2, Basal Cell Carcinoma; 3, Discomfort). DFDR double false discovery rate, OR odds ratio, PTs Preferred Terms, RR rate ratio, SD standard deviation, SOC System Organ Classes

Full size image

To support the findings of our five-stage hierarchical model, we compared the results on the PT level with other methods developed for AE analyses. We compared our posterior mean log RRs with the posterior mean log odds ratios (OR) given by the model as proposed by Berry and Berry [10] (Fig. 6). The PT with the highest log OR is ‘Basal cell carcinoma’; this finding was also supported by the five-stage model. The log OR of the PT ‘discomfort’, the PT with the highest log RR, was close to zero. The occurrence of this PT is high, especially in the treatment group, but occurred in relatively few patients (29 times in 6 patients in the treatment group versus 3 times in 3 patients in the control group); this aspect is lost when PTs are dichotomized as is done with Berry and Berry’s model.

The PT ‘pulmonary oedema’ is an example of the benefit of using all MedDRA levels (91 times in 61 patients in the treatment group vs 43 times in 41 patients in the control group). This PT is part of HLT ‘pulmonary oedemas’ together with the PTs ‘Acute pulmonary oedema’ (39 in 31 and 24 in 20) and ‘Pulmonary congestion’ (9 in 8 and 12 in 11). Both the PTs ‘pulmonary oedema’ and ‘acute pulmonary oedema’ were more common in the treatment group, but based on the observed individual incidences were not signaled out. With the shrinkage that was enforced by a Bayesian model only based on the SOC level, the PTs were also not signaled out.

Another method especially developed for AE data is the double FDR procedure. We compared double FDR p-values at the PT level with p-values from the five-stage model, if possible (Fig. 6E). The double FDR procedure was performed for 538 of the 574 PTs, and those 538 PTs were from 21 SOCs. All PTs with a significant p-value of < 0.05 according to the double FDR procedure were also found by the five-stage model. The five-stage model signaled 12 additional PTs, in comparison with the double FDR.

6 Discussion

This paper introduces a novel approach using a Bayesian hierarchical model for analyzing MedDRA-coded AEs collected during an RCT. The use of a Bayesian hierarchical model has some advantages. The first is that by using the existing MedDRA structure to borrow strength between closely related AEs, more stable estimations of incidence parameters are obtained. In comparison with other methods, we use the complete MedDRA structure, making it more likely that the effect of treatment is comparable between the AEs. Second, we propose aggregating the data to a higher MedDRA level if not enough data is available. By aggregating the PTs into higher levels, all available data is still included in the model, even when the incidence of a specific PT is too low to estimate the difference between the treatment and control group. The 'borrowing' of information on the higher levels is more complete by using this form of aggregating than by not including this data in the data analysis.

A limitation of methods like the one we propose here is that they are not used in practice, as there is little to no guidance in using the methods nor is there user-friendly software [1, 7]. Therefore, we made this model and the data aggregation into the R package Bayesian Hierarchical Analyses of MedDRA-coded Adverse Events (BAHAMA). This R package and a tutorial is available on https://github.com/Alma-Revers/BAHAMA.

A hierarchical Bayesian approach applies shrinkage to the effect of treatment on the incidence of the AEs. The direction and the amount of shrinkage is determined by the weight matrices and is based on the MedDRA structure. This shrinkage is sub-optimal when the interest is in specific outlying AEs, as the shrinkage smooths the effect of the outlier, making it less likely to be detected. We argue that this shrinkage is mostly beneficial as it increases the probability of detecting a true effect overall. However, the proposed model might not be the optimal choice if a specified AE is of particular interest.

With our multi-level hierarchical Bayesian model, convergence issues may occur. In our case study we did not encounter any convergence issues with the thresholds that we used for the incidence and the number of MedDRA siblings. Our simulation study had some convergence issues that could be avoided by increasing these thresholds and by drawing more samples from the posterior distributions. Other solutions are changing the settings of the HMC sampling or use an alternative parameterization of the model such as models in which the intensity of the treatment group is independent of the intensity of the control group.

With a full Bayesian framework, the conclusion might change based on the priors. We choose to use weakly informative priors instead of relying on medical knowledge. In order to evaluate the effect of the prior specifications, we carried out a sensitivity analysis in which we used more informative and less informative priors. In summary, with less informative priors, we had more convergence issues. However, the difference in results was small. Therefore, we concluded that with the proposed priors, results are robust.

In the models by Berry and Berry (2004) and Xia et al. (2011), a zero-point mass was added to the log OR [10, 16]. The intuition behind this is that there will be no difference between the treatment groups for most AE/PTs. We did this for our model as well. However, this did perform worse in terms of convergence with our case data. Therefore, we did not pursue this approach any further.

7 Conclusion

This paper introduces a new approach to analyzing AE data from an RCT, by using the MedDRA structure and by borrowing strength from closely related AEs and data aggregation. With our case study we showed that this new approach could detect more AEs compared with other approaches. We implemented the new method in the R package BAHAMA. We have currently only implemented this method for RCTs comparing two interventions. In the future this will be extended for multi-arm RCTs.