A Method to Combine Signals from Spontaneous Reporting Systems and Observational Healthcare Data to Detect Adverse Drug Reactions

Abstract

Introduction

Observational healthcare data contain information useful for hastening detection of adverse drug reactions (ADRs) that may be missed by using data in spontaneous reporting systems (SRSs) alone. There are only several papers describing methods that integrate evidence from healthcare databases and SRSs. We propose a methodology that combines ADR signals from these two sources.

Objectives

The aim of this study was to investigate whether the proposed method would result in more accurate ADR detection than methods using SRSs or healthcare data alone.

Research Design

We applied the method to four clinically serious ADRs, and evaluated it using three experiments that involve combining an SRS with a single facility small-scale electronic health record (EHR), a larger scale network-based EHR, and a much larger scale healthcare claims database. The evaluation used a reference standard comprising 165 positive and 234 negative drug–ADR pairs.

Measures

Area under the receiver operator characteristics curve (AUC) was computed to measure performance.

Results

There was no improvement in the AUC when the SRS and small-scale HER were combined. The AUC of the combined SRS and large-scale EHR was 0.82 whereas it was 0.76 for each of the individual systems. Similarly, the AUC of the combined SRS and claims system was 0.82 whereas it was 0.76 and 0.78, respectively, for the individual systems.

Conclusions

The proposed method resulted in a significant improvement in the accuracy of ADR detection when the resources used for combining had sufficient amounts of data, demonstrating that the method could integrate evidence from multiple sources and serve as a tool in actual pharmacovigilance practice.

Introduction

Adverse drug reactions (ADRs) are known to cause high morbidity and mortality and cost several billion dollars annually [1–3]. In addition to the ADRs detected during pre-marketing clinical trials, unanticipated ADRs may occur after a drug has been approved, attributable to its use, which may be prolonged, on large, diverse populations [4]. Therefore, the post-marketing surveillance of drugs is essential for generating more complete drug safety profiles and for providing a decision-making tool to help governmental drug administration agencies take an action on the marketed drugs [5, 6].

Analysis of spontaneous reports of suspected ADRs has traditionally served as a valuable tool in the detection of previously unknown ADRs in post-marketing surveillance [7, 8]. Spontaneous reporting systems (SRSs) can be effective in revealing unusual or rare adverse events that occur with the initial use or short-term use of medications [9]. However, SRSs do not rapidly lead to ADR detection if the adverse event is relatively common but not necessarily drug-related in the general population, and SRSs are also known for limitations such as under-reporting and biased reporting influenced by media coverage or the length of time on the market [10–12]. Electronic healthcare data, such as electronic health records (EHRs) and administrative claims data, are starting to be used to complement SRSs [13–16]. Electronic healthcare data contain longitudinal patient information collected during routine clinical care, and have been used extensively in pharmacoepidemiology and pharmacoeconomics to study the natural history of disease and treatment utilization. Another opportunity for these data is to study the prevalence of a drug and an ADR, to explore the temporal relationship between exposure and outcome, and to reduce the reporting biases of SRSs. The appropriate use of healthcare data has the potential for earlier detection of drug safety signals before healthcare professionals report them to an SRS system [17]. With the ongoing development of the US Food and Drug Administration’s (FDA’s) Sentinel Initiative and similar systems around the world, near real-time active pharmacovigilance may soon be a reality [18]. Since the Sentinel system is based on administrative claims data captured as part of the reimbursement process surrounding routine clinical care, its value can be considered ‘complementary’ to the utility of SRSs. However, electronic healthcare data has its own limitations, which are different from the SRS limitations, since healthcare data usually mention the patient’s medications, symptoms, and diseases individually without mentioning explicit causal relationships, such as the indications for prescribing the medications.

Therefore, statistical methods, together with the use of temporality, are needed to infer an estimate of the strength of associations, without the benefit of an explicit reported ADR relationship. For example, a statistical association between a medication and a condition may be a treatment if the condition precedes the medication event, an ADR only if the condition follows the medication event, or an indirect association stemming from another event (e.g., a confounder). Considerable systematic studies of the potential value of these databases in post-marketing pharmacovigilance have been undertaken by the Observational Medical Outcomes Partnership (OMOP, http://omop.org) [16, 19, 20] and the European Union project Exploring and Understanding Adverse Drug Reactions (EU-ADR, http://euadr-project.org) [21].

Currently, research efforts are starting to focus on the use of multiple data sources, such as SRSs, electronic healthcare data, biomedical literature, and chemical information, to detect and validate novel ADRs. For example, Tatonetti et al. discovered a potentially new drug interaction, which can lead to unexpected increases in blood glucose levels, between paroxetine and pravastatin based on SRSs, and then validated this interaction using multi-center EHRs [22]. Duke et al. predicted probable novel myopathy-associated drug interactions based on the literature, and evaluated them using a large EHR database [23]. Vilar et al. re-ranked the ADR signals mined from a large-scale claims database using 2D structure similarity [24]. However, the above studies have used a single data resource to generate ADR signals and then have independently used another resource for validation or enrichment analysis. Harpaz et al. recently proposed a Bayes model to computationally combine a disparate SRS and a healthcare claims database, and the performance was shown to have promising results based on a reference standard provided by OMOP [25].

In addition to the large-scale claims and EHR databases used by the OMOP and EU-ADR projects, individual EHRs were shown to have potential for diverse types of studies, including pharmacovigilance, drug re-purposing and phenome-wide association scans (PheWAS) [26–28]. Our group conducted several studies based on the EHR from New York Presbyterian Hospital at Columbia University Medical Center (NYP/CUMC), and demonstrated its potential for drug safety studies. Additionally, we demonstrated that when using the EHR, confounding is one of the most important challenges that needs to be handled [14, 29–31]. Confounding is also an important issue when using the SRS databases. The main algorithm for detecting ADRs in SRSs is an approach referred to as disproportionality analysis, which compares the number of observed cases with that of expected cases [7]. Detecting ADRs in SRSs is challenging partly due to under-reporting of unexpected events, the lack of a priori knowledge and a bias towards well publicized ADRs [32]. Thus, there is an inherent tradeoff when detecting new ADRs by taking advantage of primary suspected information based on experts’ intuition which may be biased, possibly leading to delayed ADR detection, or detecting ADRs by considering concomitant medications as co-occurrence information, possibly leading to false positive signals. Several previous studies showed that multivariate logistic regression is helpful to guard against false positive signals due to confounding by concomitant drugs [33, 34].

Although both SRS and healthcare data represent unique challenges in their use, we believe that they complement each other along several dimensions that may improve pharmacovigilance [17, 25]. A challenge accompanied by the richness of information for pharmacovigilance practice occurs when these two resources provide conflicting or inconsistent information. Therefore, we propose a methodological framework to integrate analyses generated from the FDA Adverse Event Reporting System (FAERS) and from healthcare data. As part of the methodological framework, we incorporated a method to deal with confounding effects in NYP/CUMC EHR and the FAERS. We applied the method to four clinically serious ADRs: acute renal failure (ARF), acute liver injury (ALI), acute myocardial infarction (AMI), and upper gastrointestinal bleeding (GIB) [35] with an aim of demonstrating that signal discrimination performance can be improved by such an integrative strategy. Predictive accuracy, as measured by the area under receiver operating characteristics curve (AUC), is a means of estimating the degree of discrimination of a signal detection system and is used as an evaluation metric in this study. We tested our integrative method using the following three different experiments so that we could also explore the effect of data size and bias on the method: (i) where we combined FAERS with a single small-scale EHR database NYP/CUMC, (ii) where we combined FAERS with a large-scale network-based EHR database, and (iii) where we combined FAERS with a much larger-scale claims database. We further evaluated our system under the scenarios that the two resources used in combining to provide consistent/inconsistent information.

Methodology

Data Sources

FDA Adverse Event Reporting System (FAERS)

The data were extracted from FAERS from 2004 to 2010, which comprised case reports mainly reported from pharmaceutical manufacturers and, to a lesser extent, from healthcare professionals and consumers [36]. We preprocessed and mapped the free-text drug names to their ingredient level specification using the STITCH (Search Tool for Interactions of Chemicals) database [37]. The ADRs in FAERS were already coded using MedDRA^® preferred terms [38]. In this study, we did not utilize the explicit relationships between drugs and ADRs and considered all relationships as co-occurrence information. Consequently, we extended data to all medications mentioned in the case reports including primary suspected, secondary suspected and concomitant medications, as well as indications. The signals from FAERS were obtained using the confounding adjustment method, which is presented below.

New York Presbyterian Hospital at Columbia University Medical Center (NYP/CUMC) Electronic Health Record (EHR)

The data were extracted from the single-hospital EHR system at NYP/CUMC, after institutional review board approval. The data consisted of retrospective narrative records of inpatient and outpatient visits from 2004 to 2010, including admission notes, discharge summaries, lab tests, structured diagnosis in the form of International Statistical Classification of Diseases, Version 9 (ICD-9) codes and structured medication lists, and the majority of the data available for this study were from an inpatient population. Narrative reports were used to obtain the patients’ medications, and the structured ICD-9 diagnosis codes were used to detect ADR events; these codes also served as surrogates of patient characteristics for confounding adjustment analysis. Similar to FAERS, the signals from the EHR were computed using the confounding adjustment method proposed in this study.

GE EHR

The EHR database, GE MQIC (Medical Quality Improvement Consortium) (a GE Healthcare data consortium), represents a longitudinal outpatient population, and captures events in structured form that occur in usual care, including patient problem lists, prescriptions of medications, and other clinical observations as experienced in the ambulatory care setting. The data were analyzed systematically under OMOP using seven commonly used methods for 399 drug–ADR pairs [19]. The resulting signal scores are reported and publicly available in OMOP. The signal scores for this database were computed using the optimal analytic method for each outcome as follows: self-controlled case series (SCCS) method for ARF (analysis-ID 1949010), self-controlled cohort (SCC) method for ALI (analysis-ID 409002), and information component temporal pattern discovery (ICTPD) method for AMI and GIB (analysis-IDs 3016001 and 3034001) [19].

Claims Data

In this study, we obtained signal scores associated with the largest claims database—MarketScan Commercial Claims and Encounters (CCAE). Similar to the GE data, CCAE data were extensively analyzed in OMOP for the same drug–ADR pairs with various methods. The signal scores we used for this database were computed by OMOP using the SCC method for ARF, ALI and AMI (analysis-IDs 404002, 403002 and 408013), and the SCCS method for GIB (analysis-ID 1931010) [19].

Reference Standard

The reference standard was developed by OMOP. It contains 165 positive and 234 negative controls, i.e., drugs for which there is or is no evidence for corresponding ADRs. This reference set was established by OMOP based on natural language processing (NLP) of structured product labels, systematic search of the scientific literature, and manual validation. The reference standard comprises 181 drugs and four clinically important ADRs: ARF ALI, AMI, and GIB. More details about the reference standard data collection, including drug names, can be found in a previous publication [39].

Other important research conducted by OMOP resulted in establishment of varied definitions, from narrow to broad, for each ADR outcome they studied [34, 40]. Furthermore, the mapping between ICD-9 codes and corresponding MedDRA^® codes for each ADR outcome were also made available by OMOP. We adopted these definitions to identify ADR case groups in NYP/CUMC EHR and in FAERS.

Cohort Identification

In this study, we used the broad definitions of ICD-9 codes established by OMOP for identifying ADR events in NYP/CUMC EHR [40]. The same definitions were also utilized in the GE EHR and the claims database. In addition, we used the corresponding MedDRA^® codes (as determined by OMOP) for FAERS to identify patients with a particular ADR. Our aim was to ensure that the ADRs are equivalent when using the different databases.

FAERS

Case reports, which have at least one applicable ADR MedDRA^® code for an ADR, were identified as a case group, whereas the rest were used as a control group. The indications and all the medications reported in case reports were included as candidate covariates for confounding assessment.

NYP/CUMC EHR

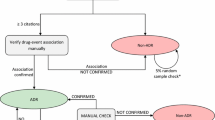
The four ADR case groups were identified using their equivalent ICD-9 codes. For each ADR, the control group consisted of those patients free of the particular ADR. A patient may have multiple records in an EHR and therefore may have experienced an ADR several times, and may have been on and off a particular medication. Only the first occurrence of an ADR was considered and candidate medications were restricted to those that were mentioned before the ADR. If a case patient did not have any medications mentioned before the ADR, or a control patient did not have any medication recorded before 2010, they were excluded from the analysis. We also applied a 180-day window before the latest medication prior to the ADR to retrieve medications and medical conditions (ICD-9 diagnosis codes). We assumed that anything prior to that window was unlikely to be associated with the ADR. For example, a drug taken in 2004 unlikely leads to the development of an ADR in 2010. For the control groups, we used the latest medication record before December 31, 2010 as the anchor, and retrospectively drew a 180-day window to select medications and ICD-9 diagnoses. Since our patient population was dominated by inpatients with single hospitalization, the individual studying windows in the control groups were evenly distributed from 2004 to 2010. Only ICD-9 codes were included as possible confounder candidates. Figure 1 illustrates the data extraction windows for cases and controls.

Fig. 1

Electronic health record (EHR) cohort identification and candidate covariates selection. ADR adverse drug reaction, ICD-9 International Statistical Classification of Diseases, Version 9

Methodology Framework

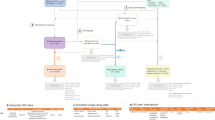
As illustrated in Fig. 2, our methodology comprises three steps: (i) obtaining the confounding adjusted signal score for each drug–ADR pair from individual health data; (ii) calibrating the signal scores based on the empirical distribution derived from a set of reference negative controls; (iii) combining calibrated signal scores from disparate databases. In what follows, we elaborate the technical details in each of the three steps.

Fig. 2

Methodological framework. ADR adverse drug reaction, CCAE MarketScan Commercial Claims and Encounters, EHR Electronic health record, FAERS FDA Adverse Event Reporting System, GE EHR GE Healthcare MQIC (Medical Quality Improvement Consortium) database, NYP/CUMC New York Presbyterian Hospital at Columbia University Medical Center, OMOP Observational Medical Outcomes Partnership

Obtaining Confounding-Adjusted ADR Signal Scores

This step was based on a previously published work conducted by our group which included identifying confounders for specific medications using marginal odds ratios (ORs) and estimating the drug–ADR associations using a least absolute shrinkage and selection operator (LASSO) type regularization [31]. Results showed that the method outperformed the high-dimensional propensity score method, but the resulting false positive rates still exceeded the nominal level [31]. Therefore, we revised the method in two aspects. (1) In the previous work, we only considered the potential confounders that were significantly and positively associated with both the ADR and the medication. We now expanded this list to include medical conditions that were significantly associated with the ADR and medication in either a positive or negative direction. The rationale is that negatively associated conditions could also bias the strength of association. (2) Standard LASSO implicitly assumes a sparse structure in the covariates, and hence tends to select insufficient confounders in high-dimensional regression, which in turn leads to an inflated false positive rate. We adopted a two-step LASSO [41] for a better control of the false positive rate. In the first step, we used the standard logistic LASSO regression to select the confounders that are associated with ADR after accounting for the impact from the drug use. In the second step, we used a weighted linear LASSO regression to select the covariates that are associated with the drug use. We then estimated the conditional association between the ADR and drug adjusting for all the confounders selected in both steps. It is shown that the type I error could be well controlled by including the confounders from both models [41]. Finally, we used one-sided p values of the adjusted log ORs as the signal scores. The details for the two-step LASSO are shown in the electronic supplementary material, Box 1. For GE EHR and claims data, the signal scores (one-sided p values) were generated based on the log relative risks (log RRs) and their standard errors provided by their optimal methods.

Calibrating ADR Signal Scores Based on a Set of Reference Negatives

If there is no drug–ADR association, the signal scores using one-sided p value should be uniformly distributed over the interval (0, 1) in theory. In reality, that is often deviated and leads to an inflated false discovery rate. We apply the estimation algorithm to a set of negative controls in the reference standard, and estimate the empirical distribution of resulting signal scores following formula (1), where q _i represents a one-sided p value of a negative control and n represents the number of negative controls in the reference standard. $\hat{F}_{n} \left( x \right)$ is then used as the null distribution to calibrate signal scores. This calibration was ADR specific by assuming that signal scores within similar groups have their inherent ranking. For example, a negative control for ALI was not considered in the calibration of AMI. This procedure could be considered as a supervised training procedure with the training set consisting of negative controls in the reference standard. Since we did not use the overall reference standard for both training data and testing data, over-fitting is less of a problem.

$$ \hat{F}_{n} \left( x \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} I\left\{ {x < q_{i} } \right\} $$

(1)

Combining ADR Signal Scores from Two Heterogeneous Databases

Let p _i1 denote the ith ADR signal score computed from source 1, for example, the NYP/CUMC EHR, and $p_{i2}$ denote the signal score for the same drug–ADR pair computed from source 2, for example, the FAERS. We used the formula (2) to combine the signal scores from the two data sources.

$$ - 2*\left[ {\log \left( {p_{i1} } \right) + \log \left( {p_{i2} } \right)} \right]\sim \chi_{\left( 4 \right)}^{2}\, {\text{under the null hypothesis}} $$

(2)

Evaluation Design

We used the reference standard developed by OMOP as described above to generate three reference standards for our study. For reference standard 1, we restricted the evaluation to those drug–ADR pairs for which FAERS contained at least one case report and the NYP/CUMC EHR contained at least five patients who were exposed to the studied medications and who were later diagnosed with the studied ADR. The application of a case count threshold is to ensure numeric stability in the signal detection estimates, consistent with what is proposed by Bate and Evans, in the use of PRR (proportional reporting ratio) as signal detection routine for SRS alone [7]. For reference standard 2, we restricted the evaluation to those drug–ADR pairs for which FAERS had at least one case report and the GE EHR had results available in the OMOP result set. We had the same restriction for reference standard 3 based on FAERS and CCAE claims data. The details of these three reference sets are shown in Table 1.

Table 1 Subsets of the OMOP reference standard used in the three experiments

Based on reference set 1, 2 or 3, the performance of the combined system was compared against the performance of signal scores generated by each data source independently. Performance was measured using the AUC. To test if the differences of AUCs based on the different combination systems were statistically significant, we computed a one-sided p value for the hypothesis that the difference between the AUC of the two systems was not equal to 0. The tests were computed using a bootstrapping method [42, 43]. To ensure the p values were computed based on large enough samples of signal scores, and to get a single answer representing all outcomes, the significant tests were based on overall reference sets used in each experiment.

We further studied the nature and proper use of the combined system on the basis of four scenarios that could occur in actual pharmacovigilance practice, and which clinical assessors deal with frequently in their routine work. Using the cutoff p value of 0.05, we defined a drug–ADR pair as a signal if its p value is <0.05. Accordingly, the four scenarios are: (i) a drug–ADR pair has p value <0.05 in both FAERS and healthcare databases meaning a consistent signal is exhibited in both sources; (ii) a drug–ADR pair has p value ≥0.05 in both data sources meaning the lack of this signal in either source; (iii) a drug–ADR signal appears in FAERS but not in healthcare database meaning an inconsistent signal is exhibited; and (iv) a drug–ADR signal appears in healthcare database but not in FAERS, also meaning an inconsistent signal is exhibited.

We also compared the AUC before and after confounding adjustment on the basis of the FAERS and NYP/CUMC EHR, respectively. Furthermore, we identified false positive signals in NYP/CUMC EHR by selecting those negative controls that produced a one-sided p value <0.05 in the confounding adjustment analysis. We identified false negative signals in EHR by selecting those positive controls that had a one-sided p value >0.05 in the confounding adjustment analysis. In addition, we compared the AUC performance of the confounding adjustment method with the cutting-edge method Gamma Poisson Shrinkage (GPS) that produces signal scores signified by lower 5th percentile of the posterior observed-to-expected distribution (EB05) on the basis of FAERS data. We restricted evaluation to those drug–ADR pairs for which FAERS had at least one case report. Furthermore, we assigned a signal score value of 0, the lowest possible signal score for EB05, to those drug–ADR pairs that were never mentioned as primarily suspected relationships, and consequently not included in the analysis using GPS.

Results

We used 2.7 million case reports from FAERS, 0.3 million patients from the NYP/CUMC EHR, 11 million patients from the GE EHR data, and 47 million patients from the CCAE claims data. Some case reports were excluded in FAERS due to typos of drug names and/or the incomplete list of drug names using STITCH. The characteristics of patients for the four databases are shown in Table 2. FAERS has the oldest population while CCAE has the youngest population. The ratio of males to females is approximately 1:1 for CCAE while other databases have more females than males, and among them FAERS has the largest number of females.

Table 2 Demography for four databases

Table 3 shows the AUCs with and without confounding adjustment, which suggests that the confounding adjustment was essential for both FAERS and NYP/CUMC EHR individually. The AUCs after the confounding adjustment in FAERS were statistically significantly better (e.g., higher) than those without the adjustment based on reference set 1. However, we did not observe a substantial improvement in the NYP/CUMC EHR. In total, there were four false positive signals and 35 false negative signals for the NYP/CUMC EHR. We displayed them correspondingly in electronic supplementary material Table S1 and Table S2.

Table 3 AUC for FAERS and NYP/CUMC EHR before and after confounding adjustment

The results from experiment 1 are presented in Table 4. We found that the FAERS system performed significantly better than the NYP/CUMC EHR system. Combining FAERS and NYP/CUMC EHR data did not improve the ADR detection performance of FAERS, although it did not harm it either. The combined system also performed significantly better than the NYP/CUMC alone. Experiment 2, which is also presented in Table 4, shows that the combined system outperformed both the FAERS and the GE EHR individual systems. Improvements were observed for all the outcomes, although at different levels. The AUC of the combined system ranged from 76 % for ALI to 92 % for ARF. For individual systems, the AUC performance of the GE EHR system was better for AMI, but worse for ARF, ALI, and GIB, compared with FAERS. Similar results were found when combining FAERS with the CCAE in experiment 3. The CCAE had better performance than FAERS for AMI and GIB, but was worse for the other two. Again, the combined system outperformed the individual ones for all the four outcomes.

Table 4 AUC of signal detection performance for FAERS, healthcare data, and combined systems

Results in Table 5 show that the combined system achieved better AUC performances in most of four scenarios for two of the combination studies. Overall, the combined system had an increase in AUC when compared to the individual systems where the increase ranged from 3 % to 11 %, but there was one exception. The exception occurred in one scenario where the AUC was higher when using the claims database alone in the situation where the signals were detected in FAERS but not in the claims database. The difference in AUC performance was defined as the AUC of the combined system minus the AUC of the better performing individual system.

Table 5 The AUC performance of FAERS, healthcare data and the combined system on the basis of four scenarios

Using the cutoff p value of 0.05, we evaluated the precision and recall of the two combined systems—the combination system using FAERS and GE EHR, and the combination system using FAERS and claims data. Combining FAERS with the GE EHR resulted in higher recall (0.41 versus 0.35), while the precisions of the two combination systems were almost identical (0.925 versus 0.931). Using the same cutoff p value, eight more signals were only detected by the combined system using FAERS and GE EHR, as shown in Table 6. Among them, seven of the eight were true positive signals.

Table 6 ADR signals detected only using the combined GE and FAERS system and their one-sided p values in three systems

Figure 3 shows the histograms of the signal scores for GIB in each experiment. It is apparent from the figure that the scale of signal score for FAERS did not overlap substantially with each healthcare data set, and the distribution of the signal scores did not follow a normal distribution.

Fig. 3

Histograms of signal scores when combining FAERS with the three healthcare data sets. Signal scores for FAERS and the EHR are signified by log odds ratio, and signal scores for the GE EHR and the claims data are signified by log relative risks. EHR Electronic health record, FAERS FDA Adverse Event Reporting System, GE EHR GE Healthcare MQIC (Medical Quality Improvement Consortium) database, NYP/CUMC New York Presbyterian Hospital at Columbia University Medical Center

Discussion

The main results of our evaluation show that combining signals from two relatively large data sources (e.g., FAERS and the GE EHR data, FAERS and the CCAE claims data) using the proposed methodological framework led to an overall significant improvement, which was replicated for the different outcomes. However, we did not observe the improvement when combining FAERS with the NYP/CUMC EHR. The discrepancies are possibly attributed to issues such as small data size and sample biases.

Small Data Size

NYP/CUMC EHR has already been successfully used for detecting safety signals in several studies [13, 44, 45]. However, challenges remain because of the relatively small size of the data. There were only 0.3 million patients in NYP/CUMC EHR compared with 11 million in GE EHR and 47 million in the CCAE claims data. Since ADRs generally occur infrequently in the EHRs, and their signals are often weak, a large data size is essential for effective detection.

For the same reason, we could clearly observe that higher prevalence of an ADR resulted in better performance on the basis of the NYP/CUMC EHR. Specifically, NYP/CUMC EHR included 14,890 patients with ARF, 6099 patients with ALI, 5817 patients with AMI, and 6683 patients with GIB. ARF, with many more patients (almost three times as many patients as those developing AMI), had better AUC performance than the other three ADRs. Furthermore, when using NYP/CUMC EHR to detect the drugs associated with ARF, we achieved 100 % precision, and successfully identified three true positive medications: hydrochlorothiazide, telmisartan, and candesartan.

Sampling Biases

The NYP/CUMC EHR data came from a tertiary care academic medical center in a major metropolitan inner city area, which may have led to a highly skewed population. In addition, many of the patients included in our analysis could have been referred from other facilities and therefore their EHR data may have been incomplete because it may have lacked longitudinal information for many of those patients. Specifically, only 37 % of patients had at least one outpatient visit and only 14 % of patients had more than one visit. The NYP hospital does have an in-house formulary, which is applicable only to medications concerning inpatients. However, the medications studied in this work were mainly home medications and were not related to the NYP hospital formulary. Moreover, NYP/CUMC EHR data was not linked to pharmacy prescriptions or refills, and the medications extracted from free-text notes were just mentions of medications, and therefore temporal relationships between medication exposures and ADR events may not have been definitive. In contrast, the GE EHR represented a large outpatient population and captured longitudinal patient information, such as ICD-9 coded medical problems and prescriptions. NYP/CUMC represented an inpatient data source and GE EHR represented a strictly outpatient data source, both of which could not capture the complete patient information, and therefore the rates of ADRs might be underestimated. The claims data represented a much larger and more diverse population, and captured longitudinal patient information including diagnosis codes for billing purposes, as well as dates when prescriptions were filled or refilled. However, both the GE EHR and the claims data may also have faced the challenge of a skewed patient population, such as sicker patients having many more visits, and more prescriptions and refills in the database [46].

Usefulness for Pharmacovigilance Practice

The AUC evaluation showed that FAERS had substantially better performance for ARF and ALI, and worse performance for AMI than healthcare data, which indicates that no single source may provide best evidence for all ADR detections. Therefore, synthesis of evidence from multiple streams of information is extremely significant. Currently, clinical assessors carry out the analysis of evidence from multiple sources. For example, clinical assessors may validate or want to evaluate a signal from different resources, such as those generated from SRSs and/or healthcare data. Thus, a common situation that clinical assessors need to deal with is inconsistent or conflicting information from the different data sources.

Results show that the combined ADR signals generated by the proposed method improved the AUC performance significantly compared with individual systems. In addition, we evaluated the combined system in four scenarios mentioned above. We observed that the consistent improvement was achieved by the combined system except for signals that appeared in FAERS but not in the CCAE claims database. However, the combined system was still better than the FAERS system alone in ranking potential signals. Therefore, the proposed system could serve as a tool for clinical assessors when they review ADR cases. For example, in the scenario of consistent signals, clinical assessors are likely to believe the existence of the signals and may want to select the strongest signals for further assessment; the combined system could prioritize signals by integrating the two sources. In the scenario of inconsistent signals, the combined system is able to resolve inconsistent or conflicting statistical information and then provide a single response through the consolidation of statistical information from the two sources. In the scenario where no single source provides a signal, the combined system could possibly transfer two relatively weak signals into a strong composite one. For instance, eight more signals were detected only using the combined GE and FAERS system and seven of them were true positives, which is promising. However, a practical challenge is how to effectively communicate these results to the clinical assessors. In addition, combining FAERS with GE resulted in higher recall and almost identical precision when compared with combining FAERS with claims data. These results further demonstrated that the larger data size (e.g., combining FAERS with claims) does not necessarily lead to more sensitive ADR detection. We also observed that healthcare databases were more sensitive for ADR detection than FAERS in that more signals were identified. We acknowledge that the recall and precision are threshold-dependent performance metrics. Hence, the results may vary when using different thresholds. In practice, pharmacovigilance requires the successful integration of quantitative measures of population-level summaries with clinical adjudication and insights that derive from patient-level case review. The true utility of this approach will only be determined through implementation into the workflow of current pharmacovigilance operations.

Related Work

Our method was designed originally to combine the NYP/CUMC EHR with FAERS, which is the first such study. Harpaz et al. designed an empirical Bayes model to combine signals across FAERS and claims data showing its effectiveness using the same reference standard used in this study [25]. However, that method required that the data satisfy two assumptions: (a) the signal scores generated from each individual data source should be on approximately the same scale, and (b) the scores should follow the log normal distribution. Our data sets did not meet these assumptions. Figure 3 illustrates the violation of the above two assumptions for GIB, but the other three ADRs had similar results.

Methods to Deal with Confounding

The capability to reduce or eliminate confounding is a major aim of ADR detection. Self-controlled designs have recently been proposed and successfully utilized in ADR detection based on longitudinal healthcare data. They attempt to identify equivalent periods of unexposed time within the same patients, against which to compare the same patients’ exposed time. However, NYP/CUMC EHR data lacked this kind of longitudinal information relating to when a patient was put on or taken off a medication. Our prior study showed that insufficient confounder selection led to high false positive rates [31] and therefore we designed the two-step LASSO regression (step 1 of the proposed methodological framework) to select more associated confounders. The AUC performances were generally improved after the confounding adjustment except for ALI. We also applied this algorithm to the FAERS data and the AUC performances were statistically significantly better with this algorithm than without it. Although the proposed confounding adjustment method for FAERS could not leverage primary suspected information stemming from the clinical judgment of the reporter, the results in electronic supplementary material Table S3 show that the confounding adjustment method achieved comparable performance with the cutting-edge algorithm GPS based on primary suspected medication. For example, the confounding adjustment method had better AUC performances in ARF, AMI, and GIB, and lower AUC performance in ALI. We are also aware that clinical assessors in the industry sometimes include concomitant medications in addition to the primary suspected medication in the disproportionality analysis. However, the implications of including concomitant medications in disproportionality analysis, which is not able to deal with confounding by co-medication, are beyond the scope of this paper. The advantage of the two-step LASSO compared with the single LASSO is shown in electronic supplementary material Figure S1 and Figure S2, where the two-step LASSO separated positive controls more from negative ones, reduced the false positive rate, and achieved better AUC performance.

False Positive Signals in CUMC/NYP EHR

One false positive signal was rosiglitazone for GIB. Rosiglitazone was mentioned in the records of 1587 patients where 133 of the patients developed GIB. The confounding adjustment method scored this pair with a one-sided p value of 0.01. In contrast, pioglitazone is in the same drug class, and was mentioned in the records of 2477 patients where 110 patients developed GIB. The confounding adjustment method scored this pair with a one-sided p value of 1.

False Negative Signals in CUMC/NYP EHR

Ryan et al. demonstrated that the cohort method using high dimensional features selected by Bayesian logistic regression generally yielded a negatively biased estimate [19]. We observed the same trend in our data set and summarized possible reasons for false negative signals. (1) Data sparseness since there were not enough patients exposed to the studied medications when the ADR occurrences were quite rare. (2) Confounding by indication because an indication for a drug may bias the estimated association if it is associated with an increased risk of the ADR itself. For example, amlodipine and nifedipine have hypertension as an indication, but hypertension was also related to AMI, and therefore the method did not yield positive associations. However, amlodipine and nifedipine were in the reference standard as being positive for AMI. The proposed method could not deal with this issue correctly, and more clinical knowledge may be needed. For example, we may compare a medication with the other medications in the same treatment regimen to better understand its relationship with the ADR.

Generalization of the Method

The overall method includes three steps, which are (1) generating drug ADR signals, (2) calibrating ADR signal scores based on a set of reference negatives, and (3) integrating calibrated signals. Step 1 and Step 3 are easily generalizable to other ADRs. Step 2 requires the availability of negative controls for a particular ADR, and for ADRs where negative controls are available, the method is generalizable. In addition, the process developed by OMOP, which involves examining and collecting negative controls, is generalizable and could be adapted to other ADRs.

Limitations

This study had several limitations. First, using the NYP/CUMC was a limitation because of its relatively small population, which limited EHR signal detection capability, and therefore performance of the combined system as well. In future work, we plan to include additional EHR data from multiple sites. Second, when using the NYP/CUMC EHR, we simply adopted the OMOP outcome definitions, which may not be optimal for the EHR data set, and could have led to outcome misclassification including both false positive and false negative patients. Third, the confounding adjustment method did not deal well with drugs given only to a particular patient population and therefore the control groups on the basis of a general population were not representative for that population. Fourth, the confounding adjustment method assumed a single and homogeneous OR for a drug–ADR combination, which may not be appropriate. For example, an ADR is more likely to happen among patients who have contraindications or who have certain comorbidities than in other patients. In future work, we plan to apply clustering algorithms to group patients with similar symptoms or diagnoses and then acquire associations within these relatively homogeneous patient groups. Fifth, when using FAERS, we did not remove duplicate reports or correct terminological errors. Lastly, the reference standard consists of test cases that were publicly known during the time frame of our evaluation, and thus the performance may be altered when using the reference standard of emerging safety signals [47].

Conclusions

In this paper, we described a method for ADR detection that combined FAERS with healthcare data and showed significant improvement when individual healthcare resources had sufficient amounts of data. Although the small NYP/CUMC EHR database did not contribute to improvement, use of the large-size network-based GE EHR data and claims data did significantly show improved performance when combined with the FAERs data. An advantage of this method is that it can serve as a tool for synthesizing evidence for clinical assessors in actual pharmacovigilance practice.