FormalPara Key Points

The present work established a relationship between vincristine area under the curve (AUC) and the risk for vincristine-induced peripheral neuropathy (VIPN).

A target AUC of 50 ng⋅h/mL was established to maintain the probability of Grade ≥ 2 VIPN over five dosing occasions below 40%.

Through simulations, the findings suggest that using model-informed precision dosing of vincristine can help lower the chances for VIPN, while simultaneously allowing for dose increments in patients who are less susceptible for VIPN.

1 Introduction

Vincristine is a synthetic vinca-alkaloid drug that restricts tumor growth through interference with intracellular microtubules. The chemotherapeutic agent is used in pediatrics for the treatment of various hematological and solid cancers, where currently doses of 1.5–2 mg/m2 with a 2–2.5 mg dose cap are recommended [1]. For neonates and infants aged < 1 year or bodyweight ≤ 12 kg, vincristine is administered at doses of 0.02–0.05 mg/kg or 0.75–1.5 mg/m2 [2]. Vincristine is often administered in combination with other anticancer agents, with the specific combination depending on the type of cancer being treated.

The main complication of vincristine is vincristine-induced peripheral neuropathy (VIPN), a dose-limiting adverse effect that has been reported in 10–100% of children under current dosing practices [3]. VIPN presents with peripheral and mostly symmetric nerve damage, giving rise to symptoms such as sensory loss, neuralgia, motor dysfunction and constipation. These symptoms often develop after several doses of vincristine and become progressively worse over treatment cycles. In most cases, VIPN fades within a few months after discontinuation of therapy. However, in 16% of childhood survivors, symptoms of VIPN can persist for decades after treatment has ended [4].

Besides the current dose recommendations based on body surface area (BSA), no preventative strategies are in place to reduce the incidence of VIPN and additional measures are symptomatic in nature, mainly using analgesics such as gabapentin, or laxatives in case of constipation. Dose adjustments of vincristine are considered in case of clinically unacceptable toxicity that is an indirect marker for higher toxic sensitivity and an indicator for individual overexposure. Additional measures to dose-adjust based on patient characteristics could help improve individual dose decisions before the occurrence of VIPN.

The pharmacokinetic (PK) profile of vincristine has previously been characterized to exhibit a rapid initial distribution half-life of under 10 min. Previous studies have additionally shown large interpatient variability in vincristine PK, with reported coefficients of variation in clearance (CL) close to 40% [2, 5,6,7,8,9,10,11,12]. Variability in PK parameters, such as CL, may give rise to differences in the risk of experiencing VIPN, since some patients experience higher exposure than others under BSA-based dose strategies. One of the contributing factors to this PK variability is the presence of functional variants in the cytochrome P450 (CYP) 3A5 gene [13]. In the Caucasian population, around 10% of individuals are extensive metabolizers (high expressers), leading to a faster drug metabolism and lower drug exposure [13, 14]. Genotyping could therefore be a valuable tool to comprehend differences in PK resulting from variations in the CYP3A5 gene among patients; however, not all exposure variability can be explained by the CYP3A5 genotype.

Therapeutic drug monitoring (TDM) represents the practice of measuring drug concentration levels and adjusting the individual dosage to arrive within a target exposure window. When PK models are used to calculate a dose based on measured plasma concentrations for each patient, this form of TDM is called model-informed precision dosing (MIPD) [15, 16]. Utilization of TDM or MIPD to guide dose adjustments can be beneficial to minimize adverse effects for drugs with large variability in PK and for which clear PK/pharmacodynamic (PKPD) relationships exists [17]. Indeed, individualized dosing of carboplatin using PK measurements compared with weight-based dosing demonstrated reduced variability in PK and decreased incidence in hematological toxicities in neonates [18].

Nevertheless, the precise relationship between vincristine dose, exposure and VIPN remains unclear. Further characterization can therefore guide the decision to use vincristine exposure as an early biomarker predicting the risk of VIPN. PK and PKPD analyses can quantify the inter- and intrapatient variability in exposure, as well as the relationship between dose, exposure and toxicity, such as the development of VIPN. Furthermore, PK and PKPD models can be applied to perform in silico trials of MIPD, e.g. exploring the impact of age, dosing regimens or CL characteristics on the risk of VIPN.

This study set out to investigate two important prerequisites to improve vincristine dosing. First, to define the PK and PKPD of VIPN, based on a cohort of pediatric oncology patients aged 2–18 years [9]. Second, to evaluate whether TDM based on either non-compartmental analysis (NCA) or MIPD can improve drug exposure to reduce the incidence of VIPN. In silico vincristine dose adjustments were simulated in virtual patients to evaluate fixed dosing as compared with MIPD-based dosing. Based on our findings, we provide practical recommendations and limitations for direct clinical implementation of MIPD for vincristine.

2 Methods

2.1 Patients and Study Design

Thirty-five pediatric patients had been randomized to either receive a bolus (20 patients, 57%) or an infusion (15 patients, 43%) of vincristine [9] (Table 1). Written informed consent was obtained from parents and/or children (if the child ≥ 12 years of age) among those who agreed to participate in this study. The majority of patients (64%) were treated for acute lymphoblastic leukemia (ALL). Standard administration of the infusion was 60 min (38 min vincristine, 22 min flushing), with four patients receiving 96 min (60 min vincristine, 36 min flushing) and two patients receiving a 15-min infusion. Vincristine was administered at the standardized dose of either 1.5 or 2 mg/m2 according to treatment protocol (2 mg dose cap) over several cycles (one to five per patient). Peripheral blood was drawn at 10, 20, 30, 40, 60, 75, 140 min after bolus or start of infusion, and, if the patient remained hospitalized, 24 h after bolus or start of infusion. Genotypes for the CYP3A4 and CYP3A5 genes were not available at the time of execution of the current study. Samples were analyzed using a validated liquid chromatography tandem mass spectrometry (LC–MS/MS) method with a reported lower limit of quantification of 0.1 ng/mL [19].

Table 1 Demographics and covariates of patients [n = 35]
Full size table

VIPN was measured after each drug administration using the National Cancer Institute (NCI) Common Terminology Criteria for Adverse Events (CTCAE) [version 4.03 [20]]. Symptoms were scored as follows; peripheral sensory neuropathy (score 0–5), peripheral motor neuropathy (score 0–5), constipation (score 0–5), and neuralgia (score 0–3). The presence of at least one CTCAE item score to be ≥ 2 was considered to be indicative of VIPN. An independent safety committee monitored the incidence of serious adverse events and did not find any reason to discontinue the study. This study was in compliance with the Declaration of Helsinki and was approved by the local Institutional Review Board (IRB) [ethic code: 2014.268].

2.2 Pharmacokinetic Model

A PK data analysis was performed using a compartmental approach with one to three compartments. PK models were fitted to all individual-level data simultaneously using either the first-order conditional estimation method with interaction (FOCEI) or importance sampling (IMP) in NONMEM version 7.3 (ICON Development Solutions, Ellicott City, MD, USA) [21]. The original PK model [9] was redeveloped as the published model included the administration method (bolus vs. infusion) as a covariate on the intercompartmental CL and peripheral distribution volume, suggesting differences in these parameters between bolus and infusion administrations, which was considered physiologically implausible.

Nonlinear processes, such as saturation of drug elimination or distribution were explored to follow a Michaelis–Menten relationship [22]. Individual lag times for bolus and infusion were estimated using various distributions, e.g. uniform, normal and log-normal, to account for possible delays. We addressed the deviations in infusion duration caused by variation in flushing time by multiplying the documented infusion time by a parameter.

Interindividual variability (IIV) in the structural PK parameters was assumed to be log-normally distributed. Allometric scaling was added using exponents of 0.75 and 1 for the CL and distribution parameters, respectively, while normalizing individual weight by a reference value (70 kg) [23, 24]. Other available covariates (age, BSA and disease type) were additionally evaluated on PK parameters.

Additive and proportional residual error models were evaluated with both original and log-transformed drug concentration data. Separate error models were allowed for measurements after bolus and after infusion administration. Additionally, IIV in residual error was considered to account for possible differences between patients in infusion timing accuracy.

Model selection was driven by quantitative assessments based on the likelihood-ratio test (LRT) for nested models, where a drop in objective function value (OFV) of 3.84 (LRT) or more was considered significant [24]. Visual assessment was additionally performed to evaluate model-fit with prediction-based and simulation-based evaluation graphs [25] using Xpose4 (version 4.7.0) and visual predictive check (VPC) [version 1.2.1] packages in RStudio (version 1.2.5001) [26,27,28].

2.3 Approximation of Non-estimated Factors

Given the relatively low number of patients with measurements over multiple dosages (25.7% had more than two occasions, 14.3% had more than three occasions, and 2.9% had more than four occasions) and the high interoccasion variability (IOV) in the exploratory estimations, each occasion was initially handled as a separate individual during the PK modeling process. The estimated deviations from the population CL value (\({\eta }_{{\text{CLest}}1,ij}\)) in this step were subsequently exported, together with their corresponding standard errors (SEs) [*.phi file in NONMEM], for each ith patient and jth dosing occasion. These values were used as input data (i.e. as dependent variables) in a separate estimation where population values for IIV in CL \(({\upomega }_{{\text{CL}},i}\)) and IOV in CL \({(\pi }_{{\text{CL}},ij})\) were estimated separately (Eq. 1). A shared residual error component \(({\sigma }_{{\text{CL}},ij})\) was added to account for deviations due to the SEs.

$${\eta }_{{\text{CLest}}1,ij} = {\eta }_{{\text{CL}},i} + {\kappa }_{{\text{CL}},ij} + {\upvarepsilon }_{{\text{CL}},ij} \times \mathrm{ SE}$$
(1)

Here, \({\eta }_{{\text{CL}},i}\) represents the individual-specific variability in drug CL, \({\kappa }_{{\text{CL}},ij}\) represents the individual-specific variability at the jth dosing occasion, and \({\varepsilon }_{{\text{CL}},ij}\) represents the measurement error in the observed drug CL values for each ith patient and jth dosing occasion.

Given that the CL of vincristine may differ for low and high CYP3A5 expressers, a mixture model was allowed. Because of the relatively small number of patients, the difference in CL was fixed to a previous estimate (1.87 [13]) and the patient probability of being a high expresser was fixed to 10% [11, 13].

2.4 Pharmacodynamic Model

The PKPD analysis of the categorical VIPN data was performed using a proportional odds model with Markovian elements [29] and the Laplacian estimation method, thereby making the assumption that all categories are affected to the same extent by the predictors.

Since only 3/276 CTCAE scores were Grade 3 or 4 VIPNs, these three observations were combined with Grade 2, resulting in three ordinal categories (i.e. Grade 0, 1 and ≥ 2). The VIPN subscores, i.e. peripheral sensory neuropathy, motor loss, constipation and neuralgia, were initially explored to have shared parameters. Thereafter, subscore-specific parameters were evaluated for statistical significance. The log odds of having a CTCAE score above k for the ith patient and the jth observation was modeled as follows (Eq. 2):

$${\text{logit}}\left(P\left(Y_ij\ge k\right)\right)=\mathrm{ log}\left(\frac{P\left(Y_ij \ge k\right)}{1-P\left(Y_ij \ge k\right)}\right)= {\alpha }_{k}+f(\theta ,x)$$
(2)

where P(Yij ≥ k) corresponds to the probability that the CTCAE grade is greater than or equal to grade k; αk represents the log odds intercept for a score of k or above when f(θ, x) is 0; and f(θ, x) is a function and θ a vector of covariate coefficients describing the effect of the predictors, i.e. drug exposure, for the CTCAE categories. The logit transformation is used to maintain the probability between a value of 0 and 1.

The probability of observing score k can then be retrieved as follows (Eq. 3):

$$P\left(Y_ij=k\right)= \left\{\begin{array}{ll} 1- P\left(Y_ij\ge k+1\right) & {\rm if}\; k=0 \\ P\left(Y_ij\ge k\right)- P\left(Y_ij\ge k+1\right) & {\rm if} \; 0<k<K\\ P\left(Y_ij\ge k\right) & {\rm if} \; k=K\end{array}\right.$$
(3)

P(Yij ≥  k) can be calculated with the inverse of the logit function, i.e. the expit function (Eq. 4):

$$P\left(Y_ij\ge k\right)= \frac{1}{1+ {e}^{-\left({\alpha }_{k}+f(\theta ,x)\right)}}$$
(4)

The exposure-response of vincristine on CTCAE scores was assessed using PK summary values. Drug dose (absolute, BSA-scaled) and drug exposure metrics (Cmax, AUC) were assessed as independent factors driving, both as single and cumulative overdosing occasions, the probability of VIPN. The relationship between drug exposure and the development of VIPN was evaluated as either being a linear or (sigmoidal) Emax function, for example (Eq. 5):

$${\text{logit}}\left(P\left(Y_ij\ge k\right)\right)= {\alpha }_{k}+\frac{E_{\text{max}}*{{\text{exposure}}}^{HILL}}{{{\text{AUC}}50}^{HILL}+{{\text{exposure}}}^{HILL}}$$
(5)

To account for an effect delay or prolonged effects, an effect compartment was evaluated. Model selection was based on significance in the drop in OFV in addition to VPCs.

The influence of the previous state on the probability of the current state was estimated (i.e., Markov elements were explored). The addition of IIV was evaluated on baseline probability and drug effect parameters. A covariate analysis was performed to explore whether part of the variability in response could be explained by the available continuous (age, BSA) and categorical (sex, race, disease) factors.

2.5 Evaluation of Model-Informed Precision Dosing (MIPD) and Non-compartmental Analysis

Using the final PK model, two methods, MIPD and NCA, were evaluated to estimate area under the curve (AUC) for intravenous bolus dosing administration based on three concentration measurements. The PK model simulations included residual error, but no IOV or CYP3A5 distinctions in CL. For MIPD (i.e., model-informed TDM), the optimized sampling times, based on expected parameter precision, were derived with the R-based software PopED (Population Experimental Design, version 0.6.0) [30, 31], using a sampling window between 0 and 24 h (continuous scale) after dosing.

For the NCA approach, the log-linear trapezoidal rule was applied. The timing of the first and third samples were fixed to t = 5 min and t = 24 h (last possible clinical sample time) after dose, while timing of the second sample was selected (0.1–23.9 h) in steps of 0.1 h based on the estimated individual AUCs (\({{\text{AUC}}}_{{\text{NCA}},i})\) that resulted in the lowest mean squared error (MSE) compared with the true/simulated individual AUCs (\({{\text{AUC}}}_{{\text{true}},i}\)) [Eq. 6].

$${\text{MSE}}=\frac{1}{n}\sum_{i=1}^{n}{({{\text{AUC}}}_{{\text{NCA}},i}-{{\text{AUC}}}_{{\text{true}},i})}^{2}$$
(6)

To evaluate the accuracies of NCA and MIPD, a virtual population of 1000 patients was generated. The accuracy was evaluated by comparing the calculated AUC with the true AUC (Eq. 7) [x,i = NCA,i or MIPD,i]. \({{\text{AUC}}}_{{\text{MIPD}},i}\) was defined as AUCMIPD,i = Dose/CLMIPD,I, where CLMIPD,i is the estimated CL for the individual. Similarly, \({{\text{AUC}}}_{{\text{true}},i}\) was defined as AUCtrue,i = Dose/CLtrue,I, where CLtrue,i is the simulated CL for the individual.

$${{\text{Accuracy}}}_{x, i}= \frac{{{\text{AUC}}}_{x, i}}{{{\text{AUC}}}_{{\text{true}},i}}$$
(7)

In consultation with involved clinicians, the maximum acceptable probability for one or more Grade ≥ 2 toxicities was set at 40% over an observation period of five dosing occasions. Simulations using different AUC levels were performed based on 1000 virtual patients to average the random outcomes arising from the probabilistic nature of the model. Finally, the AUC corresponding to an average VIPN probability of 40% over five dosing occasions was selected based on the results.

2.6 Generation of the Target Populations for the MIPD Simulations

Since the majority of patients who received vincristine were treated for ALL, an in silico trial was performed using an ALL population. Probability density curves for prevalence of ALL at ages 1–18 years were derived from the literature for a Caucasian patient population [32]. Individual weight and length values were sampled using available growth metrics from the Centers for Disease Control and Prevention (CDC) [33], stratified by sex. Population L, M and S parameters for both weight and height were collected, where L represents the power in the Box-Cox transformation, M is the median, and S is the generalized coefficient of variation of the values for each age year [34].

A virtual population of 1000 individuals was generated, where the age was randomly sampled from the prevalence distributions. Individual weight and height values were randomly sampled using the designated age category, with a correlation of 0.7 between weight and height [35]. BSA was calculated following the DuBois formula. Individuals received a starting bolus dose of 1.5 mg/m2 of vincristine, with a maximum of 2 mg, over five occasions. Differences in CYP3A5 expression were set to population averages (i.e., extensive/poor metabolizer: 10/90%) and IOV in CL was included.

Vincristine PK profiles were simulated with residual error, and samples were taken from each patient at the optimized times (see Sect. 2.5) at dosing occasions 1–4 to decide optimal dose adjustments for occasions 2–5 using the MIPD approach. Each successive occasion therefore had access to an increasing number of samples. Individual PK samples were fed into the model for estimation of individual estimated drug exposure (AUCest,i). The model used for Bayesian estimation included a typical CL value with IIV, i.e. the model made no distinction between genotype or IOV in CL, in line with the initially developed PK model.

The AUCest,i was subsequently used to inform the MIPD approach. An acceptance range of ± 20% was applied around the target AUC, outside of which the dose was either increased or decreased by 20%. However, the individual true exposure (AUCtrue,i) was used to drive the PD model, in order to recreate a real-life scenario in which PK cannot perfectly be estimated by MIPD. If the exposure was ± 40% outside the target AUC, the adapted dose was calculated by multiplying the target AUC by the estimated individual CL. In addition, to mimic a clinical scenario, dose decreases of 20% were initiated at the following occasion whenever a patient experienced Grade ≥ 2 toxicity, unless dose reductions had readily taken place based on exposure. Similarly, dose increases were only allowed in patients without a history of Grade ≥ 2 VIPN throughout the treatment cycles.

3 Results

3.1 Pharmacokinetic Model

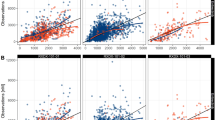
A total of 425 PK samples were available for analysis. A two-compartmental model with linear PK provided a good description of both the bolus and infusion-based data (Table 2; Fig. 1 VPC). Goodness-of-fit plots for conditional weighted residuals (CWRES) for different age and weight groups demonstrate no clear trends versus sampling time or versus population predictions, although there was a tendency of overprediction at the 2.5 h time point for the smaller/younger children (Online Resource 1). Graphical analysis indicated the presence of both a fast and slow distribution phase, however a three-compartmental model could not be identified based on the available data (eight samples after 4 h).

Table 2 Parameter estimates from the final vincristine population PK model
Full size table
Fig. 1
figure 1

Prediction-corrected predictive check of the final vincristine PK model for bolus and 60-min infusion. The solid black circles (•) represent observed vincristine concentrations, the solid red lines (—) are the median of the observed vincristine concentration data, and the dashed black lines (---) are the 10th and 90th percentiles of the observed data. The shaded areas correspond to the 95% confidence intervals for the median, 10th and 90th percentiles based on the simulated data (n = 500). IV intravenous, PK pharmacokinetic

Full size image

A significant improvement in model fit (p < 0.01) was achieved when (1) an individual lag-time was added for bag-to-bloodstream time for the infusion-based observations; (2) a relative increase in infusion duration was estimated for flush time; (3) separate residual unexplained variability (RUV) magnitudes were estimated for the bolus and infusion-based vincristine data; and (4) IIV in the infusion-based residual error was allowed. Statistical significance to estimate separate residual errors for the two administration methods (point 3) and to include IIV in infusion-based residual error (point 4) is due to within-subject measurement error in the infusion-based observations, which was not fully captured by re-estimation of the infusion duration (point 2) [Table 2]. The residual error was modeled as an additive error on log-scale. Besides allometric scaling based on body weight, no covariate was identified to provide a significant improvement of the PK model.

After estimation of the final PK model (Table 2) approximation of non-estimated factors was performed. IOV and IIV in CL based on empirical Bayes estimates (Eq. 1) were similar in magnitude (percentage coefficient of variation [CV%] 36.3 and 32.3, respectively). Allometrically scaled CL for the mixture model’s first group (10%, likely representing fast metabolizers) was estimated at 79.1 L/h/70 kg, compared with 42.3 L/h/70 kg for the second group (90%, likely representing slow metabolizers).

3.2 Pharmacodynamic Model

In total, 276 neuropathy observations were included in the dataset. A proportional odds model with Markovian elements was used to describe the probability of VIPN over time (CTCAE 0, 1 and ≥ 2), using discrete time intervals. Addition of an effect compartment to account for continuous time effects, such as a delay in toxicity or washout time, did not improve model fit. The parameter related to the probability of having a subscore of 1 given the previous score was 0 (B1|0) was shared for all subscores, while it was significant to estimate separate parameters for the probability of transition from 0 to Grade 2 (B2|0) for motor loss and neuropathy, versus constipation and sensory (Table 3). Incorporation of the preceding VIPN observation as a predictor for the following VIPN score (B > 0|Grade > 0, a Markovian element) resulted in the largest improvement in model fit (ΔOFV = 49.6), indicating a higher probability to remain greater than Grade 0 if the preceding measurement was greater than Grade 0. The increased risk for toxicity from the second dose onwards (illustrated by a delay in toxicity in Fig. 2) was accounted for by a different risk parameter for dose occasions >1 (\({\beta }_{k>1}\)) [Table 3].

Table 3 Parameter estimates from the final VIPN population model
Full size table
Fig. 2
figure 2

Visual predictive check for the time course of the probability and severity of VIPN stratified by severity grade (strata = Grade 0, 1 and >1). The black solid lines (—) are the observed time course of the toxicity scores over time, red dashed lines (---) are the simulated median time course of the toxicity scores, and the shaded areas are the model-based 95% confidence interval from the simulations (n = 500). VIPN vincristine-induced peripheral neuropathy

Full size image

With respect to the PKPD relationship, the development of VIPN was most significantly related to the individual vincristine AUC (dose/CL) at each dosing occasion, linked by an Emax function. IIV on the baseline probability, or drug-specific parameters (Emax and AUC50), did not result in a significant drop in OFV (− 0.04 to − 3.6) with estimated variabilities close to zero. None of the evaluated covariates resulted in a significant improvement in model fit.

The predictive performance of the final VIPN model is illustrated by a prediction-corrected VPC (Table 3; Fig. 2). The model-based simulations well described the time course of the probability and severity of VIPN for all CTCAE categories. The simulated number of transitions within an individual was similar to the observed (median observed = 1, median simulated = 1 ± 0.62 standard deviation). The simulated types transitions per occasion were also similar to the observed ones (Online Resource 1).

The relationship between AUC and the probability of VIPN under the different risk scenarios (observation 1, observation > 1, preceding CTCAE = 0 and preceding CTCAE > 0) is depicted in Online Resource 2.

3.3 Optimized Sampling and Target Exposure

Comparison of the two methods to obtain AUC demonstrated higher accuracy and lower bias for MIPD (accuracy = 0.97 [median]; 0.58 [2.5th percentile] − 1.43 [97.5th percentile]) with optimized times of 0.33, 6.5, and 7.5 h, versus NCA (accuracy = 1.33 [median]; 0.84 [2.5th percentile] − 2.45 [97.5th percentile]) with optimized time of 0.6 h (0.083 and 24 h were fixed).

Target AUC was set at 50 ng⋅h/mL, based on the observation that the exposure resulted in a 40% target probability for a VIPN Grade of ≥ 2 at any time over five dosing occasions (Fig. 3).

Fig. 3
figure 3

Probability of CTCAE grade 0, 1 and ≥ 2 VIPN versus average AUC over five dosing cycles. Black dashed line (---) represents a probability of 40% to develop Grade ≥ 2 VIPN (red bars). AUC area under the curve, CTCAE Common Terminology Criteria for Adverse Events, VIPN vincristine-induced peripheral neuropathy

Full size image

3.4 MIPD Simulation

The simulated trial demonstrated a decreased incidence of toxicity during MIPD-based dose adjustments as compared with standard dosing (starting dose 1.5 mg/m2, maximum of 2 mg) [Table 4; Fig. 4]. The incidence of toxicity reduced from 62.1 to 53.9% during the fifth cycle for MIPD-based dosing as compared with fixed dosing. The difference in toxicity between the two groups increased over the treatment cycles. Dose changes between cycles, i.e. dose decreases, dose maintenance and dose increases (only for MIPD), are summarized for both standard BSA-based dosing and MIPD-based dosing (Fig. 5). At least one dose decrease occurred in 81.4% of patients with MIPD (vs. 86.4% for standard dosing) and dose increments were performed in 33.4% of patients over five dosing occasions (no dose increments were allowed for standard dosing).

Table 4 Incidence of Grade ≥ 2 toxicity overdosing occasions with and without MIPD for the pediatric population (1.5 mg/m2/dose, maximum 2.0 mg)
Full size table
Fig. 4
figure 4

Expected toxicity overdosing occasions for the pediatric population (starting dose 1.5 mg/m2, maximum 2.0 mg). MIPD model-informed precision dosing

Full size image
Fig. 5
figure 5

Expected changes in dose following each dosing occasion for BSA-based and MIPD-based dosing of vincristine in the pediatric population. BSA body surface area, MIPD model-informed precision dosing

Full size image

4 Discussion

The PK and PKPD of vincristine in pediatric patients were established to describe the relationship between vincristine dose, exposure and VIPN. The developed models were employed to define a target AUC of 50 ng⋅h/mL and to compare standard dosing with model-informed TDM of vincristine in a pediatric population.

Estimated PK model parameters closely resembled those previously reported for vincristine, although a direct comparison was limited by the fact that earlier studies used BSA to scale for body size rather than allometric scaling using body weight. However, an approximation of our estimated CL to a BSA-scaled CL corresponds to previously published values (23 L/h/m2 vs. 13.7–25.9 L/h/m2) [2, 5,6,7,8,9,10,11,12, 36]. Previous work identified differences in PK parameters between infusion-based and bolus-based dosing regimens [9], suggesting the presence of non-linear distribution processes. However, we did not identify such mechanisms in our models and the differences were explained by unbalanced measurement errors between dose administration types in the recorded infusion time (potentially due to flush time) and sample time (possibly attributable to lag time). Indeed, when a lag time was added, the relative deviation in infusion time was estimated and separate residual errors were applied. No systematic differences in any of the PK parameters could be observed between patients receiving bolus and patients receiving infusion.

In contrast to previous work [5, 8, 9, 12], our PKPD analysis respects both the longitudinal and ordered categorical nature of the VIPN data, which maximizes the data information and increases statistical power [37]. In our PKPD analysis, AUC of the corresponding dosing cycle was identified as the strongest predictor for the development of VIPN at each dosing occasion. Previous statistical analyses, using logistic generalized estimating equations [9] or the Mann–Whitney U test [8], identified that high intercompartmental CL and high Cmax were significantly correlated with VIPN development. However, a similar study investigating the relation between vincristine PK and toxicity identified a significant relationship between AUC and VIPN (established as Grade ≥ 2; Mann–Whitney U test) [38]. While a significant association was established between Cmax and VIPN in our analysis, the correlation between AUC and VIPN exhibited greater strength. When assessing the relationship between the originally estimated AUC [9] and VIPN using the PKPD model, a significant relationship was found, which might be explained by the difference in the linear (logistic generalized estimating equations) versus Emax (proportional odds model) equation in the models. Additionally, our analysis evaluated the relationship between exposure and VIPN for each subcategory separately and distinguished three levels, specifically Grades 0, 1 or ≥ 2. Conversely, the previous analysis [9] considered the combined scores across all subcategories, differentiating only between Grade < 2 and Grade ≥ 2. This distinction in analysis approach might have resulted in increased power in our study to discern the impact of AUC on VIPN.

A target AUC of 50 ng⋅h/mL was defined on the premise that the probability for Grade ≥ 2 VIPNs should be 40% over five dosing occasions. For neonates and infants, a target AUC range of 50–100 ng⋅h/mL was previously recommended to achieve exposures similar to older children [2]. In adults, a target of 60 ng⋅h/mL was proposed to achieve a receiver operating characteristic (ROC) curve > 0.7 for progression-free survival at 2 years after conducting a PK study in 30 newly diagnosed patients treated according to routine practice (PK measurements taken over a median of 1.1 treatment cycles) [8]. However, neither of the two publications took the exposure-toxicity relationship into account. Given the relatively low number of individuals on whom the exposure-VIPN relationship was estimated, it is not advisable to select a target exposure significantly exceeding 50 ng⋅h/mL despite the model-predicted saturation in VIPN risk at higher concentrations (Fig. 3). A joint PKPD analysis of recurrence/survival and safety would be desirable to define a target window.

Derivation of AUC for TDM based on MIPD provided higher accuracy and lower bias as compared with NCA, based on three concentration measurements. MIPD is also preferred due to its lower sensitivity to missing data, capacity to capture multi-compartment PK, interpolation from first and last observation and ability to separate sources of variability (IIV, IOV and RUV) [39]. Particularly the latter will be an issue for regular TDM given the large RUV and IOV for vincristine, although this would also decrease the value of MIPD [40].

The in silico trial of MIPD-based dose individualization resulted in a lower incidence of VIPN (62.1–53.9% after five observations) due to decreases in dose. Simultaneously, MIPD also enabled dose increases in 33.4% of the individuals, which corresponds to a recent vincristine TDM trial [2], suggesting that higher efficacy may be reached in these patients while maintaining an acceptable degree of safety.

Translating our research into clinical practice involves several essential steps [15, 41]. First, vincristine TDM might require additional nurse training. Our optimized design suggests sampling at 0.33, 6.5, and 7.5 h. Following sample collection, model-based estimations should be carried out and dose recommendations should be provided based on each patient's individual PK parameters. This process should be streamlined within the hospital workflow and requires dedicated software, personnel with an understanding of population PK models, and a responsible unit (medical- or pharmacy-based) to translate the results into dosing recommendations [41, 42]. Additionally, a target exposure should be established. This could be 50 ng⋅h/mL based on our findings, or, alternatively, a value could be selected based on the intended benefit/risk balance in treatment outcomes.

Despite the direct relevance for clinical practice, there are some limitations to this work that may hamper direct implementation. Due to the limited number of longitudinal vincristine concentration and toxicity measurements, the influence of IOV in PK is uncertain and extrapolations over multiple dosing occasions should be made with caution. For this reason, we purposely did not include IOV in the performed MIPD trial, although previous work has demonstrated that IOV should be considered in the model to arrive at the most accurate and precise forecasts [43]. Additionally, the exposure-related parameters exhibited limited parameter precision, which can be attributed to the relatively small sample size of patients and exposures far exceeding the AUC50 value. As a consequence, the observed effects approached the Emax closely. Further data collection may enable a more precise estimation of the AUC50 parameter and IOV on CL. Exploration of other PK biomarkers, such as CYP3A5 genotype, would be valuable, but in practice it may be difficult to implement in clinical routine.

5 Conclusion

The current work presents a PK and PKPD framework for vincristine-induced VIPN. Based on an exploratory in silico trial, the work supports the value of MIPD to reduce the incidence of VIPN. Nonetheless, considering the anticipated reduction in VIPN incidence from 62.1 to 53.9%, the clinical significance is relatively modest. The framework can be further adapted for clinical trial design or to support decisions with respect to target dose, population selection, and dose individualization. Data from such clinical trials can be used to improve insight in the dose-exposure-response relationships of vincristine, and further strengthen MIPD of this drug. Lastly, it would be valuable to have an additional exposure-efficacy extension to the framework to account for how differences in PK give rise to differences in treatment response and overall survival [36].