FormalPara Key Points

Of the nine pharmacokinetic models evaluated in a large, real-world data set (N = 2061 patients), two models (Dao, Jacqz-Aigrain) were found suitable for guiding vancomycin dosing decisions for infants and neonates for patients aged 0–52 weeks, defined as producing predictions within a clinically tolerable window for at least 60% of patients for population model predictions.

For preterm neonates, imputing gestational age reduced the accuracy of model predictions.

Despite clinical wisdom suggesting serum creatinine levels are not informative of renal clearance early in life, our results confirm that measured serum creatinine values improve model predictions.

1 Introduction

Dosing in neonate and infant patients is challenged by their dynamic physiology, high inter-patient variability in body size and organ function, and the difficulty in conducting pharmacokinetic (PK) studies in this vulnerable population. Dosing guidelines for this patient population often extrapolate from studies in older paediatric or adult populations, and attainment of pharmacological exposure targets is poor for many drugs [1,2,3]. One approach for improving exposure target attainment is model-informed precision dosing (MIPD), in which doses are tailored to an individual based on their demographic, anthropometric, genetic and/or biomarker information using a PK model [4,5,6]. These model predictions can be tailored to the patient based on drug serum concentrations or pharmacodynamic markers using Bayesian estimation of the patient’s PK parameters [7, 8].

Optimised application of MIPD requires a PK model that adequately describes the drug PK in the intended population [9]. PK models typically explain some of the inter-individual variability using patient-specific covariates. For infants and neonates, maturation and size are key predictors of drug PK. Maturation-related PK variation is usually modelled using age [e.g. postmenstrual age (PMA) or chronological age], and variation related to body size is typically modelled using body weight [10]. Biomarkers of organ function, such as serum creatinine for renally cleared drugs, can provide further patient-specific PK information about a patient [11].

Translating MIPD to clinical care has unique challenges. In addition to errors introduced into the dose selection process through use of a mis-specified PK model, there may be uncertainty or errors in the clinical data fed into the model. For example, in neonates and infants, the precise gestational age (GA) of a patient may be unknown or erroneously estimated [12], yet this information is needed for PK models that use PMA to model maturation. For newborns in the first few days of life, there is conflicting evidence regarding the relationship between serum creatinine and renal function. Serum creatinine at birth is partially reflective of maternal levels due to placental transfer [13,14,15,16,17], yet serum creatinine has still been found to be predictive of kidney function and drug PK during this time period [18,19,20].

Here, we investigate the impact of uncertainty in maturation and serum creatinine on the performance of PK models in an MIPD context, using a large data set of neonatal and young paediatric patients treated with vancomycin. We first compare the ability of nine literature PK models to predict vancomycin serum concentrations. We then repeat this analysis using either the measured values or imputed values for serum creatinine or GA. We interpret these findings in the context of the mathematical structure of these models to relate serum creatinine or PMA to vancomycin pharmacokinetics. Together, these experiments aim to guide model selection decisions for MIPD of vancomycin in infants specifically, but also provide practical clinical guidance for interpretation of PK in infant populations more generally.

2 Patients and Methods

2.1 Ethics

Data forming the basis of this analysis were collected as part of routine health care operations at contracted health care entities, and were deidentified prior to analysis. Therefore, this study is exempt from federal Human Research Subjects regulations as defined in the federal regulations 45 CFR 46.102(f).

2.2 Data Collection

Data were collected retrospectively from data entered into the InsightRX Nova precision dosing platform over the course of routine clinical care at 28 institutions located within the United States of America. These data included patient sex, height and weight; chronological age at the time of the first dose of vancomycin (AGE); GA at birth; serum creatinine measurement times and measured values; serum vancomycin measurement times and measured levels; and the quantity, timing and infusion duration of vancomycin administered. From these quantities, PMA was calculated as follows:

$${\text{PMA}}_{{\left[ {{\text{weeks}}} \right]}} = {\text{AGE}}_{{\left[ {{\text{weeks}}} \right]}} + {\text{GA}}_{{\left[ {{\text{weeks}}} \right]}} .$$

Patient records were included if the patient was < 365 days of age, received at least two doses of vancomycin within a 1-week period, and had at least one vancomycin therapeutic drug monitoring sample collected during that period. Patient records were excluded if medication administration records could not be unambiguously interpreted (i.e., multiple simultaneous doses, dose quantities that could not be converted to milligrams, gaps in dosing > 1 month, vancomycin drug concentrations prior to the first medication administration), if serum creatinine or weight measurements were unavailable or if data entry errors were suspected (e.g., physiologically implausible drug concentrations or covariate values). Some of these data were previously used in a separate model validation study [21]. For patients where GA was unavailable, it was imputed to be 40 weeks. The impact of this imputation was assessed by repeating the analysis for patients for whom GA was known with an imputed GA.

2.3 Pharmacokinetic Analysis

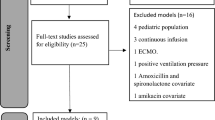
Nine population pharmacokinetic models [22,23,24,25,26,27,28,29,30] were selected from the literature based on availability of covariates in the data set, their suitability for describing pharmacokinetics in neonates and infants, and their current use in MIPD clinical routines (Supplementary Table 1, see electronic supplementary material [ESM]). This was a non-exhaustive literature search, but produced a set of models with considerable variability in model development population size and patient characteristics (Supplementary Table 1, see ESM) and covariate models (Supplementary Table 2, see ESM). All selected models used weight as a covariate. All models except the Germovsek model used serum creatinine as a predictor of vancomycin clearance. All models used either GA or PMA as predictors of clearance, except for the Le model, which was developed on a data set containing children ≥ 90 days old.

These models were implemented into PKPDsim software [31] and are available open-source at github.com/InsightRX/PKPDsim. For each model and for each patient treatment course, drug concentrations were iteratively predicted using maximum a posteriori (MAP) Bayesian estimation as previously described [32]. Briefly, population PK parameters were used to simulate drug concentration–time curves to predict the first drug level for each patient, referred to here as a priori predictions. For subsequent drug levels, MAP Bayesian estimates of PK parameters informed by the first n drug levels were used to predict the (n + 1)th drug level, referred to here as a posteriori predictions. The Jacqz-Aigrain model uses creatinine assay type as a covariate; due to ambiguity in how to implement this covariate based on the publication description, this covariate effect was ignored. Please refer to the supplementary files for R code to reproduce parts of the analysis.

2.4 Impact of Serum Creatinine and Gestational Age on Model Predictions

To assess the impact of inaccuracies in covariate measurements, the iterative prediction process described above was repeated with all serum creatinine lab results replaced with an imputed value (0.3, 0.5 or 0.8 mg/dL) or with a GA of 40 weeks. Only patients for whom GA was recorded were included in the assessment of the impact of imputing GA.

2.5 Statistical Analysis

Prediction precision was evaluated using root mean square error (RMSE), which penalises highly erroneous predictions by squaring residuals. Prediction bias was evaluated using mean percent error (MPE). These metrics were calculated by comparing the iteratively predicted drug concentrations (pred) relative to the measured concentrations (obs) across N concentrations as follows:

$${\text{RMSE }} = { }\sqrt {\frac{{\mathop \sum \nolimits_{{i{ } = { }1}}^{N} \left( {{\text{pred}}_{i} { } - {\text{ obs}}_{i} } \right)^{2} }}{N}} ,$$
$${\text{MPE }} = { }\mathop \sum \limits_{{i{ } = { }1}}^{N} \frac{{{\text{pred}}_{i} { } - {\text{ obs}}_{i} }}{{{\text{obs}}_{i} }}.$$

Clinical suitability was evaluated by quantifying the proportion of predicted drug concentrations that fell within an error margin of 15% or 2.5 mg/L of the measured concentrations. This error margin was determined based on clinical judgment regarding what margin of error may be likely to impact clinical decision making [32], and corresponds to half the width of a target trough range of 15–20 mg/L. Models were deemed to be suitable for clinical use if at least 60% of predictions fell within this error margin for a priori predictions.

Variability in these error metrics was assessed by bootstrapping samples and computing the error metric across these samples. The 5th and 95th percentiles of these error metrics were compared, with overlapping confidence intervals demonstrating statistical significance. For comparison of two distributions, Shapiro tests for normality were performed to assess normality, and parametric or non-parametric tests were used as appropriate.

3 Results

3.1 Patients and Data Collection

There were 2061 patients who met the inclusion criteria (Table 1). Although few of the vancomycin serum levels available (< 5%) were peak samples, defined here as being collected within 3 h of the end of infusion, 32% of the levels were collected 3–6 h post-infusion, which was found to be particularly informative for Bayesian forecasting in adult vancomycin patients [33, 34]. The remaining samples were collected a median of 11 h (range 6–70 h, mean 14 h) after the preceding dose.

Table 1 Summary of patient characteristics across age groups. Unless otherwise indicated, values represent median (range)
Full size table

3.2 Comparison of Model Predictive Performance

Model prediction precision (Fig. 1a) was highest for patients within the first 4 weeks of life using the Jacqz-Aigrain model. For patients aged 5–14 weeks, predictive precision showed less variation across the models evaluated, with the Jacqz-Aigrain model producing the lowest RMSE but statistically significantly lower only compared with the Anderson and Germovsek models. For patients aged 15–52 weeks, the Jacqz-Aigrain model produced the most precise predictions a priori and the Kloprogge model produced the most precise predictions a posteriori.

Fig. 1
figure 1

Model predictive performance by patient age. a Root mean square error (RMSE), b mean percent error (MPE), c proportion of predictions within 15% or 2.5 mg/L of the observed value for the first or second drug level for each treatment course. Variability was assessed across 1000 bootstraps: points indicate the median metric and vertical lines indicate the 5th to 95th percentile of bootstrapped metrics. Solid triangles indicate the lowest (a, b) or highest (c) absolute value for a particular age group. Open triangles indicate values statistically indistinguishable from values marked with a solid triangle.

Full size image

Model prediction bias (Fig. 1b) was lowest for patients aged 0–4 weeks using the Le model for a priori predictions and using the Germovsek model for a posteriori predictions. For patients aged 5–14 weeks, a priori bias was minimised using the Frymoyer model and a posteriori bias was minimised using the Le model. For patients aged 15–52 weeks, a priori bias was minimised using the Germovsek model and a posteriori bias was minimised using the Jacqz-Aigrain model.

As a metric of the clinical impact of these prediction accuracies, we also examined the proportion of predictions that were within 15% or 2.5 mg/L of the measured concentrations (Fig. 1c), error bounds deemed to be appropriate for informing dosing decisions. For patients aged 0–14 weeks, the Dao model was the most suitable for a priori predictions while the Kloprogge model was the most suitable for a posteriori predictions. For patients aged 15–52 weeks, the Jacqz-Aigrain model was the most suitable for a priori predictions while the Kloprogge model was the most suitable for a posteriori predictions. Across all age groups, the Dao and the Jacqz-Aigrain models resulted in prediction accuracies of over 60% for a priori predictions. Accuracy also exceeded 60% for the Frymoyer model for the 5–14 weeks age group and for the Germovsek model for the 0–4 weeks age group.

Overall, the Jacqz-Aigrain and Dao models performed the best in patients 0–4 weeks old. For patients 15–52 weeks of age, the Jacqz-Aigrain and Kloprogge models performed best. For patients between 5 and 14 weeks of age, predictive performance was similar across all but the Anderson model.

The Jacqz-Aigrain model’s good predictive performance in children older than 15 weeks (105 days) was particularly interesting, since it was developed on a data set of patients under 13 weeks of age (Supplementary Table 1, see ESM). One possible explanation is that this model also allows for interoccasion variability, that is, variation in an individual’s PK parameters over the course of therapy.

Given the high proportion of patients for whom GA was not available, the above results were disaggregated according to whether GA was known or imputed (Fig. S1, see ESM). Overall trends between models were similar. Significant differences observed between the imputed and known populations may be due to differences in age distributions between the two groups. The median postnatal age of patients missing GA in the 5–14 weeks age group was 87 days versus 49 days for patients with known GA (Wilcoxon rank sum p value < 0.0001) while for the 15–52 weeks age group the difference in age was 190 versus 177 days (Wilcoxon rank sum p value < 0.01).

3.3 Predictive Value of Serum Creatinine Early in Life

Given the uncertainty in the relationship between neonatal serum creatinine and neonatal renal function, we investigated how informative serum creatinine measurements were for predicting vancomycin pharmacokinetics in patients 0–28 days of age. Iterative predictions were repeated using either measured serum creatinine values or standard values, and error metrics were calculated across age groups selected to capture the biphasic dynamics in serum creatinine over the first 7 days of life, as reported by Allegaert et al. [18]. The Germovsek model was excluded from this analysis since it does not use serum creatinine as a covariate (Supplementary Table 1, see ESM).

For all age groups examined and for all models—except for the Anderson model, which showed poor predictive performance (Fig. 1)—using measured serum creatinine values either minimised prediction errors or was statistically indistinguishable from the imputed serum creatinine value that minimised precision (Fig. 2a) regardless of serum creatinine measurement assay used (Fig. S2a, see ESM). Trends in minimising bias were less clear, and varied by age group and model (Fig. 2b) but not according to reported serum creatinine assay (Fig. S2b, see ESM). For a posteriori predictions, the benefit of measured versus imputed serum creatinine was muted (Fig. S3, see ESM), reflective of MAP Bayesian estimates adapting to moderate covariate model misspecifications by using informative drug concentrations. Together, these results confirm that measured serum creatinine values are informative of vancomycin pharmacokinetics, even in the first few days of life.

Fig. 2
figure 2

Effect of imputed versus measured serum creatinine (CR) by pharmacokinetic model and patient age for a priori predictions. a Root mean square error (RMSE) and b mean percent error (MPE). Variability was assessed across 1000 bootstraps: points indicate the median metric and vertical lines indicate the 5th to 95th percentile of bootstrapped metrics. Imputed CR values are shown in units of mg/dL. Solid triangles indicate CR values with the lowest absolute RMSE or MPE per model and per age group. Open triangles indicate CR values that produce RMSE or MPE statistically indistinguishable from conditions marker with a solid triangle. Number of patients per age group, respectively from left to right: 7, 36, 46, 584

Full size image

3.4 Effect of Imputing Gestational Age on Model Predictions

Although GA or PMA, which is calculated from GA and postnatal age, are consistently found to be predictive of neonatal vancomycin pharmacokinetics (Supplementary Table 1), GA is not always available at the point of care. In these instances, some typical value is conventionally imputed [35]. To assess the impact of imputing GA on predicting vancomycin pharmacokinetics, we compared model predictions made using either the recorded GA or an imputed value of 40 weeks for patients for whom GA was known. The Le model, which uses neither GA nor PMA, was excluded from this analysis.

Prediction error was statistically significantly higher when GA was imputed for patients of PMA ≤ 37 weeks for the Dao, Colin, Frymoyer, Germovsek and Kloprogge models (Fig. 3a). Prediction bias was broadly minimised using recorded GA except for patients with PMA of 37–42 weeks modelled using the Dao or Germovsek models (Fig. 3b). For the patients with PMA ≥ 43 weeks, the impact of imputed gestational age was not significantly different from using the recorded GA. Trends were similar for a posteriori predictions, although the effect sizes of imputed GA were reduced (Fig. S4, see ESM). Together, these results suggest that for patients of PMA ≥37 weeks, imputing GA as 40 weeks is generally suitable in MIPD of vancomycin.

Fig. 3
figure 3

Effect of using patient’s true gestational age (GA) compared with imputing a GA of 40 weeks on model a priori predictive accuracy by pharmacokinetic model and patient postmenstrual age. a Root mean square error (RMSE) and b mean percent error (MPE). Variability was assessed across 1000 bootstraps: points indicate the median metric and vertical lines indicate the 5th to 95th percentile of bootstrapped metrics. Solid triangles indicate a significant difference between imputed and recorded gestational age for the given model and age group. Number of patients per postmenstrual age group, respectively from lowest age to highest age: 334, 449, 218, 336

Full size image

4 Discussion

MIPD holds particular promise for improving drug exposure target attainment in neonatal and infant patients since PK models can account for some of the dramatic interindividual variability through the use of covariates like GA or serum creatinine and through Bayesian forecasting. Here, we compare the predictive performance of nine vancomycin PK models in a large multi-site dataset of patients aged 0–365 days, examining the contributions of maturation and renal function covariates to the predictive performance of these PK models. A strength of our approach is that we iteratively predict the next serum drug concentration using previous levels. This approach assesses model fit-for-purpose for MIPD in clinical practice, in which clinical decisions must be made without knowing future lab results.

We identified the Jacqz-Aigrain and Dao models as clinically suitable for model-informed precision dosing, based on at least 60% a priori predictions falling within a clinically acceptable error margin. We also found that MAP Bayesian estimation of individual PK parameters attenuates the differences in prediction error between different models and between covariate misspecifications. Where a PK model is thought to be a poor fit for a patient, or where uncertainty in covariate values is suspected, clinicians could collect earlier drug levels to improve model prediction precision.

We further found that neonatal serum creatinine, which may partially reflect maternal serum creatinine early in life, still provides valuable information on the neonate’s drug clearance (CL) and improves model prediction precision. Our work here supports the findings by others that serum creatinine concentrations can be interpreted and provide insight into neonate kidney function during the first few days of life [19]. Previously, our group showed that limiting serum creatinine to a minimum value of 1 mg/dL in vancomycin patients over the age of 65 years, a common clinical practice at some institutions, reduces the precision of PK model predictions [36]. Together, these studies provide evidence that observed, unadjusted biomarker values inform and improve pharmacokinetic model predictions, even if the link between these biomarkers and other clinical outcomes is more complex. It underscores the need to consider biomarkers on a per-application basis.

Pharmacokinetic models vary in how they model the relationship between a covariate value and a pharmacokinetic parameter. Figure 4 illustrates the mathematical model between serum creatinine or PMA and CL, holding constant all other covariates, for the nine models investigated here (see Supplementary Table 2 in the ESM for equations describing these relationships). The relationships between serum creatinine and CL plotted in Fig. 4 provide insight into our findings reported in Fig. 2a; models that show high variability in prediction error based on the value of serum creatinine imputed (Anderson, Capparelli) include a strong relationship between serum creatinine and CL in their covariate models. Conversely, models that show little variability in prediction error across values imputed for serum creatinine (e.g., Frymoyer, Colin) include weaker effects of serum creatinine on CL in their covariate models. Similarly, the relationships between PMA and CL plotted here are consistent with Fig. 3, in that the models most sharply adversely impacted by imputing GA (e.g., Kloprogge) include a strong relationship between PMA and CL in their covariate models while those less sensitive to imputed GA (e.g., Jacqz-Aigrain) show a weaker relationship between PMA and CL in their covariate models. Examination of covariate relationships in this way generalises to other drugs and patient populations, for example, to provide clinical guidance in using a model with drug–drug interaction effects or pharmacogenomic effects when a patient’s medical history or pharmacogenomic status is unknown. Small deviations in a PK parameter may not lead to clinically meaningful differences in model predictions or dose selections, while larger deviations in parameter values may indicate that an alternative PK model or dosing algorithm should be selected, or that the clinician should exercise particular caution and collect additional therapeutic drug monitoring samples if feasible.

Fig. 4
figure 4

Relative change in population clearance as a function of serum creatinine (CR) or postmenstrual age (PMA) while holding other covariates constant. To facilitate comparison between models, clearance (CL) was normalised to the value calculated at a CR of 0.5 mg/dL or a PMA of 40 weeks. For the panel on the left, the Germovsek model was excluded because it does not model CL as a function of CR. For the panel on the right, the Le and Capparelli models were excluded since they do not model CL as a function of PMA

Full size image

Clinical guidelines are often based on discrete age categories, but maturation is, of course, a physiologically continuous process. In our analysis here, we found that very young neonate patients (0–4 weeks of age) are best described by one set of models while older patients (15+ weeks of age) are described best by another set of models, with patients in the middle age group showing less clear trends. For patients of PMA ≥ 37 weeks, imputing GA as 40 weeks does not impede model predictive performance. Here, we used a relatively crude method of imputation of GA for patients in which GA was unknown. More sophisticated methods of imputation, such as predicting GA based on birth weight or preterm status, could improve model predictive precision in instances where uncertainty in this covariate may impact clinical decision making [35]. Maturation is typically modelled as a sigmoidal effect on CL (Supplementary Table 2, see ESM), with CL increasing rapidly over the last trimester and first few weeks of life and then tapering off (Fig. 4). Deviations in estimated PMA therefore have a smaller effect on PK parameters as a patient ages.

A limitation of our approach is that we could not assess the ability of the models to accurately estimate area under the concentration–time curve (AUC), the primary drug exposure metric of clinical interest in vancomycin [37]. Without dense sampling, it is not possible to estimate the true AUC experienced by a patient. Here, we assessed the predictive ability of models by their ability to accurately predict the next serum concentration, allowing comparison of a predicted quantity to a known value. We have previously shown that the ability to predict trough concentrations correlates well with the ability to estimate AUCs [21].

5 Conclusion

Overall, this research provides guidance for the selection and interpretation of PK models in MIPD of vancomycin in neonatal and infant patient populations, as well as providing additional insight into the impact of serum creatinine and maturation on pharmacokinetics in neonatal populations more broadly.