Abstract
Hemophilia A and B are bleeding disorders caused by a deficiency of clotting factor VIII and IX, respectively. Patients with severe hemophilia (< 0.01 IU mL−1) and some patients with moderate hemophilia (0.01–0.05 IU mL−1) administer clotting factor concentrates prophylactically. Desmopressin (d-amino d-arginine vasopressin) can be applied in patients with non-severe hemophilia A. The aim of administration of factor concentrates or desmopressin is the prevention or cessation of bleeding. Despite weight-based dosing, it has been demonstrated that factor concentrates still exhibit considerable pharmacokinetic variability. Population pharmacokinetic analyses, in which this variability is quantified and explained, are increasingly performed in hemophilia research. These analyses can assist in the identification of important patient characteristics and can be applied to perform patient-tailored dosing. This review aims to present and discuss the population pharmacokinetic analyses that have been conducted to develop population pharmacokinetic models describing factor levels after administration of factor VIII or factor IX concentrates or d-amino d-arginine vasopressin. In total, 33 publications were retrieved from the literature. Two approaches were applied to perform population pharmacokinetic analyses, the standard two-stage approach and non-linear mixed-effect modeling. Using the standard two-stage approach, four population pharmacokinetic models were established describing factor VIII levels. In the remaining 29 analyses, the non-linear mixed-effect modeling approach was applied. NONMEM was the preferred software to establish population pharmacokinetic models. In total, 18 population pharmacokinetic analyses were conducted on the basis of data from a single product. From all available population pharmacokinetic analyses, 27 studies also included data from pediatric patients. In the majority of the population pharmacokinetic models, the population pharmacokinetic parameters were allometrically scaled using actual body weight. In this review, the available methods used for constructing the models, key features of these models, patient population characteristics, and established covariate relationships are described in detail.
Similar content being viewed by others
Population pharmacokinetic analyses are increasingly performed in hemophilia research. |
In total, 33 population pharmacokinetic models have been retrieved from the literature, describing factor levels after dosing of factor concentrates or desmopressin. |
1 Introduction
Hemophilia A and B are caused by a deficiency of either clotting factor VIII (FVIII) or IX (FIX), respectively [1, 2]. Disease severity is categorized by the patient’s endogenous baseline factor activity level. Patients with severe, moderate, and mild hemophilia have a baseline factor level of < 0.01 IU mL−1, between 0.01 and 0.05 IU mL−1, and between 0.05 and 0.40 IU mL−1, respectively [3]. These definitions of severity are similar for both hemophilia A and B. As patients with severe hemophilia experience spontaneous and more frequent bleeding with development of joint arthropathy and long-term invalidity if left untreated, patients with severe hemophilia and some patients with moderate hemophilia with a severe bleeding phenotype administer factor concentrates prophylactically [4].
In general, prophylactic dosing of factor concentrates in patients with severe hemophilia is targeted at a trough level of 0.01 IU mL−1 [5]. In contrast, factor levels are augmented to physiological levels to maintain optimal hemostasis during a surgical procedure [6]. Following the surgical procedure, higher target trough levels than during the non-surgical prophylactic setting are maintained up to 2 weeks depending upon the type and severity of the surgery, according to current treatment guidelines.
An alternative to factor concentrates in patients with non-severe hemophilia A is desmopressin (d-amino d-arginine vasopressin or DDAVP) [7]. Desmopressin releases von Willebrand Factor (VWF) from Weibel Palade bodies in endothelial cells of the vessel wall. As VWF functions as a FVIII carrier protein, protecting it from proteolysis in the circulation, FVIII activity will also rise upon administration of desmopressin. The reason desmopressin can only be applied in patients with non-severe hemophilia A is that synthesis of endogenous FVIII is required [8].
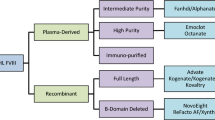
For FVIII and FIX, various plasma-derived (pd) and recombinant (r) concentrate products are available with a standard terminal half-life (SHL). Recently, FVIII and FIX protein molecules have been designed with an extended terminal half-life (EHL) [9]. For both FVIII and FIX, factor molecules have been linked to the Fc domain of immunoglobulin G (rFVIIIFc and rFIXFc) [10, 11]. Other methods to extend the terminal half-life were linking FIX with albumin (rIX-FP) and by PEGylation (N9-GP) [12, 13]. In comparison to SHL products, EHL products of FVIII and FIX exhibit hemostatic activity for longer time periods.
Although factor concentrates are dosed according to a patient’s body weight (BW), it has been demonstrated that FVIII and FIX concentrates show considerable pharmacokinetic (PK) variability [14, 15]. Population PK analyses are increasingly performed in hemophilia research, as constructed population PK models are able to quantify and explain the variability of PK parameters. These studies have provided population PK models that allowed the characterization and comparison of the pharmacokinetics of FVIII and FIX concentrates, and models that can be applied to perform dose individualization and evaluations of limited sampling schedules. Moreover, population PK analyses can assist in the identification of patient characteristics that describe and predict pharmacokinetics [16]. A validated population PK model can be used to perform a maximum a posteriori (MAP) Bayesian estimation to obtain individual PK parameter estimates [17]. The latter estimates are useful to describe the factor level vs time curve for any given dose and help to design individualized dosing regimens. In addition, population PK models allow optimization of clotting factor dosing by an in silico evaluation. In the latter, Monte Carlo simulations are applied that allow the exploration of the resulting factor levels as the dosing regimen or patient characteristics varied [18,19,20].
In this review, the population PK analyses that have been conducted to develop population PK models describing factor levels after administration of FVIII or FIX concentrates or desmopressin are presented and discussed. Moreover, methods used to construct these models, key model features, patient characteristics of studied populations, and established covariate relationships are discussed in detail.
2 Methods
2.1 Search Strategy
To identify the available literature on population PK analyses of FVIII, FIX, and desmopressin in patients with hemophilia A and B, the following PubMed search query was applied: (haemophilia* OR hemophilia*) AND (“VIII”[Tiab] OR “IX”[Tiab] OR “desmopressin”[Tiab] OR “DDAVP”[Tiab]) AND (“population pharmacokinetics”[Tiab] OR “pharmacokinetic model*”[Tiab] OR “Two-Stage*”[Tiab] OR “population pharmacokinetic analysis”[Tiab] OR “population PK”[Tiab]) NOT (“monkey*”[Tiab] OR “mice*”[Tiab] OR “dog*”[Tiab] OR “rabbit*”[Tiab] OR “rat*”[Tiab]) AND (“1960/01/01”[Date—Publication]: “2020/04/30”[Date—Publication]). The last date of publication inclusion was 30 April, 2020.
The retrieved publications were evaluated for eligibility on the basis of title and abstract. From the selected publications, backward citation screening was conducted to identify additional studies from the reference listings. Publications were only selected if they presented a population PK model derived from real-world patient data (i.e., data that are not obtained using Monte Carlo simulations), and were established using either a standard two-stage (STS) analysis or by non-linear mixed-effect modeling (NLMEM). Publications describing non-compartmental PK analyses or population PK models derived solely using simulation techniques, i.e., without real-world patient data, were not included.
2.2 Data Collection
From selected publications, the following data were retrieved: demographics of study population, type of product, laboratory assays used to obtain FVIII or FIX activity levels, modeling software applied, sampling design, other relevant study characteristics related to treatment using FVIII or FIX concentrates or desmopressin, and all presented model parameters.
2.3 Methodology of Population Pharmacokinetic Model Construction
In general, multiple methods can be applied to construct population PK models [21]. However, two methods have specifically been applied in hemophilia treatment. In hemophilia, the earliest population PK models were established using a STS analysis, which is the “traditional” approach [22]. However, currently the most widely used method is NLMEM, which is a one-stage method. The STS and the NLMEM approach both have their advantages and limitations. The complexities and constraints of both methods will, therefore, first be elaborated upon below.
2.3.1 Standard Two-Stage Approach
The application of the STS approach is less time consuming and less complex than the NLMEM approach. The first stage of the STS approach consists of obtaining individual PK parameter estimates for each individual in the studied population using a compartmental model [23, 24]. In the second stage, distributions of these individual PK parameter estimates are described with summary statistics, i.e., the mean and standard deviation of clearance (CL) or volume of distribution (Vd). The values of the means from the parameter distributions represent the population PK parameters, whereas standard deviations represent the inter-individual variability (IIV) for the corresponding parameters.
In this method, it is assumed that each individual from the studied population contributes equally to the estimation of the population PK parameters, although the amount of data may differ between patients. Moreover, the IIV of the population PK parameters is generally overestimated, as the residual error (difference between the predicted and measured factor levels) is included in the IIV for estimating the individual PK parameters [25].
Another drawback of this method is the need for rich data, i.e., ten or more factor levels are required for each individual to adequately estimate individual PK parameters. However, sparse sampling strategies have also been investigated for this method [26]. Essentially, this renders the STS method less suitable for analyzing sparse data, which is often the case in clinical studies.
2.3.2 Non-Linear Mixed-Effect Modeling
Non-linear mixed-effect modeling is a one-stage approach, referred to as the “population” approach [27]. In this method, some or all fixed and random effects enter the model non-linearly, hence the term “non-linear”. The term ‘mixed-effect’ refers to combining fixed and random effects in a single model [28]. Fixed effects comprise typical (median) parameters and parameters describing covariate effects, whereas random effects refer to the parameters describing the IIV or the residual unknown variability. In addition, random effects can also be estimated within an individual (intra-individual variability). For instance, an individual PK parameter may change between occasions using inter-occasion variability (IOV) [29]. An occasion can be defined, for example, as a dosing event or a surgical procedure.
After estimating the IIV and IOV associated with the model parameters, these may be explained using covariate relationships such as the patients’ BW or age. In the covariate analysis, various covariate models may be evaluated for their ability to explain parts of the IIV or IOV. Moreover, the covariate relationships may also be applied to explain a part of the residual unknown variability [28].
In population PK modeling, population parameters are often scaled using the BW of the patients, especially in populations containing both children and adults [30]. By scaling or normalization, a part of the IIV is explained. Although several methods are available to scale model parameters [31], the following equation is generally used for allometric scaling using BW:
in which θTV is the estimated typical value of the population PK parameter scaled to a patients’ BW (BWi), θPop is the estimated population PK parameter value, BWmed is the median of the BW from the studied population (or a value used to scale the population PK parameters such as 70 kg), and EXPBW is the value for the estimated allometric exponent. When fixed allometric exponents are used, a value for EXPBW of 0.75 (or ¾) is used for all clearance parameters, whereas a value of 1 is used for all volume of distribution parameters [32]. These fixed values for the allometric exponents have been derived from biological principles and observations from diverse areas in biology [33]. The allometric exponents may also be estimated empirically, on the basis of the collected data. In that case, the value of exponents may differ from 0.75 and 1 and may differ between the PK parameters.
The NLMEM approach is the most frequently applied method for analyzing vast amounts of population data. However, the application of this method is more complex and time consuming than the STS approach and requires considerable expertise. This method allows simultaneous estimation of both fixed and random effects. Moreover, this method is suitable for analyzing both rich and sparse data, which may be heterogeneously collected between the individuals from the studied population [24, 34]. Similar to the STS method, sparse data impose constraints on the model’s complexity. Therefore, clinical trial design is important to optimally collect data before the modeling process is initiated [35].
3 Results
In the literature search, a total of 132 publications were obtained from which 31 publications describing a population PK analysis were selected. Backward citation screening yielded another two publications [36, 37], providing 33 publications in total.
As either prophylactic (non-surgical) data or perioperative data were used to construct the population PK models, each category is discussed separately. In addition, as population PK models established for FVIII or FIX concentrates can only be applied in patients having hemophilia A or B, respectively, these analyses will also be discussed separately. Below, the methods used to construct the population PK models and their characteristics are elaborated upon.
3.1 Standard Two-Stage Approach
The available population PK models established using STS are shown in Table 1. One population PK model was established using data from a single SHL-FVIII product, whereas the other population models were constructed using combined data from multiple SHL-FVIII products. In one report, the administered product was not specified [38]. The population PK analyses conducted using the STS method are currently of limited clinical value as most of the products that were investigated in these analyses are currently rarely used. Moreover, the models were constructed using sparsely sampled data, which may have hampered the adequate estimation of the IIV associated with the population PK parameters from these models.
3.1.1 Prophylactic Population Pharmacokinetic Factor VIII Models
In two studies, STS analysis was conducted to establish three prophylactic population PK models for several FVIII products (Table S1 of the Electronic Supplementary Material [ESM]) [39, 40]. In both studies, a one-compartment model was used to describe the time profile of FVIII activity after the administration of the dose. In Ruffo et al., population PK parameters were derived for 27 patients with hemophilia A [39]. In Messori et al., two population PK models were constructed using data of single-dose curves from 56 patients and multiple-dosing curves from 32 patients, having either a FVIII dose to treat a minor bleeding episode or a prophylactic FVIII dose, respectively [40].
In the studies by Ruffo et al. and Messori et al., similar values were observed for CL and Vd after administration of a single dose (Table 1) [39, 40]. Moreover, CL (3.93 mL h−1 kg−1) and Vd (61.8 mL kg−1) after administration of a single dose were comparable to the CL (4.14 mL h−1 kg−1) and Vd (53.8 mL kg−1) after multiple dosing.
3.1.2 Perioperative Population Pharmacokinetic Factor VIII Models
Two population PK models were established using STS analysis based on FVIII activity data obtained perioperatively subsequent to dosing of the FVIII concentrate (Table S2 of the ESM). During and after a surgical procedure, the elimination of FVIII may be higher prior to the surgery owing to consumption of the factor concentrate. Therefore, Longo et al. investigated whether a PK model with time-dependent elimination performed better than a model with constant elimination when describing the FVIII levels in 20 surgical patients [37]. The time-dependent elimination was described as follows:
where K is the first-order time-dependent elimination rate constant, Kin is the initial value of K at start of surgery, Kfin is the final steady-state value of K at time infinity, Kvar is the change of K over time, and tas is the time after surgery [38]. After the surgical procedure, the elimination rate constant decreases from Kin to the final steady-state value Kfin. A one-compartment open model comprising the time-dependent elimination rate constant is subsequently used to describe the time profile of FVIII activity.
For ten patients, this model was used to estimate their individual PK parameters. The mean for the calculated early postoperative CL was higher (5.67 mL h−1 kg−1) than the mean of the final steady-state CL (3.05 mL h−1 kg−1), demonstrating the time dependency for CL [37].
The estimated population PK parameter values for the Vd were similar for the constant-elimination one-compartment model (64.7 mL kg−1) and the time-dependent elimination model (65.0 mL kg−1), whereas the value obtained for CL using the constant-elimination model was lower than the values for early post-operative CL calculated using the time-dependent elimination model: 4.87 mL h−1 kg−1 vs 5.67 mL h−1 kg−1, respectively. Although the time-dependent elimination model was only appropriate in ten from 20 surgical patients, the latter suggests that surgical patients may actually have a higher CL during surgery than after a surgical procedure.
Ruffo et al. also performed a population PK analysis of FVIII during surgery using the STS approach. In their study, the value for Vd was comparable to the value observed by Longo et al. [37, 38]. In Longo et al., the estimated values for the elimination rates from Eq. 1 were presented as half-lives, whereas Ruffo et al. presented rate-constant values. When the terminal half-life reported by Longo et al. (9.6 h) is recalculated as the rate-constant Kin, a value (0.072 h−1) was found that was comparable to that of Ruffo et al. (0.071 h−1).
3.2 Non-linear Mixed-Effect Modeling
Non-linear mixed-effect modeling allows the assessment of all model parameters more accurately than an STS analysis [25]. In total, 29 population PK models of FVIII, FIX, and desmopressin have been published (Table 2). The most applied software was NONMEM [41, 42]. In a single case, SAS was applied, which uses a comparable minimization algorithm to estimate model parameters as NONMEM [43]. In two cases, MONOLIX was used, which performs a stochastic approximation expectation–maximization routine [44]. The most important findings of the published population PK models and their covariate relationships are discussed below. The models were categorized according to disease (hemophilia A or hemophilia B), setting (prophylactic or perioperative), and product (SHL, EHL, or desmopressin).
3.2.1 Hemophilia A
3.2.1.1 Prophylactic Population Pharmacokinetic Factor VIII Models
Standard Half-Life Factor VIII Products In 10/16 publications, a population PK model was described for one specific SHL-FVIII concentrate, whereas in one study, data from multiple products were combined (Table 2). In the majority of the population PK analyses, data from both pediatric (aged < 18 years) and adult patients with hemophilia A were combined and analyzed simultaneously. Consequently, PK parameters had to be normalized to reduce the IIV caused by differences in body size. In general, actual BW and lean body weight (LBW) were used to allometrically scale the population PK parameters. Normalization of the PK parameters by BW or LBW explained the IIV considerably. For example, in the study from Karafoulidou et al., allometric scaling reduced the unexplained IIV of CL from 47.8 to 38.9% [45]. The reported half-lives from SHL-FVIII products generally have a range of 11–16 h [46].
Children have a higher FVIII CL per kilogram BW than adults and, therefore, a shorter terminal half-life of FVIII [14]. In 14/16 models, the effect of age on CL was evaluated in the covariate analysis (Table S3 of the ESM). From 16 population models describing the pharmacokinetics of SHL-FVIII, nine studies identified age as a covariate associated with CL [14, 47,48,49,50]. Although age and BW are correlated, incorporation of an association between age and CL improved the model even when PK parameters were normalized by BW. In two of eight models, the allometric exponent on CL was estimated instead of fixed, which allowed an estimation of the empirical correlation between BW and an individual PK parameter [14, 50]. The effect of age on CL in the eight population PK models was considerable, from an age of 1 year, CL decreased between 0.45 and 1% per year until the age of 73 years. However, the effect of age was not always included as a monotonic (linear) relationship, as piece-wise linear models were used as well. A piece-wise linear model allows first to increase CL linearly with increasing age and, subsequently, after a set cut-off point, CL may decrease while age increases. As only eight of 16 studies identified the effect of age on CL, this effect may be too small to be easily identified. Moreover, collinearity between age and BW may further complicate the estimation of this effect.
Other covariates associated with the pharmacokinetics of SHL-FVIII were having an human immunodeficiency virus-positive status, the race of the patient, and the presence of inhibitors (> 0.6 BU mL−1). V1 was 36% higher for patients who were human immunodeficiency virus positive than for patients who were human immunodeficiency virus negative [45]. These patients may, therefore, need higher loading doses. Abrantes et al. showed a significant correlation between the Vd of the peripheral compartment and race [49]. In addition, only Abrantes et al. included patients having FVIII neutralizing inhibitors, present in 45 of 754 patients (6%). As expected, CL may be up to 166% higher when inhibitors are detected. However, this association has little clinical relevance for dose individualization, as patients with high titer neutralizing inhibitors will generally not be treated with FVIII concentrates.
Extended Half-Life Factor VIII Products Although multiple EHL-FVIII products are currently available [51], only three population PK analyses have been reported (Table S4 of the ESM) [52,53,54]. Extended terminal half-life-factor VIII exhibits half-lives longer than those of SHL-FVIII concentrates with values from 14 to 19 h [9]. In the population PK model of Nestorov et al., only the central Vd was allometrically scaled using the patients’ BW. In the covariate analysis, a significant negative association between the level of VWF and CL was identified [55]. As a result, an increase in VWF levels will lead to a decrease in the estimate for CL. Moreover, hematocrit was found to be negatively associated with V1. In the final model, the remaining (unexplained) IIVs for CL and V1 were 25.1% and 13.6%, whereas the IOVs were 22% and 9.3% for CL and V1, respectively.
In the population PK analysis from Chelle et al., both the one-stage assay and chromogenic assay were used to obtain measured FVIII levels [54]. As there may be discrepancies between the results from these assay methods, a correction factor was included in the model [56]. This allowed the use of both types of assay to derive the model parameters with the data from both types of assay simultaneously.
3.2.1.2 Perioperative Population Pharmacokinetic Factor VIII Models
Only one population PK model has been published in the perioperative setting (Table S6 of the ESM), for patients with severe and moderate hemophilia A [57]. This population model was constructed using data from various pdFVIII and rFVIII products. As target levels are augmented to physiological levels to maintain hemostasis during the surgical procedure, these models are able to describe higher FVIII levels than in the prophylactic setting.
In the study by Hazendonk et al., the population PK parameters were allometrically scaled using BW with fixed exponents for CL terms (0.75) and volume terms (1.0) [57]. The CL from patients having blood group 0 was increased by 26% [58]. Patients having a major surgical procedure had a 7% lower CL. Moreover, age was negatively correlated with CL and V1. In contrast to the perioperative population PK models established using a STS analysis, no time-dependent CL parameter was included in the final model.
3.2.1.3 Perioperative Population Pharmacokinetics of Factor VIII after Dosing of Desmopressin
For FVIII levels after desmopressin administration, a population PK model was constructed in 128 patients with non-severe hemophilia A (Table S5 of the ESM) [59]. Included patients received a standard intravenous or intranasal dose of desmopressin. A two-compartment population PK model was constructed with first-order absorption to describe the rate of FVIII response after desmopressin administration. As no actual FVIII was infused and the dose of desmopressin in each patient was set to unity, all PK parameters are apparent parameters. Nevertheless, this model is able to describe the increase and decrease of FVIII over time after administration of desmopressin. In the base model (i.e., the structural model without covariates), considerable IIV was present in the endogenous FVIII baseline (81%), CL (86%), and V1 (67%). In the covariate analysis, this IIV could partially be explained by the most recently measured FVIII level, which was positively correlated to the individual estimated endogenous FVIII baseline and the underlying mutation. Furthermore, a negative correlation was demonstrated between the most recently measured FVIII activity and CL and V1. These associations contribute to the higher exposure to FVIII after administration of desmopressin in patients with the higher most recently measured FVIII levels. Incorporating these covariates in the population model decreased the IIV of the endogenous FVIII baseline, CL, and V1 by 44%, 36%, and 17%, respectively.
3.2.2 Hemophilia B
3.2.2.1 Prophylactic Population Pharmacokinetic Factor IX Models
Standard Half-Life Factor IX Products Factor IX is a smaller protein (55 kDa) than FVIII and, therefore, distributes more easily to the interstitial fluids [46]. Moreover, FIX binds rapidly to type IV collagen on endothelial cells in the extravascular compartment, resulting in a higher inter-compartmental CL (Q2) for FIX than for FVIII [60]. This may explain why all population PK models for SHL-FIX concentrates, except for the model from Suzuki et al., comprised three compartments (Table S7 of the ESM) [15, 61,62,63]. For rFIX products, the half-lives have a range of 18–24 h, whereas the half-lives from pdFIX have a range of 29–43 h [64]. Not surprisingly, the two population models constructed using rFIX data were based on data from a single product as only one rFIX product was available [65]. The two population PK models established using pdFIX data were based on data from various pdFIX products.
In all four published population PK models, the population PK parameters were allometrically scaled using the patients’ BW. In Suzuki et al., the allometric exponents were estimated [63]. In the other models, all exponents were fixed to 0.75 for CL terms and 1.0 for Vd terms. For all models, markedly high IIV (> 19) was associated with the population PK parameters CL (19–36.8%), V1 (19–46%), V2 (28–97.4%), and V3 (19–33.2%). Moreover, in all studies, except for Björkman et al., considerable IOV (range) was estimated for CL (15–48.8%) and V1 (12–47.2%), allowing the corresponding parameters to change between dose administrations within an individual [15, 62, 63].
Although all population PK analyses conducted for the SHL-FIX products investigated the relationship between age and CL, none of the studies included age in their final model [15, 61,62,63]. However, one study identified age as a significant covariate relationship for the volume of the second distribution compartment [61]. Two population PK models described the measured FIX levels after dosing of pdFIX products [15, 62]. Although CL differed between different pdFIX products in both models, only Björkman et al. established a significant covariate relationship, allowing CL to be 16% lower for one brand of the administered pdFIX products [15].
In none of the population PK analyses, conducted for the SHL-FIX products, data from both pdFIX and rFIX products were combined (Table S7 of the ESM). In Björkman et al., the values for CL and steady-state Vd (Vss) from the population PK analyses for pdFIX and rFIX were compared [64]. The typical value of CL obtained for pdFIX products (286 mL h−1) is almost half the typical value for the CL of rFIX (564 mL h−1), demonstrating the more rapid CL of rFIX products. Moreover, the value for Vss was considerably higher for the rFIX products (14.2 L) than for the pdFIX products (9.0 L).
Extended Half-Life Factor IX Products For each of the three EHL-FIX products that are currently available, population PK analyses have been conducted (Table S8 of the ESM). The population median half-lives obtained for these three EHL-FIX products had a range of 82–102 h [9]. The population PK models for N9-GP and rIX-FP comprised two compartments, whereas a three-compartment model was used to describe FIX levels after rFIXFc administration (Table S8 of the ESM) [66,67,68]. A remarkable difference was obtained for the estimate of IIV from Q2 between the population PK analyses for Refixia and Alprolix. While in the population PK analysis conducted for Alprolix an IIV for Q2 of 37% was estimated, a value of 127.3% was obtained in the population PK analysis for Refixia. The latter may have resulted from the small number of patients (n = 15) used to perform the population PK analysis.
Although multiple covariates were investigated by Zhang et al. and Diao et al., only BW was found to be significantly correlated to CL and V1 [66, 68]. As a result, allometric exponents were estimated for CL and V1.
For a 70-kg patient, the estimates of CL from Refixia, Idelvion, and Alprolix were 47.8 mL h−1, 57 mL h−1, and 234.7 mL h−1, respectively, whereas respective values for the Vss were 6265 mL, 8060 mL, and 19,503 mL. In comparison to the estimates for Vss from the SHL-pdFIX products (9.0 L) and SHL-rFIX (14.2 L), the estimates from Refixia and Idelvion were lower, whereas the estimate for Alprolix was higher [64].
3.2.2.2 Perioperative Population Pharmacokinetic Factor IX Models
For perioperative administration of FIX in patients with severe and moderate hemophilia B, only one population PK model was developed (Table S9 of the ESM) [69]. The model was constructed using data from 118 patients undergoing a total of 255 surgical procedures. The population PK model described dosing of various pdFIX products and one rFIX product. A three-compartmental model was established with IIV estimated for CL and V1.
In this analysis, all model parameters were allometrically scaled using similar fixed exponents for all CL terms (0.75) and all Vd terms (1.0). The age of the patients was significantly related to CL and V1 using a linear relationship. For an age below 34 years, the BW-normalized CL and V1 were decreased with 0.89% and 1.15% per year. Above 34 years, no differences were obtained for the BW-normalized CL and V1.
For patients using a pdFIX product, the typical values for CL and V1 were 11% and 17% lower than for a patient using rFIX, respectively. In addition, for patients with moderate as opposed to severe hemophilia B, the typical value for V1 was 10% lower. Remarkably, the estimate obtained for CL from rFIX (564 mL h−1 70 kg−1) in the prophylactic setting was almost twice as high as the CL estimates for rFIX in the surgical setting (284 mL h−1 70 kg−1) [64]. Although this contradicts what was expected, an explanation for this effect is unknown. For pdFIX, less difference was demonstrated, as the estimate for CL in the non-surgical setting (286 mL h−1) was slightly lower than the CL estimated in the surgical setting (252 mL h−1 70 kg−1) [64].
4 Discussion
In this review, all available population PK models describing FVIII and FIX activity or desmopressin after dose administration were summarized. In total, 33 population PK models were retrieved from the literature. In 29 population PK analyses, the NLMEM approach was applied, whereas in four population PK analyses, the STS approach was performed. The latter four analyses described administration of SHL-FVIII only. Moreover, with the advent of NONMEM, this is currently the preferred software to established population PK models. Only one population PK model was developed to describe FVIII levels after administration of desmopressin. From all available population PK analyses, 27 studies also included data from pediatric patients. In total, 18 population PK models were established on the basis of data derived from a single product, whereas the remaining models were established using data from multiple products.
In a minority of the population PK models, IOV of the population PK parameters CL or V1 was described. In three of the four population models describing the pharmacokinetics of SHL-FIX concentrates (Table S7 of the ESM), IOV ranged considerably from 15 to 48.8% and 12–47.2% for CL and V1, respectively. As a consequence of IOV, CL and V1 differ with every dose administration. In a MAP Bayesian analysis, individual PK parameter estimates can still be obtained for population PK models having IOV associated with a population PK parameter [70]. Using the individual PK parameters, individualized doses of FVIII or FIX concentrates can be calculated. Dose calculations based on individual PK parameters obtained with a MAP Bayesian analysis will compensate for the IIV only. If a MAP Bayesian analysis is iteratively applied with the most recent measured factor level, the resulting individual PK parameter estimates will gradually represent the average for the parameter value of an individual. Therefore, despite administration of individualized doses obtained using (iterative) a MAP Bayesian analysis, the resulting factor levels may vary still depending on the extend of IOV. Therefore, one should be cautious when the IOV considerably exceeds the extent of IIV associated with one or more PK parameters from a population PK model used to perform dose individualization.
Several studies have indicated that CL of FVIII immediately after a surgical procedure may be increased because of consumption of FVIII [71,72,73]. To address this change in FVIII CL during and after surgery, population PK models were constructed allowing the CL to change after the surgical procedure (Table 1) [37, 38]. In the study from Longo et al., the time-dependent elimination model allowed a better description of the measured FVIII levels than the constant elimination model in ten out of 20 patients [37]. These population PK models were constructed using the STS approach only. Although Hazendonk et al. evaluated different relationships allowing the prediction of a time-dependent CL in their perioperative population PK model constructed using NLMEM, no time dependence of CL was observed [57]. In a recent study, Preijers et al. did not observe changes over time in the PK parameters during perioperative dosing of FIX concentrates (Table S9 of the ESM) [69]. Whether population PK models constructed using NLMEM allow the description of time-dependent PK parameters in the surgical setting remains to be further studied in prospective studies having well-timed samples before, during, and after surgery [74].
In the majority of the population PK models, the population PK parameters were allometrically scaled using the actual BW. Only in two cases was LBW used for scaling (Table S3 of the ESM). The allometric exponents can be fixed to a value that is set before the relationship is evaluated (“3/4 rule”) or can be estimated [32, 75]. However, if allometric exponents are estimated, the allometric scaling is not based on biologic principles but rather based on statistical heuristics driven by an empirical relationship present in the collected data used to construct the model. As a result, obtaining values for the estimated exponents may be influenced by confounding factors. When the allometric exponents are not accurately estimated, potential issues may arise when the model is used for extrapolation to other populations, such as from adults to children [76]. Moreover, allometric exponents may not be accurate for obese patients if they were not present in the data used to construct the model, as FVIII and FIX are not likely to distribute to the fatty tissue. Nevertheless, the population PK models may be applied to describe the FVIII or FIX levels after administration of a factor concentrate for their corresponding study populations. When applying these models in Therapeutic Drug Monitoring, they should have been validated using independent datasets.
In the majority of the population PK models summarized in this review, the endogenous baseline factor level of the patients with hemophilia from the studied populations was taken into account (Tables 1 and 2). Different methods were applied to correct the predicted factor levels using the endogenous baseline level. Moreover, if the patients used prophylactic doses previous to the loading dose from which, subsequently, the FVIII or FIX levels were measured, a residual pre-dose factor level may be present next to the endogenous baseline level. A correction for the endogenous baseline level may also be performed prior to the initiation of the modeling process. It is important to correct the predicted factor levels using the residual or endogenous baseline levels, as doing not so will affect the estimation of the model parameters [77]. Not correcting for a residual pre-dose or baseline factor level may result in underestimation of Vd and/or overprediction of CL [78]. Therefore, the endogenous baseline factor level and the residual pre-dose factor level should be taken into account when a population PK model is constructed at least for patients with non-severe hemophilia.
When performing patient-tailored dosing using a MAP Bayesian analysis, the availability of a population PK model is a prerequisite. However, if a model contains a covariate relationship, a covariate value must be supplied to calculate the typical value for the corresponding population PK parameter. In a MAP Bayesian analysis, empirical Bayesian estimates are obtained for the model parameters containing IIV or IOV. Using the typical values and empirical Bayesian estimates, the individual PK parameters can be calculated. In the majority of the population PK models summarized in this review, the model parameters were allometrically scaled. In one population PK analysis, the levels of VWF and hematocrit were also associated with covariate relationships to population PK parameters (Table S4 of the ESM). In that case, these VWF and hematocrit levels have to be measured or, if measurements are unavailable, imputed before the individual PK parameters can be obtained accurately. The requirement of extra laboratory measurements poses a limitation for obtaining patient-tailored doses using a MAP Bayesian analysis. Nevertheless, taking covariates into account could improve the selection of the right dose for the right patient and, therefore, all covariate relationships that are likely to have a predictive ability should be evaluated in the construction of a population PK model.
For the majority of the established population PK models, parts of the IIV were explained using covariate relationships. Still, there is considerable unexplained IIV present in most of the population PK models with ranges of 17–50% and 8–54.2% for CL and V1, respectively. Further research may explain the extent of explained IIV. Only a minority of the established population PK models has been applied successfully to perform individualized dosing of factor concentrates [79]. Although the established population PK models are validated internally using the same data set used to construct the model, only a limited number of external validations have been conducted comprising an independent data set [80]. As the latter is considered to be the most stringent approach for model evaluation, such studies must first be conducted before the population models can be applied standardly into clinical practice. Therefore, to allow the application of the established population PK models in clinical practice to obtain individualized doses, further studies have to be performed to validate these models. Currently, various ongoing studies are investigating individualized dosing using population PK models in patients with non-severe hemophilia A (DAVID study) [81], surgical patients with hemophilia A (OPTI-CLOT) [74], and in patients using extended terminal half-life FVIII and FIX products (Target Study).
5 Conclusions
In total, 33 population models describing the pharmacokinetics of FVIII and FIX concentrates and desmopressin are currently available. Four population PK models were established using an STS analysis, whereas the remaining models were constructed using NLMEM. In the majority of the available population PK models, allometric scaling of the model parameters was applied using the BW of the patients. In general, there were two methods applied to take the endogenous baseline or residual factor level in patients with non-severe hemophilia prior to a loading dose into account. Only a minority of the population PK models was successfully evaluated to obtain patient-tailored dosing of factor concentrates. Moreover, only a limited number of the available population PK models have yet been externally validated. As population PK models are increasingly applied to perform dose individualization in clinical practice, further studies are paramount to validate this application.
References
Konkle BA, Huston H, Nakaya Fletcher S. Hemophilia B. In: Adam MP, Ardinger HH, Pagon RA, Wallace SE, Bean LJH, Stephens K et al., editors. GeneReviews®. Seattle (WA): University of Washington; 1993.
Konkle BA, Huston H, Nakaya Fletcher S. Hemophilia A. In: Adam MP, Ardinger HH, Pagon RA, Wallace SE, Bean LJH, Stephens K, et al., editors. GeneReviews®. Seattle (WA): University of Washington; 1993.
Blanchette VS, Key NS, Ljung LR, Manco-Johnson MJ, van den Berg HM, Srivastava A, et al. Definitions in hemophilia: communication from the SSC of the ISTH. J Thromb Haemost. 2014;12(11):1935–9. https://doi.org/10.1111/jth.12672.
Knobe K, Berntorp E. Haemophilia and joint disease: pathophysiology, evaluation, and management. J Comorb. 2011;1:51–9. https://doi.org/10.15256/joc.2011.1.2.
Iorio A, Iserman E, Blanchette V, Dolan G, Escuriola Ettingshausen C, Hermans C, et al. Target plasma factor levels for personalized treatment in haemophilia: a Delphi consensus statement. Haemophilia. 2017;23(3):e170–e179179. https://doi.org/10.1111/hae.13215.
Hazendonk H, van Moort I, Mathot RAA, Fijnvandraat K, Leebeek FWG, Collins PW, et al. Setting the stage for individualized therapy in hemophilia: what role can pharmacokinetics play? Blood Rev. 2018;32(4):265–71. https://doi.org/10.1016/j.blre.2018.01.001.
Morfini M, Coppola A, Franchini M, Di Minno G. Clinical use of factor VIII and factor IX concentrates. Blood Transfus. 2013;11(Suppl. 4):s55–63. https://doi.org/10.2450/2013.010s.
Loomans JI, Kruip M, Carcao M, Jackson S, van Velzen AS, Peters M, et al. Desmopressin in moderate hemophilia A patients: a treatment worth considering. Haematologica. 2018;103(3):550–7. https://doi.org/10.3324/haematol.2017.180059.
Graf L. Extended half-life factor VIII and factor IX preparations. Transfus Med Hemother. 2018;45(2):86–91. https://doi.org/10.1159/000488060.
Shapiro AD, Ragni MV, Valentino LA, Key NS, Josephson NC, Powell JS, et al. Recombinant factor IX-Fc fusion protein (rFIXFc) demonstrates safety and prolonged activity in a phase 1/2a study in hemophilia B patients. Blood. 2012;119(3):666–72. https://doi.org/10.1182/blood-2011-07-367003.
Powell JS, Josephson NC, Quon D, Ragni MV, Cheng G, Li E, et al. Safety and prolonged activity of recombinant factor VIII Fc fusion protein in hemophilia A patients. Blood. 2012;119(13):3031–7. https://doi.org/10.1182/blood-2011-09-382846.
Santagostino E, Martinowitz U, Lissitchkov T, Pan-Petesch B, Hanabusa H, Oldenburg J, et al. Long-acting recombinant coagulation factor IX albumin fusion protein (rIX-FP) in hemophilia B: results of a phase 3 trial. Blood. 2016;127(14):1761–9. https://doi.org/10.1182/blood-2015-09-669234.
Oldenburg J, Carcao M, Lentz SR, Mahlangu J, Mancuso ME, Matsushita T, et al. Once-weekly prophylaxis with 40 IU/kg nonacog beta pegol (N9-GP) achieves trough levels of >15% in patients with haemophilia B: pooled data from the paradigm trials. Haemophilia. 2018;24(6):911–20. https://doi.org/10.1111/hae.13608.
Björkman S, Oh M, Spotts G, Schroth P, Fritsch S, Ewenstein BM, et al. Population pharmacokinetics of recombinant factor VIII: the relationships of pharmacokinetics to age and body weight. Blood. 2012;119(2):612–8. https://doi.org/10.1182/blood-2011-07-360594.
Björkman S, Ahlen V. Population pharmacokinetics of plasma-derived factor IX in adult patients with haemophilia B: implications for dosing in prophylaxis. Eur J Clin Pharmacol. 2012;68(6):969–77. https://doi.org/10.1007/s00228-012-1211-z.
Mould DR, Upton RN. Basic concepts in population modeling, simulation, and model-based drug development. CPT Pharmacometrics Syst Pharmacol. 2012;1:e6. https://doi.org/10.1038/psp.2012.4.
Dargaud Y, Delavenne X, Hart DP, Meunier S, Mismetti P. Individualized PK-based prophylaxis in severe haemophilia. Haemophilia. 2018;24(Suppl. 2):3–17. https://doi.org/10.1111/hae.13397.
Bonate PL. A brief introduction to Monte Carlo simulation. Clin Pharmacokinet. 2001;40(1):15–22. https://doi.org/10.2165/00003088-200140010-00002.
Preijers T, Hazendonk H, Fijnvandraat K, Leebeek FWG, Cnossen MH, Mathot RAA. In silico evaluation of limited blood sampling strategies for individualized recombinant factor IX prophylaxis in hemophilia B patients. J Thromb Haemost. 2017;15(9):1737–46. https://doi.org/10.1111/jth.13771.
Brekkan A, Degerman J, Jonsson S. Model-based evaluation of low-dose factor VIII prophylaxis in haemophilia A. Haemophilia. 2019;25(3):408–15. https://doi.org/10.1111/hae.13753.
Ette EI, Williams PJ. Population pharmacokinetics II: estimation methods. Ann Pharmacother. 2004;38(11):1907–15. https://doi.org/10.1345/aph.1E259.
Carter AA, Rosenbaum SE, Dudley MN. Review of methods in population pharmacokinetics. Clin Res Regul Aff. 2008;12(1):1–21. https://doi.org/10.3109/10601339509079574.
Proost JH, Schiere S, Eleveld DJ, Wierda JM. Simultaneous versus sequential pharmacokinetic-pharmacodynamic population analysis using an iterative two-stage Bayesian technique. Biopharm Drug Dispos. 2007;28(8):455–73. https://doi.org/10.1002/bdd.575.
Sun H, Fadiran EO, Jones CD, Lesko L, Huang SM, Higgins K, et al. Population pharmacokinetics: a regulatory perspective. Clin Pharmacokinet. 1999;37(1):41–58. https://doi.org/10.2165/00003088-199937010-00003.
Steimer JL, Mallet A, Golmard JL, Boisvieux JF. Alternative approaches to estimation of population pharmacokinetic parameters: comparison with the nonlinear mixed-effect model. Drug Metab Rev. 1984;15(1–2):265–92. https://doi.org/10.3109/03602538409015066.
Ariano RE, Duke PC, Sitar DS. The influence of sparse data sampling on population pharmacokinetics: a post hoc analysis of a pharmacokinetic study of morphine in healthy volunteers. Clin Ther. 2012;34(3):668–76. https://doi.org/10.1016/j.clinthera.2012.01.023.
Sheiner LB. The population approach to pharmacokinetic data analysis: rationale and standard data analysis methods. Drug Metab Rev. 1984;15(1–2):153–71. https://doi.org/10.3109/03602538409015063.
Mould DR, Upton RN. Basic concepts in population modeling, simulation, and model-based drug development-part 2: introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst Pharmacol. 2013;2:e38. https://doi.org/10.1038/psp.2013.14.
Karlsson MO, Sheiner LB. The importance of modeling interoccasion variability in population pharmacokinetic analyses. J Pharmacokinet Biopharm. 1993;21(6):735–50. https://doi.org/10.1007/bf01113502.
Holford N, Heo YA, Anderson B. A pharmacokinetic standard for babies and adults. J Pharm Sci. 2013;102(9):2941–52. https://doi.org/10.1002/jps.23574.
Germovsek E, Barker CI, Sharland M, Standing JF. Scaling clearance in paediatric pharmacokinetics: all models are wrong, which are useful? Br J Clin Pharmacol. 2017;83(4):777–90. https://doi.org/10.1111/bcp.13160.
Holford NH. A size standard for pharmacokinetics. Clin Pharmacokinet. 1996;30(5):329–32. https://doi.org/10.2165/00003088-199630050-00001.
Anderson BJ, Holford NH. Mechanism-based concepts of size and maturity in pharmacokinetics. Annu Rev Pharmacol Toxicol. 2008;48:303–32. https://doi.org/10.1146/annurev.pharmtox.48.113006.094708.
Standing JF. Understanding and applying pharmacometric modelling and simulation in clinical practice and research. Br J Clin Pharmacol. 2017;83(2):247–54. https://doi.org/10.1111/bcp.13119.
Ette EI, Williams PJ, Lane JR. Population pharmacokinetics III: design, analysis, and application of population pharmacokinetic Studies. Ann Pharmacother. 2004;38(12):2136–44. https://doi.org/10.1345/aph.1E260.
Stass H. Determination of minimal sampling time points for reliable pharmacokinetic evaluation of recombinant factor VIII ? An exploratory population pharmacokinetic analysis in paediatric patients suffering from severe haemophilia. Haemophilia. 2006;12(s4):50–5. https://doi.org/10.1111/j.1365-2516.2006.01334.x.
Longo G, Messori A, Morfini M, Baudo F, Ciavarella N, Cinotti S, et al. Evaluation of factor VIII pharmacokinetics in hemophilia-A subjects undergoing surgery and description of a nomogram for dosing calculations. Am J Hematol. 1989;30(3):140–9. https://doi.org/10.1002/ajh.2830300305.
Ruffo S, Messori A, Longo G, Matucci M, Morfini M, Rossi-Ferrini P. A microcomputer program for individualizing factor VIII dosage in hemophilia patients undergoing major surgery. Comp Methods Prog Biomed. 1986;23(1):37–46. https://doi.org/10.1016/0169-2607(86)90078-7.
Ruffo S, Messori A, Grasela TH, Longo G, Donati-Cori G, Matucci M, et al. A calculator program for clinical application of the Bayesian method of predicting plasma drug levels. Comp Prog Biomed. 1985;19(2–3):167–77. https://doi.org/10.1016/0010-468x(85)90008-x.
Messori A, Longo G, Morfini M, Cinotti S, Filimberti E, Giustarini G, et al. Multi-variate analysis of factors governing the pharmacokinetics of exogenous factor VIII in haemophiliacs. Eur J Clin Pharmacol. 1988;35(6):663–8. https://doi.org/10.1007/bf00637604.
Sheiner LB, Beal SL. Evaluation of methods for estimating population pharmacokinetics parameters. I. Michaelis-Menten model: routine clinical pharmacokinetic data. J Pharmacokinet Biopharm. 1980;8(6):553–71. https://doi.org/10.1007/bf01060053.
Bauer RJ. NONMEM tutorial part II: estimation methods and advanced examples. CPT Pharmacometrics Syst Pharmacol. 2019. https://doi.org/10.1002/psp4.12422.
Samson A, Lavielle M, Mentre F. The SAEM algorithm for group comparison tests in longitudinal data analysis based on non-linear mixed-effects model. Stat Med. 2007;26(27):4860–75. https://doi.org/10.1002/sim.2950.
Sukarnjanaset W, Wattanavijitkul T, Jarurattanasirikul S. Evaluation of FOCEI and SAEM estimation methods in population pharmacokinetic analysis using NONMEM® across rich, medium, and sparse sampling data. Eur J Drug Metab Pharmacokinet. 2018;43(6):729–36. https://doi.org/10.1007/s13318-018-0484-8.
Karafoulidou A, Suarez E, Anastasopoulou I, Katsarou O, Kouramba A, Kotsi P, et al. Population pharmacokinetics of recombinant factor VIII: C (ReFacto) in adult HIV-negative and HIV-positive haemophilia patients. Eur J Clin Pharmacol. 2009;65(11):1121–30. https://doi.org/10.1007/s00228-009-0699-3.
Björkman S, Berntorp E. Pharmacokinetics of coagulation factors: clinical relevance for patients with haemophilia. Clin Pharmacokinet. 2001;40(11):815–32. https://doi.org/10.2165/00003088-200140110-00003.
Delavenne X, Dargaud Y, Ollier E, Negrier C. Dose tailoring of human cell line-derived recombinant factor VIII simoctocog alfa: using a limited sampling strategy in patients with severe haemophilia A. Br J Clin Pharmacol. 2019;85(4):771–81. https://doi.org/10.1111/bcp.13858.
Björkman S, Folkesson A, Jonsson S. Pharmacokinetics and dose requirements of factor VIII over the age range 3–74 years: a population analysis based on 50 patients with long-term prophylactic treatment for haemophilia A. Eur J Clin Pharmacol. 2009;65(10):989–98. https://doi.org/10.1007/s00228-009-0676-x.
Abrantes JA, Nielsen EI, Korth-Bradley J, Harnisch L, Jonsson S. Elucidation of factor VIII activity pharmacokinetics: a pooled population analysis in patients with hemophilia A treated with moroctocog alfa. Clin Pharmacol Ther. 2017;102(6):977–88. https://doi.org/10.1002/cpt.716.
Jimenez-Yuste V, Lejniece S, Klamroth R, Suzuki T, Santagostino E, Karim FA, et al. The pharmacokinetics of a B-domain truncated recombinant factor VIII, turoctocog alfa (NovoEight®), in patients with hemophilia A. J Thromb Haemost. 2015;13(3):370–9. https://doi.org/10.1111/jth.12816.
Mahlangu J, Young G, Hermans C, Blanchette V, Berntorp E, Santagostino E. Defining extended half-life rFVIII-A critical review of the evidence. Haemophilia. 2018;24(3):348–58. https://doi.org/10.1111/hae.13438.
Nestorov I, Neelakantan S, Ludden TM, Li S, Jiang H, Rogge M. Population pharmacokinetics of recombinant factor VIII Fc fusion protein. Clin Pharmacol Drug Develop. 2015;4(3):163–74. https://doi.org/10.1002/cpdd.167.
Shah A, Solms A, Wiegmann S, Ahsman M, Berntorp E, Tiede A, et al. Direct comparison of two extended-half-life recombinant FVIII products: a randomized, crossover pharmacokinetic study in patients with severe hemophilia A. Ann Hematol. 2019;98(9):2035–44. https://doi.org/10.1007/s00277-019-03747-2.
Chelle P, Yeung CHT, Croteau SE, Lissick J, Balasa V, Ashburner C, et al. Development and validation of a population-pharmacokinetic model for rurioctacog alfa pegol (Adynovate®): a report on behalf of the WAPPS-Hemo Investigators Ad Hoc Subgroup. Clin Pharmacokinet. 2020;59(2):245–56. https://doi.org/10.1007/s40262-019-00809-6.
Kepa S, Horvath B, Reitter-Pfoertner S, Schemper M, Quehenberger P, Grundbichler M, et al. Parameters influencing FVIII pharmacokinetics in patients with severe and moderate haemophilia A. Haemophilia. 2015;21(3):343–50. https://doi.org/10.1111/hae.12592.
Potgieter JJ, Damgaard M, Hillarp A. One-stage vs. chromogenic assays in haemophilia A. Eur J Haematol. 2015;94(Suppl. 77):38–44. https://doi.org/10.1111/ejh.12500.
Hazendonk H, Fijnvandraat K, Lock J, Driessens M, van der Meer F, Meijer K, et al. A population pharmacokinetic model for perioperative dosing of factor VIII in hemophilia A patients. Haematologica. 2016;101(10):1159–69. https://doi.org/10.3324/haematol.2015.136275.
Hazendonk HC, Lock J, Mathot RA, Meijer K, Peters M, Laros-van Gorkom BA, et al. Perioperative treatment of hemophilia A patients: blood group O patients are at risk of bleeding complications. J Thromb Haemost. 2016;14(3):468–78. https://doi.org/10.1111/jth.13242.
Schutte LM, van Hest RM, Stoof SCM, Leebeek FWG, Cnossen MH, Kruip M, et al. Pharmacokinetic modelling to predict FVIII: C response to desmopressin and its reproducibility in nonsevere haemophilia A patients. Thromb Haemost. 2018;118(4):621–9. https://doi.org/10.1160/TH17-06-0390.
Feng D, Stafford KA, Broze GJ, Stafford DW. Evidence of clinically significant extravascular stores of factor IX. J Thromb Haemost. 2013;11(12):2176–8. https://doi.org/10.1111/jth.12421.
Björkman S. Population pharmacokinetics of recombinant factor IX: implications for dose tailoring. Haemophilia. 2013;19(5):753–7. https://doi.org/10.1111/hae.12188.
Brekkan A, Berntorp E, Jensen K, Nielsen EI, Jonsson S. Population pharmacokinetics of plasma-derived factor IX: procedures for dose individualization. J Thromb Haemost. 2016;14(4):724–32. https://doi.org/10.1111/jth.13271.
Suzuki A, Tomono Y, Korth-Bradley JM. Population pharmacokinetic modelling of factor IX activity after administration of recombinant factor IX in patients with haemophilia B. Haemophilia. 2016;22(5):e359–e366366. https://doi.org/10.1111/hae.12969.
Björkman S. Pharmacokinetics of plasma-derived and recombinant factor IX: implications for prophylaxis and on-demand therapy. Haemophilia. 2013;19(6):808–13. https://doi.org/10.1111/hae.12216.
Franchini M, Frattini F, Crestani S, Sissa C, Bonfanti C. Treatment of hemophilia B: focus on recombinant factor IX. Biologics. 2013;7:33–8. https://doi.org/10.2147/BTT.S31582.
Zhang Y, Roberts J, Bensen-Kennedy D, Jacobs I, Santagostino E, Voigt C, et al. Population pharmacokinetics of a new long-acting recombinant coagulation factor IX albumin fusion protein for patients with severe hemophilia B. J Thromb Haemost. 2016;14(11):2132–40. https://doi.org/10.1111/jth.13444.
Collins PW, Moss J, Knobe K, Groth A, Colberg T, Watson E. Population pharmacokinetic modeling for dose setting of nonacog beta pegol (N9-GP), a glycoPEGylated recombinant factor IX. J Thromb Haemost. 2012;10(11):2305–12. https://doi.org/10.1111/jth.12000.
Diao L, Li S, Ludden T, Gobburu J, Nestorov I, Jiang H. Population pharmacokinetic modelling of recombinant factor IX Fc fusion protein (rFIXFc) in patients with haemophilia B. Clin Pharmacokinet. 2014;53(5):467–77. https://doi.org/10.1007/s40262-013-0129-7.
Preijers T, Hazendonk H, Liesner R, Chowdary P, Driessens MHE, Hart D, et al. Population pharmacokinetics of factor IX in hemophilia B patients undergoing surgery. J Thromb Haemost. 2018;16(11):2196–207. https://doi.org/10.1111/jth.14292.
Abrantes JA, Jonsson S, Karlsson MO, Nielsen EI. Handling interoccasion variability in model-based dose individualization using therapeutic drug monitoring data. Br J Clin Pharmacol. 2019;85(6):1326–36. https://doi.org/10.1111/bcp.13901.
Martinowitz U, Schulman S, Gitel S, Horozowski H, Heim M, Varon D. Adjusted dose continuous infusion of factor VIII in patients with haemophilia A. Br J Haematol. 1992;82(4):729–34. https://doi.org/10.1111/j.1365-2141.1992.tb06951.x.
Schulman S, Wallensten R, White B, Smith OP. Efficacy of a high purity, chemically treated and nanofiltered factor IX concentrate for continuous infusion in haemophilia patients undergoing surgery. Haemophilia. 1999;5(2):96–100. https://doi.org/10.1046/j.1365-2516.1999.00284.x.
Batorova A, Martinowitz U. Intermittent injections vs. continuous infusion of factor VIII in haemophilia patients undergoing major surgery. Br J Haematol. 2000;110(3):715–20. https://doi.org/10.1046/j.1365-2141.2000.02226.x.
Hazendonk HC, van Moort I, Fijnvandraat K, Kruip MJ, Laros-van Gorkom BA, van der Meer FJ, et al. The "OPTI-CLOT" trial: a randomised controlled trial on periOperative PharmacokineTIc-guided dosing of CLOTting factor concentrate in haemophilia A. Thromb Haemost. 2015;114(3):639–44. https://doi.org/10.1160/TH14-11-0925.
Anderson BJ, Holford NH. Mechanistic basis of using body size and maturation to predict clearance in humans. Drug Metab Pharmacokinet. 2009;24(1):25–36. https://doi.org/10.2133/dmpk.24.25.
Sinha J, Al-Sallami HS, Duffull SB. Choosing the allometric exponent in covariate model building. Clin Pharmacokinet. 2019;58(1):89–100. https://doi.org/10.1007/s40262-018-0667-0.
Bauer A, Wolfsegger MJ. Adjustment of endogenous concentrations in pharmacokinetic modeling. Eur J Clin Pharmacol. 2014;70(12):1465–70. https://doi.org/10.1007/s00228-014-1759-x.
Preijers T, van Moort I, Fijnvandraat K, Leebeek FWG, Cnossen MH, Mathot RAA, et al. Cross-evaluation of pharmacokinetic-guided dosing tools for factor VIII. Thromb Haemost. 2018;118(3):514–25. https://doi.org/10.1055/s-0038-1623531.
Preijers T, Schutte LM, Kruip M, Cnossen MH, Leebeek FWG, van Hest RM, et al. Strategies for individualized dosing of clotting factor concentrates and desmopressin in hemophilia A and B. Ther Drug Monitor. 2019. https://doi.org/10.1097/FTD.0000000000000625.
Hajducek DM, Chelle P, Hermans C, Iorio A, McEneny-King A, Yu J, et al. Development and evaluation of the population pharmacokinetic models for FVIII and FIX concentrates of the WAPPS-Hemo project. Haemophilia. 2020. https://doi.org/10.1111/hae.13977.
Schutte LM, Cnossen MH, van Hest RM, Driessens MHE, Fijnvandraat K, Polinder S, et al. Desmopressin treatment combined with clotting factor VIII concentrates in patients with non-severe haemophilia A: protocol for a multicentre single-armed trial, the DAVID study. BMJ Open. 2019;9(4):e022719. https://doi.org/10.1136/bmjopen-2018-022719.
Bolon-Larger M, Chamouard V, Bressolle F, Boulieu R. A limited sampling strategy for estimating individual pharmacokinetic parameters of coagulation factor VIII in patients with hemophilia A. Ther Drug Monitor. 2007;29(1):20–6. https://doi.org/10.1097/FTD.0b013e3180311384.
Garmann D, McLeay S, Shah A, Vis P, Maas Enriquez M, Ploeger BA. Population pharmacokinetic characterization of BAY 81–8973, a full-length recombinant factor VIII: lessons learned: importance of including samples with factor VIII levels below the quantitation limit. Haemophilia. 2017;23(4):528–37. https://doi.org/10.1111/hae.13192.
Zhang Y, Roberts J, Tortorici M, Veldman A, St Ledger K, Feussner A, et al. Population pharmacokinetics of recombinant coagulation factor VIII-SingleChain in patients with severe hemophilia A. J Thromb Haemost. 2017;15(6):1106–14. https://doi.org/10.1111/jth.13662.
Shah A, Solms A, Garmann D, Katterle Y, Avramova V, Simeonov S, et al. Improved pharmacokinetics with BAY 81–8973 versus antihemophilic factor (recombinant) plasma/albumin-free method: a randomized pharmacokinetic study in patients with severe hemophilia A. Clin Pharmacokinet. 2017;56(9):1045–55. https://doi.org/10.1007/s40262-016-0492-2.
Abrantes JA, Solms A, Garmann D, Nielsen EI, Jonsson S, Karlsson MO. Relationship between factor VIII activity, bleeds and individual characteristics in severe hemophilia A patients. Haematologica. 2019. https://doi.org/10.3324/haematol.2019.217133.
Chelle P, Yeung CHT, Bonanad S, Morales Munoz JC, Ozelo MC, Megias Vericat JE, et al. Routine clinical care data for population pharmacokinetic modeling: the case for Fanhdi/Alphanate in hemophilia A patients. J Pharmacokinet Pharmacodyn. 2019;46(5):427–38. https://doi.org/10.1007/s10928-019-09637-4.
McEneny-King A, Chelle P, Foster G, Keepanasseril A, Iorio A, Edginton AN. Development and evaluation of a generic population pharmacokinetic model for standard half-life factor VIII for use in dose individualization. J Pharmacokinet Pharmacodyn. 2019;46(5):411–26. https://doi.org/10.1007/s10928-019-09634-7.
Allard Q, Djerada Z, Pouplard C, Repesse Y, Desprez D, Galinat H, et al. Real life population pharmacokinetics modelling of eight factors VIII in patients with severe haemophilia A: is it always relevant to switch to an extended half-life? Pharmaceutics. 2020. https://doi.org/10.3390/pharmaceutics12040380.
Tiede A, Abdul Karim F, Jimenez-Yuste V, Klamroth R, Lejniece S, Suzuki T, et al. Factor VIII activity and bleeding risk during prophylaxis for severe hemophilia A: a population pharmacokinetic model. Haematologica. 2020. https://doi.org/10.3324/haematol.2019.241554.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
No sources of funding were used to assist with the preparation of this review.
Conflict of interest
TP, LS, and RH have no conflicts of interest that are directly relevant to the content of this review. RM has received grants from governmental and societal research institutes such as NWO, ZonMW, and Innovation Fund and unrestricted investigator research grants from Baxter/Baxalta/Shire/Takeda, Bayer, CSL Behring, and Sobi. He has served as an advisor for Bayer, CSL Behring, Merck Sharp & Dohme, and Baxter/Baxalta/Shire/Takeda. All grants and fees were paid to the institution. MC has received grants from governmental research institutes such as Dutch Research Institute (NWO), ZonMW, Innovation Fund, and NWO-NWA and unrestricted investigator-initiated research grants as well as educational and travel funding from the following companies over the years: Pfizer, Baxter/Baxalta/Shire, Bayer Schering Pharma, CSL Behring, Sobi Biogen, Novo Nordisk, Novartis, and Nordic Pharma, and has served as a member on steering boards of Roche and Bayer. All grants, awards, and fees received went to the institution. FWGL received unrestricted search grants of CS: Behring, Takeda, and UniQure. He is also a consultant for CSL Behring, Takeda, and UniQure of which fees go to the institution. He received travel support from Sobi. He is a DSMB member for a study conducted by Roche. MK reports grants from Daiichi Sankyo, Boehringer Ingelheim, Pfizer, and Sobi, and grants and fees from Bayer, all outside the submitted work and payments to the Department of Hematology of Erasmus MC.
Availability of Data and Material
Not applicable.
Code Availability
Not applicable.
Author contributions
TP and LS performed the literature search, analyzed the data, and wrote the manuscript. RH and RM supervised the study and provided critical guidance during the analysis. MC, FL, and MK critically reviewed the paper and provided additional comments. All authors approved the final version of the manuscript.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Preijers, T., Schütte, L.M., Kruip, M.J.H.A. et al. Population Pharmacokinetics of Clotting Factor Concentrates and Desmopressin in Hemophilia. Clin Pharmacokinet 60, 1–16 (2021). https://doi.org/10.1007/s40262-020-00936-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-020-00936-5