FormalPara Key Points

Brigatinib pharmacokinetic data from 442 adults (105 healthy volunteers and 337 patients with cancer) enrolled across five studies were adequately described by a three-compartment model with transit compartment input.

Albumin was included as a covariate on apparent clearance in the final population pharmacokinetic model, explaining approximately 5% of variability in apparent clearance.

Sex, age (18–83 years), race, body weight (40.6–172.0 kg), mild or moderate renal impairment (estimated glomerular filtration rate ≥ 32.7 mL/min/1.73 m2), total bilirubin (1–74 μmol/L), aspartate aminotransferase (10–99 U/L), and alanine aminotransferase (5–129 U/L) were not found to impact brigatinib exposure.

1 Introduction

Brigatinib is an inhibitor of oncogenic variants of the anaplastic lymphoma kinase gene, ALK, including the ALK fusions (e.g., EML4-ALK) that are found in non-small cell lung cancer (NSCLC) [1,2,3]. An accelerated approval of brigatinib was granted in the USA in 2017, followed by approval in the European Union and Canada in 2018, based on efficacy and safety results from a randomized, multicenter phase II trial (ALK in Lung Cancer Trial of AP26113 [ALTA], NCT02094573) in adult patients with locally advanced or metastatic ALK-positive NSCLC who had progressed on crizotinib [4]. In ALTA, the recommended dosing regimen of brigatinib (180 mg once daily [qd] with a 7-day lead-in at 90 mg qd) demonstrated high systemic and central nervous system response rates and median progression-free survival of 16.7 months in crizotinib-refractory patients [5, 6]. The step-up brigatinib dosing regimen (180 mg qd with a 7-day lead-in at 90 mg qd) was selected because starting treatment at the lower initial dose (90 mg) mitigated the risk of moderate-to-severe pulmonary adverse events that have been observed in a small subset of patients within the first 7 days after initiation of higher doses of brigatinib, while maintaining the efficacy associated with the 180-mg dose [3, 4, 7, 8]. A phase III trial (ALTA-1L) is comparing the safety and efficacy of brigatinib vs crizotinib in patients with ALK + NSCLC who are ALK inhibitor naive [8]. At the first prespecified interim analysis of ALTA-1L, the primary endpoint was met, demonstrating superior progression-free survival assessed by a blinded independent review committee in the brigatinib arm compared with the crizotinib arm (hazard ratio, 0.49; p < 0.001; 12-month event-free rate, 67%, brigatinib; 43%, crizotinib) [8].

Brigatinib has high solubility and permeability and is orally bioavailable. It is approximately 90% bound to human plasma proteins [2, 9, 10]. The mean plasma elimination half-life is 25 h [9]. Following oral administration of a single 180-mg dose of radiolabeled brigatinib to healthy volunteers, approximately 65% and 25% of the administered dose was recovered in feces (unchanged brigatinib, 41%) and urine (unchanged brigatinib, 86%), respectively [9]. Approximately 50% of the overall radiolabeled dose was recovered as unchanged drug with the remainder metabolized to a number of inactive or minor metabolites, primarily by cytochrome P450 (CYP) 3A and CYP2C8 [9]. As a renal pathway was not expected to be a major route of clearance for brigatinib, the clinical development program included patients with mild or moderate renal impairment, whereas the effects of severe renal impairment on brigatinib pharmacokinetics were evaluated in a dedicated renal impairment study. Results of this dedicated study in patients with severe renal impairment supported the recommendation of a 50% reduction in the brigatinib dose for these patients as an approximately twofold increase in unbound area under the concentration vs time curve (AUC) from time 0 to infinity (AUC0–∞) was observed in patients with severe renal impairment as compared with patients with normal renal function [9]. Results of a dedicated hepatic impairment study supported the recommendation of no dosage adjustment for patients with mild-to-moderate hepatic impairment (Child–Pugh A and B) and a 40% dose reduction for patients with severe hepatic impairment (Child–Pugh C) owing to an approximately 37% increase in unbound brigatinib systemic exposure (AUC0–∞) in these patients [9]. A food-effect study reported a relatively small decrease of 13% in maximum plasma concentration following a high-fat meal without a corresponding decrease in AUC, thereby supporting the recommendation that brigatinib tablets may be administered without regard to food intake [10].

The objectives of the present analysis were to develop a population pharmacokinetic (PK) model for brigatinib based on available data from relevant phase I/II trials, including the identification and quantification of sources of variability (e.g., age, weight, sex, race, and renal and hepatic function) in brigatinib PK parameters and to determine if dose adjustments are required in patients with ALK-positive NSCLC based on these patient-specific factors.

2 Methods

2.1 Data Collection

Plasma concentrations of brigatinib over time were obtained from three phase I studies conducted in healthy volunteers [10, 11], one phase I/II study conducted in patients with advanced malignancies [3], and one phase II trial in patients with ALK-positive NSCLC, who had progressed on crizotinib [4] (Table 1). The trials in healthy volunteers tested single doses of 90 mg, 120 mg, and 180 mg [11]. One of the phase I trials was a food effect study in which healthy volunteers received brigatinib 180 mg under fasting conditions or after completion of a high-fat meal [10]; only PK data obtained under fasting conditions were included in the population PK analysis. Another of the phase I trials evaluated the effects of rifampin, itraconazole, and gemfibrozil on the pharmacokinetics of brigatinib in healthy volunteers [11]; only data obtained after a single dose of 90 mg or 180 mg of brigatinib (without concomitant administration of rifampin, itraconazole, or gemfibrozil) were included in the population PK analysis. The phase I/II trial in patients with cancer investigated dose regimens ranging from 30 to 300 mg qd and from 60 to 120 mg twice daily [3], and the phase II trial in patients with ALK-positive NSCLC evaluated doses of 90 mg qd and 180 mg qd with a 7-day lead-in at 90 mg qd [4]. The blood sampling schedule for each trial is shown in Table 1. All five trials were performed in accordance with International Council for Harmonisation Good Clinical Practice Guidelines.

Table 1 Studies included in the population pharmacokinetic (PK) analysis
Full size table

Two validated liquid chromatographic/mass spectroscopic methods were used to analyze brigatinib PK samples during clinical development. The first method was used initially to analyze all samples in the phase I/II patient trial. This assay had a lower limit of quantitation (LLOQ) and an upper limit of quantitation of 0.100 ng/mL and 500 ng/mL, respectively, for brigatinib. This method had an intra-run precision for brigatinib in human plasma samples for the high- and low-range assays that ranged from 3.3 to 10.0% and 1.1 to 12.7% coefficient of variation (CV), respectively, with bias of − 15.8 to 0.3% and − 8.7 to − 2.3%. Inter-run precision ranged from 4.8 to 8.8% and 3.1 to 8.4% CV, with a bias of − 6.3 to − 1.3% and − 7.3 to − 4.2% [10]. A second method was subsequently developed to quantify brigatinib plasma concentrations higher than 500 ng/mL. This was the principal method used to analyze all plasma samples in the first phase I study in healthy volunteers (AP26113-13-102), the phase I food-effect study (AP26113-13-103), the phase I drug–drug interaction study (AP26113-15-105) [11], and the phase II trial (ALTA) [4]. This single-range assay had an LLOQ and upper limit of quantitation for brigatinib of 25 ng/mL and 2500 ng/mL, respectively, and intra-run precision for brigatinib in human plasma that ranged from 1.0 to 12.9% CV, with a bias of − 11.6 to 5.6%, as well as inter-run precision that ranged from 1.7 to 10.1% CV, with a bias of − 2.5 to 1.1% [10]. Samples quantified as having brigatinib concentrations below the LLOQ of the second method (< 25 ng/mL) were reanalyzed using the first method. Therefore, the effective analytical range employed in the studies included in this population PK analysis ranged from 0.1 to 2500 ng/mL.

2.2 Population Pharmacokinetic Modeling

The population PK analyses were performed using NONMEM (version 7.3; ICON Development Solutions, Hanover, MD, USA [12]). Graphical and descriptive summaries were produced using R [13] version 3.4.4. Data from all five studies were fit simultaneously using the NONMEM first-order conditional estimation algorithm. Because of a low number of samples (< 5%) below the LLOQ of the assays (i.e., < 0.1 ng/mL), no method of imputation nor censoring was warranted for the analysis. Based on exploratory analyses, two- and three-compartment models with linear elimination with varying parameterization for brigatinib absorption were evaluated for model discrimination. Absorption models tested included first-order input with and without a lag time; dual, parallel first-order processes, each with a unique lag-time; zero-order absorption; mixed first- and zero-order absorption; and, finally, the transit absorption proposed by Savic et al. [14].

Each model included a variance component characterizing inter-individual variability in model parameters that was implemented with the following form:

$$ \theta_{i,n} = \left( {\theta_{{{\text{TV}},n}} e^{{\eta_{i,n} }} } \right) $$
(1)
$$ \left( {\eta_{1, \ldots ,} \eta_{p} } \right) = {\text{MVN}}\left( {0, \varOmega } \right), $$
(2)

where \( \theta_{i,n} \) is the value of the nth PK parameter of the ith individual, \( \theta_{{{\text{TV}},n}} \)is the typical value of the nth PK parameter in the population, and \( n_{i,n} \) is the random inter-individual deviation from the typical value \( \theta_{{{\text{TV}},n}} \)for participant \( i \). Inter-individual random effects \( \left( {\eta_{1, \ldots ,} \eta_{p} } \right) \) are multivariate normally distributed values with mean 0 and estimated variance \( \omega_{n}^{2} \) included in the variance-covariance (Ω) matrix. Residual unexplained variability was evaluated using additive, proportional, and mixed (additive and proportional) models.

2.3 Covariate Model Development

A predetermined list of covariates was tested for effects on PK parameters of apparent clearance (CL/F) and apparent central volume of distribution (V1/F) in two steps. Covariates tested for effects on brigatinib clearance included categorical covariates of sex (male vs female), patient status (cancer patient vs healthy volunteer), and race (white, black, Asian, or other) and continuous covariates of age at study entry, body weight, body surface area, total bilirubin, aspartate aminotransferase (AST), alanine aminotransferase (ALT), albumin, and estimated glomerular filtration rate (eGFR). Covariates tested for effects on the volume of distribution included categorical covariates of sex, patient status, and race and continuous covariates of body weight, body surface area, and albumin. Patient status did not differentiate between patients with NSCLC and other types of ALK + cancer because no differences in pharmacokinetics between these groups were identified in the phase I study. First, a univariate analysis was performed to assess whether a particular covariate resulted in a significant reduction in the minimum value of the objective function (p < 0.01) and resulted in at least a 5% reduction in inter-individual variability for a given parameter [15]. Covariate models meeting both criteria were then evaluated in a stepwise procedure where a covariate was retained in the model, if the reduction in the minimum value of the objective function was ≥ 6.63 (p < 0.01 for one degree of freedom) in the forward inclusion step, and ≥ 10.83 (p < 0.001 for one degree of freedom) in the backward exclusion step [16].

Continuous covariates were tested in the model using power functions with the following form:

$$ \theta_{i} = \theta_{\text{TV}} \cdot \left( {\frac{{{\text{Cov}}_{i} }}{{{\text{Cov}}_{\text{reference value}} }}} \right)^{{\theta_{\text{eff}} }} , $$
(3)

where \( \theta_{i} \) is the population value of PK parameters for participants with covariates equal to \( {\text{Cov}}_{i} \), \( \theta_{\text{TV}} \) is the typical value of the parameter for participants having the covariate equal to the reference value (\( {\text{Cov}}_{\text{reference value}} \)), and \( \theta_{\text{eff}} \) is a parameter characterizing the effect of the covariate on parameter \( \theta \). Reference values were based on the population PK dataset.

Categorical covariates with numerical values from \( 1 \) to \( n \) were tested in the model using an exponential function:

$$ \theta_{i} = \theta_{\text{TV}} \cdot \exp \left( {\mathop \sum \limits_{i = 2}^{n} \theta_{{{\text{effi}},i}} \cdot \left[ {{\text{Cov}} = i} \right]} \right), $$
(4)

where \( \theta_{\text{TV}} \) is the population value of PK parameters for participants in the first (or reference) category and \( { \exp }\left( {\theta_{\text{effi,i}} } \right) \) is the multiplicative effect of the category \( i \) on parameter \( \theta \).

2.4 Model Evaluation and Qualification

Base and covariate models were selected based on the decrease in the minimum objective function value, precision and accuracy of parameter estimation, successful model convergence, and by examining pertinent graphical representations of goodness of fit [17,18,19]. The performance of the final population PK model was also evaluated by a prediction-corrected visual predictive check, where the model was simulated with 1000 replicates and the 95% prediction interval of the 2.5th, 50th, and 97.5th percentiles of predicted (corrected) concentrations were computed and compared with the 2.5th, 50th, and 97.5th percentiles of prediction-corrected observed data [20]. Model robustness and parameter estimates were evaluated by 1000 bootstrap replicates, with replacement.

The final population PK model was also used to simulate steady-state brigatinib AUC and trough concentration exposures in patients receiving the 180-mg once-daily regimen. The effects of covariates of interest (including categorical covariates of sex, race, patient status, and renal function [normal: eGFR ≥ 90 mL/min/1.73 m2; mild impairment: eGFR 60 to < 90 mL/min/1.73 m2; moderate impairment: eGFR 30 to < 60 mL/min/1.73 m2] and continuous covariates of body weight, age, total bilirubin, AST, and ALT) were evaluated by calculating predicted PK parameters for an individual following a brigatinib 180-mg dose at steady state using the individual estimated clearance values and each covariate as a predictor. Median (range) baseline albumin levels used in the simulated patient population were 36 (20–47) g/L based on data from the phase I/II study in patients with advanced malignancies [3]. Model uncertainty was also considered during the simulation by creating 1000 replicates each with a different set of PK parameters obtained by sampling from the variance-covariance matrix of the final population PK model. Simulated AUC and trough concentration data were summarized as geometric mean and 95% confidence intervals, which were based on 1000 sets of bootstrapped parameters.

3 Results

3.1 Dataset Summary

The dataset for the population PK analysis included 442 participants from five clinical studies (Table 1) [3, 4, 11]; 105 participants were healthy volunteers and 337 patients had some form of cancer, of which 201 had ALK-positive NSCLC. Demographics and baseline characteristics of participants included in the analysis dataset are presented in Table 2. Of the 6086 PK samples available, 247 (4.1%) were excluded from the population PK analysis because they were below the limit of quantitation, 80 (1.3%) were excluded because of suspected sampling time recording errors or sample storage issues, and 28 (0.5%) were excluded because the absolute value of their conditional weighted residuals was greater than 4.

Table 2 Demographics and baseline characteristics of participants in the population pharmacokinetic (PK) analysis dataset
Full size table

3.2 Population Pharmacokinetic Model Development

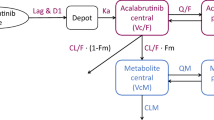
Based on exploratory and preliminary population PK analyses, two- and three-compartment models with linear elimination and varying parameterization for brigatinib absorption were selected for model discrimination. A three-compartment model with transit absorption resulted in the lowest objective function value (Fig. 1a). This model included random effects on CL/F, V1/F, the number of transit compartments, and mean transit time along with a proportional residual error model. A correlation (block variance) term between the random effects of CL/F and V1/F was found to improve model performance. Ultimately, including random effects on the second peripheral volume and fixing the number of transit compartments to an estimated value of 2.35 produced a model with the best fit.

Fig. 1
figure 1

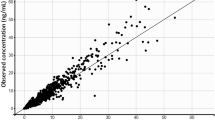
a Structural model describing the pharmacokinetics of brigatinib. b Prediction-corrected visual predictive check comparing model simulated values to the observed data for the overall population. Circles are observed brigatinib plasma concentrations, the solid red line represents the simulated median value, and red shaded areas represent the spread of the simulated median values (5th to 95th percentile). Blue lines represent the simulated 5th and 95th percentile and blue shaded areas represent the spread (5th to 95th percentile) of the simulated 5th and 95th percentile concentrations. Atr amount in the transit compartment, CL/F apparent extravascular clearance from the central compartment, IIV inter-individual variability, Ktr transit rate between transit compartments, Q1/F apparent intercompartmental distributional clearance between the central and first peripheral compartments, Q2/F apparent intercompartmental distributional clearance between the central and second peripheral compartments, V1/F apparent central compartment volume of distribution, V2/F apparent volume of the first peripheral compartment, V3/F apparent volume of the second peripheral compartment

Full size image

Univariate covariate analyses demonstrated that models with covariates of weight, sex, age, race, ALT, AST, total bilirubin, and eGFR did not reduce CL/F inter-individual variability by at least 5%. Only models with covariates of population (patients with cancer vs healthy volunteers) and albumin on CL/F resulted in at least a 5% reduction in CL/F inter-individual variability. Thus, only these two covariates were included in a stepwise analysis. The most significant covariate identified in the stepwise analysis was patient status (patients with cancer vs healthy volunteers). However, upon graphical examination (Electronic Supplementary Material [ESM] 1), patient status appeared to be correlated with serum albumin levels, such that patients with cancer had lower levels of albumin than healthy volunteers. As albumin may provide a more mechanistic explanation for the effect on brigatinib clearance, it was elected to retain the albumin effect on CL/F (a continuous covariate that is expected to be more statistically robust) in lieu of patient vs healthy volunteer status (a categorical variable). Further exploration of a model that included both albumin and patient vs healthy volunteer status did not result in a ≥ 5% change in CL/F inter-individual variability. Hence, the final model only had albumin as a covariate. Inclusion of albumin explained approximately 5% of the variability in CL/F, with patients at the 5th and 95th percentiles of albumin predicted to have approximately 22% lower and 20% higher CL/F, respectively, than a patient with the median albumin value.

3.3 Pharmacokinetic Model Assessment

Plots of observed brigatinib concentrations vs both population- and individual-predicted concentrations (ESM 2a), as well as plots of conditional weighted residuals vs time and predicted concentration (ESM 2b) indicated that the final model adequately described the observed data. The final model parameters, presented in Table 3, were estimated with good precision (CV < 20%) and with shrinkage values < 20% for clearance and volume parameters [18]. The CL/F in a typical individual (median) was estimated to be 10.6 L/h and, based on the inter-individual variability (48.4%), would be expected to vary from 4.8 to 24.0 L/h in 90% of the population. The V1/F was estimated at 207 L with inter-individual variability of 55.6%, implying that 90% of the population would have a volume of distribution between 83 and 520 L. A prediction-corrected visual predictive check indicated that the model was appropriately specified, as the model-predicted median and 95% confidence interval for each binned group of simulated concentrations largely encompassed the observed data (Fig. 1b; ESM 2c). Of 1000 bootstrap replicates, 87% achieved successful convergence and the final model parameters fell within the 95% confidence interval for the bootstrapped estimates (Table 3).

Table 3 Parameter estimates based on the final population pharmacokinetic (PK) model
Full size table

The effects of covariates of interest (including body weight, sex, age, race, mild or moderate renal impairment, total bilirubin, AST, and ALT) were evaluated by calculating predicted AUC for an individual following a brigatinib 180-mg dose at steady state using the individual estimated clearance values and each covariate as a predictor. Results of these simulations indicated that none of the covariates examined had clinically meaningful effects on brigatinib AUC (Figs. 2, 3). Post hoc stratification of predicted AUC (following 180 mg qd) by each covariate also confirmed that none of these covariates had a clinically meaningful effect on brigatinib systemic exposure (Fig. 4).

Fig. 2
figure 2

Correlations between individual-predicted brigatinib exposure (area under the concentration vs time curve [AUC]) and covariates of a age, b body weight, c alanine aminotransferase (ALT) levels, d aspartate aminotransferase (AST) levels, e total bilirubin, and f estimated glomerular filtration rate (eGFR) based on the final population pharmacokinetic model. Red and black dots represent the median and the 5th and 95th percentiles of the individual covariate values, respectively. Numbers (brackets) are the percent change (95% confidence interval) in the AUC relative to the values at the median, based on the linear regression (blue line) and corresponding 95% confidence interval (shaded region). The red line is the horizontal line passing through the AUC value corresponding to the median covariate value in the population. BILI bilirubin

Full size image
Fig. 3
figure 3

Individual-predicted brigatinib exposure (area under the concentration vs time curve [AUC]) by categorical covariates of a sex, b race, c estimated glomerular filtration rate category of impairment, and d patient status (patient with cancer vs healthy volunteer). Red and black dots represent the mean exposure in the reference category and remaining categories, respectively. Numbers (brackets) in the top of the plot are the percent change in AUC (95% confidence interval) relative to the median of the individual covariate values. Red lines represent the median value of the covariate across all groups. Numbers at the bottom of the lower boxplot hinge are the sample size in each category

Full size image
Fig. 4
figure 4

Predicted brigatinib exposure following 180-mg dose based on the final population pharmacokinetic model stratified by covariates of interest. The vertical dashed lines denote the median and 5th and 95th percentiles of predicted area under the concentration vs time curve (AUC) of brigatinib in a typical participant with baseline albumin level of 38 g/dL. For categorical covariates, the ratio of exposure for the category vs the reference category is shown. For continuous covariates, the ratio of exposure for the 95th and 5th percentiles of the covariate vs the medians is shown. The black shaded bar illustrates the 5th to 95th percentile exposure range across the entire population. The blue shaded bar represents the influence of baseline albumin on exposure. ALT alanine aminotransferase, AST aspartate aminotransferase, AUCSS area under the concentration vs time curve at steady state, CI confidence interval, eGFR estimated glomerular filtration rate. aCategories for eGFR: normal, ≥ 90 mL/min/1.73 m2; mild impairment, 60 to < 90 mL/min/1.73 m2; moderate impairment, 30 to < 60 mL/min/1.73 m2

Full size image

4 Discussion

Model-informed approaches drive patient-centric and efficient drug development and are vital to the success of accelerated oncology drug development programs [21,22,23]. The current population PK analyses based on data from five clinical studies showed that plasma concentrations of brigatinib following single and repeated doses in both healthy volunteers and patients with cancer were best described by a three-compartment model with a transit compartment for absorption. The effect of albumin level on CL/F was the only covariate included in the final model. Inclusion of albumin in the model explained approximately 5% of the variability in CL/F, indicating the lack of a clinically meaningful effect on brigatinib systemic exposure. The mechanistic reasons for the identified covariate effect of albumin on CL/F may be multifactorial. Decreasing albumin levels was associated with relatively minor decreases in total CL/F of brigatinib. If the effect of albumin was mainly related to an effect on plasma free fraction, an inverse relationship for total clearance would be expected. However, given the positive relationship that was estimated between albumin and total CL/F, the direction of this observed covariate effect suggests that the underlying mechanism is likely unrelated to a variation in plasma free fraction. One possible explanation is that decreased albumin may be indicative of advanced disease pathophysiology in patients with cancer, with associated pro-inflammatory status that may have resulted in suppression of CYP3A expression, leading to decreased CL/F of brigatinib. Importantly, irrespective of the underlying mechanism, the effect of albumin on CL/F (and thus AUC) can be considered minor and not of clinical relevance when viewed in relation to overall variability.

Covariates of body weight, sex, age, race, mild or moderate renal impairment, and mild hepatic impairment did not meaningfully explain variability in CL/F in the final population PK model, suggesting that no adjustment of the dose of brigatinib is required based on these covariates. Fixed dosing without correction for body size metrics is generally preferred for oral anticancer drugs because it simplifies dosing in clinical development and for patients and may also reduce the potential for dose calculation errors [24, 25].

Early demonstration of the lack of race effects on the PK profile of brigatinib in healthy Asian and white volunteers from an ethnobridging study (data on file), coupled with the current results of population PK modeling showing a lack of race effects, obviated the need for a phase I study in Japanese patients with cancer and enabled Asia-inclusive phase II/III trials [4, 8], which included study sites in Hong Kong, Singapore, South Korea, and Taiwan. Prospective consideration of potential PK differences in Asian patient populations can help to decrease access lag time in those populations and has become an important component of rationalized global clinical development strategies for investigational oncology drugs [26].

Patients with ALK-positive NSCLC who are prescribed brigatinib may have previously received cisplatin- or carboplatin-based regimens [27]. Therefore, these patients may exhibit varying levels of renal impairment due to nephrotoxicity associated with platinum-based chemotherapy [28, 29]. The results of the current population PK analysis suggested that dosage adjustments are not required for patients with mild or moderate renal impairment, thereby enabling a reduced renal impairment study design and model-informed prescribing guidance for patients with mild or moderate renal impairment [9, 30]. However, a dose reduction is recommended for patients with severe renal impairment based on the results of a dedicated trial in participants with severe renal impairment compared with participants with normal renal function [9, 30].

The final population PK model was also used to simulate steady-state brigatinib AUC in patients receiving 180 mg qd to permit a descriptive comparison of clinical exposures to target inhibition potencies. The distribution of these simulated brigatinib exposures were compared with in vitro estimates of IC50 and IC90 (concentrations of drug producing 50% and 90% inhibition, respectively) for inhibition of native EML4-ALK and mutants associated with resistance to ALK inhibitors (e.g., G1202R) (Fig. 5) [31]. In vitro IC50 and IC90 estimates were adjusted upward by a factor of two to account for the observed in vitro potency shift in the presence of plasma proteins (data on file, Takeda Pharmaceutical Company Limited). For the 180-mg qd dose, the 5th to 95th percentiles of the calculated Cav (average drug concentration; AUC/24) were 359–1606 ng/mL (614–2749 nM). In cellular assays, the IC90 (concentration of drug producing 90% inhibition) for brigatinib inhibition of native EML4-ALK was 38 nM, with mutant IC90 range of 22–762 nM [31]. After applying the twofold shift factor, the fifth percentile of Cav concentrations at 180 mg qd was 1.7-fold higher than the shifted IC50 of 368 nM for G1202R (an important mutant form of the target that is associated with treatment resistance to ALK inhibitors; Fig. 5) [31, 32]. Taken together, these analyses support the achievement of pharmacologically relevant exposures of brigatinib at clinically recommended doses consistent with the efficacy reported in ALTA.

Fig. 5
figure 5

Simulated brigatinib average drug concentration at steady state (Cav) at doses of 90 mg and 180 mg (black circles and lines) compared to the concentration of drug producing 50% inhibition (IC50) and concentration of drug producing 90% inhibition (IC90) for native EML4-ALK (blue lines) and the G1202R mutant (red lines). In vitro potency estimates were adjusted upward by a factor of two to account for the observed in vitro potency shift in the presence of plasma proteins

Full size image

5 Conclusions

Brigatinib pharmacokinetics in plasma following single and repeated doses in both healthy volunteers and patients with cancer was best described by a three-compartment model with a transit compartment for absorption. Covariates of body weight, sex, age, race, mild or moderate renal impairment, and mild hepatic impairment did not meaningfully explain variability in brigatinib exposure, thereby suggesting that no dose adjustments are required based on these covariates.