Possibilities to decrease the absorber thickness reducing optical and recombination losses in CdS/CdTe solar cells

Abstract

Based on the optical constants, calculations of optical losses in CdS/CdTe solar cells have been carried out taking into account reflections at the interfaces and absorption in the TCO and CdS layers. It has been shown that the losses caused by reflections at the interfaces result in lowering the short-circuit current by ~9 %, whereas absorption in the TCO and CdS layers with the typical thicknesses lead to losses of 15–24 %. Calculations of the integrated absorptive capacity of CdTe layer taking into account the spectral distributions of the standard AM1.5 solar radiation and the absorption coefficient of CdTe have been carried out. It is shown that in CdTe, the almost complete absorption of photons (≥99.9 %) in the hv > E_g range is observed at a layer thickness of more than 20–30 μm, and the absorptive capacity of photons in a CdTe layer of thickness 1 μm is about 93 %. Based on the continuity equation and taking into account the recombination at the front and rear surfaces of the CdTe layer as well as in the space charge region, the restrictions imposed on the thickness of the absorber layer in CdS/CdTe heterojunction are studied. In all cases, along with the mobilities and lifetimes of charge carriers, the concentration of uncompensated impurities in CdTe plays a key role in the generation of photocurrent. When the CdTe absorber layer is thin (<1 μm), it is impossible to avoid a noticeable decrease of the short-circuit current density. The losses of the short-circuit current are equal to 19–20 % when the thickness of the CdTe layer is 0.5 μm whereas only 5 % for a typical thickness of 2–3 μm.

Introduction

In recent years, photovoltaics (PV) demonstrates the highest growth rate in the entire energy sector despite the global financial crisis. For the next years the growth rate is expected to be also quite high. However, the PV contribution based mostly on silicon wafers by more than 90 % is less than 0.5 % in the global energy system. The contribution of PV solar power plants in generation capacity in the world will reach ~1 % only in the years 2018–2020 and may exceed 10–15 % in the years 2045–2050 [1–3].¹ The prospects for so desired rapid development of PV are not reassuring. Thus, solving the energy problems by developing Si PV seems too lengthy under the conditions of the approaching global warming.

The reason for the slow power growth of traditional Si solar modules lies in large consumption of materials and energy, high labor intensiveness and, as a consequence, in low productivity and high cost of modules with acceptable PV conversion efficiency for mass production [4, 5]. The problem is fundamental and lies in the fact that silicon is an indirect semiconductor and, therefore, the total absorption needs its significant thickness (up to 0.5 mm or more). As a result, to collect the charge photogenerated in a thick absorbing layer, considerable diffusion length of minority carriers and, therefore, high quality material is required for the solar module production.

A radical way to reduce the cost of solar modules and to increase drastically the volume of their production is the transition to thin-film technology based on direct-gap semiconductors deposited on a cheap large-area substrate (glass, metal foil, plastic). The direct-gap semiconductor can absorb solar radiation with a thickness, which is about 10² times less than the thickness of the mono- or polysilicon wafer. Thus, the transition from crystalline silicon to direct-gap semiconductors leads first of all to noncomparable less consumption of photoelectrically active material used in the solar cell.

High absorptivity of a direct-gap semiconductor has also an important consequence with respect to the quality of material used in solar cells. Since the direct-gap semiconductor can absorb solar radiation at its thickness much smaller than that of the Si wafer (or ribbon), the requirements for chemical purity and crystalline perfection of the absorber layer become much weaker. Indeed, to collect photogenerated charge carriers, it is necessary to have a diffusion length of minority carriers in excess of the thickness of the absorber layer. It follows from this that in the solar cell based on direct-gap semiconductor, the diffusion length L may be about 2 orders smaller, i.e. the carrier lifetime τ can be shorter by 4 (!) orders of magnitude (L ~ τ^1/2) compared with silicon. Thus, the manufacture of thin-film solar modules based on the direct-gap semiconductors does not require high purification and crystallinity of the material as it is needed in the production of modules based on crystalline, polycrystalline, or ribbon silicon.

Thin-film technology has a number of other significant advantages. While Si devices are manufactured from wafers or ribbons and then processed and assembled to form modules, in thin-film technology many cells are simultaneously made and formed as a module. The layers of solar cells are deposited sequentially on moving substrates in a continuous highly automated production line (conveyor system) and, importantly, at temperatures not exceeding 200–650 °C compared with 800–1,450 °C for the main processes of c-Si or m-Si. This minimizes handling and facilitates automation leading to the so-called monolithic integration.

Thus, thin-film solar modules offer the lowest manufacturing costs and are becoming more prevalent in the industry because they allow improving manufacturability of the production at significantly larger scales than for wafer or ribbon Si modules. Therefore, it is generally recognised that the contribution of thin-film technology in solar energy will be to grow from year to year faster. Many analysts believe that it is only a matter of time before thin films would replace Si wafer-based solar cells as the dominant photovoltaic technology. It should be noted that experts and managers of some silicon PV companies long ago have come to conclusion that there will be serious limitations for growing their wafer silicon business by simply expanding in the future [6]. All of these companies are researching wafer-Si alternatives including the thin-film technologies and are already offering such commercial thin-film modules.

It is, however, necessary to agree that solar cells of all types on Si wafers (representatives of the so-called first generation photovoltaics) will maintain their market position in the future. In hundreds of companies around the world, one can always invest (with minimal risk) and implement the Si technology developed for microelectronics with some modifications. Mono- and polycrystalline Si wafers, which are used in the semiconductor industry, can be made into efficient solar cells with full confidence. It is also important that Si is very abundant, clean, nontoxic, and very stable. However, due to limitations in production in large volumes of Si for solar modules often-expressed projections for significant increase in their contribution to the world energy system in the coming years are highly questionable.

Unquestionable leaders in thin-film technologies are solar cells on amorphous silicon (a-Si), copper-indium-gallium diselenide (CuIn _x Ga_1−xSe₂), and cadmium telluride (CdTe), whose market share is expanding every year [7]. It should be noted that compared with other thin-film materials, technology of CdTe solar modules is simpler and more suitable for large-scale production. Since the past decade, polycrystalline thin-film CdS/CdTe solar cells fabricated on glass substrates have been considered as one of the most promising candidates for large-scale applications in the field of PV energy conversion [8, 9]. The growth rate of solar PV industry based on thin-film CdTe solar cells is higher than any other PV technologies. Solar power plants based on CdTe with capacities of several tens of megawatts have already been built in Germany, Spain, Canada, the United States, and other countries. Agreements have been concluded on the construction of CdTe power plants with a capacity of an order of magnitude higher in the U.S. and even two orders of magnitude greater in China.

PV conversion efficiency of small area laboratory samples of CdS/CdTe solar cells exceeds 17 % [10]. The efficiency of large area CdTe solar modules is markedly inferior to that of silicon analogues until recently, but every year, this key indicator is continuously increasing and had already reached 14.4 % for some samples of modules in early 2012 [11]. Today the challenge facing the researchers and technologists is how to increase the efficiency of current large area CdS/CdTe modules decreasing the gap between the current efficiency and the theoretical limit of 28–30 % [12–14].

The present paper reports the theoretical study of optical and recombination losses, which are important causes of low efficiency of CdS/CdTe solar cells. The first part of the paper focuses on optical losses due to absorption and reflection at the interfaces in the device. It seems that the results of these calculations are interesting from a scientific and practical point of view, since they suggest possible ways to increase the efficiency of CdS/CdTe solar cells by reducing the optical losses, and vice versa they show in which cases a decrease in the optical losses gives only a small gain. The second part of the paper is devoted to a detailed study of recombination of charge carriers at the front and rear surfaces of the CdTe absorber layer, as well as in the space charge region of CdS/CdTe heterostructure. It is shown that the concentration of uncompensated impurities (defects), which determines the width of the space charge region is one of the key parameters of the material used as an absorber in the solar cell (of course, in addition to the lifetimes and mobilities of charge carriers). The most current practical issues with respect to minimizing the thickness of the absorber CdTe layer are also considered taking into account the influence of the above-mentioned factors. The importance of this aspect arises from the fact that one limiting factor for the terawatt production of CdTe modules in the future may be the scarcity of tellurium.

It should be noted that this study is a generalization of the results presented in some our previous publications [15–18]. The quantitative characteristics of optical and recombination losses are presented for the first time.

Optical losses in thin CdS/CdTe solar cells

In the literature there are a good amount of experimental data on the optical transmission of the glass/TCO(ITO or SnO₂:F) and glass/TCO/CdS structures that provide information about the losses caused by reflection from the interfaces and absorption in the glass, ITO, SnO₂:F, and CdS layers [19–21].² However, in the case of glass/TCO structure, the surface of TCO layer is in optical contact with air, rather than with CdS, as in the real case. In the case of glass/TCO/CdS structure, the surface of CdS is in contact with air rather than with the CdTe layer. As shown below, measuring the transmission of the glass/TCO and glass/TCO/CdS structures leads to the results, which differ significantly from those measured on the real structure of the solar cell. Further, in the literature, pronounced interference oscillations in the transmission curves are always observed, which are also relatively stronger than in the real device structure.

“Optical losses in thin CdS/CdTe solar cells” focuses on optical losses due to reflection at the interfaces and absorption in ITO, SnO₂:F, and CdS layers. Calculations have been carried out based on the optical constants of materials used (the refractive index and extinction coefficient).

Reflection losses

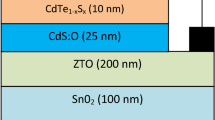
The sketch of a typical glass/TCO/CdS/CdTe solar cell is shown in Fig. 1. Before reaching the photoelectrically active CdTe absorber layer, solar radiation penetrates the glass plate, the TCO layer and the CdS window layer. Obviously, this is accompanied by optical losses upon reflection from the interfaces air–glass, glass–TCO, TCO–CdS, CdS–CdTe as well as absorption in glass plate, TCO and CdS. According to the Fresnel equations, when the light is at near-normal incidence, the reflection coefficient (reflectivity) from the interface between two contacting transparent materials is determined by their refractive indices n₁ and n₂:

$$ R = \left( {\frac{{n_{1} - n_{2} }}{{n_{1} + n_{2} }}} \right)^{2} . $$

(1)

Fig. 1

Schematic cross-section of thin-film CdS/CdTe solar cell

In the case of electrically conductive materials, the refractive index contains an imaginary part and can be written as n* = n − iκ, where n is the refractive index, and κ is the extinction coefficient $(i = \sqrt { - 1} )$. The reflection coefficient from the interface is defined as the square of the modulus of $(n_{1}^{*} - n_{2}^{*} )/(n_{1}^{*} + n_{2}^{*} )$ and has the form [22]:

$$ R = \frac{{\left| { \, n_{1}^{*} - n_{2}^{*} \, } \right|^{2} }}{{\left| {n_{1}^{*} + n_{2}^{*} } \right|^{2} }} = \frac{{(n_{1} - n_{2} )^{2} + (\kappa_{1} - \kappa_{2} )^{2} }}{{(n_{1} + n_{2} )^{2} + (\kappa_{1} + \kappa_{2} )^{2} }}. $$

(2)

At the air–glass interface we will find the reflection coefficient R₁₂ (see Fig. 1) taking n₁ = 1, and κ₁ = 0 for the air. For the convenience of presenting the main optical losses, we first assume that for glass κ₂ = 0. This is justified by the fact that in photovoltaic applications, specialized glass is often used with low iron oxide content, where the absorption is observed only in the ultraviolet region. As it will be shown later, absorption in the low-iron glass practically does not exhibit itself in short-circuit current (see “Effect of optical losses on short-circuit current”).

For the refractive index of glass n₁ we will use the Sellmeier (Zelmeer) dispersion equation applied for quartz (SiO₂) [23]:

$$ n^{2} = 1 + \frac{{a_{1} \lambda^{2} }}{{\lambda^{2} - \lambda_{1}^{2} }} + \frac{{a_{2} \lambda^{2} }}{{\lambda^{2} - \lambda_{2}^{2} }} + \frac{{a_{3} \lambda^{2} }}{{\lambda^{2} - \lambda_{3}^{2} }} , $$

(3)

where a₁ = 0.6962, a₂ = 0.4079, a₃ = 0.8974, λ₁ = 68 nm, λ₂ = 116 nm, and λ₃ = 9,896 nm.

To find the reflection coefficients at the interfaces glass–TCO, TCO–CdS, and CdS–CdTe it is necessary to know the values of the refractive index and extinction coefficient of TCO, CdS, and CdTe in the spectral range 300–850 nm. In the discussion below we consider the two most common structures of CdS/CdTe solar cell in which indium tin oxide (ITO) and F-doped tin oxide (SnO₂:F) are used as TCO. Figure 2 shows the spectral dependences of n and κ for ITO (typically 90 % In₂O₃, 10 % SnO₂) taken from Ref. [24, 25] and for SnO₂:F taken from Ref. [26]. Figure 2 also shows the data on CdS [27] and CdTe [28].

Fig. 2

Refractive index (a), and extinction coefficient (b) of SiO₂, ITO, SnO₂:F, CdS and CdTe as a function of wavelength (the curves κ(λ) for glasses can be seen in Fig. 7)

Note that the data on the optical constants of the materials cited in various sources differ somewhat, depending on the method adopted to grow the crystal or film. However, with a few exceptions, these differences manifest themselves weakly in the calculation results of the integral characteristics of a multilayer solar cell, which is short-circuit current J_sc. For example, calculations of J_sc using data for n and κ, obtained by ellipsometry for CdTe single crystal and films [28] lead to almost identical results.

Figure 3 shows the spectral dependence of the reflection coefficients R(λ) at the interfaces calculated by substituting n and κ from Fig. 2 into Eq. (2). Emphasis is given on obtaining low reflection coefficients (less than 0.05–0.06 in the entire spectral range). The explanation for this is a relatively small difference between the optical constants of contacting materials. The calculation results shown in Fig. 3b for reflection at the interfaces of the same materials with air give the usually observed values of R, for example, R = 0.037–0.034 for the air/glass interface, R = 0.25–0.35 for the air/CdTe interface, etc.

Fig. 3

Reflection coefficients R for the interfaces: air–glass (SiO₂), glass–ITO, glass–SnO₂, ITO–CdS, SnO₂–CdS, CdS–CdTe (a); and air–SiO₂, air–ITO, air–SnO₂, air–CdS, air–CdTe (b)

As a consequence of the conservation of energy, the transmission coefficient (transmission) in each interface is given by T = 1 − R. Therefore, for reflection losses at all interfaces before the solar radiation reaches the CdTe absorber layer, the transmission T(λ) can be calculated by the formula

$$ T(\lambda ) = (1 - R_{12} )(1 - R_{23} )(1 - R_{34} )(1 - R_{45} ), $$

(4)

where R₁₂, R₂₃, R_34, and R₄₅ are the reflection coefficients of the interfaces: air–glass, glass–ITO (or glass–SnO₂), ITO–CdS (or SnO₂–CdS), and CdS–CdTe, respectively (see Fig. 1). As stated earlier, we consider normal incidence of the rays. As will be explained below, the multiple reflections of rays have an insignificant effect due to the relatively close values of the refractive indices of the contacting materials.

It follows from Fig. 4 that the overall reflection losses at the interfaces air–glass, glass–ITO, ITO–CdS, and CdS–CdTe amount to about 9 % in the entire spectral range 300–850 nm. This implies that the reflection losses in the case of thin-film CdS/CdTe structure are not as critical as in the case of a silicon solar cell. In fact, the coefficient of reflection from the mirror surface of silicon is at least 30 %, while in the region λ < 400 nm they are even higher than 50 %.

Fig. 4

Calculated transmittance T(λ) and reflectance R(λ) of the glass/ITO/CdS (solid line) and glass/SnO₂/CdS (dashed line) structures considering only reflections from all interfaces

Accounting for absorption losses

The data for the extinction coefficient κ(λ) shown in Fig. 2b allows to find the absorption coefficient as

$$ \alpha (\lambda ) = \frac{2\omega }{c}\kappa = \frac{4\pi }{\lambda }\kappa , $$

(5)

where ω = 2πv is the angular frequency, and c is the speed of light in free space.

Knowing α(λ) for the CdS and ITO (SnO₂), the absorption in these layers can be taken into account by incorporating in Eq. (4) the addition factors exp[−α_CdS(λ)d_CdS], exp[−α_ITO(λ)d_ITO], exp[−α_SnO(λ)d_SnO]:

$$ T(\lambda ) = (1 - R_{12} )(1 - R_{23} )(1 - R_{34} )(1 - R_{45} )\exp ( - \alpha_{\text{SnO}} d_{\text{SnO}} )\exp ( - \alpha_{\text{CdS}} d_{\text{CdS}} ), $$

(6)

or

$$ T(\lambda ) = (1 - R_{12} )(1 - R_{23} )(1 - R_{34} )(1 - R_{45} )\exp ( - \alpha_{\text{ITO}} d_{\text{ITO}} )\exp ( - \alpha_{\text{CdS}} d_{\text{CdS}} ), $$

(7)

where d_ITO, d_SnO, and d_CdS are the thicknesses of the ITO, SnO₂:F, and CdS layers, respectively.

Figure 5 shows the transmission of the glass/ITO/CdS structure (solid lines) and the glass/SnO₂/CdS structure (dashed lines) calculated with various thicknesses of the ITO, SnO₂:F, and CdS layers.

Fig. 5

Transmission of the glass/ITO/CdS (solid lines) and glass/SnO₂/CdS (dashed lines) structures calculated a at d_CdS = 100 nm and different thickness of ITO and SnO₂:F and b at d_ITO = d_SnO = 200 nm and different thickness of the CdS layer

As can be seen in Fig. 5, in addition to reflection, appreciable losses (10–15 %) are observed in the wavelength range λ > 500–550 nm caused by absorption in SnO₂:F and greater losses (15–35 %) in the case of ITO. Much more losses are observed in the region λ < 500–550 nm caused by absorption in CdS together with ITO or SnO₂:F. In the wavelength region λ > 500–550 nm, by thinning the ITO it is possible to reduce the optical losses by 12–15 %; however, the effect of SnO₂:F thickness is only nominal. Greater effect can be achieved in the λ < 500–550 nm range by decreasing the thickness of the CdS layer. However, to obtain uniform CdS layer without discontinuities (known as ‘pinholes’) is difficult. The thickness of CdS about 50–60 nm is apparently close to the minimum possible value with the current technology used in the manufacture of CdS/CdTe solar cells [29].

Let us consider the errors caused by neglecting the multiple reflections and the interference effects in the TCO and CdS layers leading to the oscillations observed typically in the transmission curves of the glass plate covered with thin TCO or CdS layer. As is known, the transmission of a transparent film of thickness d with refractive index n at normal incidence taking into account the interference is given by the equation widely known in optics as the Airy formula for multiple beam interference in a system of two parallel plane reflecting surfaces for the case of no absorption [30]:

$$ T(\lambda ) = \frac{{(1 - R)^{2} }}{{(1 - R)^{2} + 4R\sin^{2} (4\pi \,nd/\lambda )}}, $$

(8)

where R is the reflection coefficient of the film surface.

In Eq. (8), it is assumed that the film is in contact with identical materials at both sides. From our point of view, interference effects appear considerably weaker if the film is in contact with materials having refractive index higher than that of air. As an example, Fig. 6 shows the calculation results obtained with Eq. (8) for the transmission of ITO layer, when it is in contact with air (solid oscillating line) and in contact with SiO₂ (dashed oscillating line).

Fig. 6

Transmittance of the ITO film (d = 200 nm) (1) in air calculated by Eq. (8) (oscillating solid line1), (2) contacted from both sides with SiO₂ and calculated by Eq. (8) at R = R₂₃ (oscillating dashed line 2), (3) the same but calculated as [1 − R₂₃(λ)]² (monotonically varying dotted line3)

As can be seen, a pronounced oscillating interference behavior of T(λ) is observed in both cases. However, as expected, in the case of reflection from ITO/SiO₂ interface, the amplitude of the oscillation is 5–7 times smaller, which is explained by a smaller difference in the refractive index and extinction coefficient of the materials at the interface.

In Fig. 6, transmission of the ITO layer (dotted line 3, without oscillation) is calculated as T(λ) = (1 − R₂₃)² (R₂₃ is the reflection coefficient at the ITO–SiO₂ interface), i.e. without taking into account multiple reflections. It is seen that the average transmission of the ITO film in contact with SiO₂ (dotted line 3) calculated using Eq. (8) and the curve T(λ) = (1 − R₂₃)² is comparable in magnitude. It can be assumed that the calculation results of short-circuit current density (presented below) as an integrated characteristic calculated over a broad spectral range, may vary slightly in these two cases. Thus, the interference effects in the solar cells under study appear to be rather weak, i.e. they contribute only a minor error in the results of the short-circuit current calculation.

Effect of optical losses on short-circuit current

Calculation of short-circuit current J_sc can quantitatively account for the effect of optical losses in the whole spectral range. We will calculate J_sc for AM1.5 total solar radiation using the Table ISO 9845-1:1992 [31].

If Φ _i is the spectral radiation power density and hν is the photon energy, the spectral density of the incident photon flux is Φ _i /hν _i can be written J_sc as

$$ J_{\text{sc}} = q\sum\limits_{i} {T(\lambda_{i} )\frac{{\Upphi_{i} (\lambda_{i} )}}{{hv_{i} }}} \Updelta \lambda_{i} , $$

(9)

where ∆λ _i is the wavelength range between the neighboring values of λ _i in the table and the summation is over the spectral range λ = 300 nm to λ = λ_g = hc/E_g ≈ 840 nm.

It should be noted that solar radiation reported in the Table ISO 9845-1:1992 is with 0.5 nm interval in the range 300–400 nm and 1 nm interval in the range 400–1,500 nm. Therefore, replacing Φ _i and α _i in Eq. (9) with their average values in the interval Δλ _i , i.e. (Φ _i  + Φ_i+1)/2 and (α _i  + α_i+1)/2, leads to almost imperceptible changes in the results of calculations of J_sc.

Figure 7a shows the dependence of short-circuit current J_sc on the thickness of ITO and SnO₂:F calculated for different thickness of CdS with the assumption that the efficiency of photoelectric conversion in the CdTe layer is equal to 100 %. Figure 7b shows the percentage decreases of J_sc. In this case, the value of the optical losses is found using the expression

$$ \Updelta J_{\text{sc}} (\% ) = \frac{{J_{\text{sc}}^{\text{o}} - J_{\text{sc}} }}{{J_{\text{sc}}^{\text{o}} }} \times 100\,\% , $$

(10)

where $J_{\text{sc}}^{\text{o}}$ is the short-circuit current density found by Eq. (9) at T(λ) = 1 ($J_{\text{sc}}^{\text{o}} = 29.7\,{\text{mA}}/{\text{cm}}^{2}$ according to the Table ISO 9845-1:1992).

Fig. 7

a Effect of optical losses on short-circuit current depending on the thickness of ITO and SnO₂:F layer calculated for different thicknesses of CdS layer (100 % photoelectric conversion efficiency in the CdTe absorber layer is assumed); b the same but expressed in percents

As can be seen in Fig. 7, optical losses caused by TCO layer with thickness of 200 nm are about 20 and 10 % for ITO and SnO₂:F, respectively. When the thickness of the TCO layer is close to 0, the optical losses are caused only by reflection and become equal to 8.5 and 8.8 % for the SnO₂:F and ITO layers, respectively. Thicker ITO layers of 500–700 nm leads to unacceptably high optical losses (~40 % at d_CdS = 0), while using SnO₂:F the losses are only ~15 % (at d_CdS = 0). In both cases, the presence of CdS layer, even when its thickness is 50 nm (close to the practically minimum possible value [29]) leads to an additional increase in the optical losses by approximately 10 %. When the CdS thickness is 100 nm, the additional losses for ITO and SnO₂ are ~12 and 17 %, respectively. In the case of SnO₂:F, the presence of very thin CdS layer limits J_sc at ~23 mA/cm². The achievement of this value in ITO/CdS/CdTe solar cell is possible only with an ultra-thin ITO layer.

It is evident from the data obtained that a short-circuit current density above ~25 mA/cm² is practically impossible with the use of CdS as the window layer since the band gap is only 2.42 eV (300 K). However, slightly higher current (J_sc ≈ 26 mA/cm²) can be obtained with the use of modified CdS-based films with wider band gap. In TCO/Zn₂SnO₄/CdS/CdTe devices, for example, inter-diffusion between the CdS and Zn₂SnO₄ (ZTO) films effectively “consumes” the relatively thick CdS film during device fabrication [32, 33].

Another option for improving the charge collection in the short-wavelength region is the use of a wider band gap Cd_1−xZn _x S ternary alloy to replace CdS as the window layer [34]. Results of the calculations show that integrating a ZTO buffer layer into a CdTe cell with the intention of modifying the TCO layer (rather than CdS) results in a very insignificant increase in J_sc, since the optical losses in the TCO are mainly due to reflection rather than absorption.

Until now, losses due to absorption in the glass were not considered because it was assumed that they are insignificant. Let us estimate the error, which we allowed.

It is well known that the most common glasses contain iron impurities in the form of iron salts within the silicon oxide that impede the transmission of light through the material. Because of this, apart from a fairly strong absorption in the UV, there is also a noticeable absorption in the visible and infrared spectral range. However, there are glasses with low iron oxide content, the so-called low-iron solar glass with high transmittance above 91.6 % and the virtual absence of color. Figure 8 shows the optical transmission of low-iron glass produced by Stanley Glass Co. Ltd. for PV modules [35].

Fig. 8

Spectral distribution of the transmissions T and absorption coefficient α_glass of low-iron glass

Knowing the transmission of the glass T(λ), one can find the spectral dependence of its absorption coefficient α_glass. Since the coefficient of reflection from the glass surface R₁₂ is small (~4 %), to find α_glass the formula which does not take into account multiple reflections from the surfaces of the plate can be used [36]:

$$ \alpha_{\text{glass}} = \frac{1}{{d_{\text{glass}} }}\ln \left[ {\frac{{(1 - R_{12} )^{2} }}{T(\lambda )}} \right], $$

(11)

where d_glass is the glass thickness.

The spectral dependence of the absorption coefficient α_glass, found from the transmission curve using the formula (11), is shown in Fig. 8. As can be seen, the absorption coefficient of low-iron solar glass is lower by several orders than those for ITO, SnO₂, CdS, and CdTe. But one should keep in mind that the thickness of the glass in the CdS/CdTe solar cell (typically 3.2 mm) is at least three orders of magnitude greater than that of the thin-film device components.

To account for the absorption of glass in the calculation of short-circuit current density J_sc it is necessary to introduce in the expressions for the transmissions Eq. (6) and (7) a factor exp[−α_glass(λ)d_glass]. The calculations of J_sc show that taking into account the optical absorption in the 3.2-mm thick low-iron glass reduces J_sc by no more than ~0.5 %. This corresponds to a decrease in the value of J_sc by ~0.1 mA/cm² at a thickness of 300 μm for ITO or SnO₂. Thus, optical losses due to absorption in the low-iron glass can be ignored without introducing appreciable error that was made in the above calculations.

As seen in Fig. 3, the reflection coefficient R₁₂ is very weakly dependent on λ averaging about 3.5 % and the contribution of the extinction coefficient (κ = α_glassλ/4π = 10⁻⁷–10⁻⁵) to R₁₂ is negligible according to Eq. (2) (see Fig. 7b). Therefore, we can say that the application of anti-reflective coating on the front surface of the glass can result in the ideal case in an increase in the short-circuit density of ~3.5 %, which corresponds to ~0.7 mA/cm².

Limitation of efficiency due to insufficient absorptive capacity of the CdTe layer

Calculating the short-circuit current in the previous sections, we assumed 100 % efficiency of photoelectric conversion in the CdTe layer. In fact, the efficiency of the solar cell is limited by the processes in CdTe. In addition to recombination at the surfaces and in the space charge region (SCR), the loss of an optical nature related to the insufficient absorptive capacity of the CdTe layer also takes place.

In this section, calculations are made for the exact values of integrated absorptive capacity of the CdTe layer when the spectral distribution of solar radiation and the absorption coefficient of the material are taken into account. It should be noted that the literature does not pay adequate attention to this factor. Meanwhile, consideration of the absorbance becomes particularly relevant in connection with the desire to reduce the thickness of the absorber layer in CdS/CdTe solar modules, i.e. to develop the devices with ultra-thin CdTe layer [37–41]. In this case, the optical losses in the absorber layer can be significant. As shown below, the losses due to the lack of absorptive capacity of the CdTe layer with a thickness of, for example, 0.5 μm are about 13 %.

As earlier, the losses of pre-penetrating radiation in CdTe layer can be taken into account by the introduction of the factor T(λ), which represents the optical transmission of the glass substrate with layers of TCO and CdS. Thus, the expression for the integrated (rather than at a certain wavelength) absorptivity of solar radiation, which has reached the CdTe layer with a thickness d, can be represented as (at normal incidence of the rays):

$$ A_{\Upphi } (d) = \frac{{\sum\nolimits_{i} {T(\lambda )\Upphi_{i} [1 - \exp ( - \alpha_{i} d)]} \Updelta \lambda_{i} }}{{\sum\nolimits_{i} {T(\lambda )\Upphi_{i} } \Updelta \lambda_{i} }}, $$

(12)

where α _i is, as earlier, the absorption coefficient of CdTe at wavelength λ _i ; Φ _i is the spectral power density of radiation at wavelength λ _i [31].

The AM1.5 spectral distribution of solar radiation Φ(l) and the absorption curve a(l) of CdTe are shown in Fig. 9, where the wide range of variation of Φ(l) and a(l) in the working ranges of l are illustrated. For α(λ) we used the data given in [41] and supplemented by the results of our measurements at the absorption edge [42]. For the optical transmission T(λ) of SnO₂:F (d = 200 nm) and CdS (d = 50 nm) the date obtained in “Accounting for absorption losses” can be used, i.e. the T(λ) transmission is given by Eq. (6). The summation in Eq. (12) should be taken from λ = 300 nm to λ = λ_g = hc/E_g, where E_g is the band gap of CdTe equal to 1.47 eV at 300 K [42].

Fig. 9

Power spectral density of solar radiation Φ(λ) under standard conditions of AM1.5 and the absorption curve α(λ) for CdTe

Figure 10a shows the absorptivity of solar radiation A_Φ as a function of the thickness of CdTe calculated by Eq. (12) using the data on α(λ), Φ(λ) and the transmission of the glass/TCO/CdS structure T(λ). Let us emphasize that the solid line shows how the absorptivity of solar radiation power increases with increasing the thickness of CdTe. In this case, one does not take into account that an electron–hole pair arises independently of the photon energy absorbed in the range from 1.47 to 4.1 eV (the latter corresponds to a wavelength of 300 nm). For this reason, the number of electron–hole pairs, and hence the short-circuit current generated in the solar cell is not proportional to the power of solar radiation. Obviously, in the context of the discussed issue, it is more correct to handle with the flow of photons rather than the power of solar radiation.

Fig. 10

a Dependence of absorptivity of solar radiation power A_Φ and absorptivity of photon flux A_hv in the solar radiation AM1.5 (hv ≥ E_g) on the thickness of the CdTe layer. b Optical losses due to incomplete absorption depending on the thickness of the CdTe layer. Curves A_hv(d) and A_hv(2d) are without and with taking into account 100 % reflections from the back surface, respectively

As mentioned earlier, the photon number in the spectral interval Δλ _i can be obtained by dividing the power of radiation in this spectral range Φ _i Δλ _i by the photon energy hv _i . As a result, the expression for the absorptivity of the photon flux in the solar radiation A_hv takes the following form:

$$ A_{\text{hv}} (d) = \frac{{\sum\nolimits_{i} {T(\lambda )\frac{{\Upphi_{i} }}{{hv_{i} }}[1 - \exp ( - \alpha_{i} d)]} \Updelta \lambda_{i} }}{{\sum\nolimits_{i} {T(\lambda )\frac{{\Upphi_{i} }}{{hv_{i} }}} \Updelta \lambda_{i} }}. $$

(13)

The calculated dependence of the absorptivity on the thickness of CdTe for the photon flux A_hv in the solar radiation AM1.5 is shown in Fig. 10a by the dashed line. As expected, for small d the fraction of absorbed photons in the solar radiation A_hv is less than the fraction of absorbed radiation power A_Φ. This is understandable, because in a thin layer the probability of high-energy photon absorption is greater than that of the low-energy photons and there are less high-energy photons per unit of radiation power. With increasing d the curves A_Φ(d) and A_hv(d) converge and coincide at a thicknesses d, where the total absorption of radiation energy and all of the photons occurs (hv ≥ E_g).

It follows from the results shown in Fig. 10a that the total photon absorption in CdTe is observed at a layer thickness of 60–70 μm (99.9 % at a thickness of 20–30 μm), although very often in the papers devoted to CdTe solar cells it is assumed that this occurs at a thickness of the CdTe layer of several microns. Such an assumption usually rests on the argument that in CdTe, as a direct-gap semiconductor, the value of α in the fundamental absorption region exceeds 10⁴–10⁵ cm⁻¹, i.e. effective penetration depth of radiation α⁻¹ is less than 1 μm (see, e.g. [42–44]). Our calculations, taking into account the spectral distribution of the absorption coefficient of CdTe and the standard solar radiation AM1.5, show that in fact the absorptivity of photons in the CdTe layer with a thickness of 2–3 μm is about 97 % and only ~93 % for a layer thickness of 1 μm.

It should also be borne in mind that most often a metal electrode is applied to the back surface of the CdTe absorber layer with the result that radiation with low absorption coefficient is reflected from such an interface. In this case with 100 % reflectance from the back surface the absorptivity is the same as for the double thickness of the absorber layer, i.e. the A_hv(d) value in such a solar cell can be found by doubling the thickness d in Eq. (13). The calculation results in Fig. 10b show that in this case to ensure complete absorption of photons in the solar radiation, the CdTe layer should also be thick enough, i.e. greater than 40–50 μm. If, for example, 95 % absorptivity in solar cell is to be accepted as an acceptable value, the thickness of the CdTe layer with a mirror back surface should be equal to ~0.7 μm rather than ~1.4 μm as in the case when the reflection from the back surface is not used.

It is pertinent to note that the absorptivity of CdTe even at 100 % reflection from the rear surface of the CdTe layer is significantly reduced with a further thinning the CdTe layer. For example, at d = 0.5 μm the optical loss is equal to 7 and 12 % at d = 0.3 μm.

Recombination losses and requirements imposed on thickness of the CdTe layer

In papers devoted to the CdS/CdTe solar cells with extremely thin CdTe absorber layer, the limitations imposed on short-circuit current density, open circuit voltage, fill factor, and, ultimately, the efficiency of the solar cell are discussed. One of the omissions in the analysis of CdS/CdTe solar cells is disregard such an important parameter as the width of the space charge region (SCR). One cannot argue against the fact that the width of the SCR (rather than just the thickness of CdTe) has a significant effect on the carrier collection and hence the photocurrent in the CdS/CdTe heterostructure as in any solar cell or photodiode. In fact, the electric field in the SCR ensures efficient collection of carriers photo-generated in the SCR as well as the charge reaching the SCR by diffusion from the neutral part of the CdTe. In addition, when the SCR is narrow, the strong electric field acting near the front surface (close to CdS) of the CdTe layer prevents recombination of carriers generated near the surface; however, when the SCR is wide, there can be significant reduction in photocurrent. Finally, the losses due to recombination of photogenerated electron–hole pairs in very SCR depend on its width. The results presented in our previous publications show that for a given thickness of the CdTe absorber layer, the changes of the SCR width truly can significantly affect the processes in the CdS/CdTe solar cell [45, 46]. In this section, the most practical issues with respect to minimizing the thickness of the absorber CdTe layer are considered taking into account the influence of the above-mentioned factors.

Like the optical losses, a quantitative description of losses caused by recombination at the front and back surfaces of the CdTe layer, as well as in the space charge region (SCR), can be obtained by calculating the short-circuit current density J_sc. In general, the J_sc is described by

$$ J_{\text{sc}} = q\sum\limits_{i} {T(\lambda_{i} )\frac{{\Upphi_{i} (\lambda_{i} )}}{{hv_{i} }}\eta (\lambda_{i} )} \Updelta \lambda_{i}, $$

(14)

where η(λ _i ) is the monochromatic photoelectric quantum efficiency at wavelength λ _i , and T(λ) is, as earlier, the optical transmission of the glass substrate with layers of TCO and CdS.

It is known that the thin CdS film in CdS/CdTe heterostructure does not contribute to the photoelectric conversion, but only serves as a “window”, through which the radiation is introduced into the CdTe absorber layer. Therefore, the photocurrent in the CdS/CdTe solar cell is generated only in the CdTe layer. It should also be noted that CdS is a rather thin low-resistivity low-compensated n-type semiconductor, so that the SCR is located practically only in the p-CdTe layer (see, e.g. [8, 47]). So, for the CdS/CdTe heterostructure, a schematic energy-band diagram of an abrupt asymmetric p-n junction or a Schottky diode can be applied (Fig. 11).

Fig. 11

Schematic energy-band diagram of CdS/CdTe heterostructure without electron reflector near the back surface of CdTe

Quantum efficiency of a solar cell always includes the drift and diffusion components, which are result of photogeneration of electron–hole pairs in the SCR and the neutral part(s) of the diode structure, respectively.

Considering the drift component, it is necessary to take into account losses due to recombination at the interface of CdS with CdTe, i.e. at the front surface of the CdTe layer. The solution of the continuity equation in this case is cumbersome, but with respect to the considered heterostructure with sufficient accuracy it can be reduced to a simpler expression [45]:

$$ \eta_{\text{drift}} = \frac{{1 + \frac{{S_{\text{f}} }}{{D_{\text{p}} }}\left( {\alpha + \frac{2}{W}\frac{{\varphi_{\text{o}} - qV}}{kT}} \right)^{ - 1} }}{{1 + \frac{{S_{\text{f}} }}{{D_{\text{p}} }}\left( {\frac{2}{W}\frac{{\varphi_{\text{o}} - qV}}{kT}} \right)^{ - 1} }} - \exp ( - \alpha W), $$

(15)

where S_f is the velocity of recombination at the front surface of the CdTe layer, φ_o is the height of the barrier at the contact with CdS (Fig. 11) related to the diffusion potential V_bi by the reration φ_o = qV_bi, D_n is the diffusion coefficient of electrons related to their mobility μ_n by the Einstein relation qD_n/kT = μ_n, and W is the width of the SCR, which can be represented as [46]

$$ W = \sqrt {\frac{{2\varepsilon \varepsilon_{\text{o}} (\varphi_{\text{o}} - qV)}}{{q^{2} (N_{\text{a}} - N_{\text{d}} )}}} , $$

(16)

where ε is the relative permittivity of the semiconductor, ε_o is the electric constant, V is the applied voltage, and N_a − N_d is the concentration of uncompensated acceptors in the CdTe layer, which can differ by several orders of magnitude from the hole concentration in the valence band [45].

The diffusion component of the quantum efficiency η_dif is also found from the continuity equation. Taking into account recombination at the back surface of the CdTe layer and the boundary condition Δn = 0 at x = W, it can be written [44–48]

$$ \begin{aligned} \eta_{\text{dif}} & = \frac{{\alpha L_{\text{n}} }}{{\alpha^{2} L_{\text{n}}^{2} - 1}}\exp ( - \alpha W) \\ & \quad \times \left\{ {\alpha L_{\text{n}} - \frac{{\frac{{S_{\text{b}} L_{\text{n}} }}{{D_{\text{n}} }}\left[ {\cosh A - \exp \left( { - \alpha (d - W)} \right)} \right] + \sinh A + \alpha L_{\text{n}} \exp ( - \alpha (d - W))}}{{\frac{{S_{\text{b}} L_{\text{n}} }}{{D_{\text{n}} }}\sinh A + \cosh A}}} \right\}, \\ \end{aligned} $$

(17)

where A = (d − W)/L_n, D_n and L_n is the electron diffusion coefficient and diffusion length, S_b is the velocity of recombination at the rear surface of the CdTe layer, and d is the thickness of the CdTe layer.

The quantum efficiency η, appearing in Eq. (14) is the sum of drift and diffusion components:

$$ \eta = \eta_{\text{drift}} + \eta_{\text{dif}} . $$

(18)

The presence of W in Eqs. (15) and (17) reflects the significant impact of the SCR width (rather than only the thickness of the CdTe layer d) on the generation of the photocurrent in the CdS/CdTe heterostructure. As noted in the introduction to this section, the dependence of the efficiency of CdS/CdTe solar cell on W is usually not discussed in the papers dealing with the problem of minimizing the thickness of the CdTe absorber layer. The issue of uncompensated acceptor concentration N_a − N_d in a layer of CdTe, which determines according to Eq. (16) the width of the SCR, is not discussed as well.

As is known, the Poisson equation implies that the width of space-charge region in the diode structure is determined by the spatial distribution of space charge due to band bending. In the case of a semiconductor doped with one type of shallow impurity, the space charge density is independent of the x coordinate and determined by the concentration of majority carriers (n or p) in the bulk of the diode structure. However, CdTe always contains a lot of uncontrolled impurities and defects of the donor and acceptor types and is a semiconductor compensated to a greater or lesser degree. The conductivity of CdTe in CdS/CdTe solar cell is determined by the position of the impurity or defect energy levels in the band gap, near which the Fermi level is located. In contrast, the width of the SCR is determined by the concentration of uncompensated impurities (defects) N_a − N_d, which cannot be identified with the concentration of holes in the valence band p. The N_a − N_d and p values, as already noted, can differ by several orders of magnitude.

By varying the lifetimes of charge carriers and the concentration of uncompensated impurities, it is possible using Eqs. (15)–(17) to describe in detail all the variety of observed photoresponse spectra of CdS/CdTe solar cells. These equations also reflect the impact of the recombination of charge carriers at the CdTe surface layers on the photoelectric conversion efficiency. Below we show how recombination losses affect the value of short-circuit current density depending on the parameters of CdS/CdTe structure. In “Recombination losses at front surface of CdTe layer” and “Recombination losses in the SCR”, the dependence of the recombination losses on the width of the SCR and the material of CdTe absorber are studied. In order to eliminate the influence of the thickness of CdTe and recombination at its rear surface, the layer is considered to be sufficiently thick in this case. After determining the optimal width for the SCR, the effect of thickness of the CdTe layer on the short-circuit current density is investigated in “Losses due to decrease in the thickness of the CdTe layer and generalization of the results”.

Recombination losses at front surface of CdTe layer

Figure 12 shows the dependence of short-circuit current density of CdS/CdTe heterostructure on the width of the SCR calculated using Eqs. (15)–(17) under the conditions of AM1.5 (100 W/cm²) solar irradiation. Calculations were made for the surface recombination velocities S_f = 10⁷ cm/s and S_f = 0 at the front surface of the CdTe layer. The lifetimes of the charge carriers are assumed to be 10⁻¹⁰, 5 × 10⁻¹⁰ and 2 × 10⁻⁹ s based on the fact that, according to published data, the lifetimes of the charge carriers in thin-film CdTe are usually in the range from 10⁻¹⁰ s to 2 × 10⁻⁹ s [48–50]. In calculations we use the mobilities of electrons and holes, which in thin-film CdTe are often taken to be 320 and 40 cm²/(V s), respectively [51, 52]. The thickness of CdTe layer d is accepted to be 10 μm, when, as will be shown below, the thickness and the rear surface recombination have practically no effect on results of the calculations.

Fig. 12

a The dependence of short-circuit current density J_sc on the width of the space-charge region W calculated for different lifetimes of the electrons τ_n and the velocity of recombination at the front surface S_f = 0 (solid lines) and S_f = 10⁷ cm/s (dashed lines). b Recombination losses at the front surface in percentage (S_f = 10⁷ cm/s)

For comparison, the curves obtained by taking the lifetimes of electrons and holes as 2 × 10⁻⁶ s, and their mobilities 1,100 cm²/(V s) and 100 cm²/(V s), respectively, which are typical for the most pure and perfect CdTe single crystals, are also shown in Fig. 12 [53]. The curves illustrate the major impact of the lifetime of charge carriers on the short-circuit current in CdS/CdTe solar cell.

The results in Fig. 12 show that the short-circuit current density J_sc increases with W in the region, where W is well below 1 μm for the carrier lifetimes of 10⁻¹⁰, 5 × 10⁻¹⁰ and 2 × 10⁻⁹ s. This is because with an increase of W more and more of the radiation is absorbed in the SCR, where the photogenerated electrons and holes are effectively separated by the electric field. For W → 10 μm and without recombination at the front surface (solid lines in Fig. 12a), the short-circuit current density J_sc continues to increase approaching the maximum possible value of 23.2 mA/cm², which corresponds to absorption in the SCR of almost all radiation passed through a glass substrate, SnO₂:F and CdS layers (Fig. 1b). Of course, the maximum possible value of the short-circuit current density can be higher than 23.2 mA/cm², if it is provided a more high transparency T(λ) of TCO and CdS layers.

When W is less than 1 μm (it is relevant in the light of the discussed problem), the short-circuit current density is much lower than the maximum possible value 23.2 mA/cm² even in the absence of surface recombination. The reason for this is the low mobility of minority carriers (electrons) and, especially, their short lifetime. Indeed, even if the lifetime of electrons is τ_n = 2 × 10⁻⁹ s, their diffusion length L_n = (τ_nD_n)^1/2 is approximately equal to 1 μm, i.e. photoelectrically beneficial region constitutes a small portion of the thickness of CdTe. If τ_n = 2 × 10⁻⁶ s and D_n = 27.5 cm²/s (as in single crystal CdTe), the value of L_n exceeds 70 μm and the value of J_sc becomes close to the maximum value 23.2 mA/cm² (at S_f = 0).

Taking into account the surface recombination (dashed lines in Fig. 12a), the increase in J_sc at W > 0.2–0.3 μm with widening the SCR begins to saturate and decrease with a further increase in W, since the electric field in the SCR is reduced and recombination at the front surface of CdTe is intensified. With the presence of surface recombination (S_f = 10⁷ cm/s) and the real lifetimes of charge carriers (0.1–2) × 10⁻⁹ s, maxima on the curves are observed when the width of the SCR is equal to 0.4–0.8 μm. Evidently, with increasing W the diffusion component of the photocurrent is playing a lesser role, because the electron diffusion length L_n, even at τ_n = 2 × 10⁻⁹ s is ~1 μm. Therefore, when W > 3–5 μm the calculated values of J_sc for different lifetimes of the charge carriers are close to each other. It should be noted that such an important fact as the presence of maximum on the dependence of the short-circuit current J_sc on the SCR width (or on the concentration of uncompensated impurities N_a − N_d) was substantiated in our previous works [44, 45].

To compare the effect of surface recombination with other kinds of losses, reduction of J_sc is conveniently being represented in percentages. This is shown in Fig. 12b. Notice that the losses in percentage do not depend on the lifetime of charge carriers. Of course, when the SCR expands (W > 0.1 μm), the recombination losses increase rapidly. At the maxima on the J_sc(W) curves (W = 0.4–0.8 μm) calculated for τ_n = (0.1–2) × 10⁻⁹ s, the losses account for 4–6 %.

Recombination losses in the SCR

Recombination of photogenerated charge carriers in the SCR of CdS/CdTe heterostructure can be taken into account using the Hecht equation [54]:

$$ \eta_{\text{H}} (x) = \frac{{\lambda_{\text{n}} }}{W}\left[ {1 - \exp \left( { - \frac{x}{{\lambda_{\text{n}} }}} \right)} \right] + \frac{{\lambda_{\text{p}} }}{W}\left[ {1 - \exp \left( { - \frac{W - x}{{\lambda_{\text{p}} }}} \right)} \right], $$

(19)

where x is the coordinate, where an electron–hole pair arises (x is measured from the front surface of the CdTe layer), and λ_n and λ_p are the drift length of electrons and holes in the SCR, respectively:

$$ \lambda_{\text{n}} = \mu_{\text{n}} F\tau_{\text{no}} , $$

(20)

$$ \lambda_{\text{p}} = \mu_{\text{p}} F\tau_{\text{po}} . $$

(21)

In Eqs. (20) and (21), F is the electric field strength, τ_no and τ_po are the lifetimes of electrons and holes in the SCR, respectively.

In the Schottky diode, an electric field is not uniform, but consideration of the nonuniformity is simplified, since the field strength decreases linearly with the x coordinate. In this case, the field strength F in the expressions (20) and (21) for λ_p and λ_n can be replaced by the mean values of F in the sections (0, x) and (x, W) for electrons and holes, respectively [15]:

$$ F_{(0,x)} = \frac{{(\varphi_{\text{o}} - eV)}}{eW}\left( {2 - \frac{x}{W}} \right), $$

(22)

$$ F_{(x,W)} = \frac{{(\varphi_{\text{o}} - eV)}}{eW}\left( {1 - \frac{x}{W}} \right). $$

(23)

Evidently, charge collection efficiency in the SCR is determined by

$$ \eta_{\text{coll}} = \int\limits_{0}^{W} {\eta_{\text{H}} } (x)\alpha_{\gamma } \exp ( - \alpha_{\gamma } \cdot x)\,{\text{d}}x, $$

(24)

where it is understood that the generation rate of electron–hole pairs in terms of one incident photon is α·exp(−αx) [46].

Figure 13a shows the short-circuit current density J_sc as a function of the width of the SCR, calculated taking into account the recombination losses in the SCR by the formula:

$$ J_{\text{sc}} = q\sum\limits_{i} {\eta_{\text{coll}} (\lambda_{i} )\frac{{T(\lambda_{i} )\Upphi_{i} (\lambda_{i} )}}{{hv_{i} }}} \Updelta \lambda_{i} . $$

(25)

Fig. 13

a Short-circuit current density J_sc taking into account the recombination losses in the SCR as a function of its width W for different carrier lifetimesτ. b Recombination losses, expressed as percentage

When calculating, the lifetimes of charge carriers in the SCR is accepted as earlier to be τ = τ_no = τ_po = 10⁻¹⁰, 5 × 10⁻¹⁰ and 2 × 10⁻⁹ s.

As in the case of recombination at the front surface, the short-circuit current density at W < 0.2–0.3 μm increases with W, because a larger part of the solar radiation is absorbed in the SCR. The J_sc values for different lifetimes at W < 0.2–0.3 μm are the same, because recombination in such a narrow space-charge region does not occurs. When the SCR extends, the J_sc(W) curves calculated for different lifetimes τ diverge. This is due to weakening the electric field leading to inefficient charge collection. When W > 0.5–1 μm, the recombination rate increases so that J_sc begins to decrease (at W > 0.4 μm even at τ = 2 × 10⁻⁹ s). Of course, if one excludes the recombination in the SCR, J_sc for W > 10 μm approaches the maximum possible value 23.2 mA/cm² for the transmission T(λ) of the glass/SnO₂:F/CdS structure.

Figure 13b shows the losses due to recombination in the SCR expressed as percentage. As can be seen, when τ = 10⁻¹⁰ s and the W = 0.8 μm (corresponding to the maximum J_sc) losses are too large (~40 %) and increase even more for greater width of the SCR. In contrast, the recombination losses decrease rapidly with narrowing the SCR and increasing the lifetime of charge carriers. If the SCR is not narrow enough (W > 0.2–0.4 μm) and the lifetime of charge carriers is small (e.g. 10⁻¹⁰ s), unacceptably high losses take place in the CdS/CdTe solar cell due to recombination in the SCR.

Losses due to decrease in the thickness of the CdTe layer and generalization of the results

When considering the recombination at the front surface of the CdTe layer in “Recombination losses at front surface of CdTe layer”, it was established that in trying to create the conditions so that the major part of radiation is absorbed in the SCR, one cannot extend the SCR more than 0.6–0.8 μm giving preference to the largest carrier lifetime τ = 2 × 10⁻⁹ s. As can be seen in Fig. 12a, the maximum in the dependence of J_sc(W) in this case is observed at W = 0.4–0.6 μm, where recombination losses amount to 3–4 %. When SCR width is reduced to 0.3 μm the short-circuit current density J_sc decreases very slightly, but the losses are reduced to 2.4 %. Thus, the width of the SCR W = 0.3 μm can be considered as nearly optimal to minimize losses due to recombination at the front surface of the absorber.

Such a choice of the W value is not contrary to the requirements relating on the recombination losses in the SCR of CdS/CdTe heterojunction. As can be seen from Fig. 13, with a width of the SCR equal to 0.3 μm, the losses due to recombination in the SCR are very low at the carrier lifetimes 2 × 10⁻⁹ s. According to Eq. (5), W = 0.3 μm corresponds to the concentration of uncompensated acceptors close to 10¹⁶ cm⁻³.

An obvious graphic comparison of the recombination losses on the front surface of CdTe and in the SCR is demonstrated in Fig. 14. As can be seen, at W = 0.3 μm the losses due to recombination in the SCR is only ~0.4 %, while at the front surface the loss is ~2.4 %. Thus, the summarized losses due to recombination at the front surface layer and in the SCR with its width of 0.3 μm amount to 2.8 %. The short-circuit current density is reduced due to these losses from 21.3 to 20.7 mA/cm².

Fig. 14

Relative change of J_sc in percent due to recombination at the front surface of the CdTe layer and in the SCR of CdS/CdTe heterojunction

These results were obtained with CdTe layer thickness d = 10 μm. Having fixed the value of W = 0.3 μm and the recombination velocity at the rear surface of the CdTe layer S_b = 10⁷ cm/s let us consider how the J_sc value will change with decreasing the film thickness d. In the following calculations, we will accept the charge carrier lifetime equal to 2 × 10⁻⁹ s (which is a realistic assumption [48–50]) because its shortening leads to a significant reduction of the short-circuit current.

Figure 15 shows the results of such calculations of relative decreasing J_sc (in percentage). As can be seen, the effect of the rear surface recombination on J_sc begins to appear when the thickness of the CdTe layer is less than ~5 μm.

Fig. 15

Effect of the diminishing of photoelectrically active part of the CdTe layer and the optical losses on the short circuit current J_sc (because of insufficient absorptive capacity) as a result of reducing the thickness d of the CdTe layer

Thinning the CdTe layer reduces the current density J_sc primarily, because of the removal of the photocurrent diffusion component which is created outside the space-charge region (d > W). In fact, the electron diffusion length L_n = (τ_n D_n)^1/2 in CdTe with the lifetime τ_n = 2 × 10⁻⁹ s is about 1 μm. So the decrease in CdTe thickness begins to reveal itself, when the thickness d is less than several L_n, i.e. several microns.

Of course, reduction in J_sc further intensifies due to the recombination of charge carriers at the rear surface of the CdTe layer. As can be seen in Fig. 15, reduction in J_sc due to removal of the photocurrent diffusion component and recombination at the rear surface of the absorber layer (labeled as “Photoelectric losses”) amounts to ~5 % at the thickness of the CdTe layer d = 1 μm and increases up to ~12 % at d = 0.5 μm.

It follows from the results presented in “Limitation of efficiency due to insufficient absorptive capacity of the CdTe layer” that at the thicknesses of CdTe less than a few microns the losses associated with the lack of absorptivity A_hv of the CdTe layer reveal themselves perceptibly. Figure 15 shows the reduction of J_sc on the CdTe layer thickness due to a decrease in A_hv taking into account the reflection from the back surface (labeled as “Optical losses”). As it turns out, the reduction of J_sc due to both kinds of losses in the CdTe layer is comparable at d ~ 1.5 μm, but for smaller d the optical losses amount to ~7 % for d = 0.5 μm is lower than the photoelectric losses amounting ~12 % for the same d. We emphasize that “Optical losses” are due to the lack of absorptive capacity of the CdTe layer. As earlier noted, the optical losses due to absorption in the glass substrate, SnO₂:F and CdS layers as well as a reflection on the interfaces taken into account by the factor T(λ_i) in Eq. (9) can be about 16 %.

It is known that to reduce the negative impact of recombination at the rear surface of the CdTe absorber, a heavily doped layer adjacent to the back contact is created. As a result, the potential energy barrier (electron reflector) tends to confine minority carriers in the more lightly doped region. This configuration is equivalent to a cell having a very small recombination velocity S_b at the back surface of the CdTe layer (S_b < 100 cm/s) [46, 48]. Figure 16 illustrates the quantitative effect of recombination on the rear surface of the CdTe layer with changing the film thickness d without electron reflector. The reduction of J_sc is found as the difference between its value at S_b = 10⁷ cm/s and S_b = 0 in Eq. (14).

Fig. 16

The change of the short-circuit current density due to recombination at the rear surface of the CdTe layer as a function of its thickness

As one can see in Fig. 16, if d > 1 μm, the influence of recombination at the rear surface of the CdTe layer increases with decreasing d. This is because the concentration of photogenerated excess electrons Δn increases with decreasing d. In the range d < 1 μm, Δn decreases because Δn = 0 at x = W, which is one of the boundary conditions for solving the continuity equation for the neutral part of the CdTe layer [46]. Note that the maximum losses due to recombination at the rear surface of the CdTe layer do not exceed 4–5 %. At d = 2–3 μm, this kind of losses accounts for ~1 % and only 2–5 % in a narrow range d = 0.5–2 μm. In this regard, the question of reasonability to complicate the technology by creating an electron reflector arises. Obviously, when d ≥ 0.5 μm, the creation of electron reflector makes no sense at all.

Completing the discussion on the dependence of short-circuit current density J_sc on the CdTe layer thickness d, we can summarize the obtained results taking into account all the losses assuming that the width of the space-charge region W is equal to 0.3 μm as its optimum value. Losses due to recombination at the front surface of the CdTe layer and in the SCR can be considered as independent of d and, in accordance with the above discussion, it should be assumed to be 2.4 and 0.4 %, respectively. For losses caused by thinning the absorber layer, one can use the calculation data presented in Fig. 15.

Figure 17 shows the relative change of J_sc as a function of the thickness of the CdTe layer d taking into account all the types of losses discussed above. It follows from the presented data that when d = 2–3 μm (can be considered as typical for the large-scale production of the CdTe modules) the total losses are about 5 % larger than those for a thick layer. When d ≥ 5 μm, the total losses are 3–4 % but while thinning the CdTe layer up to 0.5 μm the losses increase to ~20 %. In absolute values of the short circuit current density J_sc, this corresponds to a decrease of J_sc from 19.7 mA/cm² at d = 2–3 μm to J_sc = 16.6 mA/cm² at d = 0.5 μm.

Fig. 17

Relative change of the short circuit current J_sc depending on the layer thickness d taking into account all types of losses

Evidently, the thinning of the absorber layer up to 0.5 μm reduces the consumption of CdTe, as a material for the manufacture of solar modules, up to 4–6 times compared with those for modules with the thickness of CdTe layer of 2–3 μm. Therefore, one must select “the golden means” to provide the most successful combination of material consumption and efficiency of CdS/CdTe modules.

Thus, the results presented above show in detail how the parameters of the CdTe absorber layer and the CdS window layer affect the characteristics of CdS/CdTe solar cell. Another aspect of the studies is that the comparison of the calculation results with the measured quantum efficiency spectra can quite accurately determine the parameters of solar cells. Among the most important of them are the concentration of uncompensated acceptors and the electron lifetime in the CdTe absorber, as well as the thicknesses of the CdTe and CdS layers. In addition, such a comparison allows formulating the recommendations for corrections of these parameters to increase the efficiency of photoelectric conversion of the device.

Let us demonstrate this by analyzing a fairly typical spectrum of CdS/CdTe solar cell presented in Fig. 18, where the results of measurements and calculations using Eqs. (15)–(18) for various parameters of the CdS/CdTe structure are shown by circles and solid lines, respectively.

Fig. 18

Comparison of the measured spectrum (circles) with the calculations (solid lines) performed for different parameters of CdS/CdTe solar cell

As can be seen in Fig. 18, a good agreement of the calculation results with the measured spectral curve takes place for the concentration of uncompensated acceptors in the CdTe layer N_a − N_d = 6 × 10¹⁵ cm⁻³, the lifetime of electrons in the neutral part of the layer τ_n = 4 × 10⁻¹⁰ s, the thickness of the CdTe layer d_CdTe = 2.5 μm, and the thickness of the CdS film d_CdS = 60 nm. It is also shown in Fig. 18a, b, how the calculated spectrum η(λ) is changed when N_a − N_d and τ_n increase or decrease by one order of magnitude. As seen, such changes of N_a − N_d and τ_n lead to a substantial modification of the spectrum. It should especially be noted that these parameters of the CdTe layer affect the η(λ) spectrum in different ways.

When extending or shortening the electron lifetime τ_n, the quantum efficiency increases or decreases, respectively, only in the λ > 500 nm spectral range (high-energy photons with large absorption coefficient α do not reach the neutral part of the CdTe layer). With a decrease in N_a − N_d (extension of the SCR), the efficiency is improved, but only in the λ > 600 nm range. At λ < 600 nm, the efficiency decreases because recombination on the front surface of the CdTe layer is intensified due to the weakening of the electric field strength. With an increase in N_a − N_d, the rise of η(λ) with increasing λ in the λ = 550–800 nm range is replaced by its decline, i.e. qualitative changes in the spectrum occur. Although in the long-wave part of spectrum, the efficiency decreases with increasing N_a − N_d (narrowing of the SCR), at λ < 500 nm, the intensity of surface recombination reduces and the efficiency increases slightly as a result of the enhanced electric field.

The features of the influence of N_a − N_d and τ_n on the spectral distribution of η(λ) lead to the fact that the best fit of the calculated results with the measured spectrum is achieved only for a single combination of N_a − N_d and τ_n. Note that the deviation of 20–30 % from the selected value of N_a − N_d or τ_n causes noticeable changes in the calculated spectra, i.e. the accuracy of determining these parameters by comparing the calculated and experimental results is quite high.

The data shown in Fig. 18c confirm the expected result that the thinning of the CdS layer leads to a decrease in the efficiency of solar cell only in the λ < 500 nm range, where the fundamental absorption (hv ≥ E_g) takes place in CdS. Finally, as can be seen in Fig. 18d, when thinning the CdTe absorber layer the efficiency η(λ) decreases, but there is almost no change in the λ < 500 nm range since high-energy photons (α > 5 × 10⁵ cm⁻¹) even in a layer of thickness 0.3 μm are almost completely absorbed.

Analyzing only the changes in the quantum efficiency spectra shown in Fig. 18 and neglecting the spectral distribution of solar radiation, one can made too high or too low estimation of the influence of the discussed above parameters on the efficiency of solar cell. More reliable information on the impact of these parameters can be obtained by finding the short-circuit current density J_sc using Eq. (14), which takes into account the spectral distribution of solar radiation. In fact, an increase or decrease of the concentration of uncompensated acceptors N_a − N_d in the CdTe layer by an order of magnitude results in visually comparable changes in the spectrum in Fig. 18a. At the same time, the short-circuit current density J_sc calculated by Eq. (14) increases to 0.6 mA/cm⁻² and decreases to 2.5 mA/cm⁻² at increasing and decreasing N_a − N_d, respectively. This discrepancy is explained by the fact that in the λ = 500–800 nm range, the power of solar radiation significantly decreases with increasing λ and, therefore, increase of η(λ) at λ > 700 nm markedly attenuates. In this sense, the effect of the electron lifetime τ_n is intermediate, since both increase and decrease of τ_n cause more or less uniform change in the η(λ) spectrum and hence similar in magnitude changing of J_sc ≈ ±1 mA/cm⁻².

Thus, the foregoing consideration of the physical processes in CdS/CdTe heterostructure can be used to develop recommendations for the proper optimization of the parameters (purposefully and with sufficient accuracy) for improving the photoelectric conversion efficiency in thin-film CdS/CdTe solar cells.

Conclusions

The results of the calculations performed in this study and their analysis allow us to formulate some important practical conclusions and recommendations concerning the optical and recombination losses in CdS/CdTe thin-film solar cell.

Reflection losses are about 8 % over a wide spectral range, and only in the region λ < 400 nm they increase to 10–11 %. Certainty, reflection losses can be reduced by ~4 % using antireflection coating on the front surface of the glass sheet. Reflection losses in solar cells with ITO and SnO₂:F transparent electrodes differ very little.

Due to absorption in the ITO layer of 200 nm thickness, the short-circuit current J_sc decreases by 12 %; however, the decrease can be 25–26 % when the thickness of ITO layer is 500 nm. In contrast, absorption in the SnO₂:F layer is much lower, causing only a decrease in J_sc of about 2 % at a thickness of 200 nm, and 4–5 % at a thickness of 500 nm. Decrease in J_sc caused by absorption in the CdS layer with a thickness of 50 nm is about 10 % and further increase of 5–6 % occurs at a thickness of 100 nm.

The calculations of absorptivity taking into account the power spectral distribution of the AM 1.5 solar spectrum and the absorption coefficient of CdTe show that in CdTe the total absorptivity (>99.9 %) of photons with energies hv > E_g occurs at a layer thickness more than 20–30 μm. For the CdTe layer thickness of 2–3 μm the absorptivity of photons is about 97 % and reduces to ~93 % at a layer thickness of 1 μm (with no reflection from the rear surface).

Recombination at the front surface of the CdTe layer and in the SCR strongly depends on the width of the space charge region (SCR) W, which is determined by the concentration of uncompensated impurities (defects) in CdTe. The dependence of J_sc on W follows acurve with a maximum at W = 0.4–0.8 μm. The losses due to recombination at the front surface layer and in the SCR with its width of 0.3 μm amount to 2.8 %. When W > 0.3–0.4 μm the recombination losses in the SCR become significant, especially at short lifetimes of charge carriers.

The photoelectric losses outside the SCR caused by thinning the CdTe layer amount to about 1 % if the layer thickness d is 2–3 μm, but increases up to 12–15 %, when d = 0.5 μm. The losses due to lack of absorption capacity for these values of d are 2 and 7 %, respectively. The losses due to recombination at the rear surface of the CdTe layer with no reflection from the rear surface do not exceed 4–5 %.

From the viewpoint of reducing the losses of all types, the width of the SCR of about 0.3 μm is optimal, which corresponds to the concentration of uncompensated acceptors in CdTe close to 10¹⁶ cm⁻³. When the thickness of CdTe layer is 2–3 μm, the total losses are about 5 % greater than in a layer of thickness d > 5 μm. Thinning of the CdTe layer to 0.5 μm decreases J_sc up to ~20 %.

Comparison of the calculation results with the measured quantum efficiency spectra can determine quite accurately the important parameters of solar cells such as the concentration of uncompensated acceptors, the electron lifetime in the CdTe absorber, and the thicknesses of CdTe and CdS layers. Such a comparison allows also formulating the recommendations for corrections of the parameters to increase the efficiency of photoelectric conversion in the device.