Introduction

Despite the abundant nature, solar thermal energy is not being utilized to its full potential, mainly due to mismatch between availability and need. Phase change material (PCM) loaded latent heat thermal storage (LHTS) systems seem to be an attractive solution to this problem. However, all the available PCMs possess very low thermal conductivity, which results in slower rates of charging and discharging. Therefore, thermal conductivity augmentation of PCM is emphasized [1], which is possible through introduction of high conductivity metal particles into the PCMs [2]. When the particles are dispersed into the base fluid (PCM), there would be conductivity enhancement as the particles cluster/aggregate. There is enough evidence in the literature for the significant improvement in the thermal conductivity of PCM even with low particle fraction [3–7].

Khodadadi and Hosseinizadeh [3] have shown that the solidification rate of pure PCM could be increased by adding copper nanoparticles. Ranjbar et al. [4] have also used copper nanoparticles to investigate the solidification of composites in rectangular container and have reported the heat transfer enhancement. However, the experimental results reported by Fan and Khodadadi [5] reveal that the increase in solidification rate is considerable only when the volume fraction of copper oxide particles is 0.5 and further increase in fraction could not accelerate the solidification linearly. The recent work by Kalaiselvam et al. [6] shows that both melting and solidification rates of PCM can be augmented through addition of aluminum/alumina particles. The enhanced heat transfer performance due to the presence of alumina particles in the PCM incorporated in the ceiling of buildings is also reported by Guo [7]. It is clear from the literature review that there has been a growing interest in particle-added PCMs. Nevertheless, only few works are reported. Moreover, only nanosize metal particles, which are very expensive, are considered.

Exergy analysis, based on second law of thermodynamics is an attractive way of evaluating the performance of thermal systems, especially when it comes to optimization [8]. Exergy analysis has been successfully carried out by many researchers for LHTS systems of different applications [9–11]. These studies have proved that the exergy analysis only can provide useful information on valuable energy during charging and discharging processes. When a heat transfer enhancement technique is employed for a LHTS system, the comparison between the systems in terms of exergy performance is more useful. This is because the design of LHTS systems musters a compromise between heat transfer rate, quantity and quality of stored/recovered energy [12]. To the best of authors’ knowledge, the comparison between pure PCM unit and particle-dispersed unit is reported only in terms of thermal performance, except by the previous works of present authors [13, 14].

Our earlier works [13, 14] too have considered only nanosize particles for the thermal performance enhancement of PCMs. At present, the nanoparticles are not economically viable as the cost of nanoparticles is roughly 25 times that of microsize (1 μm = 10−6 m) particles of same material. This is due to mainly the processing cost. However, no work has investigated microsize particle-dispersed PCMs until now. Hence, the primary objective of this work is to examine the role of high conductivity microsize particles in augmenting the heat transfer performance of pure PCM as well as the exergy performance of the storage system. To the best of our knowledge, this is a maiden attempt investigating the cheaper form (microsize) of conductivity particles. Since microparticles are used in the present work as against the nanoparticles considered in our earlier works [13, 14], the methodology of investigation differs completely. Firstly, the thermo-physical properties of microparticles–PCM composites are evaluated experimentally as the analytical procedure employed in earlier works [13, 14] is valid for only nanoparticles–PCM composites. Secondly, the numerical modeling technique adopted here is quite different from that one used for nanoparticles system. This is because the formulation needs to take into account the migration of such microsize particles due to non-uniform shear fields in the liquid which is not the case when it comes to nanoparticles. Because of the expected particle migration, the present formulation also includes the momentum equation which of course is not considered for nanoparticle composites. As the particles are expected to continue migrating all the time, the present work aims at investigating the consequences of particle migration from performance enhancement point of view. This work is also intended to compare the relative benefits/shortcomings of microparticles dispersion in comparison with nanoparticles dispersion. The comparison is also extended to positive and adverse effects of particles dispersion on the exergy performance of conventional PCM.

Preparation and characterization of PCM–microparticles composites

Among the high conductivity particles like silver, nickel, gold, alumina, copper, aluminum etc., copper and aluminum are less expensive and easily available. As far as cost is concerned, there is not much difference between copper and aluminum. However, the thermal conductivity of copper is significantly higher than that of aluminum. The microcopper particles were prepared out of copper rods (99.9 % purity) using simple filing technique. Although it was difficult to control the size of the particles and size uniformity by manual filing, a smoothest file was used to obtain particles of smallest possible size. The size of the prepared particles was measured with electron microscope and the average size was found to be 250 μm. Prior to dispersing the copper particles (99.9 % purity), the same were coated with a surfactant, to enhance the stability of suspended particles. The PCM considered in this work is a hydrated salt and if the base fluid is such a polar solvent, ionic surfactants which are water soluble are generally recommended [15]. In view of this and availability, sodium acetate was chosen as a surfactant. The ratio of copper particles to the surfactant was 3:1 by mass. The surfactant-coated copper particles were then, dispersed into the liquid PCM (Product of Pluss Polymers, India-http://www.thermalstorage.in/plussproducts.html). The PCM (HS58) is a mixture of hydrated salts, additives and nucleating agents. Table 1 presents the properties of the PCM. Throughout the preparation, the PCM was kept at a temperature sufficiently higher than its melting point. A thermostat controlled electric heater was used to heat the mixing container.

Table 1 Thermo-physical properties of HS-58
Full size table

While dispersing the particles, the liquid PCM in the mixing container was thoroughly stirred for about 15 min using a magnetic stirrer. After the stirring process, the mixture was treated with ultrasonic disruptor for more than 1 h. The amplitude and frequency of ultrasonic waves were set as 50 % and 50 Hz, respectively, during the sonication.

Measurement of latent heat and specific heats

For the measurement of thermo-physical properties of PCM, the most commonly used methods are drop calorimetry (DC), differential thermal analysis (DTA) and differential scanning calorimetry (DSC) methods. However, these methods are known for various shortcomings. They are,

  • The sample PCM to be tested should be of very small size (1–10 mg). However, the properties of bulk PCM would be different from those of sample. Especially, when it comes to PCM composites, the heterogeneous of additives cannot be accounted for, if the sample size is very small. Moreover, the small sample size cannot reflect the degree of supercooling of the PCM as the small container would show higher degree of supercooling.

  • Due to the small sample size, the phase change process cannot be visualized. Especially, the volume expansion of liquid PCM, which is critical for the computation of effective thermal conductivity during melting, cannot be observed.

  • The related experimental units are complicated and expensive.

  • These methods cannot measure the properties of several samples simultaneously.

  • Thermal conductivity values cannot be obtained.

In view of the above-mentioned facts, the present work employs, a simple and cost effective method, namely Temperature–History method developed by Yinping et al. [16] for the measurement of all the thermo-physical properties. The liquid PCM, which is at a higher temperature than its melting point (Tinit < Tm), in a test tube is suddenly exposed to atmosphere which allows the freezing of liquid PCM. The measurement of temperature of PCM at every small time interval would enable plotting the T-History curve. Typical T-History plots with three divided regions are shown in Fig. 1a, b.

Fig. 1
figure 1

T-History curves of a PCM—without supercooling b PCM—with supercooling c reference fluid

Full size image

The cooling of PCM can be termed as a conduction problem that involves surface convection effects. Hence, the Biot number (Bi = hR/2 k, where h is the heat transfer coefficient of air outside the tube, R is the radius of tube and k is the thermal conductivity of PCM) plays an important role. In such problems, if the condition of Bi < 0.1 is satisfied, then the temperature distribution can be assumed as uniform and it allows employing the lumped capacitance method. In view of this, the tube of very smaller diameter as compared to the length has been chosen in the work (i.e. inner diameter = 13 mm, length = 155 mm). These dimensions along with surrounding atmosphere would keep Bi lower and hence, error associated with the employment of lumped capacitance method would be negligible.

When lumped capacitance method is applicable, the energy balance equations for liquid sensible cooling (t0 ≤ t ≤ t1), phase change (t0 ≤ t ≤ t1) and solid sensible cooling (t2 ≤ t ≤ t3) periods are given, respectively,

$$ \left( {m_{\text{t,p}} c_{\text{p,t}} + m_{\text{PCM}} c_{\text{p,l}} } \right)\,\left( {T_{\text{init}} - T_{\text{s}} } \right) = hA_{\text{t}} A_{1} $$
(1)
$$ \left( {m_{\text{t,p}} c_{\text{p,t}} + m_{\text{PCM}} \left( {\frac{{c_{\text{p,l}} + c_{\text{p,s}} }}{2}} \right)} \right)\left( {T_{\text{m}} - T_{i} } \right) + m_{\text{PCM}} \lambda = hA_{\text{t}} A_{2} $$
(2)
$$ \left( {m_{\text{t,p}} c_{\text{p,t}} + m_{\text{PCM}} c_{\text{p,s}} } \right)\,\left( {T_{i} - T_{\text{f}} } \right) = hA_{\text{t}} A_{3} $$
(3)

Along with PCM, another tube containing distilled water (reference fluid) at the same temperature of PCM is also exposed to the same atmosphere and T-History curve is shown in Fig. 1c. This curve can also be divided into three portions using the same temperature ranges used for PCM and the energy equations are,

$$ \left( {m_{\text{t,w}} c_{\text{p,t}} + m_{\text{w}} c_{\text{p,w}} } \right)\,\left( {T_{\text{init}} - T_{\text{s}} } \right) = hA_{\text{t}} 'A_{1} ',t_{0} ' \le t \le t_{2} ' $$
(4)
$$ \left( {m_{\text{t,w}} c_{\text{p,t}} + m_{\text{w}} c_{\text{p,w}} } \right)\,\left( {T_{\text{m}} - T_{i} } \right) = hA_{\text{t}} 'A_{2} ',t_{1} ' \le t \le t_{3} ' $$
(5)
$$ \left( {m_{\text{t,w}} c_{\text{p,t}} + m_{\text{w}} c_{\text{p,w}} } \right)\,\left( {T_{i} - T_{\text{f}} } \right) = hA_{\text{t}} 'A_{3} ',t_{3} ' \le t \le t_{4} ' $$
(6)

Finally, simple mathematical manipulation of Eqs. (1) through (6) results in expressions for liquid and solid specific heat and latent heat of PCM. They are,

$$ c_{\text{p,l}} = \frac{{m_{\text{t,w}} c_{\text{p,t}} + m_{w} c_{\text{p,w}} }}{{m_{\text{PCM}} }}\frac{{A_{\text{t}} }}{{A_{\text{t}} '}}\frac{{A_{1} }}{{A_{1} '}} - \frac{{m_{\text{t,p}} }}{{m_{\text{PCM}} }}c_{\text{p,t}} $$
(7)
$$ c_{\text{p,s}} = \frac{{m_{\text{t,w}} c_{\text{p,t}} + m_{\text{w}} c_{\text{p,w}} }}{{m_{\text{PCM}} }}\frac{{A_{\text{t}} }}{{A_{\text{t}} '}}\frac{{A_{3} }}{{A_{3} '}} - \frac{{m_{\text{t,p}} }}{{m_{\text{PCM}} }}c_{\text{p,t}} $$
(8)
$$ \lambda = \frac{{m_{\text{t,w}} c_{\text{p,t}} + m_{\text{w}} c_{\text{p,w}} }}{{m_{\text{PCM}} }}\frac{{A_{\text{t}} }}{{A_{\text{t}} '}}\frac{{A_{2} }}{{A_{2} '}}\left( {T_{\text{m}} - T_{i} } \right) - \left( {\frac{{m_{\text{t,p}} }}{{m_{\text{PCM}} }}c_{\text{p,t}} + \left( {\frac{{c_{\text{p,l}} + c_{\text{p,s}} }}{2}} \right)} \right)\left( {T_{\text{m}} - T_{i} } \right) $$
(9)

It should be noted that the selection of t1 is straight forward as the release temperature (Ts) is starting point of solidification. However, it would be difficult to locate the end point of solidification as solidification may not take place isothermally. This problem is not addressed by Yinping et al. [16]. Hence, the present work adopts a new technique i.e. use of inflection point to indicate the end of solidification process. The inflection point is the one at which the first derivative of T-History curve becomes minimum [17]. This can be justified by the fact that the temperature of PCM remains constant or decreases gradually during phase change, but decreases exponentially once the phase change is completed.

Measurement of thermal conductivities

If the test tube containing molten PCM is suddenly put into the water, which is at a temperature lower than the melting temperature of PCM, solidification can be initiated. Because of smaller diameter to height ratio, the lumped capacitance method is applicable here also. Hence, the heat transfer from PCM to water during solidification is one dimensional and the one dimensional transient heat diffusion equation for cylindrical geometry can be written as,

$$\frac{k_{s}} {\rho c_{\text{p,s}}} \frac{1} {r} \frac{\partial} {\partial r} \left(r {\frac{\partial T}{\partial r}} \right) = \frac{\partial T} {\partial t} \quad {r_{\text{int}} \le r \le r_{i} ,\quad t > 0} $$
(10)

The initial and boundary conditions are, respectively,

$$ \begin{gathered} \left. {k_{\text{s}} \frac{\partial T}{\partial r}} \right|_{{r = r_{i} }} \quad = h_{\text{w}} \left( {T_{\text{w}} - T\left( {r_{{_{i} }} ,t} \right)} \right)\quad t > 0 \hfill \\ T\left( {r_{\text{int}} = r_{i} } \right) = T_{\text{m}} \quad t = 0 \hfill \\ \end{gathered} $$

At all instants, the conditions for solid/liquid interface are,

$$ \begin{array}{*{20}c} {r_{\text{int}} = r_{i} } & {t = 0} \\ \end{array} $$
$$ \left. {\frac{{k_{\text{s}} }}{{\rho_{\text{s}} \lambda }}\frac{\partial T}{\partial r}} \right|_{{r = r_{\text{int}} }} = \frac{{\partial r_{\text{int}} }}{\partial t} $$

Now Eq. (10) along with initial and boundary conditions can be solved using perturbation method. The solution procedure of perturbation method can be found elsewhere [18]. Accordingly, the resulting equation for thermal conductivity of solid PCM is given as,

$$ k_{\text{s}} = \frac{{\left[ {1 + {\text{Ste}}} \right]}}{{4\left[ {\frac{{t_{\text{f}} \left( {T_{\text{m}} - T_{\text{w}} } \right)}}{{\rho_{\text{s}} r_{i}^{2} \lambda }} - \frac{1}{{h_{\text{w}} r_{i} }}} \right]}} $$
(11a)

where tf is the time taken for complete solidification.

The above equation can further be simplified by neglecting the term, \( \frac{1}{{h_{\text{w}} r_{i} }} \) as Yinping et al. [16] have stated that,

$$ \frac{{t_{\text{f}} \left( {T_{\text{m}} - T_{\text{w}} } \right)}}{{\rho_{\text{s}} r_{i}^{2} \lambda }} \gg \frac{1}{{h_{\text{w}} r_{i} }} $$

Thus, we have,

$$ k_{\text{s}} = \frac{{\left[ {1 + {\text{Ste}}} \right]}}{{4\left[ {\frac{{t_{\text{f}} \left( {T_{\text{m}} - T_{\text{w}} } \right)}}{{\rho_{\text{s}} r_{i}^{2} \lambda }}} \right]}} $$
(11b)

Similarly, the tube containing solid PCM is dipped into a hot water bath, which is at a temperature higher than the melting point of PCM. Once the time taken for the complete melting (tm) is known, the expression for thermal conductivity of liquid PCM can be arrived following a similar procedure described above.

$$ k_{\text{l}} = \frac{{\left[ {1 + {\text{Ste}}} \right]}}{{4\left[ {\frac{{t_{\text{m}} \left( {T_{\text{w}} - T_{\text{m}} } \right)}}{{\rho_{\text{l}} r_{i}^{2} \lambda }}} \right]}} $$
(12)

In fact, Eqs. (11a, 11b) and (12) are obtained by neglecting second order term of the perturbation expansion. However, the error in the calculated values would be less significant i.e. <5 %, if the following conditions are satisfied.

  • Bi <0.1—This is to ensure the one dimensional heat transfer

  • Ste <0.5—Ste is taken as the smaller perturbation parameter in the perturbation method and the variables (temperature, interface location and time) are expanded as powers in terms of Ste

Mathematical formulation

In order to investigate the melting and solidification heat transfer characteristics of microparticles–PCM composites, a two dimensional shell and tube module is employed. The PCM is stored in the insulated shell and the tube carries heat transfer fluid (HTF). The vertical orientation of unit is considered to ensure the axisymmetric phase change around the inner tube and thus, only one half of the physical model with axis as symmetry line is sufficient for computational analysis (Fig. 2). All the physical boundaries along with the axis are adiabatic boundaries. In all numerical trails, the dimensions of the unit were kept constant and are given in Table 2.

Fig. 2
figure 2

Computational model of LHTS unit

Full size image
Table 2 Dimensions of system
Full size table

As mentioned earlier, migration of microsize particles is generally observed due to non-uniform shear fields in the liquid. This means that the particles migrate from higher shear rate regions to lower shear rate regions. Hence, it becomes necessary to track the spatial variation of particle concentration at all times during the phase change processes. To evaluate particle concentration, this work incorporates a constitutive equation which is proposed by Phillips et al. [19]. The constitutive equation is obviously a transport equation for particle flux and is given as,

$$ {\frac{\partial e}{\partial t} + u.\nabla e = \nabla .\left[ {a^{2} e\dot{\gamma }\left( {K_{c} + K_{\mu } e\frac{1}{\mu }\frac{\partial \mu }{\partial e}} \right)\nabla e} \right]} + K_{c} a^{2} e^{2} \nabla \dot{\gamma } $$
(13)

The first term on the right hand side of Eq. (13) is the diffusive term with diffusive coefficient \( \Upgamma = a^{2} e\dot{\gamma }\left( {K_{c} + K_{\mu } e\frac{1}{\mu }\frac{\partial \mu }{\partial e}} \right) \) and the second term on the right hand side of Eq. (13) is nothing but source term (Se).

Following the continuum approach, the conservative equations for mass and momentum are written as,

$$ {\frac{\partial \rho }{\partial t} + \nabla .(\rho V) = 0} $$
(14)
$$ {\frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{\partial p}{{\partial x_{i} }} + \mu \frac{{\partial^{2} u_{i} }}{{\partial x_{{_{j} }}^{2} }}} + \Updelta \rho .g + S_{i} $$
(15)

The source term of Eq. (15) is buoyancy term which describes natural convection through density as a function of temperature. However, the Boussinesq model of natural convection defines density as a constant value irrespective of temperature in all equations except for the buoyancy term in the momentum equation as given below.

$$ \Updelta \rho .g = \rho \beta (T - T_{ 0} )g $$
(16)

Hence, the momentum equation becomes,

$$ {\frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{\partial p}{{\partial x_{i} }} + \mu \frac{{\partial^{2} u_{i} }}{{\partial x_{{_{j} }}^{2} }}} + \rho \beta (T - T_{ 0} )g + S_{i} $$
(17)

The momentum equation of PCM is largely affected by the dispersion of particles as the particles addition changes the rheological behavior of the pure PCM. Hence, the viscosity needs to be defined as a function of particle fraction and Krieger equation [20] is applicable for the same.

$$ \mu_{\text{eff}} = \mu \left( {1 - \frac{e}{{e_{\hbox{Max} } }}} \right)^{ - 1.82} $$
(18)

where emax is the particle fraction when the effective viscosity tends to infinity and is 0.68 for hard spherical particles.

The source term in momentum equation allows the formulation to treat the solid and liquid phases of PCM as porous media and is given as,

$$ S_{i} = - Au_{i} $$
(19)

In a computational cell, the velocity of liquid has a finite value and becomes zero when cell is full of solid. This can be formulated by defining the coefficient A as a function of liquid fraction of the computational cell. i.e.,

$$ A(f_{\text{l}} ) = \frac{{C\left( {1 - f_{\text{l}} } \right)^{2} }}{{f_{\text{l}}^{3} + \varepsilon }} $$
(20)

The constant C is called ‘mushy zone constant’ and is set as 10,000. The other constant ϵ is a small computational constant taken as 0.001 to avoid division by zero arising from zero liquid fraction.

Now the energy equation is,

$$ {\frac{\partial }{\partial t}\left( {\rho h} \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} h} \right) = \frac{\partial }{{\partial x_{i} }}\left( {k\frac{\partial T}{{\partial x_{i} }}} \right)} $$
(21)

For HTF, the following mass, momentum and energy conservative equations.

$$ {\frac{\partial \rho }{\partial t} + \nabla .(\rho V) = 0} $$
(22)
$$ {\frac{\partial (\rho V)}{\partial t} + \nabla .(\rho VV) = - \nabla P + \mu \nabla^{2} }V + \rho g $$
(23)
$$ {\frac{\partial T}{\partial t} + V\nabla T = \alpha \left( {\nabla^{2} T} \right)} $$
(24)

The numerical model considers only laminar flow of HTF as turbulent does not have any role in enhancing the phase change rate [13, 14].

For numerical solution of governing equations, the commercial computational fluid dynamics (CFD) code called FLUENT 6.2.36 is adopted. The code uses an iterative procedure in which the phase change rate is linearized as truncated Taylor series and then the old iteration values are used to compute the linear term. The mesh is created using quadrilateral elements and numerical trials involving pure PCM were performed with coarse and finer meshes, i.e. grid spacing ranging from 0.1 to 0.001. From the results of instantaneous heat fluxes and liquid fraction (Table 3), the grid spacing of 0.0015 seems to be the optimum one as further decrease does not result in any notable differences in the results.

Table 3 Instantaneous heat flux and liquid fraction values with various grid sizes (Pure PCM, Tin = 340 K)
Full size table

Time step size of 0.001 s was selected for transient analysis as increase in time step led to convergence difficulties and decrease could not make any difference in the results. The difference between liquid fraction values obtained with time step size of 0.001 and that of obtained with 0.0005 was found to be in the range of 0.1–0.2 %.

For the convergence of the solution, convergence criterion of 10−5 for continuity and momentum equations and 10−6 for energy equations were fixed. To improve the rate of convergence, under relaxation factor was introduced and the optimum under relaxation factor for liquid fraction update was found to be 0.7. The solution controls used are:

  • SIMPLE algorithm for pressure–velocity coupling

  • Standard scheme (pressure equation) and Second order upwind scheme (momentum and energy equations) as discretization schemes

In Fluent solver, unique modeling requirements can be dynamically loaded in the form of separately developed codes written in “C” language. This sort of code is called user defined function (UDF). Hence, a UDF was developed to take into account the variation of thermal conductivity with respect to two solution variables, i.e. temperature and particle fraction, and the same was compiled in the solver. Similarly, another UDF which defines the particle fraction-dependent viscosity was compiled.

The major difference between modeling of nano and microparticles systems lies in the form of particle flux equation which is a customized equation. In the solver, only standard conservative equations are preloaded and thus, the solver considers the particle flux equation as an additional transport equation for an arbitrary scalar. Hence, the particle flux has to be defined as a scalar which is called user defined scalar (UDS). Similar to UDF, UDS has to be executed in the form of a separate code written in “C” language. For the execution of UDS, two UDFs were also required as they define the diffusion coefficient and source term of particle flux equation.

Exergy analysis

Following the authors’ previous works [13, 14], the exergy parameters are computed as follows:

Charging process

Rate of exergy transferred by HTF,

$$ {\dot{\text{E}}\text{x}}_{\text{HTF}} = {\dot{m}}c_{{\text{p}},{\text{HTF}} } \left[ {\left( {T_{\text{in}} - T_{\text{out}} } \right) - T_{\text{atm}} \ln \left( {\frac{{T_{\text{in}} }}{{T_{\text{out}} }}} \right)} \right] $$
(25)

Rate of exergy stored,

$$ {\dot{\text{E}}}{\text{x}}_{\text{PCM}} = {\dot{Q}}\left[ 1-\frac{T_{\text{atm} }}{T_{\text{PCM}}} \right] $$
(26)

Exergy efficiency,

$$ \psi = \frac{{\dot{E}x_{\text{PCM}} }}{{\dot{E}x_{\text{HTF}} }} $$
(27)

Discharging process

Rate of exergy transferred by PCM,

$$ {\dot{E}x_{\text{PCM}} = - \dot{Q}}\left[ {1 - \frac{{T_{\text{atm}} }}{{T_{\text{PCM}} }}} \right] $$
(28)

Rate of exergy recovered,

$$ {\dot{E}}x_{\text{HTF}} = {\dot{m}}c_{{{\text{p}},{\text{HTF}} }} \left[ {\left( {T_{\text{out}} - T_{\text{in}} } \right) - T_{\text{atm}} \ln \left( {\frac{{T_{\text{out}} }}{{T_{\text{in}} }}} \right)} \right] $$
(29)

Exergy efficiency,

$$ \psi = \frac{{\dot{E}}x_{\text{HTF}}}{{\dot{E}}x_{\text{PCM}} } $$
(30)

Experimental set up

An experimental test rig was built in-house to verify the accuracy of the numerical model (Fig. 3). The main test section comprises two co-axial cylindrical tubes. The outer acrylic tube (9 cm inner diameter and 10 cm outer diameter) is having sealed bottom cover and removal top cover. The removal cover facilitates the easy filling and removal of PCM. Moreover, the unsealed top cover allows the air to escape during melting of PCM. The inner tube made of copper (diameter 1.9 cm and thickness 0.1 cm) allows the hot/cold water to flow downwards. The annular space between the inner and outer tubes serves as storage compartment for PCM–particle composites. The effective height of test section is 10 cm. The entire test section including the top and bottom surfaces was covered with glass wool insulating material.

Fig. 3
figure 3

Schematic of experimental setup

Full size image

A water bath located above the test section was used to supply water at constant temperature with an accuracy of ±2 °C. For flow rate measurements, a rotameter (accuracy (±3 %) was used. During the experiments, temperatures of PCM were measured at different radial and axial locations. Nine k-type thermocouples calibrated with accuracy of ±1.5 % were inserted at radial positions 0.5, 3 and 4 cm from centre of the test section and at axial positions 3, 6 and 9 cm from the top. Because of axisymmetric phase change processes, all thermocouples are placed only on the right side of PCM. In addition, two thermocouples were used to measure the inlet and outlet temperatures of water to confirm the change in temperature of water during charging and discharging.

Results and discussions

Validation of the numerical model

Figure 4 presents the comparison between numerical and experimental results for representative locations. As seen, certain discrepancy between numerical and experimental results is observed and the deviation of numerical results from experimental measurements is relatively higher during melting.

Fig. 4
figure 4

Comparison of results of numerical model employed with those of experiments

Full size image

As it is discussed in the later part of this section, the composite PCMs suffer from uneven distribution of particles due to particle migration from one region to other regions. The non-uniform distribution of particles calls for definition of thermal properties as functions of the variable, i.e. particle fraction. However, the CFD code used in this work permits only definition of thermal conductivity as a variable and the specific heat and latent heat values are to be defined as constants. This limitation results in some difference between numerical and experimental results. Since the particle migration is found to be prevailing only during melting process, the definition of constant specific heat and latent heat could not affect the solidification results. Similarly, the effect of particle migration is stronger in composites of lower particle fraction and thus, the deviation of numerical results from experimental measurements is more pronounced in case of composites with 0.1 particle fraction. In general, the deviation increases as the time progresses due to stronger particle migration at later stages of melting.

In case of solidification, discrepancy arises due to mainly the difficulty in maintaining the adiabatic wall conditions and variation of temperature of HTF at the inlet during experimentation. Experimental uncertainties have also contributed to a certain extent. Despite the deficiency, the predicted values are qualitatively correct and the results confirm the validity of the adopted numerical model.

Thermo-physical properties

For each composite, the T-History experiments were performed twice with different initial temperatures (around 10 and 30 °C above the melting point) to verify the accuracy of measurements. In general, the difference between two set of results was not more than 3 %. Similarly, to check the repeatability of measurements, the trial for any sample was conducted twice and it was found that each result differs from corresponding result of repeated trial only by <1 % (Table 4).

Table 4 Experimentally evaluated properties of microparticles composites
Full size table

In order to establish a relationship between thermal conductivity and particle fraction, Fig. 5 is plotted. In the plot, symbols represent the experimental results of thermal conductivity and the curve is the generated linear regression corresponding to the experimental data. The curve fitting procedure subsequently led to the following function, which was used in the UDF of thermal conductivity.

Fig. 5
figure 5

Variation of thermal conductivity of liquid microparticles composites with particle fraction

Full size image
$$ k_{\text{l}} = 0.39686 + 1.57022e $$

Performance of LHTS unit employing PCM–microparticles

The heat transfer and exergy performances of microparticle-dispersed systems are presented in comparison with those of nanoparticle-dispersed systems. The nanoparticles composites were analyzed employing the numerical procedure reported in our earlier papers [13, 14]. Due to the enhanced thermal conductivity by microparticles, it is obvious that the heat transfer rate is much higher throughout the solidification process (Fig. 6a). However, it is also important to examine the relative strength of microparticles in enhancing the heat transfer rate.

Fig. 6
figure 6

Effect of microparticles on instantaneous heat transfer rate during solidification a for various particle fractions b in comparison with effects of nanoparticles

Full size image

According to Table 5, the microparticles composite of any particle fraction shows relatively higher increase in thermal conductivity as compared to nanoparticles composite of same particle fraction. Due to relatively larger size, microparticles can remain closer to each other than what is possible in nanoparticles composites. This means the particles network is stronger in microparticles composites than in their counter parts. However, it is known that the particles migration in microparticles composites leads to non-uniform distribution of particles. Thus, the heat transfer rate may be higher only at locations where more particles exist and there may not be much enhancement in the overall heat transfer rate. Moreover, as the particle fraction at any location may vary with time, the qualitative behavior of microparticles composites in terms of heat transfer rate may not be same as that of nanoparticles composites.

Table 5 Increase in thermal conductivity of pure PCM due to particles
Full size table

The comparison of nano and microparticles in terms of heat transfer rate enhancement is shown in Fig. 6b. Accordingly, the enhancement in the heat transfer rate due to microparticles dispersion is relatively higher than that of nanoparticles dispersion and this is true for any value of particle fraction. Moreover, microparticle composites maintain higher heat transfer rates at all times throughout solidification. This clears that there is no difference between microparticles and nanoparticle systems from qualitative perspective, although the enhancement by the former is quantitatively higher than that by the latter.

The higher heat transfer rate at all times highlights that the initial particle fraction, which is uniform everywhere remains same throughout the solidification. This can be verified from Fig. 7a–c, in which the time variation of particles fraction is shown. As it can be seen, the variation of particle fraction with time is negligible. Same is observed at all locations. Hence, the particle migration appears to be very weak during solidification. The reason for the insignificant particle migration is simple and straight forward. The onset of particle migration is mainly due to strain rate gradient and the strain rate gradient depends on the strength of fluid flow. During phase change, the only fluid flow is due to natural convection which is incomparable during solidification [1]. Obviously, the weaker fluid flow could not promote the particle migration and thus, microparticles exhibit higher solidification rates at all times as compared to their nano-counterparts.

Fig. 7
figure 7

Time variation of particle fraction (a–c) during solidification (d–f) during melting

Full size image

In order to quantify the relative benefit of microparticles over nanoparticles, the decrease in solidification times due to microparticles is compared with that of due to nano particles. The results are presented in Table 6 and provide further evidence to the superiority of microparticles during solidification.

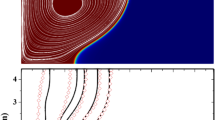
Table 6 Decrease in complete solidification time due to nano and microparticles addition (Tin = 283 K)
Full size table

Unlike solidification, the flow of liquid PCM cannot be ignored during melting due to the existence of natural convection. Hence, to examine the particle distribution at various times during melting, the concentration profiles are plotted along the radial direction (Fig. 7d–f). Since composites of various particle fractions melt at different rates, in view of comparison, the presented profiles are the one those correspond to melt fractions 0.25, 0.5 and 0.75.

In the liquid region, the distribution of particles is such that the volume fraction is found to be the lowest, adjacent to the tube wall, and gradually increases in the radial direction. The increase in volume fraction continues up to the middle of the liquid region and thereafter the value starts decreasing to reach the minimum value at the liquid–solid interface. As it is known, the fluid flow due to natural convection is established as simultaneous upward and downward motions of liquid with the former along the tube wall and the latter along the interface. In such case, it can be assumed that the upward motion is bounded by the left half of the liquid region where as the downward motion exists within the second half. For the upward motion of hot fluid, the local shear rate at tube wall remains maximum and the maximum shear rate forces the particles moving to the centre region where the shear rate is zero. Similarly, maximum shear rate should be found at the interface as it acts as a wall. Hence, the particles are forced to migrate toward centre region due to the flow of cold liquid. This is the reason why the particle profiles appear as shown in Fig. 7d–f.

Although the above-mentioned trend is observed for all values of particle fractions, the variation along the radius becomes less as the particle fraction increases. This can be attributed to the fact that higher particle fraction weakens the natural convection, which in turn dampens the particle migration. The observed particle migration in this work is consistent with the results of Phillips et al. [18]. As the melting progresses, natural convection becomes stronger and hence, the particle migration would be on increasing mode. As a result, steeper particle concentration profiles are observed at later stages of melting.

The time variation of heat transfer rates during melting of microcomposites is compared with that of pure PCM in Fig. 8a. In general, heat transfer enhancement due to microparticles in the PCM is observed only for some initial period of melting. No enhancement but rather decreased heat transfer rate could be seen during the remaining period. In fact, enhanced heat transfer in the beginning and decreased heat transfer later are found also with nanoparticles composites. Hence, both the versions of particles enhance the heat transfer only during the conduction dominated period.

Fig. 8
figure 8

Effect of microparticles on instantaneous heat transfer rate during melting a for various particle fraction b in comparison with effects of nanoparticles

Full size image

Since microparticles addition dampens the natural convection considerably, convection dominated melting becomes slow. However, there is significant difference between nanoparticles composites and microparticles composites as shown in Fig. 8b. First notable difference lies in the form of heat transfer enhancement period. Overall, microparticles of any fraction enhance the heat transfer rate for shorter period in comparison with its nano-counterpart. However, the gap narrows down with increase in particle fraction. Due to higher thermal conductivity, microparticles PCMs are supposed to exhibit higher heat transfer rate for longer period as compared to nanoparticles PCMs. However, due to particle migration in the liquid PCM, particle fraction adjacent to heat transfer surface becomes less and keeps reducing as time progresses. Hence, effective thermal conductivity may not be considerably high so that the reduction in heat transfer owing to dampened natural convection could be compensated. As seen earlier, particle migration is not significant when particle fraction is higher and thus, higher particle fraction composites could exhibit higher heat transfer rate for longer period. Because of same reason, during enhanced heat transfer period, there is not much difference between the heat transfer rates of nano and microcomposites of lower particle fractions. The difference widens as the particle fraction increases. Nevertheless, relatively higher heat transfer rates are observed with microparticles PCMs of any fraction in comparison with nanoparticles composites of same volume fraction.

During convection-dominated period, both the types of composites show poor heat transfer rates as compared to pure PCM and microparticles composites seem to be suffering more irrespective of volume fraction. This is due to the combined effect of higher viscosity and particle migration. In case of nanoparticles PCMs, first of all there is no particle migration and thus, the effective thermal conductivity remains uniform, which in turn compensates the effect of dampened natural convection to a certain extent. On the other hand, significant particle migration is observed with microparticles of all particles fractions especially at higher times. The particle migration, as it is known, cannot help in enhancing the conduction heat transfer rate. Moreover, microparticles PCM of any particle fraction is more viscous than its nano-counter parts (Table 7). The higher viscosity obviously has a significant role in reducing the convection heat transfer.

Table 7 Comparison of viscosities of nano and microparticles composites
Full size table

Despite lower heat transfer rates during convection-dominated period, microparticles composite of any particle fraction needs less time for complete melting as compared to nanoparticle composite of same particle fraction/pure PCM. Higher melting achieved during conduction dominated period helps the microcomposites to dominate nanocomposites and pure PCM throughout the melting process and the effect of lower heat transfer rate is not pronounced in this regard. The comparison of micro and nanocomposites in terms of reduction in melting time is given in Table 8. It should be mentioned that the superiority of microparticles composites in reducing the melting time is more pronounced if the particle fraction is higher. Again this is related to particle migration. As seen earlier, higher heat transfer rates are observed for longer period when particle fraction is more because of weak particle migration. Lower heat transfer rate for a smaller period could not dampen the effect of high heat transfer rate, which prevails for longer period. As a result, higher particle fraction microcomposites are found to be reducing melting time significantly. On the other hand, only moderate reduction is observed when particle fraction is less as the effect of enhanced melting rate is dampened to a certain extent by lower rate of heat transfer during long period of melting.

Table 8 Decrease in complete melting time due to nano and microparticles addition (Tin = 350 K)
Full size table

As it is seen, both nano and microparticles enhance the solidification rate of pure PCM significantly. Similarly, the heat transfer between PCM and HTF takes place at higher temperatures when particles are dispersed. Therefore, the exergy efficiency of particles dispersed PCMs should be higher than that of pure PCM. Moreover, the solidification rates and temperatures at which heat transfer occurs are found to be better with microparticles and thus, it can be predicted that systems with microparticles–PCM composites could exhibit higher exergy efficiency than those of their nanoparticle counter parts. The exergy efficiency results displayed in Fig. 9a back the points discussed above.

Fig. 9
figure 9

Comparison of effects of nano and microparticles on exergy efficiency a during solidification b during melting

Full size image

During melting, microcomposites possess better exergy efficiency than nanocomposites or pure PCM only when the heat transfer rate is enhanced as shown in Fig. 9b. During this period, the difference between exergy efficiencies of micro and nanocomposites is more significant, if the particle fraction is higher. This is because of large gap between the heat transfer rates of those two composites. Similar behavior in terms of difference in exergy efficiencies can be seen even during the second part of melting, i.e. the period of decreased heat transfer rate by nano/microcomposites. However, now the exergy efficiency of the microcomposites is less in comparison with nanocomposites or pure PCM as the former is found to be inferior in terms of heat transfer rate during this period.

The reduction of latent heat of pure PCM is more pronounced when microparticles are added. Due to this fact, the ratio of total energy recovered from microparticle-added PCM and that from pure PCM is significantly less as compared to the ratio obtained from nanoparticles as seen from Fig. 10a. However, the microparticles appear to be superior over nanoparticles, if the comparison is made in terms of ratio of total exergy recovered from composites and that from pure PCM (Fig. 10a). The superior exergy performance by microparticles composites is again attributed to the combined effect of higher heat transfer rates and lesser solidification time.

Fig. 10
figure 10

Comparison of effects of nano and microparticles on a total energy recovered/total exergy recovered b total energy stored/total exergy stored

Full size image

As observed during solidification, the effect of reduced latent heat due to the addition of microparticles is also manifested during melting. According to Fig. 10b, the ratio of total energy stored by microparticle-added PCM and that by pure PCM decreases with increase in particle fraction. As far as exergy ratio is concerned, the behavior of microparticles PCMs during melting is distinct from what is observed during solidifcation. Although the same trend is seen with nanoparticles, the decrease in energy/exergy ratio is relatively more in case of microparticle PCMs. As seen earlier, the latent heat of microparticles PCM of any particle fraction is less as compared to that of its nano-counterpart. Hence, it can be stated that the reduced latent heat exerts similar effect on both the energy and exergy storage capacities. Furthermore, this is true whether it is nano or microparticles.

Conclusions

The present work investigates the influence of microsize conductivity particle dispersion on the heat transfer and exergy performances of PCM. The thermo-physical properties of composites are measured experimentally following Temperature-History technique. The phase change processes are mathematically modeled with an enthalpy-based method and the resulting system of conjugate governing equations is solved employing commercial CFD code, FLUENT. A constitutive equation for particle flux is included in the mathematical model to simulate particle migration in the PCM. The conclusions of the evaluation derived from investigations are:

  • Due to the augmentation of thermal conductivity, the discharging rate of composite PCMs is significantly high and micro particles are superior to nanoparticles in enhancing solidification rate.

  • The short coming of particles in the PCMs is exposed in the light of reduced latent heat and specific heat capacities of composites PCMs. Moreover, reduction in heat capacities is relatively high when microparticles are added.

  • From exergy performance perspective, the microparticles are superior to nanoparticles. However, opposite trend is disclosed by microparticles during melting.

  • Particles addition, however, dampens the natural convection during charging and the effect is more prominent when microparticles are dispersed as the viscosity of microparticles composite is higher than that of nanoparticles composite. However, in solar thermal applications, heat transfer enhancement is required mainly for discharging process rather than for charging. This is because heat is available at constant rate for longer period and the same has to be removed at faster rate. Hence, the microparticles addition can be stated as a promising enhancement technique for LHTS system of solar water heaters as producing hot water at faster rate in the evening and night is most critical. Moreover, using microparticles instead of nanoparticles would reduce the cost to larger extent.

  • Due to relatively larger size as compared to nanosize particles, one may expect settlement of microsize particles. Since it is demonstrated that there is always migration of microparticles, the same may overcome the settlement problem. However, this was not verified in this work which requires testing of the system for number of thermal cycles. The thermal cycle testing would be carried out in future work.

  • Hence, if non-settlement of particles is confirmed, then particle dispersion would be a better technique than other enhancement techniques i.e. improving heat exchanger design (using fins) and inserting non-moving high conductivity structures as these techniques would significantly reduce the volume of PCM in the system.