Introduction

The stock market volatility remains the main topic of concern in the financial markets in the last few decades. The estimation of volatility of stock prices holds great deal of importance among the financial institutions, academics, and policy makers. The literature well documents the estimation of stock volatility using various statistical and mathematical models like ARCH/GARCH, stochastic volatility model, realized volatility, etc. Volatility of the underlying plays a great role in the forecasting of future realized volatility and the pricing of derivative instruments. Hence, there should be the best volatility measure that contains all the information about the market’s future volatility.

There are quite good number of studies that investigates the stock markets, corporate governance, firm performance, and related financial markets during the global financial crisis (Choudhry et al. 2007; Samarakoon 2011; Kenourgios et al. 2011; Kenourgios and Padhi 2012; Liu et al. 2012). Of course, these studies are performed in both developed markets and emerging markets. However, we do not find significant studies that are associated with Indian stock markets with special reference to stock volatility. Hence, our study aims to fulfill this gap, in other words, we study the stock market volatility for the full sample and during global financial crises. The study is motivated based on some interesting works (Äijö 2008; Peng and Ng 2012; Li 2013), they analyze the most popular benchmark volatility indices (VIX, VXN, VDAX, VFTSE, VSMI, VXJ, and VSTOXX). These studies describe the term structure of implied volatility and their linkages, and financial contagion, asymmetric market dependence, market turmoil, and behavior of VIX.

Our study is based on the emerging market’s volatility index that investigates the relationship between implied volatility and future realized return volatility. The study contributes in several aspects in terms of asset pricing and volatility prediction: (i) the volatility estimate based on the VIX can be used as one of the input for Black–Scholes model to price new options; (ii) most of the previous studies rely on the historical standard deviation (historical volatility) while our study distinguishes between historical volatility and realized volatility; (iii) sometime emerging markets suffer from the poor liquidity that turns into the problem of error-in-variable (EIV) in the computation of expected volatility; hence, the study employs 2SLS procedure to control the EIV; (iv) the core contribution of the paper is of in twofold: First, it explains the relation between implied volatility and future stock market volatility in the emerging options market. Second, it extends the literature of market efficiency; (v) the study educates the volatility traders that how implied volatility (VIX) can predict the future realized volatility (30 days horizon) and the same can be used to price the options.

There are several measure of stock volatility (like historical volatility, implied volatility, conditional volatility, stochastic volatility, etc.) that is exercised by the market participants to value their financial assets and portfolio selection. Our aim of the study is to show that how ex-ante volatility (VIX) contains the information about the ex-post volatility (realized volatility) of the stocks. Unlike the previous studies (Christensen and Prabhala 1998; Christensen and Hansen 2002; Li and Yang 2009; Shaikh and Padhi 2013), our study is based on the implied volatility index (India VIX, herein after IVIX). We test the information content and market efficiency of IVIX in the prediction of future realized volatility. The novel aspect of the study is that we use longer time series and non-overlapping monthly volatility series and also distinguish between realized and historical volatility. Our results are robust because we employ 2SLS, instrumental variable technique, and linear quantile regression in the presence of EIV problem.

Some of the earlier studies (Chiras and Manaster 1978; Christensen and Prabhala 1998; Christensen and Hansen 2002; Corrado and Miller 2005; Muzzioli 2007; Li and Yang 2009; Padhi and Shaikh 2013) conclude that implied volatility subsume all the information that contained in the historical volatility. The second strand of the literature on implied volatility index also supports the previous studies. Wong and Tu (2009) conduct a study of information content of TVIX (Taiwan volatility index) and show that TVIX contains all the important information to predict the future realized volatility. Chung et al. (2011) recently examine the information content of S&P 500 VIX options and describe that information content of implied volatility from two options markets is not same. In addition, they observe that the information extracted from S&P 500 index options and the information recovered from VIX options significantly improve all the prediction on the S&P 500 index. The studies of Frijns et al. (2010) and Dowling and Muthuswamy (2005) on the Australian stock market based on implied volatility index show that the implied volatility indices contain information about both stock market return and future volatility.

More recently Giot (2003) analyzes the information content of implied volatility indices for forecasting volatility using RiskMetrics, GJR-GARCH, OLS, and instrumental variable estimation and concluded that implied volatility index provides accurate and meaningful information as to future volatility forecasts. López and Navarro (2012) in their review paper describe that volatility indices outperform in the prediction of future volatility, and they show that volatility index can be considered as investor’s-fear-gauge of fear of their portfolio.

Yang and Liu (2012) investigates the predictive power of TVIX implied volatility index in the Taiwan stock market, they show that implied volatility index also hold the predictive power to forecast the future market volatility like the implied volatility of call and put options and they conclude that TVIX is an effective indicator of future volatility in the emerging markets. The studies (Daigler and Rossi 2006; Konstantinidia et al. 2008; Szado 2009; Chung et al. 2011; Konstantinidi and Skiadopoulos 2011; Shu and Zhang 2012) have demonstrated the informational efficiency of implied volatility index and shown that volatility products (say VIX F&Os) are helpful in the price discovery and portfolio risk management.

This study investigates the informational efficiency of IVIX implied volatility index as the forecaster of future volatility. The empirical results show that IVIX is efficient to predict the realized volatility and the Nifty Options market is also efficient which impounds the market-wide information in the option prices. The Hausman test shows that IVIX is measured with errors and controlled using instrumental variable estimation. We have been estimating the consistent estimate of future volatility through 2SLS and LQR regression estimation. The study concludes that IVIX is the unbiased estimate of future volatility and contains all the important market-wide information to explain the future volatility. The study can contribute in twofolds: first, it is useful for the volatility traders who forecast the volatility in order to find out the true value of financial assets and second, this study provides some insights if NSE introduces some more derivative product on volatility index (like VIX Futures and Options) that can help the market for better price discovery and market transparency.

The rest of the article is organized as: “Data sources and methodology” section deals with the Data and Methods used to analyze the information content of implied volatility index; “Results and discussion” section describes the estimation of empirical models; “Conclusions” section concludes our paper.

Data sources and methodology

Data sources

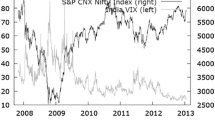
We collect the daily closing price of India VIX form the website of NSE. The sampling period starts from November 01, 2007 and ends on February 28, 2013 and the corresponding underlying stock index S&P CNX Nifty is also downloaded for the same period. The National Stock Exchange of India (NSE) has started calculating VIX index from November 2007; it is the investor’s market expectation for the near future. The India VIX uses the same methodology developed by CBOE. The implied volatility index is the ex-ante measure of volatility of the next month (about 30 calendar days) of the realized volatility.

Identification of crises period

The literature has provided various approaches to determine the crises period. The first approach is ad-hoc based on the major economic and financial events that is provided by Federal Reserve Bank Board St Louis (2009) and Bank for International Settlement (2009). Forbes and Rigoben (2002) and Baur (2012) have used an ad-hoc approach to identify the crises period for the Asian crises and GFC (Global Financial Crises). On the other hand, there is a statistical approach based on the Markov Regime Switching Model (MR-SM) to determine the crises period endogenously (e.g., Boyer et al. 2006; Baur 2012; Dimitriou et al. 2013; Dimitriou and Kenourgios 2013). According to GFC, the crises period falls in various four phases and the crises to be indentified from August 2007 to March 2009. However, when we employ the Markov regime-switching model (MR-SM) to determine the crises period endogenously for volatility series (realized volatility), the crises period falls between November 2007 to June 2009 (see Fig. 1). The MR-SM model classifies the volatility series based on the smoothed probabilities in the regimes (Regime 1 and 2), the Regime-2 in which the probabilities approaching to one shows the period of crises and the structural break after that period. Hence, the crises period is to be regarded as 2007M11–2009M06 and the stable period classified 2009M07–2013M02. The analysis of the present study is divided into sub-periods namely Period 1 regarded as full sample period that covers the monthly volatility from 2007M11 to 2013M02, Period 2 is attributed toward global financial crises took place during 2007–2009 and it starts from 2007M11 and ends on 2009M06, and the Period 3 is classified as the normal market period observed from 2009M07 to 2013M02.

Fig. 1
figure 1

Structural breaks in the volatility series. The plot of smoothed probabilities, estimated through Markov regime-switching model (MR-SM) and classified the data points in Regime-1 (Stable regime) and Regime-2 (Unstable regime)

Full size image

Variable definition

In this section, we present the variable definition and their construction.

Implied volatility (IVIX)

Implied volatility is the market’s expectation of volatility, based on the best bid and ask prices of options written on S&P CNX Nifty index. Implied volatility index is computed as the function of time-to-expiration; risk-free-rate-of-interest; forward index level, and bid-ask quotes of options. Volatility is calculated using the order book of the underlying index options and is denoted as an annualized percentage term. Stock price indices are calculated using the prices of their component stocks. While the VIX is a volatility indices comprised of the options rather than stock prices, India VIX uses the same methodology developed by the CBOE with required changes. Following equation is developed to calculate the India VIX:

$$ \sigma^{2} = \frac{2}{T}\sum\limits_{i} {\frac{{\Updelta K_{i} }}{{K_{i}^{2} }}} e^{RT} Q(K_{i} ) - \frac{1}{T}\left[ {\frac{F}{{K_{0} }} - 1} \right]^{2} $$

Description of the inputs of the formula

σ

Is the India VIX shown in the percentage term i.e., India VIX/100 \( \Rightarrow \) VIX = σ × 100

T

Time-to-expiration i.e., life of the options

F

Forward index level derived from index option prices

K 0

First strike below the forward index level, F

K i

Strike price of ith out-of-the-money option; a call if K i  > K 0 and a put if K i  < K 0; both put and call if K i  = K 0

ΔK i

Interval between strike prices – half the difference between the strike on either side of K i : \( \Updelta K_{i} = \frac{{K_{i + 1} - K_{i - 1} }}{2} \)

(Note: ΔK for the lowest strike is simply the difference between the lowest strike and the next higher strike. Likewise, ΔK for the highest strike is the difference between the highest strike and the next lower strike)

R

Risk-free-rate-of- interest to expiration (MIBOR, i.e., 30/90 days)

Q(K i )

The midpoint of the bid-ask spread for each option with strike K i

India VIX calculation measures the time-to-expiration in years, using minutes till expiration. The time-to-expiration is given by the following expression: T = {MCurrent day + MSettlement day + MOther days}/min in a year. Risk-free interest rate (R) is a Mumbai Inter Bank offered rate. The relevant tenure of NSE MIBOR rate (i.e., 30 or 90 days) is being considered as risk-free-interest rate for the respective expiry months of the Nifty option contracts. NSE has an actively traded, large and liquid Nifty futures market. Therefore, the latest available traded price of the Nifty futures of the respective expiry month is considered as the forward index level (F). For more detail, see white paper on India VIX, 2007.Footnote 1

The implied volatility is calculated in monthly non-overlapping manner as the estimate of near month future volatility (30 days expectation).

$$ \sigma_{{{\text{IVIX}} t}} \; = \;\frac{{\mathop \sum \nolimits_{i = 1}^{n} {\text{IVIX}}_{i} }}{n} $$
(1)

where i = 1, 2,…, n (closing price of IVIX for the 18–22 trading days) and t = 1, 2,…, T (months).

Realized volatility (RV)

To calculate monthly non-overlapping ex-post return volatility, we calculate continuously compounded log-return of S&P CNX Nifty equity index. The rationale behind calculating monthly volatility series is to analyze the predictive power of implied volatility indices as the forecast of future realized volatility. Realized volatility is the simple standard deviation calculated for the Nifty log-return, the period covered by the implied volatility.

$$ \sigma_{{{\text{RV}}\,t}} = \sqrt {\frac{252}{m - 1}\mathop \sum \limits_{j = 1}^{m} \left( {R_{j} - \bar{R}} \right)^{2} } $$
(2)

where \( R_{j} \; = \;{ \ln }\left( {\frac{{S_{t} }}{{S_{t-1} }}} \right) \) and \( \bar{R}\; = \;\frac{{\mathop \sum \nolimits_{j = 1}^{m} R_{j} }}{m} \) j = 1, 2,…, m (log-return of underlying Nifty index calculated for the period covered by average implied volatility).

Historical volatility (HV)

In the previous studies, historical volatility is simply taken as one period lagged value of realized volatility but for the present study, we distinguish between these two. The historical volatility is calculated for the period going back (t − 1), the same number of days that is covered by the realized volatility.

$$ \sigma_{{{\text{HV}} t}} \; = \;\sqrt {\frac{252}{m - 1}\mathop \sum \limits_{j = 1}^{m} \left( {R_{j,\;t - 1} - \bar{R}} \right)^{2} } $$
(3)

Summary statistics

Table 1 reports summary statistics on various sub-periods. The summary statistics are reported in two panels, Panel A shows for the raw values and Panel B for log-transformed values. We divide the sample period in three sub-periods namely Period 1 2007M11–2013M02, Period 2 2007M11–2009M06, and Period 3 2009M07–2013M02 (see Fig. 1 for identification of crises period). The rationale of grouping of sample is to analyze the performance of implied volatility in various trading regimes. The Period 2 is attributed as the period of global financial crises took place during 2007–2009 in the US and the Asian markets and Period 3 is the market after the crises. Table 1 shows mean, maximum, minimum, and standard deviation of various ex-ante and ex-post volatility. Starting with the mean of ex-ante volatility (IVIX), we can observe that IVIX is not identical in all sub-periods and the average IVIX during the Period 2 is found to be 40.4 % which is very high as camper to other periods. This is due to the turmoil period experienced by the Indian economy during the US sub-prime crises. At this point, we can conclude that IVIX is the investor’s-fear-gauge index and the expectation of the investors is attributed in the options trading to hedge the market holdings. The similar pattern observed for the ex-post volatility (RV and HV). Now we want to know the information content of IVIX; if the IVIX is the smoothed expectation of realized volatility, then it should conform to the realized volatility series.

Table 1 Summary statistics
Full size table

Figure 2 clearly indicates that IVIX is the best estimate of realized volatility because of IVIX moves in the same direction as realized volatility in the time series sequence, but we can see that IVIX does not conform exactly to the realized volatility in several months. This is the poor indication of information content of IVIX as the estimate of future volatility. This may be due to the potential problem of errors of measurement. Hentschel (2003) investigates the potential problem of error in implied volatility occurred due to violation of assumptions of Black–Scholes option pricing model. If the prices of the options involve measurement errors, then the estimates of implied volatility will be subject to “noise” and “biases.” Thus, error in the option prices and underlying assets price results in error in the implied volatility. To account for this error, Hentschel (2003) computes confidence intervals for implied volatility based on moneyness and expiration cycle. He shows in his study that regression of realized volatility on implied volatility gives slope of implied volatility which is different from unity and is consistent with the potential problem of measurement errors in implied volatility. Therefore, in this study, EIV problem is analyzed with the aid of instrumental variable technique and the results are discussed in the following section.

Fig. 2
figure 2

Time series plot of implied volatility, realized volatility, and historical volatility

Full size image

The maximum IVIX for the sample period is found to be 65.6 % and the minimum 13.9 %. The maximum and minimum reading of IVIX of Period 3 is more normal as on the counter part of Period 1 and 2. Generally, normal market is observed when the reading of VIX falls between 15 to 30 %. The standard deviation’s of ex-ante and ex-post volatility is not same, we see that standard deviation’s of ex-post volatility is about 52 % (Period 1) and ex-ante 35.6 %, this implies that ex-post volatilities are more volatile (Christensen and Prabhala 1998; Christensen and Hansen 2002) than the ex-post volatility. We can conclude that IVIX is the smoothed expectation of future volatility and the same results noticed for other periods.

Model specification and EIV problem

In this section, we deal with the simple OLS model specification with encompassing regression. In addition, the problem of EIV is discussed and resolved using instrumental variable estimation.

Simple OLS and encompassing regression

To analyze the information content of IVIX as the forecaster of realized volatility, following model specification are structured.

$$ \ln \sigma_{{{\text{RV}}t}} \; = \;\alpha_{ 0} \; + \;\beta_{\text{IVIX}} \;\ln \sigma_{{{\text{IVIX }}t}} + u_{t} $$
(4)
$$ \ln \sigma_{{{\text{RV}}t}} \; = \;\alpha_{ 0} \; + \;\beta_{\text{HV}} \ln \sigma_{{{\text{HV}} t}} \; + \;u_{t} $$
(5)
$$ \ln \sigma_{{{\text{RV}}t}} \; = \;\alpha_{ 0} \; + \;\beta_{{{\text{RV}} - 1}} \,\ln \sigma_{{{\text{RV}}\;t - 1}} + u_{t} $$
(6)
$$ \ln \sigma_{{{\text{RV}}t}} = \, \alpha_{ 0} + \beta_{\text{IVIX}} \,\ln \sigma_{{{\text{IVIX}} t}} + \beta_{\text{HV}} \ln \sigma_{{{\text{HV}} t}} + u_{t} $$
(7)

The testable hypothesis for the above OLS modes are (Christensen and Prabhala 1998) (i) the intercept should be zero α 0 = 0 (ii) the slope of implied volatility should not be different from one i.e., β IVIX = 1 (iii) the slope of the historical volatility and one period lagged realized volatility should not be different from zero i.e., β HV = 0 and β RV−1 = 0 (iv) in all the equations the residual term is white noise. If these underlying hypotheses are not rejected, we can conclude that implied volatility is the unbiased estimate of future volatility.

Error-in-variable problem

One of the classical assumptions of OLS regression is that the residuals are contemporaneously uncorrelated with the independent variables. In practice, hardly this assumption remains true. In the empirical study, the assumption of exogeneity of independent variable is unrealistic. When independent variables correlate with the equation’s residual term, the estimates from OLS are biased and inconsistent. The problem of EIV occurs due to violation of the assumption of no errors of measurement. More specifically, measurement error causes: first, slope of the explanatory variable remains downward biased; the intercept also overestimated (i.e., upward biased) second, when size of sample increased even though the parameters remains asymptotically biased and inconsistent. In our case, we deal with the monthly non-overlapping realized volatility and implied volatility which are subject to measurement errors. Suppose σ RVt is a linear function of implied volatility σ IVIXt .

$$ \sigma_{{{\text{RV}}t}} \; = \;\alpha_{ 0} + \alpha_{ 1} \;\sigma_{{{\text{IVIX }}t}} \; + \;\upsilon_{t} $$
(8)

where ν t  ~ N (0, \( \sigma_{\upsilon }^{2} \))

$$ {E}(\sigma_{{{\text{RV}}t}} |\sigma_{{{\text{IVIX}} t}} )\; = \;\alpha_{ 0} \; + \;\alpha_{ 1} \,\sigma_{{{\text{IVIX}}\,t}} $$

The implied volatility is subject to measurement errors due to Non-synchronous trading of underlying, jumps, bid-ask spread, infrequent trading, and so on, hence \( \sigma_{{{\text{IVIX}} t}} \) cannot be measured absolutely accurately and now denote the measured value for \( \sigma_{{{\text{IVIX}} t}} \) by \( \sigma^{\prime}_{{{\text{IVIX}} t}} \). For each observation \( \sigma^{\prime}_{{{\text{IVIX}} t}} \) equals by construction the true value \( \sigma_{{{\text{IVIX}} t}} \) plus the measurement error ut, that is (Verbeek 2004)

$$ \sigma^{\prime}_{{{\text{IVIX}} t}} = \sigma_{{{\text{IVIX }}t}} + u_{t} $$
(9)

where u t  ~ iid (0, \( \sigma_{u}^{2} \)), and u t is also independent of υ t in the model

$$ \sigma_{{{\text{RV}}t}} = \, \alpha_{ 0} + \, \alpha^{\prime}_{ 1} \;\sigma^{\prime}_{{{\text{IVIX}} t}} + e_{\text{t}} $$
(10)

where e t  = υ t  −  α1 u t .

Now, α1 estimated as,

$$ \hat{\alpha }_{1} \; = \;\frac{{\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}}t}} \; - \;\bar{\sigma }_{\text{IVIX}} } \right)\left( {\sigma_{{{\text{RV}}t}} - \bar{\sigma }_{\text{RV}} } \right)}}{{\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} \; - \;\bar{\sigma }_{\text{IVIX}} } \right)^{2} }} $$
(11)

Substituting Eq. 10, we have,

$$ \hat{\alpha }_{1} = \alpha_{ 1} + \frac{{\left( \frac{1}{T} \right)\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} \; - \;\bar{\sigma }_{\text{IVIX}} } \right)\left( {e_{t} - \bar{e}} \right)}}{{\left( \frac{1}{T} \right)\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} - \bar{\sigma }_{\text{IVIX}} } \right)^{2} }} $$
(12)

as T → ∞, sample statistic approaches to population parameter. Thus,

$$ \begin{aligned} {\text{plim}}\,\hat{\alpha }_{ 1} & \; = \;\alpha_{ 1} + \frac{{{\text{plim}}\left( \frac{1}{T} \right)\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}}t}} \; - \; \bar{\sigma }_{\text{IVIX}} } \right)\left( {e_{t} \; - \;\bar{e}} \right)}}{{{\text{plim}}\left( \frac{1}{T} \right)\mathop \sum \nolimits_{t = 1}^{T} \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} - \bar{\sigma }_{\text{IVIX}} } \right)^{2} }} \\ \; & = \;\alpha_{ 1} \; + \;\frac{{E \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} .e_{t} } \right)}}{{V \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} } \right)}}\; \ne \;0 \\ \end{aligned} $$
(13)

where

$$ \begin{aligned} {E} \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} \cdot e_{t} } \right) & \; = \;{E}\left( {\sigma_{{{\text{IVIX }}t}} + u_{t} } \right),\;\left( {\upsilon_{t} - \alpha_{1} u_{t} } \right) \\ & { = } - \alpha_{1} \sigma_{u}^{2} \;{\text{and}} \\ \end{aligned} $$
$$ \begin{aligned} V \left( {\sigma^{\prime}_{{{\text{IVIX}} t}} } \right) & \; = \;{\text{V}}\left( {\sigma_{{{\text{IVIX}} t}} + u_{t} } \right), \\ & = \sigma_{IVIX}^{2} + \sigma_{u}^{2} \\ \end{aligned} $$

Hence,Footnote 2

$$ {\text{plim}}\,\hat{\alpha }_{1} = \alpha_{ 1} \left( {1 - \frac{{\sigma_{u}^{2} }}{{\sigma_{\text{IVIX}}^{2} + \sigma_{u}^{2} }}} \right) $$
(14)
$$ \begin{aligned} {\text{plim}}\left( {\hat{\alpha }_{1} - \alpha_{1} } \right) & = {\text{plim}}\left( {\bar{\sigma }_{{{\text{RV}}t}} - \alpha_{1} \;\sigma^{\prime}_{{{\text{IVIX}} t}} - {E}\left\{ {\sigma_{{{\text{RV }}t}} } \right\} + \alpha_{1} {E}\left\{ {\sigma_{{{\text{IVIX }}t}} } \right\}} \right) \\ & = - {\text{ plim}}\left( {\hat{\alpha }_{1} - \alpha_{1} } \right){E}\,\left\{ {\sigma^{\prime}_{{{\text{IVIX}} t}} } \right\} \\ \end{aligned} $$
(15)

The problem of inconsistency arises when E \( \left\{ {\sigma^{\prime}_{{{\text{IVIX}} t}} } \right\} \) > 0, that is overestimation of the slope and underestimation of intercept term.

Single equation estimation (SEE)

At this stage, we come to know that in the presence of EIV, we cannot obtain consistent estimate; hence, we use some robust mathematical techniques that take into accounts the presence of measurement error and give consistent estimate. Theil (1953) and Basmann (1957) developed some estimation method known as single equation method, is applied to one equation of the system at a time. Here, we discuss the Two-Stage Least Squares (2SLS) and instrumental variable method to resolve such measurement problem. The 2SLS method is similar to the instrumental variable method in which we obtain fitted values of endogenous variable \( \left\{ {\hat{\sigma }_{{{\text{IVIX}}t}} } \right\} \) as instruments for the corresponding observed values \( \left\{ {\sigma_{{{\text{IVIX}}t}} } \right\} \) along with the exogenous variable (say \( \left\{ {\sigma_{{{\text{HV}}t}} } \right\} \) included in the function serving as their own instruments (Koutsoyiannis 1973).

2SLS and instrumental variable estimation

Here, we illustrate the 2SLS procedure in terms of our economic variable of interest implied volatility index \( \left\{ {\sigma_{{{\text{IVIX }}t}} } \right\} \) and realized volatility \( \left\{ {\sigma_{{{\text{RV }}t}} } \right\} \).

Step 1 diagnose EIV

We employ Hausman (1978) specification test to diagnose the presence of EIV. Hausman suggested the following auxiliary regression to diagnose the EIV. In practice, finding exact instrument for the endogenous variable is difficult; hence, we take one period lagged values of \( \{ \sigma_{{{\text{IVIX }}t}} \} \) and \( \left\{ {\sigma_{RVt} } \right\} \) as instrument for the suspected variable \( \{ \sigma_{{{\text{IVIX}}t}} \} \).

Stage 1 regression model

$$ \sigma_{{{\text{IVIX 1}}t}} = \delta_{ 0} + \delta_{ 1} \,\sigma_{{{\text{IVIX }}t - 1}} + \delta_{ 2} \,\sigma_{{{\text{HV }}t}} + \in_{t} $$

Stage 2 stores the values of \( \in_{t} \) and runs the following regression

$$ \sigma_{{{\text{RV}}t}} = \beta_{ 0} + \beta_{ 1} \sigma_{{{\text{IVIX}}t}} + \beta_{ 2} \sigma_{{{\text{HV }}t}} + \beta_{ 3} \in_{t} \; + \;\omega_{t} $$
(16)

Stage 3 tests the null β 3 = 0 versus β 3 ≠ 0, rejecting a null β 3 = 0, signifies that \( \sigma_{{{\text{IVIX}}t}} \) is measured with errors.

Step 2 2SLS estimation

Stage 1 First stage OLS estimation

In first stage OLS, we obtain the fitted values of \( \sigma_{{{\text{IVIX}}t}} \). We follow the procedure adopted by Christensen and Prabhala (1998), Hansen (2001), and Christensen and Hansen (2002). We choose one/two period lagged values of \( \sigma_{{{\text{IVIX}}t}} \) and exogenous variable \( \sigma_{{{\text{HV}}t}} \) as an instrument.Footnote 3

$$ \hat{\sigma }_{{{\text{IVIX}}t}} \; = \;\beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t - 1}} + \beta_{2} \sigma_{{{\text{IVIX}}t - 2}} + \beta_{3} \sigma_{{{\text{HV}}t}} + u_{t} $$
(17)

Stage 2 Second stage of OLS estimation

$$ \sigma_{{{\text{RV}}t}} = \beta_{0} + \beta_{\text{IVIX}} \hat{\sigma}_{{{\text{IVIX}}t}} + \in_{t} $$
(18)
$$ \sigma_{{{\text{RV}}t}} = \beta_{0} + \beta_{\text{IVIX}} \,\hat{\sigma }_{{{\text{IVIX}}t}} + \beta_{\text{HV}} \sigma_{{{\text{HV}}t}} + \in_{t} $$
(19)
Step 3 Hypothesis tests

To compare consistency of estimate from OLS to 2SLS, we calculate Hausman H-statistic with one degrees of freedom H-stat = \( \frac{{\left| {\beta^{{2{\text{SLS}}}} - \beta^{\text{OLS}} } \right|}}{{V\left( {\beta^{{ 2 {\text{SLS}}}} } \right) - V (\beta^{\text{OLS}} )}} \): Ho: OLS estimate are consistent versus 2SLS estimate are consistent. Rejecting the null implies that there is potential noise in the implied volatility and 2SLS estimate are more consistent than simple OLS.

Linear quantile regression

LQR is a generalization of median regression, the regression that predicts the conditional τ-quantile of the dependent variable. If LQR shows that the conditional quintiles behave in manner quite different from the conditional mean, this suggests that OLS estimation is problematic. OLS estimation only provides a prediction of the conditional mean, but finding several quantile regression lines gives more comprehensive idea of the joint distribution of the data. Alexander (2008) pointed out that LQR is a natural extension of OLS where the optimization objective of minimizing the residual sum of squares is replaced by an asymmetric objective. We illustrate the LQR regression model in terms of dependent variable \( \sigma_{{{\text{RV}}t}} \) and independent variable \( \sigma_{{{\text{IVIX}}t}} \). The simple OLS model is

$$ \sigma_{{{\text{RV}}t}} = \beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}} + \in_{t} $$
(20)

Here, the parameter β 0 and β 1 are the constant and \( \in_{t} \) ~ iid and \( \in_{t} \) is independent of \( \sigma_{{{\text{IVIX}}t}} \). The parameters are estimated subject of the optimization problem:

$$ \mathop {\hbox{min} }\limits_{{\beta_{0} , \beta_{1} }} \mathop \sum \limits_{t = 1}^{T} \left( {\sigma_{{{\text{RV}}t}} - \{ \beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}} \} } \right)^{2} $$
(21)

The most convenient way to describe the conditional distribution of the dependent variable is using its quantile. In quantile estimation, we still assume \( \in_{t} \) ~ iid. But, we must introduce a specific error distribution function denoted \( F_{ \in } \). Let τ lies between 0 to 1 and denoted the τ-quintiles of the error \( F_{ \in }^{ - 1} \) (τ). Also, the conditional τ-quintiles of the dependent variable \( \sigma_{{{\text{RV}}t}} \), which is found from the inverse of F (\( \sigma_{{{\text{RV}}t}} \) | \( \sigma_{{{\text{IVIX}}t}} \)), by F −1 (τ | \( \sigma_{{{\text{IVIX}}t}} \)). Now taking conditional τ-quintiles of Eq. 20

$$ F^{ - 1} (\tau |\sigma_{{{\text{IVIX}}t}} \,) = \beta_{o} + \beta_{1} \sigma_{{{\text{IVIX}}t}} + F_{ \in }^{ - 1} \,\left( \tau \right) $$
(22)

This is the simple LQR model, as we minimize the residual sum of squares (SSR) in Eq. 21. In quantile regression, we also find the τ-quintiles regression coefficient as a solution to an optimum problem.

$$ \mathop {\hbox{min} }\limits_{{\beta_{o} , \beta_{1}}} \,\mathop \sum \limits_{t = 1}^{T} \left( {\tau - 1_{{\sigma_{{{\text{RV}}t}} \le \beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}} }} } \right)\left( {\sigma_{{{\text{RV}}t}} - \left( {\beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}}} \right)} \right) $$
(23)

where

$$ \,1_{{\sigma_{{{\text{RV}}t}} \le \beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}} }} = \left\{ {{}_{0}^{1} {}_{\quad \text{otherwise }}^{{\quad if \sigma_{{{\text{RV}}t}} \le \beta_{0} + \beta_{1} \sigma_{{{\text{IVIX}}t}}}}} \right. $$

The constant β 0 and β 1 estimated using the methodology introduced by Koenker and Bassett (1978)

Empirical results and discussion

Table 2 reports the simple OLS and encompassing regression results. As per the classification discussed in the summary statistics, the regression outputs are divided in three panels. Now starting with the Panel A, the first line clearly shows that implied volatility index (IVIX) subsumes the information about future volatility with the slope of 1.32 and intercept 0.20. This implies that implied volatility is the best estimate of realized volatility and Indian options market is an efficient market that contains the investors’ sentiment and market-wide information in the options prices. But, as per our null hypothesis the slope of IVIX is different from one and intercept is not zero. The slope of implied volatility index is more than one; this indicates that IVIX over-estimates the realized volatility. At this point, we can conclude that implied volatility is the biased estimate of future volatility.

Table 2 Simple OLS and encompassing regression
Full size table

In the superiority of historical volatility and implied volatility, we run one more regression as shown in the second line of Panel A, we can notice the slope of historical volatility is 0.76 and statistically significant. This indicates that historical volatility also contains some information to explain the future volatility. But, we can see that the slope of historical volatility is less than the slope of implied volatility; hence, we can say that implied volatility is more superior than the historical volatility. The similar result is obtained for the encompassing (Christensen and Prabhala 1998) regression. Now we run the regression with implied and historical volatility as regressors. The fourth line of the Panel A shows the estimate of implied volatility and historical volatility, respectively, 1.50 and −0.14. In this multiple regression, the slope of realized volatility does not appear statistically significant and implied volatility dominates the historical volatility. Consequently, we can conclude that implied volatility is the smoothed expectation of future volatility. The historical volatility does not contain important information what already contained in the options prices.

Panel B of Table 2 reports the regression output during the market turmoil took place during the period 2007–2009. The slope of implied volatility is found to be 1.19 and statistically significant, but less than the slope of other periods. This indicates that IVIX is more biased during the financial crisis and the regime takes place in the market shift (Christensen and Prabhala 1998). In addition, we can also observe that the historical volatility and lagged realized volatility does not appear statistically significant. This phenomenon explains that historical volatility does not possess good explanatory power to predict the future volatility during the market crises period.

Now moving on the Panel C of Table 2, that explains the predictive power of implied volatility index during the normal market. The first row of the Panel C reports the slope of implied volatility 1.21 which is highly statistically significant, while second and third row shows the slope of historical and lagged realized volatility (0.62). It is seen clearly that during the normal market period implied volatility dominates the ex-post volatility as the best estimate of future volatility. This also clears that IVIX is the best measure of market expectation which gauge the expectation of investors. Finally, the last row shows that historical volatility appeared almost zero and the slope of implied volatility is 1.22. The important observation in all the regression is that the adj. R 2 is high (73 %) for IVIX regression model. The LM-stat (for all panels of Table 2) shows that OLS results are not suffering from the problem of autocorrelation.

Table 3 shows the estimation results of EIV problem. We use the specification suggested by Hausman (1978) to diagnose the problem of EIV. In the first stage OLS, we use the instruments: intercept, lagged implied volatility, and historical volatility and implied volatility as dependent variable. We store the value of residuals \( \in_{t} \) and include it as regressor in the auxiliary regression. The Panel B clearly shows the slope of \( \in_{t} \) is 0.90 and statistically significant. The regression result strongly suggests that there is measurement error in the calculation of IVIX. Hence, the estimation is performed in the single equation 2SLS mechanism.

Table 3 EIV regression
Full size table

Table 4 reports the 2SLS estimation for the full sample period. The Panel A shows that the first stage OLS estimation in which the fitted values of implied volatility is obtained. We run variants of regression by taking appropriate instruments in order to maximize the adj. R 2. We chose that fitted values that having highest adj. R 2 (i.e., 0.83). The 2SLS output is reported in the Panel B of Table 4. In the first row, we can see that the slope of implied volatility is estimated 1.22 with intercept 0.07. The slope is statistically significant but intercept is not significant. In addition, we calculate the H-stat (10.10) which is also highly statistically significant. At this stage, we can say that IVIX is the measured with the errors and the true estimated slope of IVIX is 1.22. To test the null that the slope of IVIX is one, we calculate Wald F-stat (i.e., F-stat(1,60) = 7.23) and is insignificant at 10 % level of significance. In addition, in the superiority of historical volatility and implied volatility, we run one more regression as shown in the second line of Panel B with historical volatility. We found that the historical volatility do not appear statistically significant. The slope of IVIX is 0.82 (Wald F-stat(1,59) = 0.297, insignificant) and intercept is about zero. Finally, we can conclude that India VIX is the best estimate of future realized volatility. The historical volatility do not impounds the important information what already contained in the implied volatility. It is also concluded that the implied volatility is measured with errors and it is controlled through instrumental variable estimation. The Wald test signifies that implied volatility is the unbiased estimate of future realized return volatility.

Table 4 2SLS regression
Full size table

Table 5 reports the LQR estimation output on the information content of IVIX as the estimate of future volatility. The LQR provides more robust estimate as compare to OLS estimation. Starting with the intercept (for τ-quintiles = 0.4, 0.6, 0.7, 0.8 and 0.9), it remains statistically significant, but for the rest of Tau it is not significant. Now analyzing the slope of IVIX for various Tau, we can observe that for all Tau’s slopes appeared statistically significant and for Tau = 0.1 and 0.2, the slope is estimated about 1.22 which is in support of our 2SLS estimation. This indicates that LQR also provides the consistent estimate in the presence of EIV. The slope of historical volatility do not appear statistically significant; hence, LQR estimation also clears that implied volatility is the best forecaster of future volatility and impounds all the important market wide information.

Table 5 Linear quantile regression
Full size table

Conclusions

This study introduces the implied volatility index (IVIX) as the forecaster of future volatility. This paper takes different approach to investigate the information content of IVIX using the EIV, instrumental variable technique, 2SLS, and quantile regression in order to obtain the robust estimate of future realized return volatility. The principal objective of this study is to show that India VIX is the investor’s-fear-gauge index and is the best forecast of market volatility in near term.

The empirical analysis provided some insights that India VIX is the unbiased estimate of future realized volatility. The investor’s future expectation about volatility is gauged in the IVIX. Our results are robust and obtained through 2SLS and quantile regression. The Hausman test showed that implied volatility is measured with errors. The estimate of IVIX obtained through 2SLS/LQR is more consistent than the traditional OLS results. The implied volatility index can be considered as one of the leading measure of market participants about the future uncertainty. The empirical results are in favor of implied volatility as the best forecaster of realized volatility. The implied volatility dominates the historical volatility and contains good amount of information to predict the future market volatility.

The practical implication of our study to the local/international investors and policy maker are: (i) the study holds an important implication for the portfolio analysts, those are investing from Asia and pacific region in the emerging markets like India; (ii) implied volatility index (e.g., India VIX) is the investor fear gauge index for the Indian capital market that provide future volatility insights to the volatility traders and policy makers;(iii) the study can effectively demonstrated in the risk management practices like value-at-risk measurement; (iv) particularly, the information content of implied volatility indices is an important study that has the implication on derivatives pricing (.i.e., Futures and Options) written on the stock index as well and on the volatility index. The study can contribute in better understating of relationship between ex-ante and ex-post volatility. In addition, NSE can promote some more volatility products like Futures and Options on India VIX to gauge the sentiments of investor about the future volatility. Finally, the study can be benefitted to the traders who trade in the volatility products and portfolio risk management.