1 Introduction

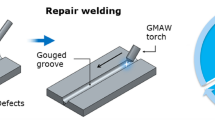
The use of modern high-strength fine-grained structural steels is necessary for the sustainable and resource-efficient production of wind turbines. This applies to both the wind turbines themselves and the mobile or ship cranes required for their erection [2,3,4,5], see Fig. 1a. Without their high load-bearing capacities combined with the enormous boom lengths required at the same time, the economic implementation of the goals for energy transformation and climate action targets is inconceivable. The use of high-strength steels poses high challenges for welding production, which are currently being investigated within the scope of numerous research projects [6,7,8]. Depending on the application, manufacturers and operators of high-strength steel structures have to meet high requirements in terms of weld joint safety and quality in accordance with the relevant standards. This involves a continuous non-destructive testing of the welds during the manufacturing process for approval and in the further life cycle. If critical defects and imperfections are found, there is the option of local gouging of the defective areas with subsequent repair welding of the groove [9]. Thermal gouging e.g. with an electric carbon arc, is most commonly used with regard to good defect detection and short gouging times [10]. In this process, the weld metal is melted with a graphite electrode and the slag is blown out with compressed air, see Fig. 1b. The resulting U-shaped groove is typically prepared for rewelding by means of peening. Subsequently, the groove can be repair welded.

Fig. 1
figure 1

a Erection of wind energy plants using mobile cranes, b scheme of a typical repair process

Full size image

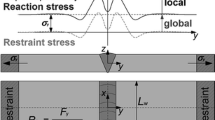
In practice, decisions on the feasibility of a safe repair weld, as well as on the procedure, are mostly based on empirical values and the know-how of the manufacturing companies. Standards and regulations on weld qualification hardly give any concrete indications on an adequate repair strategy, and there is currently no consistent scientific data base to support this. As a result of repeated thermal loading, over-proportional degradation of the microstructure is to be expected [11]. During repair welding of the joint grooves, high local shrinkage restraint and global rigidity conditions are oftentimes the case due to the surrounding structure, leading to elevated residual stresses [12, 13]. These stresses during repair welding are particularly critical in high-strength fine-grained structural steels with regard to renewed cracking due to the specific properties and microstructure as well as the low strain reserves [10]. In addition to the local, primarily material- and process-related welding residual stresses, reaction stresses occur as a result of restraint conditions in repair welding, and lead to a complex superposition of the stresses in the weld area [14]. Therefore, a quantification of the design-induced restraint conditions of welds is necessary. For this purpose, the restraint intensity concept was established by Satoh [15, 16] and further developed [17]. The restraint intensity is based on an analytical shrinkage force model transverse to the weld, where the weld length is much larger than the plate thickness. The resulting transverse force Fy is related to the weld length LS. In the model, the material behaviour is approximated to such an extent that the base material behaves linearly elastically and the weld metal bilinearly elastic-plastically. The total transverse shrinkage 2Δy results as the sum of the shrinkage of the base material 2ΔyGW and the filler metal 2ΔySG. By definition, the restraint intensity in the transverse direction of the weld RFy,i is the component stiffness towards the weld seam based on the weld length i.e. the ratio of the force per weld length Fy,i /LS to the transverse shrinkage 2Δy, see Eq. 1:

$${R}_{\textrm{Fy}}=\left(E\cdot H\right)/{L}_{\textrm{S}}={F}_{\textrm{y}}/\left(\left(\Delta {y}_1+\Delta {y}_2\right)\cdot {L}_{\textrm{S}}\right)\textrm{in}\ \textrm{kN}\cdot{\left(\textrm{mm}\cdot\textrm{mm}\right)}^{-1}$$
(1)

with Young’s modulus E, plate thickness or seam height H, displacement of both weld seam flank Δy1 and Δy2. Restraint conditions from real welding details or assembly groups can thus be transferred to component-like welding experiments by means of special testing methods. Based on several numerical studies and welding tests under defined shrinkage restraint in special testing facilities [14, 18,19,20,21], it was shown that the restraint intensity has a significant influence on the weld-induced stresses. In previous studies on repair welding, thewelding residual stresses were analysed on laboratory specimens [10]. However, due to the minor dimensions and design of the laboratory specimens, these could not be systematically related to the restraint and bending restraint intensities. In addition, numerical studies based on restraint intensity calculations for established cold-cracking tests depending on their dimensions showed that an analysis of the interaction between heat control, design and material aspects is only achievable by adapting the component-related test conditions, which represent the supporting effects and heat dissipation conditions of real components [21]. Thus, a significant deficit using small-scale experiments are divergent temperature distributions, which does not form a near- and far-field on a small scale.

Therefore, this first part of the investigations addresses the analysis and transferability of the restraint conditions in repair welding. The performed test welds serve as reference specimens in order to analyse and evaluate the residual stresses isolated with the corresponding defined shrinkage restraint and were thus prepared by milling the weld test seam or the slots to be welded in the test plates. Effort of the investigations in this work are the effects on the welding-induced residual stresses and cold cracking risk when additional hydrogen sources are considered at the welding process. The microstructure due to gouging and repair welding as well as residual stress optimisation by means of adapted heat control concepts will be focused in the second part of our investigation [1].

2 Component analysis

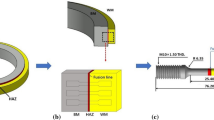
Based on recent studies [19] in this work numerical and experimental analyses of the structural stiffness were performed on near-component test specimens, and on real welded assemblies to assure the transferability of the weld test results to actual repair cases in the industry. This was done using the concept of restraint intensity to quantify the design related shrinkage restraint [16]. For this purpose, a welding assembly detail of a mobile crane was selected as a typical repair case, Fig. 2. The construction of the superstructure was abstracted into a simplified FE shell model. Then the weld was loaded in the model with a distributed load of p=100 N/mm2 transverse to the welding direction. The FE analysis and dimensions allowed the determination of the average deformations Δy1 and Δy2 (displacement of the both weld seam flanks orthogonal to the weld direction) of the weld surfaces due to the load and the stiffness of the surrounding structure. With the average deformation and the total load Fy, the restraint intensity, based on the (repair) weld length (LA=)LS=125 mm, is calculated approx. RFy=25 kN/(mm mm); see Eq. 1.

Fig. 2
figure 2

Restraint analysis of an actual weld assembly of high-strength steel S960QL, mobile crane with an assumed gouging groove to be repaired (turning gear connection)

Full size image

On the basis of this analysis and results, a parameter study according to the results in [21] could be carried out analogously using self-strained test specimens. The geometric dimensions such as length, width, plate thickness, seam form, seam configuration and seam length were varied for slot specimens. Based on the results of solid FE models, these were transferred to models using shell elements in order to allow a straightforward transferability analysis. As in previous investigations [14], it has been shown that the restraint intensity in the repair weld details considered is relatively independent of the seam shape, and thus, I-seams based on shell FE models are suitable for obtaining sufficient estimates of the rigidity conditions.

A parameter study with shell models led to the specimen design and analysis results shown in Fig. 3, which overall resulted in specimen shapes in the form of slot specimens that are suitable for large-scale welding tests and subsequent residual stress analyses due to good handling and at the same time provide component-relevant shrinkage restraints. In addition, the slot length can be adjusted to a defined restraint intensity to obtain equidistant factor intervals within the scope of the design of experiments. Thus, for the further welding experiments, to analyse the effect of restraint intensity on welding stresses and cold cracking risk, the specimen types according to Fig. 3 were specified to P1 (free shrinking test specimen) RFy=0 kN/(mm mm), P2 (slot specimen with LS=200 mm) RFy=10 kN/(mm mm) and P3 (slot specimen with LS=125 mm) RFy=20 kN/(mm mm).

Fig. 3
figure 3

a Specimen shapes selected via numerical restraint analysis for weld tests, free shrinking (P1) and self restrained (P2, P3), b exemplary half model of slot specimens for structural mechanics simulation, c restraint intensity vs. slot length, numerically determined, and selected slot lengths for the weld tests

Full size image

The experimental verification of the numerical restraint analyses was carried out by means of special slot specimens of the same dimensions made with I-weld seams, Fig. 4. Defined forces could be applied to the seam flanks by means of a hydraulic spreader. The deformations in the weld area were determined by means of digital image correlation techniques. Analogous to the numerical calculations using Eq. 1, the restraint intensity was determined. The results of the experimentally determined degrees of restraint are for P2 (slot specimen with LS=200 mm, RFy=9.9 kN/(mm mm)) and P3 (slot specimen with LS=125 mm, RFy=20.4 kN/(mm mm)). The deviations of <10% show a very good agreement of the experiments with the numerical calculations.

Fig. 4
figure 4

Experimental restraint analysis on slot specimens using digital image correlation technique, a experimental set-up, b result of the areal displacement measurement around the slot

Full size image

3 Welding experiments

In the experiments, free shrinking and self-restrained slot specimens made of base materials (BM) S500MLO (EN 10225-1) and S960QL (EN 10025-6) were welded with solid wires G 50 7 M21 4Mo (ISO 12341) and G 89 6 M Mn4Ni2CrMo (ISO 16834-A), respectively, using machanised MAG welding, cf. Fig. 5. Table 1 presents the chemical compositions and mechanical properties of the applied steel grades and weld metal (WM).

Fig. 5
figure 5

a Test set-up of the welding experiments, b welding and heat control parameters for the test welds including weld seam build-up and weld beads with additional hydrogen introduction (with preheat temperature Tp, interpass temperature Ti, welding voltage and current U or I, welding speed vs, wire feed speed vD and heat input E)

Full size image
Table 1 Chemical composition of BM, deposited WM (measured via optical emission spectrometer, Fe balanced) and mechanical properties (0.2% yield strength, Rp0.2, ultimate tensile strength Rm, elongation at fracture A5 at room temperature; Charpy-notched impact strength Av at given temperature)
Full size table

The test parameters were selected according to [2] based on the cooling times recommended by the manufacturer and preliminary tests on free shrinking specimens, cf. Fig. 5. The specimens were preheated in advance using an autogenous burner. The temperature measurement (monitoring of the interpass temperature) during welding was carried out using thermocouples. With a two-colour pyrometer (measuring range: 150–1500 °C), the temperature could be registered directly on the weld bead to determine the cooling time. The welding was carried out with uniform parameters for the free shrinking specimen and for the self-restrained slot specimens with the weld lengths LS = 200 mm and 125 mm, see Fig. 3. All weld tests were performed with and without an additional introduction of hydrogen. The hydrogen introduction during welding was realised by using water based anti-spatter spray, which was sprayed into the MAG torch after root welding and further after every weld bead, cf. Fig. 5, to illustrate a typical case or source of error during welding in the application.

The resulting residual stresses were analysed using X-ray diffraction (XRD) [22], cf. Fig. 6, at all specimens welded without additional hydrogen source. Two XRD systems were used for this purpose: (1) On a selected slot specimen (P3: LS=125 mm), the transverse, longitudinal and shear stresses were measured 2-dimensionally over the specimen surface using a robotic XRD system. The residual stresses were determined applying a linear least square analysis of the sin2Ψ-law (Dölle-Hauk equation) by using 19Ψ (-45° to 45°) and 3φ (0°, 60°, 120°) tilts each. (2) For the major number of the different specimens, the transverse residual stresses were analysed along a measuring track at the specimen centre axis transverse to the welding direction (up to ±100 mm from the weld centre). Here, a semi-automatic XRD system was used, applying the sin2Ψ-method (CrKα; collimator: D=2 mm; Ψ-steps: 7; Ψ-range: ±45°).

Fig. 6
figure 6

XRD set-up for residual stress analysis: a semi-automatic measuring system, b robotic system

Full size image

4 Results

4.1 Welding results

Figure 7a shows weld cross-sections for S500MLO/G50 and S906QL/G89 of the specimens with the highest restraint (P3, cf. Figs. 3 and 7d). For all tests, defect-free welds were achieved without additional hydrogen source. Corresponding to this, in Fig. 7b, maps of the low force Vickers hardness measurements (HV0.5) are presented, determined using ultrasonic contact impedance method (UCI). The higher strength steel S960QL/G89 was welded with cooling times of approx. Δt8/5=7 s, cf. Figs. 7c and 5b, and shows an overall higher hardness level, with values above 400 HV0.5 in the last welded cap bead and down to approx. 200 HV0.5 in the softening zone in the HAZ of the BM compared to S500MLO. The steel grade S500MLO/G50 was welded with cooling times of approx. Δt8/5=14 s, cf. Figs. 7c and 5b, and shows hardness values in the range of approx. 220 HV0.5 to 250 HV0.5. A significant softened zone in the HAZ in the base metal with hardness values of 180–200 HV0.5 can be observed.

Fig. 7
figure 7

Welds of two different steel grades: a transverse sections, b hardness maps; c determined cooling time Δt8/5 vs. interpass temperature and heat input, d welded slot specimen (type P3)

Full size image

4.2 Residual stresses

Figure 8 shows the transverse residual stress distributions for the welds of S500MLO/G50 (without additional hydrogen source) for the free shrinking specimen (a) the self-restrained specimens (b) and the longitudinal residual stress distributions for the free shrinking weld (c).

Fig. 8
figure 8

a Residual stress profiles σrs(y) of S500MLO/G50 welds in transverse direction y for a free shrinking P1, b self-restrained specimens P2 and P3, and c for P1 in longitudinal direction

Full size image

All graphs, cf. Fig. 8, represent typical residual stress distributions for transformable steels according to the known model concepts [23, 24]. The highest tensile residual stresses in the transverse direction of the free shrinking specimen (P1, cf. Fig. 8a) of approx. 150 to 200 MPa typically occur in the WM and are located a few millimetres from the weld transition to the BM. The centre lines of the two cap beads show a stress dip, which can be traced back to the phase transformation from austenite to bainitic or martensitic structure and reach residual compressive stresses of up to −100 MPa in the weld metal. The HAZ is characterised by further residual stress minima near the weld transition, which reach residual stresses of up to 0 MPa. In the course of the HAZ with increasing distance from the seam transition, the residual stresses rise to clear secondary maxima of over 150 MPa. The residual stresses decrease to the initial state in the direction of the unaffected base material, in this case steadily to about 0 MPa.

Figure 8b shows the transverse residual stress distributions σrsy(y) across the welds at x=0 mm (weld centre) for the welding tests on the slot specimens P2 and P3 made of S500MLO. The restraint transverse to the weld results in higher residual stress profiles compared to the free shrinking specimens. In the WM maximum tensile residual stresses reaches up to almost 350 MPa for the medium restraint RFy=10 kN/(mm mm) and up to 400 MPa for the highest restraint RFy=20 kN/(mm mm). Transformation and quenching effects cause local settling below 0 MPa at the medium restraint specimen (P2). At the high restraint (P3), the dip and thus the effect due to transformation and quenching is less pronounced. The restraint causes a superposition of the reaction stresses [25, 19]. The residual stress distributions of the two welded slot specimens (P2 and P3) show increased transverse residual stresses in the area of the HAZ and the BM compared to the free shrinking weld specimen. Compared to P2, P3 causes an increase in the reaction stresses from about 100 to 150 MPa in the BM and from approx. 200 to 250 MPa in the HAZ, cf. Fig. 8b. At increasing distance from the weld (y=100 mm), the tensile residual stresses approach the initial state of 0 MPa.

The tensile residual stress maxima in the longitudinal direction, cf. Fig. 8c, of up to 400 MPa occur in the WM at a distance of a few millimetres from the centre line of the cap beads and in the areas of the weld transition to the HAZ. The areas of the centre lines as well as the transition area of the two cap beads are characterised by a dip in the longitudinal residual stress profile due to local effects, such as for these steels characteristic phase transformation [23, 24]. Furthermore, local secondary maxima are formed in the HAZ to approx. 150 MPa on the side of the last welded cap bead and almost 400 MPa on the side of the first welded cap bead. In the further course, the residual stresses drop into the negative range due to compensating compressive residual stresses or to the initial state.

Figure 9 shows the residual stress distribution maps in the longitudinal and transverse direction in the weld area of the slotted specimen P3 made of S500MLO/G50 analysed by means of automated XRD. Tensile residual stresses of up to 300 MPa can be observed in the weld metal, which decrease towards the beginning and end of the weld. In addition to the weld, the transverse residual stresses are highest near the centre of the weld (x=0 mm). At a greater distance (y=100 mm), the transverse residual stresses return to the initial state of approx. 0 MPa. A similar behaviour can be observed for the longitudinal residual stresses, with maximum amounts in the range of the material strength. Since there is no additional restraint in welding direction, the longitudinal residual stresses return to their initial state of approx. 0 MPa already at a distance of about 30 mm from the weld centre line.

Fig. 9
figure 9

Residual stress maps σrs(x,y) of a S500MLO/G50 weld vicinity for self-restrained specimen P3

Full size image

In Fig. 10, the residual stress distributions for the welds of S960QL/G89 (without additional hydrogen source) for all defect free welds of the free shrinking specimens (a), the self-restrained specimens (b) and the longitudinal residual stress distributions for the free shrinking welds (c) are shown.

Fig. 10
figure 10

a Residual stress profiles σrs(y) of S960QL/G89 welds in transverse direction y for a free shrinking P1, b self-restrained specimens P2 and P3, and c for P1 in longitudinal direction

Full size image

All graphs show residual stress distributions typical for transformable steels according to the known models [23], as it was the case for steel grade S500MLO/G50. In the transverse direction of the unrestraint specimen, cf. Fig. 10a, the highest tensile residual stresses typically occur in the weld metal at a distance of a few millimetres from the centre line of the last welded cap bead. In the weld metal, these reach approx. 250 MPa. The centre of the last cap bead shows a dip, which is characteristic for the phase transformation from austenite to bainite or martensite. In the WM, this reaches residuals stresses of up to 100 MPa. The HAZ is characterised by further residual stress minima near the weld transition, which reach compressive residual stresses of about −100 MPa. In the course of the HAZ with increasing distance from the weld transition, the residual stresses increase to approx. 50 MPa up to 100 MPa. In the direction of the unaffected base material, the residual stresses then drop to the initial state, in this case steadily over the plate surface to approx. 0 MPa.

Figure 10b shows the transverse residual stress distributions σrsy(y) across the welds at x=0 mm (weld centre) for the weld tests on the slot specimens (S960QL/G89) P2 and P3. The restraint in the transverse direction of the weld results in a higher residual stress profile with higher maximum tensile residual stresses in the weld metal of about 650 MPa. Transformation and quenching effects cause localised stress dips of down to approx. −150 MPa. Furthermore, according to the model concepts, a principal superposition of the reaction stresses can be assumed due to the support effects resulting from the restraint conditions of the specimens [11]. In the case of increased degrees of restraint, a superposition of the global and local stresses and, at least in the area of the uninfluenced base material, an elastic behaviour is to be assumed. It should be noted that, in contrast to the free shrinking specimens, the surfaces of the slot specimens had to be cleaned by sandblasting in preparation for the milling of the seam preparation, which was followed by a stress-relieving annealing (60 min at 550 °C). The initial state of the residual stresses at the surface of the unwelded slot specimens made of S960QL in longitudinal and transverse direction is approx. −100 MPa. The resulting superimposed residual stress distribution thus shows increased transverse residual stresses in the area of the HAZ and the base material compared to the free shrinkage welded specimen, cf. Fig. 10a. Compared to P2, the increase in the restraint intensity from 10 kN/(mm mm) to 20 kN/(mm mm) causes an increase in these reaction stresses from about 100 to 150 MPa in the BM and from about 150 to 200 MPa in the HAZ. Further away from the weld (y=100 mm), the tensile residual stresses approach the initial state of approx. −100 MPa again.

In the longitudinal direction, the tensile residual stress maxima in the weld metal of the free shrinkage specimen, cf. Fig. 10c, are located at a distance of about 2 mm to 4 mm from the weld transition to the HAZ and amount to approx. 450 MPa in the case of the first welded cap bead and over 300 MPa in the case of the last welded cap bead. Secondary maxima occur at a distance of a few millimetres from the centre line of up to over 150 MPa for the last welded cap bead and up to 300 MPa for the first welded cap bead. The areas of the centre lines of the cap beads as well as the transition between the two cap beads are characterised by dips in the longitudinal residual stress profile, which is characteristic for transformable steels. In the further course from the HAZ towards the base material, the residual stresses drop into the negative range due to compensating compressive residual stresses or to the initial surface residual stress state, respectively.

Both materials show a significant increase in transverse residual stresses, especially in the HAZ and in the BM, which are caused by an increase in the restraint intensity in the transverse direction of the weld. Figure 11 illustrates this by comparing the values of all measured transverse residual stresses on all tested weld specimens (P1 to P3) for both steel grades as a function of the restraint intensity. It should be noted that in addition to the representation of the residual stress maximum values, residual stress levels are also represented. For the calculation of such levels, the average transverse tensile residual stresses in the corresponding areas, such as weld metal (WM), heat affected zone (HAZ) and base metal (BM), was calculated according to eq. 2. For the values y, the weld transition (weld metal to HAZ) or the transition from the HAZ to the base metal (typically approx. 10 mm width) was used in each case [26].

$${\sigma}_{y,m}^{rs}\left({y}_1\dots {y}_2\right)=\left(1/\left({y}_2-{y}_1\right)\right)\int_{y_1}^{y_2}{\sigma}_y^{rs}(y) dy$$
(2)
Fig. 11
figure 11

Values of transverse residual stresses for different weld zones vs. restraint intensity for both steel grades

Full size image

All values for the residual stress maxima and residual stress levels in Fig. 11 increase with higher restraint intensity. In the base material, the residual stresses increase to an average value of 140 MPa for both materials due to the reaction stresses resulting from shrinkage restraint by the slot specimens. On average, the maximum transverse residual stresses increase by approx. 100 MPa at the highest restraint. For the material S500MLO/G50, the transverse residual stresses in the HAZ are slightly higher than for the material S960QL/G89, especially at higher restraints. This is since the diverse materials and filler metals (S500MLO/G50 compared to S960QL/G89) cause a different transformation behaviour due to different alloy contents and partially due to the different welding heat control as a result of higher heat input and interpass temperature when welding S500MLO/G50. Regarding both the level and the maximum transverse residual stresses in the WM, the increase of the restraint intensity to 20 kN/(mm.mm) causes an increase of about 100 MPa on average. It is worth noting here that the significantly higher strength weld metal of G89 has more than twice the transverse residual stress maxima compared to the G50 (nominal Rp0.2 according to the standard 890 MPa compared to 500 MPa) and about 100 to 150 MPa higher transverse residual stress levels depending on the restraint intensity.

4.3 Cold cracking

The restraint intensity of the welded slot specimens has an increasing effect on cold cracking, especially in the case of high-strength steel grades with low strain reserves due to the expected mechanical stresses introduced by the welding process. Cold cracks are intercrystalline or transcrystalline material separations and form during or after welding in the HAZ or WM. Cold cracks are the result of a critical interaction between microstructure, mechanical stress and hydrogen concentration in the weld area and occur after cooling below 200 °C up to several days after welding [27]. The risk of cold cracking is exemplified experimentally at this point, as cold cracking is a common cause of weld repairs. In this context, it was possible in some experiments to purposely provoke cold cracks on slot specimens due to welding. This cold cracking provocation was realised by adding water-based anti-spatter spray to the MAG torch prior to welding the filler and cap layers. It can be seen, cf. Fig. 12a, that on the one hand the S500MLO or G50 is not susceptible to cold cracking. Even with the highest mechanical welding stresses in the slot specimens (residual stresses up to the material strength), no cold cracks could be detected in the radiographic testing of the welds independent of the restraint intensity. In contrast, the high-strength quenched and tempered steel S960QL or filler metal G89 shows a higher susceptibility to cold cracking, cf. Fig. 12b and c.

Fig. 12
figure 12

Radiographic examination of welded specimens with or without hydrogen introduction during welding for both steel grades: a S500MLO/G50, b S960QL/G89; c macrosection and detail of a crack in WM of S960QL/G89 with medium restraint intensity (P2)

Full size image

It is noteworthy that the peripheral stiffness in the longitudinal direction is already sufficient for free shrinking specimens that transverse cracks occur in all specimen shapes made of S960QL/G89. With increasing restraint intensity of the specimens transverse to the weld, during welding, the number and length of the cracks increase in the welding direction. For welding without additional hydrogen introduction (no use of anti-spatter spray), all welds of S960QL/G89 are crack free independent of the restraint intensity of the specimens.

5 Conclusions

For repair welding, comprehensive investigations are required, especially for high-strength fine-grained structural steels due to their special microstructure and limited strain reserves, in order to develop adequate scientifically based repair concepts for standardisation recommendations. To date, this has only been done inadequately or primarily for low-strength steels. As high shrinkage restraints are to be assumed for repair welding on larger components or assemblies, these must also be represented in experiments.

  1. (i)

    Numerical investigations on an actual assembly group of a mobile crane and on near-component slot specimens show high restraint intensities, which depend on the length of the slot representing the gouge length in repair welding. The restraint intensity values found were confirmed by experimental restraint analyses.

  2. (ii)

    Welding causes a significant increase of the total transverse residual stress level over the entire seam area with increasing shrinkage restraint of the weld.

  3. (iii)

    As in higher strength steel grades S960QL/G89 a higher stress level in the weld metal is observed, in lower strength offshore steel grades S500MLO/G50 higher peak stresses in the HAZ can be found. In the base metal of the weld vicinity comparable stress levels due to restraint shrinkage of the specimens are evident.

  4. (iv)

    Higher strength steel grades like S960QL/G89 show a distinct higher cold cracking risk. Experiments with an additional hydrogen source during welding (water based anti-spatter spray) showed cold cracks in all specimens, with increasing number and length of the cracks at higher restraint intensities. No cracks were found, for the weld test without hydrogen. The offshore steel grades S500MLO/G50 did not show any cracking independent of restraint conditions and hydrogen introduction.

  5. (v)

    From that it can be recommended that all kind of hydrogen sources should be avoided, especially for high strength-steels. Therefore, all procedures before and during welding and the use of welding auxiliaries should be carefully considered.

  6. (vi)

    Furthermore, an appropriate selection of the repair strategy is required including measures for disassembly preliminary to repair welding to decrease restraint intensities and unnecessary welding stress increases.

  7. (vii)

    There is also the possibility—especially if restraint intensity cannot be further reduced—to minimise local and global welding stresses and avoid critical microstructure by means of optimal adapted heat control during repair welding, which will be focussed on in part 2 of this investigation [1].