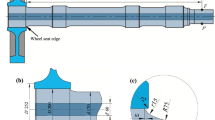
Abstract
Freight wagons primarily consist of welded steel structures subjected to time varying loads. Therefore, fatigue associated with the welding process is a common failure mode. Several technical codes for fatigue assessment have been proposed, being DVS 1612–2014 and ERRI B 12/RP 60 two of the most used. Nevertheless, no clear correlation between both codes is yet found in the bibliography. To overcome this, the present paper develops a full comparison over a study case of a freight wagon frame model. Finite element method is used for the stress calculation based on loads according to UNE-EN 12663-2. Weld performances comply with UNE-EN 15085-3. Fatigue post-processing is carried in parallel using DVS and ERRI codes. Finally, fatigue results of both codes are compared at each element of the model and each weld type. The results obtained provide a complete overview of the influence on the fatigue design of choosing a specific technical code for fatigue assessment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Wagon frames consist of several steel components welded together. Since welded joints result in stress concentration areas [1], these zones are prone to fatigue failure. Besides that, fatigue failure can take place in a sudden way, since it is not always possible to monitor the crack growth accurately, thus making it an important safety concern within railway industry [2]. Due to this, fatigue strength evaluation in wagon frames is a decisive part of rolling stock design, for which several technical codes have been developed with the objective of minimizing the failure in welded wagon frames during operation. Among them, DVS 1612–2014 [3] and ERRI B 12/RP 60 [4] (or UIC B 12/RP 17 [5]) can be highlighted as two of the most widely accepted and utilized within railway industry over the last decades. Nevertheless, there is no unification of both codes up to date; being both accepted for fatigue calculation. In spite of the fact that both technical codes are valid for fatigue strength assessment, there is limited information explaining the comparative characteristics and differences between them. In this regard, Slavchev et al. [6] performed a comparison of both technical codes but focusing on bogie frames, where they concluded that the same areas of insufficient dynamic strength are obtained with both codes, with no further analysis of the differences obtained. Similarly, Stoilov V. et al. [7] provided equivalent results over a freight wagon frame but limited to unsigned Von Mises stresses with its inherent deviation from real stress cycle for fatigue evaluation. However, it was concluded that DVS allows for a more precise notch case selection due to higher number of notch case curves allowing thus to obtain higher safety factors.
To overcome the lack of convergence between both technical codes, the work presented in this paper aims to perform a detailed comparison of both technical codes over the same freight wagon frame model in combination with the finite element method (FEM). The general design of the frame is performed following the current tendencies of wagon design for transportation of goods. Also, a wide variety of types of welds are employed in the frame in order to ensure a complete comparison between both DVS and ERRI codes. The input loads introduced on the FEM model to simulate normal operation of the wagon during its life span correspond to the ones defined in the standard UNE-EN 12663-2 [8] which contain a total of four different load cases based on inertial acceleration levels in vertical and lateral directions.
The stress results obtained on the FEM model for each load case are subsequently post processed for fatigue evaluation according to DVS and ERRI technical codes in parallel. The ultimate fatigue assessment indicator output by both codes is the so-called Usage Factor (UF), which relates the stress suffered by an element with the maximum admissible value that ensures infinite fatigue life. The UF is obtained for each element of the FEM model, and is the value utilized in this work for comparison purposed between both codes.
Detailed comparative results obtained for different types of welds, weld heat affected zones (HAZ), and base metal are presented in the results section of the article. In all, the findings of this work provide valuable information for the design of wagon frame structures, supplying a global view of the implications of choosing one code or the other for the fatigue assessment.
2 Theoretical basis of DVS and ERRI technical codes
The following subsections will introduce the basis of both technical codes, as well as a comparison of the permissible limits between them. It should be noted that only the general characteristics of these codes are brought here, for a detailed explanation, the reader should refer to the original texts [3, 4], and [5].
2.1 DVS 1612–2014 [3]
Technical code DVS 1612 defines maximum admissible stress as a function of the stress ratio “R,” which is defined as the quotient between the minimum stress “\(\sigma _{min}\)” and maximum stress “\(\sigma _{max}\)” of the fatigue cycle, as shown in Eq. 1:
The curves that define maximum admissible stresses are referred by the technical code as “notch case lines” and are divided into normal, longitudinal and shear stresses in the plane of the joint, as shown in Fig. 1.
In this sense, for longitudinal and normal stresses, the admissible values are defined in Eqs. 2 and 3 for tensile and compressive mean stresses respectively. Note that the compressive stress ratio factor “k” introduced in Eq. 3 is the inverse of the stress ratio defined in Eq. 1. Finally for the shear stress, admissible value “\(\tau _{zul}\)” is governed by Eq. 4.
The exponent “x” in Eqs. 2 and 3 and value “\(\tau _{zul,R=-1}\)” in Eq. 4 are dependent of the notch case line selected. These notch case lines are classified based on different parameters such as geometry of the joint, type of weld and weld performance class according to UNE-EN 15085-3 [9].
Critical plane method. From left to right: determination of \(\sigma _{max}\), determination of \(\sigma _{min}\) and resulting fatigue cycle. Where \(\sigma _1\),\(\sigma _2\),\(\sigma _3\) are the principal stresses and \(\alpha \) the angle with respect to the reference Cartesian coordinate system
Table 1 summarizes notch cases for DVS technical code, based on metal condition (base metal, thermally influenced metal or welded joint). It should be noted that for each stress direction, the notch case lines follow a descending alphabetical order. Being the “A+” the notch case line with the highest resistance associated, and the “F3” with the lowest. Similarly, for shear stresses, notch case line “G+” has the highest admissible value and “H-” the lowest. As shown in this table, highest resistance notch case lines are reserved for base metal and thermally influenced areas regardless the stress direction.
Admissible limits defined in Eqs. 2, 3, and 4, are represented graphically in the technical code by means of the so-called MKJ diagrams, which relate, maximum stress of the fatigue cycle “\(\sigma _{max}\),” as a function of the stress ratio “R.” By way of example, Fig. 2 shows such diagram for longitudinal loads, where the admissible values for the different notch case lines are plotted. For shake of clarity, only main categories letters are plotted over the limit curves.
Initially, MKJ diagrams apply for a thickness range from 2 to 10 mm. For thicker plates, fatigue strength is progressively reduced. For tensile and compressive stresses, maximum admissible values should never exceed the yield strength of the material. For shear stresses, its maximum admissible value should never exceed the yield strength divided by \(\sqrt{3}\). It should be noted that that admissible limits are higher for compressive stresses.
Infinite fatigue life with a survival probability of 99.5% is ensured when all 3 stress components are lower than admissible value “\(\sigma _{zul}\)”:
Furthermore, if an element exhibits more than one non negligible stress component, fatigue strength is also subjected to:
Equations 5 and 6 express the usage factor (UF). While these factors are lower or equal to 1 for Eq. 5 and 1.1 for Eq. 6, infinite fatigue life can be ensured within the confidence level stablished by the technical code.
2.2 ERRI B 12/RP 60 - Goodman diagram method [4]
ERRI B 12/RP 60 technical code offers two different methods for analyzing fatigue strength, cumulative fatigue summation method and Goodman diagram method. For this research the Goodman diagram method is chosen since it provides an evaluation with respect to infinite fatigue life and therefore can be compared with DVS 1612 technical code. Further references to ERRI technical code will therefore refer to Goodman method.
This code employs the critical plane method to obtain the fatigue cycle from different load states (Fig. 3), which can be summarized in the following steps:
-
Determination of principal stresses and directions for every load case.
-
Location of the highest principal stress, which will correspond to “\(\sigma _{max}\).”
-
Projection of the stress tensors of the rest load cases over the “\(\sigma _{max}\)” direction.
-
Lowest projected stress will correspond to “\(\sigma _{min}\).”
Admissible limits are defined based on the well known Haigh diagrams, which sets admissible boundaries for the stress range “\(\sigma _{2a}\)” as a function of mean stress “\(\sigma _{m}\)”:
ERRI technical code expresses the maximum admissible values in 5 different categories attending to the geometry of the joint as follows:
-
A - Parent metal
-
B - Butt weld
-
C - Butt weld with inertia change
-
D - Filet weld
-
E - Projection weld
The admissible limits for these categories are plotted in Fig. 4. ERRI technical code assumes that the admissible stress range is independent of mean stress since wagon frames do not undergo stress relaxation treatments. However, maximum admissible value is ultimately limited by yield strength. To facilitate the comparison, tensile, and compressive means tress zones are highlighted in blue and red color respectively in accordance to the color code used in Fig. 2.
Infinite fatigue life is ensured within a survival probability of 99.7% when the stress range is lower than the admissible value:
Equation 9 is known as usage factor (UF) for ERRI technical code. While the usage factor is lower or equal than 1, infinite fatigue life can me ensured with the confidence level established by the technical code.
2.3 Comparison between MKJ and haigh diagrams
As observed in previous Sects. 2.1 and 2.2, both codes aim to usage factor calculation, whose value is the comparative base of this study. It is important to highlight that both codes are based in nominal stress evaluation, and as such, they do not account for local effects due to geometry change at the vicinity of the weld for the stress calculations. This approach is the most extended within railway industry since it is aligned with the common modeling techniques of FEM models for wagon frame structures.
Although both technical codes use different diagrams to represent the maximum admissible limits (i.e., MKJ for DVS and Haigh for ERRI), both contain the same information. For this reason, it is straightforward to switch from one representation to the other for comparison purposes. For the current analysis, ERRI Haigh diagrams are expressed as MKJ diagrams. Figure 5 shows admissible limits for both technical codes for S355 steel, which is commonly used for wagon and bogie frame construction [6, 7], and [12].
As observed in Fig. 5, several aspects can be noted:
-
Wider range of admissible limits is observed for DVS. Allowing in general a more precise category selection for the different junctions.
-
Tensile mean stresses: ERRI becomes less restrictive as the stress ratio increases with respect to DVS.
-
Compressive stress curves follow the same tendency irrespectively of the technical code. Even coincident curves are noted for A* - E1 and C* - F2.
-
In general, admissible limits for ERRI seem to be lower for equivalent categories. For example, A category in ERRI, reserved for base metal, coincides with E1 category in DVS, which is employed for some types of welds.
Finally, it should be kept in mind that fatigue assessment based on these technical codes is not only dependent on its stress admissible limits, but also on the method used for fatigue cycle calculation as described in Sects. 2.1 and 2.2 (i.e., components evaluation for DVS and critical plane method for ERRI). The resulting stresses to be evaluated against admissible limits in order to obtain the final UFs are different, and a comparison of both methods based only on these admissible limits curves is incomplete.
Therefore, a complete comparison about usage factors obtained by both technical codes should be performed also including stresses results processing from a FEM model. For this purpose, a dummy wagon model will be employed in the present article as described in the following sections.
3 Description of the wagon model
For this study, the wagon frame model subjected to study is built and calculated using the finite element method (FEM), well known and widely used by railway industry for stress calculations. In this case, the software used for wagon frame design and finite element analysis is Ansys Workbench. Although the frame does not correspond to a real application, it is based on a wagon used for general purpose goods transportation. A general overview can be seen in Fig. 6. It is composed of two main solebars at each side and a central solebar between frame bolsters. Four transverse beams connecting each lateral solebar with one central longitudinal beam provide proper structure of the central part of the frame. Finally, headstocks are connected to the main bolsters via the solebars and four stanchions. The frame is symmetrical with respect to its longitudinal and transversal axis. Steel plate thickness range from 10 to 30 mm and the construction material is structural steel S355 J2 with a Poisson ratio of 0.3, a Young modulus of 210 GPa and a yield strength of 355 N/mm\(^2\) for thicknesses less than 16 mm and 345 N/mm\(^2\) for thicknesses greater or equal to 16 mm according to EN 10025-2 [10].
Welding design and execution of the frame complies with UNE-EN 15085 standard, as one of the requirements from the technical codes to rely on the specified admissible stress limits. The different welds assigned to the model junctions are based on real life examples for similar joints. As observed in Fig. 7, different butt joints and T-joints with partial or full penetration are used with the purpose of covering a complete range of weld types in the comparison [11].
The model was meshed using 4-node shell element type (identified as Shell 181 in Ansys element library). Using a target element size of 20 mm, the total number of elements was 118,624. This type of element is widely used in railway industry [12] and recommended for sheet plates geometries, where one of the dimensions (thickness) is much smaller with respect to the other two, since it provides accurate enough results while maintaining relatively low computing costs. In this sense, DVS and ERRI technical codes are based in nominal stress methods, therefore FE weld modeling is not necessary, since stress concentrations and mechanical properties variations due to welds are considered in the aforementioned curves. Consequently, all mesh elements have the mechanical properties described in Sect. 3, which correspond to base metal, and the stress values obtained at each element will be used for the fatigue post processing.
In relation with the above, elements of the model adjacent to joining edges are considered as weld elements, whereas the adjacent correspond to the heat affected zone (HAZ) [13]. Finally, the remaining elements are considered as base metal of the frame. For better understanding, Fig. 8 shows an example of the element classification on a simple T-joint.
In order to stablish the admissible values for each joint, weld categorization according to each technical code is needed and will be described in more detail in the following section.
The loads applied to the wagon frame are according to the requirements of the standard UNE-EN 12663-2, which establishes the loads to be considered in this type of vehicles. Among all load cases described in this standard, those defined in tables 13 and 14 are used for fatigue study. In this sense, these tables relate the inertial accelerations that are induced by the track to the wagon during operation, where lateral accelerations (\(a_y\)) are defined in table 13 and vertical accelerations (\(a_z\)) in table 14. A total of four load cases are obtained by combining the values defined in these tables, as summarized in Table 2.
With respect to the boundary conditions, the set of axes chosen is described in UNE-EN 12663-2 and illustrated in Fig. 9. The constraints are applied to the model in order to simulate the support of the frame on the center pivots and side bearers. For simulating the center pivots, a remote point constraint is used. If assumed that the center pivot is non deformable, the wagon frame will freely rotate around its sphere center. Therefore, displacements along y and z axes are limited, whereas displacement along x axis is only limited to one center pivot to avoid rigid body motion and ensure proper model convergence.
For simulating the supporting effect of side bearers, displacements along z axis are limited. Load cases must be taken into account, since they will determine which pair of side bearers will limit wagon roll due to non-compensated lateral inertial accelerations (Fig. 9).
Once the model has been properly meshed and the loads and boundary conditions defined, it can be considered ready for solving. The resulting element stress tensors at each side of each element of the model will be employed for the subsequent fatigue post processing.
3.1 Weld categorization
As commented above, weld resistance is established for both codes depending on different categories. Thus, it is necessary to relate each weld type of the model with a specific category for both DVS and ERRI codes. Although a deep explanation of the criteria underlying the weld categorization process is out of the scope of this work, Table 3 describes the categories utilized for each type of weld of the frame model presented in Fig. 7.
It is first noted that DVS makes distinction on the categories depending on the stress components acting on the weld. Additionally, for T-type joints, different resistances are also assigned for web and chord plates of the junction.
Additionally, from the observation of the MKJ diagrams presented in Fig. 5 for both codes, it is noted that categories associated with more restrictive limits are prescribed in ERRI codes, and thus more conservative results might be expected. However, as stated in Sects. 2.1 and 2.2, is important to remind that comparison is not straightforward, since fatigue strength is not only related to admissible limits, but also on the stress cycles obtained from the stress results, which are different for DVS and ERRI codes.
3.2 Fatigue post processing
Regarding the DVS technical code, fatigue post processing for each element is schematized in the flowchart of Fig. 10. First, the stress results obtained for each element face are expressed in the three stress components mentioned in Sect. 2.1. Maximum and minimum stress values for each stress component will define a fatigue cycle for each element. Later, the stress ratio will be calculated along with its corresponding maximum admissible value based on MKJ diagrams and the corresponding notch case line. A total of four usage factors are obtained at every element side of the model, corresponding to the four relations presented in Eqs. 5 and 6. The maximum usage factor will be considered as the representative one for comparison purposes, since is the one that will determine fatigue failure.
For ERRI technical code, fatigue post processing for each element of the model is computed as described in Fig. 11. Once stress results for each element face are expressed in the principal directions, the fatigue cycle is obtained following the critical plane method as summarized in Sect. 2.2. Then, mean stress and stress range are directly obtained according to Eqs. 7 and 8. For the mean stress, maximum admissible stress range can be obtained considering the geometry of the joint as described in Sect. 2.2. Finally, the usage factor can be calculated as stated in Eq. 9. Since ERRI code does not work with stress components independently, but with principal directions, only one usage factor is calculated at each element side, corresponding to the principal direction of the maximum stress.
4 Results
The usage factors obtained as described in the previous section are scalar values associated to each element, and as such they can be plotted directly over the FEM model. This allows to analyze most solicited areas in term of fatigue over the wagon frame design. For example, Fig. 12 shows a general overview of the maximum UF values for the complete wagon frame for both DVS and ERRI. Figure 13 shows the same results focused on the most solicited zone, which corresponds to the lower side of the frame bolster. It can be noted that on average, DVS usage factors tend to be lower than ERRI usage factors. Maximum usage factor for DVS technical code is 0.69, whereas for ERRI technical code is 0.87. It should be noted that both methods place the highest usage factor in the same element.
As expected, base metal and heat affected zones exhibit in general lower usage factors than welded joints. This is due to the location of these elements, far enough from notch effects and to the higher fatigue resistance associated to these areas.
In Fig. 14, a comparison between the usage factors of both technical codes can be observed. Elements with lower usage factor for DVS technical code are shown on blue, whereas the ones with lower usage factor for ERRI are colored in red. In general terms, welded elements show a lower usage factor when DVS method is applied, in contrast with base metal and heat affected zones, where there is not a clear trend over the conservative nature of one technical code over the other.
In order to supply a detailed comparison on the weld types, the following subsections investigates deeper the differences between technical codes of every joint type.
4.1 Full penetration butt welds
Butt welds are employed when two plates are welded end to end without overlapping each other. They are commonly used in wagon frames to join the different bottom flanges of the main solebars or the flange of the solebars and stanchions to the frame bolster. When fatigue stresses act on this welds, full penetration welds are recommended.
Two types of full penetration welds are used in the example wagon:
-
Two sided butt weld: weld type 2c according to EN 15085, categorized as E1 (\(\sigma _{//}\)), E1 (\(\sigma _{\perp }\)) and G (\(\tau \)) for DVS, and C for ERRI (see Table 3). Weld numbers 17, 18, 22, and 23 are of this type in the wagon, and the highest UF obtained for each are summarized in Table 4. Is it noted that for welds 18, 22, and 23 ERRI code is more conservative. The exception of weld 17 is found due to an element of the weld which is shared with weld No.7 (partial penetration angle weld, type 13b) as shown in Fig. 15. As such, this element will also share the corresponding categorization to 13b weld, which is more restrictive. Further study of this point is found in Sect. 4.3.
-
One side butt weld: weld type 3a according to EN 15085, categorized as E1- (\(\sigma _{//}\)), E1- (\(\sigma _{\perp }\)) and G (\(\tau \)) for DVS, and C for ERRI (see Table 3). Weld numbers 8, 15, and 19 are of this type in the wagon. The highest UF obtained for each weld are summarized in Table 5, where is noticed that all welds ERRI code shows more conservative results.
4.2 Full penetration T joints
T joint types are employed when two plates that are in angle, usually at \(90^{\circ }\), need to be welded. Additionally, full penetration welds are applied when partial penetration welds do not achieve sufficient mechanical resistance. This type of welds are frequently used in wagon frames to join stanchions or solebars to perpendicular surfaces such as the frame bolster web or the headstock.
Two types of full penetration T type welds are used in the example wagon:
-
Two sided T-joint: weld type 10b according to EN 15085, categorized as C- (\(\sigma _{//}\)), E5/E5 (\(\sigma _{\perp }\), chord/web) and H+ (\(\tau \)) for DVS, and D for ERRI (see Table 3). Weld numbers 1, 3, 4, 10, 11, 20, and 21 are of this type in the wagon. The highest UF values obtained for each weld is shown in Table 6. Again, UF are lower for DVS code, with the exception weld 21. This weld is probably subjected to several non-negligible stress components, where the DVS usage factor is determined by Eq. 6.
-
One sided T-joint: weld type 10a according to EN 15085, categorized as C- (\(\sigma _{//}\)), E6+/E6- (\(\sigma _{\perp }\), chord/web) and H+ (\(\tau \)) for DVS, and D for ERRI (see Table 3). Welds no. 2, 9, 12, 13, and 14 are one side butt weld in the wagon. The highest UF values obtained for each weld is shown in Table 7. With no exception, all UF are lower for DVS code in this type of welds.
4.3 Partial penetration T joints
Partial penetration T-joint types are employed to weld angle plates where mechanical resistance in not so demanding and thus full penetration is not required. They are generally used on frame wagons to connect the reinforcing stanchions between the lateral and central solebars. Additionally, they are also used in the connection between the web and flanges of aforementioned solebars.
Is a weld type 13b according to EN 15085, and is categorized as C- (\(\sigma _{//}\)), E5/F2 (\(\sigma _{\perp }\), chord/web) and H (\(\tau \)) for DVS, and D for ERRI (see Table 3). It is noted that while ERRI makes no category distinction between full and partial penetration T-joints, DVS significantly lowers the category of the later for stresses perpendicular to the weld when the web is loaded. It should be pointed out that ultimately, D category in ERRI and F2 in DVS, meaning the ERRI code sets similar admissible stresses as the worst loading case of DVS. Due to this, the conservative tendency of one code over the other might vary depending on the type of loading on the weld elements.
Weld numbers 5, 6, 7, and 16 are of this type in the wagon. The highest UF obtained for each of these welds is summarized in Table 8, where it is confirmed the general conservative tendency of ERRI over DVS code. It is also noted that the differences between both codes varies significantly depending on the weld, which confirms the influence of the load dependent categorization of DVS, being especially notable for this type of weld.
5 Conclusion
In the present work, a detailed comparison between the two most utilized codes for fatigue analysis of freight wagon frames has been developed, analyzing the different welded joints configurations that can be found in a common wagon frame design.
The analysis was carried out on the basis of a wagon frame FEM model frame employed as an example for this purpose. Fatigue loads introduced on the model are in accordance with the requirements of UNE-EN 12663. This standard, based in proven experimental data, allows to calculate fatigue cycles during the lifespan of the wagon. The data provided by this standard allows for fatigue strength verification based on theoretical models, and as such it does not exempt from real life fatigue tests. However, it is sufficient to understand the differences between ERRI B 12/RP 60 and DVS 1612 technical codes.
Both ERRI B 12/RP 60 and DVS 161 codes provide a methodology for fatigue assessment of welded wagon frames, based on the so called nominal stress approach. They each propose stress post-processing methods together with admissible stress limits based on weld categorization. It was shown that the inherent differences between both codes impedes to perform a straightforward comparison based only on the stress limit curves.
Results obtained over the example wagon frame showed that the technical code DVS 1612 is in general terms less conservative than ERRI B 12/RP 60 for weld assessment. This tendency is not so clear for HAZ and base metal as noted in Fig. 14, but these areas are rarely the critical ones fatigue assessment of freight wagons
Despite of the different methods used for fatigue cycle calculation, DVS technical code provides a more exhaustive categorization for welded joints. Therefore, more fidelity in notch case election is achieved. Additionally, it is remarkable the assumption carried out by ERRI technical code about the null effect of mean stresses over the stress range. This simplification probably have contributed to more conservative results for compressive mean stresses. It was observed in the comparative results by weld type that for most cases the DVS code predicted lower usage factors. Only two exceptions were found corresponding to very low values, where relative non negligible multiaxial states might take place for such low stresses, which are specifically accounted in DVS as shown in Eq. 6.
It should be also considered that ERRI B 12/RP 60 is easier to handle, given the simpler notch case division, as well as the stresses post processing, where just one usage factor per element side has to be obtained.
In all, the results provided in this article suppose a valuable information for the design of freight wagon structures, giving a general view of the implications of selecting DVS 1612 of ERRI B12/RP60 for fatigue assessment.
References
Fernández JÁP (2017) Theoretical and experimental study of the fatigue behaviour of large passenger transport vehicles under dynamic operating loads. Universidad Politécnica de Madrid, Madrid
Niu CL, Xie SM, Wang W (2019) Stress state grade evaluation method for welded joints of complex structures on railway rolling stock and its application in welded frame. Dailan: School of Locomotive and Rolling stock Engineering, Dailan Jiaotong University
DVS, Technical Comittee, Working Group (2014) ‘Welding in railway vehicle manufacturing’. Technical Code DVS 1612. Design and endurance strength analysis of steel welded joints in rail-vehicle construction. DVS - German Welding Society
ERRI (2001) ERRI B 12/RP 60 - 2ND Edition. Tests to demonstrate the strength of railway vehicles. Regulations for proof tests and maximum permissible stresses. ERRI (European Rail Research Institute)
UIC (2012) UIC B 12/RP 17 9th Edition. WAGONS. Programme of tests to be carried out on wagons with steel under frame and body structure (suitable for being fitted with the automatic buffing and draw coupler) and on their cast steel frame bogies. UIC (International Union of Railways)
Slavchev S, Maznichki V, Stoilov V, Enev S, Purgic S (2018) Comparative analysis of fatigue strength of an Y25LS-K bogie frame by methods of UIC and DVS 1612. Czech Republic
Stoilov V, Slavchev S, Purgic S (2014) Study of fatigue in welded joints and stress notches of wagon. Technical University of Sofia, Faculty of Transport, Sofía
AENOR (2011) UNE-EN 12663-2. Aplicaciones ferroviarias. Requisitos estructurales de las cajas de los vehículos ferroviarios. Parte 2: Vagones de mercancías. AENOR, Madrid
AENOR (2008) UNE-EN 15085-3. Aplicaciones ferroviarias. Soldeo de vehículos y de componentes ferroviarios. Parte 3: Requisitos de diseño. AENOR, Madrid
AENOR (2018) DIN EN 10025-2:2018-07. Hot rolled products of structural steels - Part 2: Technical delivery conditions for non-alloy structural steels
Bruno V (2021) Análisis comparativo de la resistencia a fatiga del bastidor de un vagon de carga por métodos numéricos: comparativa entre códigos técnicos DVS y ERRI. Escuela Politécnica de Ingeniería, Gijón
Milovanovic V, Živković MM et al (2014) Experimental and numerical strength analysis of wagon for transporting bulk material. GUniversity of Kragujevac, Faculty of Engineering
Sarmiento E (2022) Evaluación mediante ANSYS de la resistencia a fatiga de uniones soldadas en carrocerías de vehículos de transporte. Universidad Politécnica de Madrid, Madrid
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Recommended for publication by Commission XIII - Fatigue of Welded Components and Structures.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vega, B., Pérez, J.Á. Comparative analysis of fatigue strength of a freight wagon frame. Weld World 68, 321–332 (2024). https://doi.org/10.1007/s40194-023-01577-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40194-023-01577-5