1 Introduction

The appearance and increasing spread of weldable high-strength steels (HSS) can be explained by their numerous advantageous properties [1]. With the application of HSS, significant weight reduction and material saving can be achieved in engineering structures. However, their application raises some questions and therefore, ongoing research is focused on the applicable welding process window and the selection of optimal welding parameters and filler materials [2-4]. Some decades ago, the application of overmatching filler materials was the generally accepted approach in the course of design and production of welded structure, which ensured the strain concentration was primarily on the base material and other elements beyond the weld during loading. With the spreading application of HSS, it has become necessary to widen the application field of consumables; therefore, matching and undermatching filler materials have become commonly used in the higher strength categories of structural steels [5-7].

While the strength design can be performed with sufficient safety in the case of welded structures at static loading conditions, damage resulting as the effect of cyclic loading is difficult to predict at matching and undermatching welds. Therefore, the availability of the necessary material characteristics for the design calculations is limited [8, 9]. This is especially true for low-cycle fatigue (LCF), where local plastic strain may occur due to the different stress levels and/or material properties at certain volumes of the structure (e.g., in the surrounding of notches and material discontinuities) [10]. Considering that the microstructure of high-strength steels is far from the equilibrium state due to the demanded yield strength, significant microstructural changes and thus the variation of mechanical properties can be expected as the effect of welding heat cycles [4, 11]. This further complicates the fatigue design and demands a new approach to the determination of material characteristics.

The aim of the present research is to investigate the effect of two quenched and tempered steel grades (S690QL and S960QL) including their weldability and the filler material selection on the LCF behavior of differently matched welded joints. In the case of S690QL, the LCF resistance of matched and overmatched gas metal arc welded (GMAW) joints is analyzed, while at S960QL, matched and undermatched conditions are examined. Based on the experimental work, a recommendation can be provided for the proper filler material selection strategy (mismatch) at the two high-strength steel grades concerning low-cycle fatigue loading.

2 Weldability of HSS

These high-strength steels generally have a fine-grained tempered martensitic and/or bainitic microstructure as the result of the chemical composition and the special rolling and heat treating technology [4, 11]. However, the precisely optimized non-equilibrium microstructure by the steel producers is irreversibly changed due to the welding heat input. The heat-affected zone (HAZ) can be either hardened or softened in the function of steel grade and welding parameters; furthermore, the toughness properties can drastically decrease in the coarse-grained and the intercritical subzones. In the case of multipass welding, the structure of the evolved HAZ is more complex, resulting in local brittle zones (LBZ) where the unfavorable characteristics of the different subzones meet. To reach the acceptable strength and toughness level in the HAZ, a variety of microalloying elements (Nb, Ti, V, Al) are applied, which have diverse effects on the mechanical properties [4]. The dendritic microstructure of the weld metal is far from the original fine grain structure and there is no industrially applicable post-weld heat treatment that can restore the microstructure of the base material. Besides the (quasi)static material characteristics, the microstructural changes in the welded joint have also a significant effect on the fatigue properties.

Beyond the reduction of mechanical properties in the weld metal and the further undesirable phenomena in the HAZ, the formation of different crack types (e.g., cold cracks) can appear. Primarily, to avoid cold cracking, the workpiece must be preheated before the welding, and it is necessary to limit the welding heat input (Q) [12]. The crack sensitivity of high-strength steels is illustrated in the Graville diagram (Fig. 1), based on the carbon content and the carbon equivalent (CEGraville). In the figure, the locations of the different steel grades were determined based on the 3.1-type base material certificates according to EN 10204 [13]. It can be clearly seen that the examined high-strength steels are in the hardest weldable category (III), which means that these steels should be welded with preheating and controlled heat input. Furthermore, with increase of the strength category, the weldability properties decrease.

Fig. 1
figure 1

Graville diagram [12]

Full size image

In the case of high-strength steels, the heat input control is generally a key to their successful welding. If the heat input is too low, the cooling rate of the welded joint may be too high, and then, cold cracks may occur depending in the steel grade. In the opposite case when high heat input is applied, a wide HAZ can form with softened areas; furthermore, the toughness properties can drastically decrease. Therefore, a narrow welding process window is recommended for the welding of high-strength steels. Since there are multiple factors influencing the total heat input, the t8/5 cooling time concept is generally implemented for the common description of the welding conditions and parameters, including heat input and preheating (Tpre)/interpass temperature (Tinter). The t8/5 cooling time is chosen to characterize the temperature/time cycle of an individual weld run during welding and is the time taken, during cooling, for a weld run and its HAZ to pass through the temperature range from 800 to 500 °C [14]. This cooling within this temperature interval is determining in terms of the final microstructure and mechanical properties. Steel producers generally recommend a cooling time range for their products, which can be a very narrow interval in high-strength steels (as short as 5–15 s at S960QL compared to 3–60 s at S355J2), which can be often a challenge to the welder during manual welding. Furthermore, the different types of filler materials can influence these phenomena, especially in mismatch cases [15]. Based on our previous investigations, the required mechanical properties can be reached in an even narrower range, namely for the S690QL steels the t8/5 cooling time should be between 6 and 15 s, while for the S960QL steels, we recommend between 6 and 10 s [16]. The sensitivity to cold cracking can be characterized by the hardness. When applying higher strength materials, the HAZ tends to harden over a wider cooling time range [17]. The expected hardness value is connected to the production method (e.g., Q + T, TMCP) of the given steel grade and the chemical composition, especially the carbon content.

3 Selection of filler materials

When high-strength steels are used in welded structures, the selection of the filler material is a crucial point. It is necessary to consider that in terms of the examined steels—based on the ratio of the base material and the filler material mechanical properties—matching, overmatching, or undermatching filler materials can be applied. With matching filler materials, the mechanical properties (generally the yield strength) of the weld are equal or nearly the same as the base material. When undermatching material is used, the strength properties of the weld are lower than the base material properties, while in the case of overmatching, the strength properties of the weld are higher [5-7].

The mismatch phenomena can be represented not only by the mechanical properties, but with other properties as well, such as the transition temperature or the cracking sensitivity. However, for practical reasons, the interpretation of mismatch during welding is limited to the strength characteristics. According to this, the conception of relative undermatching (rum) can be implemented [18]. In the case of matching, it is very hard to equal all of the mechanical properties. This is due to the fact that the yield/tensile ratio (Y/T) for the base material is usually different (and generally smaller), than for the filler material.

Nowadays, the challenge for filler material producers is to develop welding consumables for HSS by the shared application of macro- and microalloying elements with the avoidance of excessive increase of the carbon equivalent, and thus by the minimization of weld crack sensitivity. For long time matching, filler materials were only available up to 960 MPa strength category; however, special filler materials were recently developed for the 1100 MPa grade, while certain steelworks already produce 1300-MPa steel grade. It can be seen that filler material producers generally experience a delay of several years (or even a decade), since their only option is the optimization of alloying elements, while steel producers can combine the production technology (e.g., TMCP) with the alloying elements.

In the case of high-strength steels, once the mismatch ratio has been determined, the HAZ structure should be also considered. HAZ softening (together with the weld metal strength) can be crucial in terms of the strength and fracture behavior of the whole joint, and therefore, it cannot be neglected during the structural integrity calculations. When the lowest strength zone of the HAZ is overlapped with a subzone of reduced toughness, the strain can be concentrated on this part of the HAZ for matching/overmatching type joints, where crack initiation and propagation can occur relatively suddenly. The situation can be opposite in direct quenched steel when the normalized zone generally softens; however, the toughness improves due to the fine grain size [19]. Therefore, undermatching filler materials cannot be suggested in this case since the dendritic weld microstructure is likely to have lower toughness and higher crack sensitivity than the fine-grained zone. In the case of other high-strength steels (e.g., Q + T) when the intercritical HAZ tends to soften, the application of a filler material with lower strength but higher ductility can be considered if the weld has acceptable toughness and lower crack sensitivity. Numerous factors (e.g., mismatch ratio, softening level) influence the strength of an HSLA (high-strength low-alloy) steel weld joint with a softened HAZ [20]. When investigating the applicability of undermatching filler materials, the size of the softened zone should be also taken into account, since even a significant hardness reduction can have a minimal effect on the load-bearing capacity of the whole joint when the size is limited [6].

In the case of hot rolled mild steels, equal or slightly higher strength filler materials are used. In high-strength steels, with yield strength over 600 MPa, it may be more beneficial to use undermatching filler materials. Of course, in that case, a lower strength welded joint is gained. Despite the lower strength, these filler materials may have many advantages, which can be effectively used. Such positive attributes are the higher toughness of the weld metal, the higher resistance against hydrogen cracking, and therefore the lower preheating temperature or the smaller residual stress in the welded joint [7]. Besides the mentioned benefits, the location of the welded joint in the structure should be also considered. In places where the joint is fully load-bearing, the strength of the joint should be equal to the base material strength. In that case, the higher yield strength of the welded joint is more beneficial than the slightly higher residual stress, the higher toughness, or the worse LCF properties. But in places where the loading is lower, undermatching filler materials can be used.

4 Welding experiments

4.1 Base materials

Two strength categories (S690QL and S960QL according to EN 10025–6 [21]) of Q + T steels of the same thickness (t = 15 mm) produced by the SSAB steel manufacturing company were selected for the experimental program which aimed to investigate the LCF behavior of differently matched HSS welded joints. The mechanical properties of the two base materials according to EN 10204 [13] 3.1 material certificates are summarized in Table 1, where the high (almost equal to 1) Rp0.2/Rm value of both grades should be emphasized. The question may arise whether the LCF results from S690QL and S960QL are comparable considering the application of the same strain amplitude to the different grades. Since both steels have the same production routes, applied by the same steel producer with nearly equal Rp0.2/Rm value (Table 1), therefore a comparative study of the LCF results is possible. The chemical compositions in weight percent are summarized in Table 2. Both alloys have low impurity levels. The higher strength steel is alloyed by more carbon and molybdenum. Regarding the microalloying elements, boron can be highlighted, which is used in both categories to improve the quenching properties.

Table 1 Mechanical properties of the investigated base materials
Full size table
Table 2 Chemical composition of the investigated base materials
Full size table

4.2 Filler materials

As discussed in the previous section, the selection of the filler material is a very complex task. For S690QL, matching and overmatching filler materials were tested, while for S960QL steel, matching and undermatching filler materials were examined. Investigating both mismatch cases on the same steel grade, while desirable, was not an option due to the limited availability of S960QL overmatching filler materials. The selected filler materials and their main mechanical properties are summarized in Table 3, while their chemical compositions can be seen in Table 4 (according to EN 10204 [13] 2.2 material certificates).

Table 3 Mechanical properties of the investigated filler materials
Full size table
Table 4 Chemical composition of the investigated filler materials
Full size table

The carbon equivalents related to the cold cracking sensitivity of the applied base and filler materials were calculated based on the equations in EN 1011–2 [14] and are presented in Table 5. The filler materials belonging to the same strength category indicate higher values despite their lower carbon content, which is a result of higher nickel and manganese content.

Table 5 Carbon equivalents (calculated according to EN 1011–2 [14]) of the base and filler materials
Full size table

4.3 Experimental details

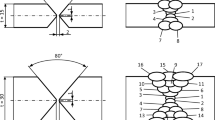
Gas metal arc welding (GMAW, ISO 4063 [22] code: 135) was chosen because these steels are frequently welded with this welding process [2, 4, 8]. Based on industrial experiences, M21 (according to EN 14175) mixed shielding gas with 18% CO2 and 82% Ar was chosen. As filler material, in the case of S690QL steel, THYSSEN UNION X85 (matching) and THYSSEN UNION X90 (overmatching) wire electrode were selected. In the case of S960QL steel, THYSSEN UNION X96 (matching coupling) and ESAB OK 14.03 (undermatching coupling) filler materials were chosen. The diameter of wire electrodes was 1.2 mm in all cases. For the experiments, a DAIHEIN VARSTROJ WELBEE P500L welding equipment was applied. To ensure uniform stress distribution, X joint preparation was designed according to Fig. 2, and the welded joint was regularly rotated during the multipass welding to reduce the weld distortion. The dimensions of the welded plates were 350 mm × 150 mm × 15 mm in accordance with EN ISO 15614–1 [23].

Fig. 2
figure 2

Joint preparation and welding order

Full size image

The root layers were made by a qualified welder, while the other layers were made by an automated welding car. The crucial welding parameters were selected to hold the cooling time between 6 and 10 s for S960QL and 6 and 15 s for S690QL depending on the steel grade. The welding parameters were continuously recorded during the experiments by a HKS welding monitoring system. The welding heat input was between 800 and 1100 J/mm. The applied welding parameters can be seen in Table 6, which summarizes the current (I), the voltage (U), and the welding speed (v) values, also the preheating (Tp) and the interpass (Ti) temperatures, with the heat input and the calculated cooling time (t8/5) values. The parameters of the root and the filler passes are presented separately in each case [24].

Table 6 Welding parameters
Full size table

5 Testing methodology

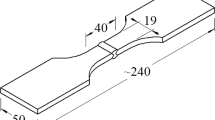
Test specimens with a long cylindrical middle section were used for the LCF tests on the base materials and the welded joints. In the case of the welded joints, the test specimens were manufactured in such a way that the weld lines are in the middle section of the test specimen. The shape and the dimensions of the test specimens are illustrated in Fig. 3.

Fig. 3
figure 3

Test specimen with long cylindrical middle segment

Full size image

During the LCF experiments, R =  − 1 stress ratio was used, with triangular loading wave form and with total strain amplitude control, at room temperature, in laboratory air, using MTS 312 universal electro-hydraulic materials testing equipment. An axial Le = 10 mm size strain gauge was used for the strain control. The loading frequency was 0.1 Hz. For the failure criterion, a 35% reduction of the maximal tensile force was set. MTS 680.12 type hydraulic grips were used for fixing the specimens during the tests. To compare the behavior of the base materials with the different strengths of the welded joints, test specimens were examined both from the base materials and the welded joints. The representative hysteresis loops were registered continuously during the tests and were used to determine the necessary attributes and relationships (Fig. 4).

Fig. 4
figure 4

Location of LCF test specimens in the welded joints

Full size image

From these data, we calculated the relation between the cycles to failure (Nt) and the total (εa), the elastic (εae), and the plastic (εap) strain amplitudes, which can be described with the following, widely accepted equation:

$${\varepsilon }_{a}={\varepsilon }_{ae}+{\varepsilon }_{ap}=\frac{{\sigma }_{f}^{^{\prime}}}{E}\bullet {N}_{t}^{b}+{\varepsilon }_{f}^{^{\prime}}\bullet {N}_{t}^{c}$$
(1)

In Eq. (1), σf', εf', b, and c are characteristic values, which can be determined from the test results. The plastic strain amplitude, which can be expressed with the Manson-Coffin empirical equation, is used only with a notch-free, cylindrical test specimen and with constant amplitude and frequency loading; there are many influences that can affect the results. Additionally, the elastic strain amplitude value, which is relatively small and difficult to determine from the hysteresis loops, was calculated from the stress amplitude; furthermore, the plastic strain amplitude was determined from the difference of the total strain and the elastic strain amplitudes [25, 26].

The plastic strain amplitude–stress amplitude relationship (so-called cyclic yield curves) was also drawn from the experimental results. We fitted a regression function to the experimental data in the form of a power function, approached to the data lines with the following equation:

$${\sigma }_{a50}=K\bullet {\varepsilon }_{ap}^{n}$$
(2)

In Eq. (2), σa50 is the stress amplitude belonging to 50% of the cycles to failure, while the parameters K and n were calculated from the experimental results [6].

6 Results and discussion

The LCF experiments were first performed on the S690QL steel category, on the base material, then on the welded joints, with matched and overmatched filler material. From the LCF experiments, the strain amplitude–cycles to failure diagram, presented in Fig. 5, could be determined for the S690QL base material and its differently matched welded joints. In this figure, the parameters of the equations for the elastic strain–cycles to failure and plastic strain–cycles to failure were also given with the square of the correlation indexes (R2 expresses the goodness of fit).

Fig. 5
figure 5

Strain amplitude–cycles to failure results of LCF tests performed on the S690QL steel grade and its welded joints

Full size image

After that, the specimens from the S960QL steel category were tested, again on the base material, then on the welded joints, with matched and undermatched filler material. The results can be seen in Fig. 6 along with the equations of the regression curves and the squared correlation indexes.

Fig. 6
figure 6

Strain amplitude–cycles to failure results of LCF tests performed on the S960QL steel grade and its welded joints

Full size image

Based on the figures and the relatively high correlation indexes, it can be concluded that all functions adequately fit to the measured data.

The welded joints have lower resistance to LCF compared to the base material. According to Fig. 5, the cycles to failure lag behind the base material at the same total and plastic strain amplitudes in the case of the welded joints. This is a consequence of the dendritic weld microstructure and the HAZ metallurgical changes. The curves of the total and plastic strain amplitudes of the matching joint are above the measured data on the overmatching joint. Therefore, the resistance to LCF of the matched welded joint is higher compared to the overmatching filler material. Regarding the elastic strain amplitudes of the S690QL base material and its welded joints at the same cycles, no significant difference was observed for the deviation of the results.

For the S960QL base material and its matched welded joint, the same statements are valid, namely the welded joint goes to failure at smaller cycles at the same total and plastic strain amplitudes. However, different behaviors were observed when the undermatching filler material was used. In the range of the higher strain amplitudes, the cycles to failure of the undermatched welded joints are higher at the same total and plastic strain amplitudes, while at smaller strain values, this relation is opposite; the cycles to failure are lower than for the matched welded joints. At the same cycles, the elastic strain amplitudes are nearly the same at the base material and the matched welded joint, while these values are lower at the undermatched welded joints.

In Fig. 7, the plastic strain–cycle to failure relations used by the designers are illustrated with the Manson-Coffin equations in a common diagram. The curves of the plastic strain amplitudes of the lower strength (S690QL) base material and its matched welded joint are above the same values of the higher strength steel (S960QL). There is no significant difference between the slopes of the curves. The plastic strain amplitudes belonging to the same cycles of the S960QL base material and its matching welded joint are in the same range as the overmatched welded joint of S690QL. The slope of this line slightly differs from the previously analyzed four curves. However, the slope of the plastic strain–cycles to failure curve of the undermatched joint of S960QL significantly differs from the previous ones.

Fig. 7
figure 7

Plastic strain amplitude–cycles to failure results of the LCF tests on the S690QL and S960QL base materials and their welded joints

Full size image

Based on the illustrated results in Fig. 8, the plastic stress amplitude–strain amplitude curves of the S960QL steel grade and its welded joints are above the S690QL base material and its welded joints due to its higher yield strength. No significant difference can be observed between the stress amplitudes of the S690QL base material and its matched welded joint, while higher stress values were measured in the overmatching case. The undermatching joint of S960QL resulted in a substantially lower plastic strain amplitude–stress amplitude curve than for the matched joint and the base material. The stress values are slightly above the overmatched joint of S690QL. The parameters of the regression curves (which are the parameters of Eqs. (1) and (2)) were determined from the test results in all cases. These data are summarized in Table 7 and Table 8. For the sake of comparison, some data from the literature [27, 28] about LCF experiments on different steels also can be found in these tables.

Fig. 8
figure 8

Stress amplitude–strain amplitude relations of the LCF tests on the S690QL and S960QL base materials and their welded joints

Full size image
Table 7 Parameters of the strain amplitude–cycles to failure approximate curves
Full size table
Table 8 Parameters of the plastic stress amplitude–strain amplitude approximate curves
Full size table

In the case of the S690QL steel, the welded joints have lower resistance against LCF than the base material; moreover, the overmatched welded joint has lower cycles to failure than the matched joints. In the case of the stress amplitude–plastic strain amplitude diagrams, the curves of the welded joint are always under those of the base materials. In the case of the S960QL steel, the base material and the welded joints have approximately the same cycles to failure regarding the total plastic strain amplitudes, while the plastic and the elastic strain amplitudes show similar behavior to the S690QL steel. Furthermore, for the plastic stress amplitude–strain amplitude diagrams, the same conclusions can be made on the S690QL steel. The S690QL base material has the highest plastic strain amplitude, while the S690QL welded joints and the S960QL steel and welded joints behave similarly. According to the plastic strain amplitude–stress amplitude diagrams, there is a definite connection between the strength and the stress amplitude value.

The location of crack initiation in the fine-grained base materials is illustrated in Fig. 9. The cracks initiated in the middle of the specimens during the fatigue tests. Regarding the welded joints, the LCF tests resulted cracks depending on the strength category and mismatch level. During the LCF tests, the cracks initiated in the same region (weld, HAZ) for one mismatch case (e.g., undermatching). The location of crack initiation in the matched welded joints of S690QL steel is found in the HAZ, typically in the subcritical zone (Fig. 10), while in the case of overmatched welded joints, crack initiation can be located on the boundary between the HAZ and the base material or between the HAZ and the weld metal (Fig. 11).

Fig. 9
figure 9

Location of crack initiation in the base materials: S690QL (a, c), S960QL (b, d, e) (etching: 2% HNO3)

Full size image
Fig. 10
figure 10

Location of crack initiation in the matched S690QL welded joint (etching: 2% HNO3)

Full size image
Fig. 11
figure 11

Location of crack initiation in the overmatched S690QL welded joint (etching: 2% HNO3)

Full size image

Hardness tests (Fig. 14) were also performed to explore in more details the circumstances of crack initiation and to analyze the results for the maximally permitted 450 HV10 according to EN ISO 15614–1 [23] for Q + T steels. The indentations were made 2 mm below the surface. In the case of matched S690QL welded joints, the measured hardness values in the HAZ were between 240 and 330 HV10, as compared to the 280–290 HV10 base material hardness and 260–270 HV10 weld metal hardness. In overmatched joints, higher hardness values were measured, between 320 and 330 HV10.

In the matched welded joint of S960QL, the crack initiation was located at the edge of intercritical and subcritical HAZ (Fig. 12), while in the undermatched joint, crack initiation was identified in the weld metal (Fig. 13). In the case of the matched welded joint, the measured hardness in the HAZ was between 260 and 290 HV10 in this subzone, compared to hardness value of 350–360 HV10 for the base material and 340–360 HV10 for the weld metal. The difference in hardness variations can be explained by the tempering and therefore softening of the original martensitic microstructure in the intercritical and subcritical HAZ subzones. In the case of the undermatched joint, lower hardness values (240–260 HV10) were measured near the crack initiation in the weld metal (Fig. 14).

Fig. 12
figure 12

Location of crack initiation in the matched S960QL welded joint (etching: 2% HNO3)

Full size image
Fig. 13
figure 13

Location of crack initiation in the undermatched S960QL welded joint (etching: 2% HNO3)

Full size image
Fig. 14
figure 14

Hardness distribution in the macro cross-section of the welded joints (M: matching, UM: undermatching, OM: overmatching)

Full size image

7 Conclusion

Based on the performed experimental work, the following conclusions can be drawn.

  1. 1.

    From the comparison of the low-cycle fatigue (LCF) data of the base materials and the welded joints, we found that in the case of identical total and plastic strain amplitudes, the welded joint can tolerate a smaller number of cycles until failure than the base material, in both materials examined.

  2. 2.

    In the case of the S690QL steel, with identical total and plastic strain amplitudes, the welded joints (both matched and overmatched) can tolerate smaller number of cycles until failure, than the base material. The LCF resistance of the matched welded joints is higher than that of the overmatched filler material. The overmatched welded joint decreases the LCF resistance for S690QL steels.

  3. 3.

    Regarding the relation between the S960QL base material and its matched welded joints, in the case of same total and plastic strain amplitudes, the welded joint fails at lower cycles. In the higher strain amplitude range, the number of cycles to failure was higher at the same total and plastic strain amplitudes when undermatched filler material was used. In the case of the lower strain values, an opposite ratio can be observed than for the matching filler material.

  4. 4.

    The curves related to the plastic strain amplitude of the lower strength (S690QL) base material and its matched welded joint were systematically above the values of the higher yield strength S960QL. Due to the higher yield strength, the plastic stress amplitude–strain amplitude curves of S960QL base material and its welded joints were above the values for the S690QL base material and its welded joints.

  5. 5.

    Analyzing the measured results and the data in the literature, the cyclic yield curves of higher strength steels and welded joints continuously are above the curves of the smaller strength steels. No definite tendency can be established between the cycles to failure and the yield strength in the case of equal plastic strain amplitudes.

  6. 6.

    For S690QL steel, the locations of crack initiation in the matched welded joints can be found at the heat-affected zone, typically in the subcritical zone, while in the case of undermatched welded joints, crack initiation can be located on the boundary between the HAZ and the base material or between the HAZ and the weld metal.

  7. 7.

    For S960QL steel, crack initiation was located at the edge of intercritical and subcritical HAZ, while in the undermatched joint, the crack initiation was identified in the weld metal. With lower strength filler materials, the cracks could be initiated under lower cycle to failure number; on the other hand, because of the large plastic region around the crack tip, the cracks could be propagated in a slower rate than in the case of higher strength filler materials.