Local approaches for the fatigue strength assessment of brazed joints made of X5CrNi18-10 and Cu 110 considering brazed seam quality and failure behavior

Abstract

In the case of cyclically loaded brazed joints, especially in safety-relevant components like common rail systems for common rail direct fuel injection, it is necessary to reliably estimate the fatigue strength, considering the influence of different manufacturing processes, manufacturing parameters, and failure behavior. In this paper, induction-brazed, vacuum-brazed, and continuous furnace-brazed joints are used to develop a reliable approach to assess the fatigue life. Therefore, the specimens were characterized and tested under load control using constant amplitudes. It is found that the local brazing geometry in conjunction with the surface condition, which differs by different topography values and by the position and number of initial defects, have the most influence on the failure behavior and consequently on the fatigue strength. Irrespective of this, however, it is shown that the fatigue strength can be estimated sufficiently well even with a simplified finite element modeling that uses idealized fillet radii and by taking support effects into account.

1 Introduction

Today, brazing is the preferred method in the automotive industry for manufacturing components for direct fuel injection like common rail direct injection. Due to the large number of joints, this is a very cost-effective joining method. Various joining processes are used, such as brazing in a continuous furnace, vacuum brazing, or inductive brazing. The brazing process is in general defined for process temperature above 450 °C, although the base material is still in a solid state (ISO 857–2, [1]). During the joining process, the so-called brazing material is formed due to diffusion processes between the base material and the brazing alloy. This exhibits new mechanical properties [2] compared to the brazing alloy. As a result of the manufacturing process, fillet radii with varying surface topologies are formed on the brazed components. The manufacturing process and the parameters used have a significant influence on the mechanical properties of the brazing material, the surface condition, and the profile of the fillet radii. These properties have an influence on the failure behavior and fatigue strength. Crack-like defects of different characteristics, which can reach deep into the brazing and are located in highly stressed areas of the fillet radii, have a significant influence on the fatigue strength [3, 4]. In [5], round specimens and T-joints, made of X5CrNiMo17-12–2 and brazed with AuNi18, were introduced to investigate the influence on the fatigue strength of added defined defects. It was shown that the influence of the defects was much greater compared to the influence of the heat treatment. An investigation of the failure mechanisms of stress-controlled brazed fatigue specimens under H₂ atmosphere was performed in [6]. It was found that the fracture occurred in the interface of the brazing zone and the crack propagation was characterized by interfacial jumps accompanied by ductile deformation features. In addition, by varying the shielding gas in the manufacturing process in [7], it was possible to influence the local fillet formation, which had an influence on the fatigue strength. Results of mechanically machined-brazed specimens in butt-joint configuration are predominant, where the influence on brazing time and brazing temperature [8], the influence of a subsequent heat treatment [9, 10], the influence of defined introduced defects [11,12,13], or the influence of corrosive environments [14] on the fatigue strength were investigated. In contrast, [15, 16] show results of fatigue tests on brazed specimens, without mechanical processing, with reference to the macrogeometric shape of the fillet.

Time and costs can be saved by a reliable fatigue assessment, which can already be carried out in the initial design phases. Even today, industry still relies mainly on experimental data from fatigue tests and practical experience, which leads to high costs in the design process. Approaches to numerical fatigue assessment of brazed components are described in [17,18,19], with the focus on crack propagation analyses starting from defects. Such a fracture mechanics approach is not feasible in industry due to the time and cost required. For this reason, investigations were carried out in [3] on brazed specimens and specimen-like components. Thereby, an evaluation of specimens brazed in a continuous furnace was successfully carried out on the basis of the maximum stresses σ_max,vMises occurring in the fillet. It is shown that the results of the fatigue tests can already be summarized in a reference S–N curve (Wöhler curve) with a fair scatter of T_S = 1:1.52 and a slope of k = 6.3. The scatter lies at the end of the range that is typical for individually statistically evaluated S–N curves of welded joints [20].

In this work, results of brazed joints with varying local brazing geometries and brazing qualities [3, 4], which have been extended in this work, are used to develop a reliable approach for estimating the lifetime. The fatigue tests were performed with the same test setup and under identical conditions and used in [4]. In addition, the same statistical analysis was carried out. In doing so, the evaluation should be made possible with as little numerical effort as possible for an industrial application, independent of manufacturing processes, manufacturing parameters and failure behavior.

2 Basic information about the used brazed joints

In the published works [3, 4], the stainless austenitic steel X5CrNi18-10 was defined as the base material (Table 1). The surface of the base material was specified as 2B according to DIN EN 10,088–2 [21].

Table 1 Chemical composition X5CrNi18-10 (weight-%, according to DIN EN 10,088–1 [22])

A brazing paste consisting of the Cu base filler metal Cu 110 according to DIN EN ISO 17672:2017–01 [23] and an organic binder was selected in [3, 4]. The detailed definition of the filler metal can be found in Table 2

Table 2 Chemical composition of the Cu 110 filler metal (weight-%, according to DIN EN ISO 17672 [23])

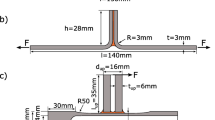
In [3], the study focused on the structural durability of brazed joints of rails for direct fuel injection. Based on analyses of the macroscopic dimensions and microstructure as well as the typical fracture properties of these brazed joints, shear and peel specimens were derived (Fig. 1). In addition, a more complex component-like specimen with a T-shape consisting of two tubes was developed based on the actual geometry of the application-relevant rails (Fig. 2). All geometric dimensions are documented in [3, 4].

Fig. 1

Geometries of peel and shear specimens for fatigue tests

Fig. 2

Component-like specimen with a T-shape for fatigue tests [3]

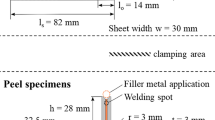
Figure 3 shows an additional small peel specimen type, which was additionally defined in this study for X-ray microscopic investigations. Due to the thinner base material, the crack propagation in the specimen can be observed non-destructively during fatigue tests.

Fig. 3

Small peel specimen type for X-ray microscopic investigations

3 Fatigue testing

In this study, the results from [4], which can be seen in Table 3, were extended by six test batches of vacuum-brazed shear and peel specimen each. The fatigue tests were performed with the same test setup and under identical conditions and used in [4]. The tests were tested to total fracture, i.e., number of cycles to failure N_f. For the shear specimens, total fracture is reached when the test cylinder displacement is increased by x ≥ 2 mm, resulting in complete separation of the sheets. In contrast, total fracture of the peel specimen is reached when the test cylinder displacement is increased by x ≥ 4 mm, and the specimens exhibit a cyclic stiffness decrease of k_cyc ≥ 60%. In this condition, the crack has propagated over the entire specimen width w deep into the joint area ≥ 8 mm.

Table 3 Fatigue test results from [4]

During the fatigue tests, photographs of the fillet radii r_H were taken at defined intervals. In addition, the cyclic stiffness of the specimens was recorded. For the failure criteria “number of cycles to crack N_crack” a crack length on the surface of a ≥ 1 mm is assumed as a technical crack and the same statistical analysis was carried out. N_crack is defined as the number of cycles until a crack length on the surface of a ≥ 1 mm could be measured based on the photographs and using the image scale. Due to the irregular crack-like surface of the radius of fillet r_H and several crack initiation areas, the assignment of an exact crack length on the surface is difficult. For this reason, the results should be treated with caution, as certain deviations are possible.

To investigate the failure behavior in more detail, a fatigue tests of the small peel specimen (Fig. 3) were performed at room temperature. The test was performed with a force-controlled servo-hydraulic testing machine with a constant load amplitude of F_a = 150 N, a load ratio of R_F = 0, and a test frequency of f = 30 Hz. An interruption of the fatigue test was performed after an interval of N = 50,000 cycles. The changes in the brazing material could be well visualized coupled computed tomography.

3.1 Results of peel specimen

The results of the extended fatigue tests, with the failure criterion: number of cycles to failure N_f, are shown in the statistical analysis (Fig. 4). With respect to the mean value, the highest number of cycles to failure N_f was achieved for the vacuum-brazed (Va) specimen with a brazing gap width of b = 100 μm (batch PG-6). These specimens also exhibit the lowest scatter. The crack initiation always began on the surface of the fillet radius r_H and the crack propagation subsequently proceeds along the joint area. Thus, all specimens show similar failure behavior.

Fig. 4

Statistical evaluation of fatigue strength tests with number of cycles to failure of peel specimens

Figure 5 shows the results of the extended fatigue tests in relation to the number of cycles to crack N_crack. In addition, the ratio between the number of cycles to crack and the number of cycles to failure N_crack/N_f is plotted. The vacuum-brazed specimens with a gap width of b = 50 μm show the largest and the specimens of batch PG-6 the smallest difference between the crack initiation and number of cycles to failure. Averaged over all peel specimens, the overall ratio is N_crack,total/N_f,total = 0.52. Except for vacuum-brazed specimens with a gap width of b = 200 μm and specimens of batch PG-4, an increase in the standard deviation of the specimen batches can be seen in each case.

Fig. 5

Statistical evaluation of fatigue strength tests with number of cycles to crack of peel specimens

3.2 Results of shear specimen

Figure 6 shows the statistical analysis of the extended fatigue tests, with the failure criterion: number of cycles to failure N_f, of shear specimens. In terms of the mean value, the highest number of cycles to failure N_f is achieved with the vacuum-brazed specimen from batch SG-7 with a gap width of b = 100 μm. In direct comparison with the peel specimens, the shear specimens of each batch show less scatter and the number of cycles to failure N_f determined in the different batches are closer to each other.

Fig. 6

Statistical evaluation of fatigue strength tests with number of cycles to failure of shear specimens

The highest number of cycles to crack initiation N_crack is achieved with the vacuum-brazed specimen of batch SG-6 and the induction brazed specimen (Fig. 7). In contrast, the vacuum-brazed specimen of the first batch (b = 50 μm and b = 200 μm) exhibit the lowest number of cycles to crack initiation N_crack. The continuous furnace-brazed specimen and the induction-brazed specimen show a similar fatigue strength. This indicates that the crack-like defects are in a less damaging form in the continuous furnace brazed specimen than in the vacuum brazed specimen of the first batch (b = 50 μm, b = 100 μm, and b = 200 μm). The vacuum-brazed specimens of the first batch (b = 50 μm and b = 200 μm) exhibit the largest and the induction-brazed specimens the smallest difference between the number of cycles to crack and the number of cycles to failure N_crack/N_f. Averaged over all shear specimens, the overall ratio is N_crack,total/N_f,total = 0.42.

Fig. 7

Statistical evaluation of fatigue strength tests with number of cycles to crack of shear specimens

Considering and averaging the results of both specimen types, the highest numbers of cycles to failure N_f and number of cycles to crack N_crack are achieved with vacuum brazed specimens of the PG- and SG-6 batches. A brazing temperature of T_braze = 1150 °C, a brazing time of t_braze = 2 min, and a cooling rate of ṫ = 60 K/min were used.

3.3 Failure behavior

3.3.1 Peel specimen

Figure 8 shows two-dimensional sectional images of the computed tomography (CT) reconstruction of a representative small peel specimen in the unloaded condition. In the CT reconstruction, the braze material is clearly distinguishable from the base material. Due to the higher atomic number of copper compared to iron, the brazing appears light gray in the CT image, while the base metal is shown in dark gray. Figure 8 shows the top view of a radius of the fillet r_H. It shows an open-pored structure with crack-like initial defects of different characteristics, which extend deep into the brazing material. The associated longitudinal section view in Fig. 8 illustrates the shape of the radius of the fillet r_H, showing the initial defects and their depth into the brazing material. This maximum depth in this initial defect is approx. 0.4 mm. The fillet topography is irregular and exhibits a clearly discernible roughness profile. The maximum depths of the crack-like initial defects are halfway between the interface area and the deepest point of the radius of the fillet r_H. These defects, which are for example visible and highlighted in the top view of a scanning electron microscope (SEM) image in Fig. 9, result from dendritic brazing solidification, which metallurgically leads to an open-pore cavity structure.

Fig. 8

Sectional images of the CT reconstruction of a representative and cyclically tested small peel specimen

Fig. 9

Top view of a fracture surface of a cyclically tested small peel specimen (SEM-image)

It is noticeable that immediately behind the fillet, crack-like initial defects and voids in the brazing are more pronounced than in the rest of the joining area, where only isolated defects were found. This crack-like surface condition of the fillet radius r_H has a considerable influence on the fatigue life and failure behavior under cyclic loading.

The changes in the brazing material after an interval of N = 50,000 cycles could be well-visualized with the aid of the small peel specimens coupled computed tomography. Figure 8 shows the location of crack initiation and further crack propagation. In the unloaded condition of the small peel specimen, crack-like initial defects of varying depth are evident on the radius of the fillet r_H. Point 1 in Fig. 8 indicates the initial defect in the unloaded condition, which led to crack initiation under cyclic loading.

A visible crack growth along the joining area began after about N = 550,000 cycles at the deepest initial defects of the fillet radii r_H (Fig. 8). After the crack initiation, the crack grows under further cyclic loading in the direction of the interface area, which is indicated by the direction of arrow 2, until the crack finally meets the base material (Point 3). The crack growth takes place along the shortest path from the site of crack initiation to the base metal (Fig. 8). After the crack met the base metal, further cyclic loading caused the brazing to peel away from the base material (Point 4). This peeling occurred up to the termination of the complete failure.

Figure 10 shows an etched small peel specimen. The different colors of the individual grains provide information about the grain orientation. Only a few grains exist over the height of the brazing gap width and that the crack growth occurs intergranular at different locations. In addition to the main crack, secondary cracks exist whose crack propagation always occurs in the direction of the boundary region between the brazing and the base material. A top view of a fracture surface also shows predominantly intergranular crack growth.

Fig. 10

Cyclically tested and etched small peel specimen

The study shows that the size, location, number, and depth of the initial defects of the fillet radii r_H can significantly affect the fatigue life.

3.3.2 Shear specimen

To further assess the failure behavior of shear specimens (Fig. 1), fatigue tests were stopped before complete specimen fracture and subsequently prepared metallographically and examined by SEM. The focus here was primarily on determining the crack initiation and crack propagation.

Possible starting points for cracks are voids, which are located in the volume of the radius of the fillet r_H below the surface (Fig. 11). Starting from the voids in the brazing material, several cracks run in the direction of the base material and the surface of the radius of the fillet r_H. Here, primarily intergranular crack growth can be observed. The right side of Fig. 11 shows the energy dispersive X-ray spectroscopy (EDS) analysis with an image resolution of 512 × 512 measurements. Cr- and Fe-rich intermetallic phases are distributed in the brazing material and form predominantly at the grain boundary. Ni and Si are uniformly distributed in the Cu matrix. In the case presented here, there is already considerable damage to the brazing material, which cannot be determined by a visual inspection of the surface of the radius of the fillet r_H.

Fig. 11

SEM image of crack propagation (starting from voids) in a radius of the fillet as well as the EDS analysis of the brazing material of a cyclically tested shear specimen

Figure 12 shows a section of a radius of the fillet r_H in the SEM. A vertical crack can be seen, which has its origin in an initial defect on the surface of the radius of the fillet r_H. In such a defect, local excess stresses occur under cyclic loading, leading to local material failure. The result is a crack, which grows under further cyclic loading. What can also be observed is that the crack grows along intermetallic phases, which form predominantly at the grain boundary (Fig. 12). Thus, the crack growth in the brazing material is intergranular. The intermetallic phases have a significantly higher hardness than the tough Cu matrix material. Correspondingly, high local stresses at these locations cannot be compensated by plastic micro-deformations.

Fig. 12

SEM image of crack propagation in a radius of the fillet of a cyclically tested shear specimen and a light microscope image of an etched region (Z) of the brazing gap

In the case of the shear specimens, two types of failure behavior occur during the fatigue tests. On the one hand, there is crack propagation along the interface between the base material and the brazing material and, on the other hand, crack propagation through the sheet metal base material in the area of the radius of the fillet r_H. These failure behaviors can also be observed in SEM images in Fig. 13 by corresponding crack propagation. In Fig. 13(a), the crack proceeds intergranular toward the base metal. At the interface between the brazing and the base metal, the crack changes direction along the interface. In Fig. 13(b), on the other hand, the crack runs into the base metal. The interface becomes more “toothed” with increasing erosion, which occurred more intensely in the induction brazed specimens, and thus provides greater resistance to crack propagation. This promotes crack propagation into the base metal.

Fig. 13

SEM images of corresponding crack propagation of cyclically tested shear specimen

Accordingly, it can be stated that local material properties in the interface region, such as the strong dissolution of the base material, and the size, position, and number of crack-like initial defects have an influence on the failure behavior. The type of crack propagation may depend not only on the local material properties and initial defects but also on the load ratio R_F. This influence has not been investigated in this work but should be considered in further investigations.

4 Finite element models

To determine the brazed joint stresses, parametric finite element (FE) models of the peel and shear specimens (Fig. 1) were set up. Input variables for the FE models of the peel and shear specimens are, in addition to the geometry of the semi-finished products such as bending radius R, sheet thickness t and sheet width w, also the sizes of fillet radii r_H, brazing gap width b and angular distortion α which occur after the joining process. Due to the rounding of the sheets in the shear specimens, these specimens were simulated as a 3D volume model (Abaqus 2020, C3D20-hexaeder elements). For the peel specimens, on the other hand, a simplified representation using 2D volume elements with a plane strain state (Abaqus 2020, CPE8-hexaeder elements) was used. In addition, detailed 3D volume models (Abaqus 2020, brazing: C3D10-tetraeder elements, sheets: C3D20-hexaeder elements) were built using high-resolution 3D scans and subsequent “reverse engineering” of one vacuum brazed peel and one shear specimen each, to achieve the most realistic representation possible of the fillet geometry within the FE model and thus to determine the most realistic stress distributions possible. In the models, both materials were modeled as different volumes with elements of a quadratic approach function and characteristic values adapted to the material were assigned to them. For the steel, a Young’s modulus of E = 210 GPa and a Poisson’s ratio of ν = 0.3 were applied, for the brazing material E = 122 GPa and ν = 0.35.

The brazing gap widths b of the specimens were adjusted and fixed by gas tungsten arc (GTA) spot-welding of both semi-finished products before brazing [4]. FE simulations were used to investigate the influence of the spot welds on the stiffness of the specimens and thus also on the local stresses of the brazing material. For this purpose, the spot welds were considered in one FE volume model each of shear and peel specimens. It was found that the weld spots have a negligible influence < 0.1% and therefore do not have to be considered.

4.1 Specimens with idealized fillet geometry (fine mesh)

In the case of the peel specimens, the radius of the fillet r_H was meshed with hexahedral elements in the relevant region and was mapped with multiple layers with an element thickness of E_t < 0.05 mm. Over the relevant range of fillet radius r_H, 16 elements were used in each case. In the case of a very small fillet radius of, for example, r_H = 0.26 mm, this results in element edge lengths of approx. E_l = 0.02 mm and a total element count of approx. n_tot = 3800. In contrast, a very large fillet radius of, for example, r_H = 2.76 mm results in element edge lengths of approx. E_l = 0.2 mm with a total element count of n_tot = 3400. The maximum element edge length in the model corresponds to E_l,max = 0.5 mm.

For the shear specimens, the radius of the fillet r_H was meshed in the relevant area using hexahedral elements and with at least two layers with an element thickness of E_t < 0.05 mm. Over the fillet radius r_H, 24 elements were used in each case. In the case of a very small fillet radius of, for example, r_H = 0.33 mm, this results in element edge lengths of approx. E_l = 0.02 mm and a total element count of approx. n_tot = 580,000. In contrast, a very large fillet radius of, for example, r_H = 2.45 mm results in element edge lengths of approx. E_l = 0.17 mm with a total element count of n_tot = 57,000. The maximum element edge length in the model corresponds to E_l,max = 1 mm.

The procedure for meshing was created based on [24]. Both, the strain comparison between experimentally determined and simulated strains of the peel and shear specimens shows high agreement.

The maximum local notch stress σ_max,vMises as well as the stress gradient χ at the most highly stressed point were determined for all specimens (Fig. 14). The minimum element thickness E_t of the respective FE model was used as the evaluation depth ∆x in each case. The stress gradient χ was determined as follows:

Fig. 14

Stress distribution in the most highly stressed area of the fillet radius according to v. Mises for the peel and shear specimen with idealized geometry

$$\upchi =\frac{1}{{\upsigma }_{\mathrm{max}}}\bullet \frac{\Delta\upsigma }{\Delta \mathrm{x}}=\frac{1}{{\upsigma }_{\mathrm{max}}}\bullet \frac{{\upsigma }_{\mathrm{max}}-{\upsigma }_{\mathrm{evaluation\;depth}}}{\Delta \mathrm{x}}$$

(1)

Due to the different geometry of the specimens, no uniform parameter such as “MPa notch stress per F = 1 kN” can be given for the specimens.

4.2 Specimens with realistic representation of fillet geometry

A 3D measurement system was used for the high-resolution 3D scans. Subsequently, the stl-data were converted into CAD-data with the help of reverse engineering software and checked by means of a surface comparison (Fig. 15), which shows a high level of agreement.

Fig. 15

High-resolution 3D scans and “reverse engineering” of the geometry’s of peel and shear specimens

Due to the complex contour of the CAD-data, the sheets and the brazing material were created as separate parts, meshed and then joined by “tie contact.” The brazing material was meshed with tetrahedral elements (Abaqus 2020, C3D10-tetraeder elements) and the steel sheets with hexahedral elements (Abaqus 2020, C3D20-hexaeder elements). In the models, both materials were modeled as different volumes with elements of quadratic shape function and assigned characteristic values adapted to the materials.

In both models, the brazing was meshed in the relevant area of the fillet radius r_H with elements of element edge length E_l = 0.02 mm. The sheets were meshed in the joining area with an element edge length of E_l = 0.1 mm and outside with a maximum element edge length of E_l,max = 1 mm. In the case of the peel specimen, the total number of elements was approx. n_tot = 335,000 and in the case of the shear specimen approx. n_tot = 1,300,000.

In the case of the surface topology of the fillet radii r_H from the 3D scans, there are inhomogeneous stress distributions with local stress increases in contrast to the idealized fillet radii r_H (Fig. 16 and Fig. 17). In the case of the peel specimens, there are higher local stresses by a factor of approx. 2.2 in the 3D scan model compared to the model with idealized geometry. In contrast, this factor is approx. 1.5 for the shear specimen. Depending on the number and location, these local stress peaks can lead to early crack initiation and thus have a significant negative influence on the fatigue strength. In reality, significantly higher excess stresses can occur, since the initial defects, which can be seen in Fig. 8, are not correctly represented in the simulation in terms of their complexity and their depth into the brazing material. These local stress peaks can lead to early crack initiation and thus have a significant negative influence on the fatigue strength.

Fig. 16

Stress distributions of the 3D scan of the peel specimen compared with the model with idealized geometry

Fig. 17

Stress distributions of the 3D scan of the shear specimen compared with the model with idealized geometry

As for idealized specimens, the gradient $\chi$ was also evaluated for 3D-scanned specimens. For the 3D-scanned shear specimen, the gradient is $\chi$ = 19.4 and for the idealized one $\chi$ = 3.6 results in a less factor of 5.4. In the case of the 3D-scanned peel specimen, the gradient is $\chi$ = 18.9 and for the idealized $\chi$ = 3.1 results in a less factor of 6.1.

4.3 Simplification of FE modeling for industrial application

For an industrial application, a fatigue strength assessment with the lowest possible numerical effort is desirable to save time as well as costs in the design process. For this purpose, the correlation between the stress gradient χ and the fillet radius r_H for the peel and shear specimens was determined with the aid of the FE models with idealized geometry (Fig. 18).

Fig. 18

Correlation between the stress gradient and the fillet radius

In the case of shear specimens, the correlation in the range of 0.3 mm ≤ r_H ≤ 3 mm can be described as follows:

$$\chi \text{=3.052}\bullet {{\text{r}}_{\text{H}}}^{-0.867}$$

(2)

For the peel specimens, the relationship in the range of 0.3 mm ≤ r_H ≤ 3 mm is as follows:

$$\chi \text{ = 2.183}\bullet {{\text{r}}_{\text{H}}}^{-0.974}$$

(3)

With the trend line derived from the results mapping the averaging between shear and peel stress, the correlation in the range of 0.3 mm ≤ r_H ≤ 3 mm can be described as follows:

$$\chi \, \text{=} \, \text{2.581}\bullet {{\text{r}}_{\text{H}}}^{-0.921}$$

(4)

Through the determined $\chi$-${\mathrm{r}}_{\mathrm{H}}$ relationship from shear and peel specimens, only the maximum local notch stress of the fillet radii r_H must be determined, whereby a sufficient simulation convergence of ≤ 5% should be achieved. Subsequently, the effective stress σ_eff, see Section 5.2, can be calculated, which allows a fatigue assessment with consideration of the support effect.

For the demonstration of the evaluation, FE models were built with a significantly reduced number of elements for the peel and shear specimens (Fig. 19). In the case of the peel specimens, six hexahedral elements with an element thickness of E_t = 0.05 mm were used in the first layer over the relevant area of the fillet radius r_H. This resulted in a maximum total element number of n_tot = 341. In the case of the shear specimens, the relevant area of the fillet radius r_H was meshed with four hexahedral elements with an element thickness of E_t = 0.05 mm in the first layer, resulting in a maximum total element count of n_tot = 6993.

Fig. 19

FE models (peel and shear specimens) with a low number of elements for an industrial application

With the simplified modeling presented here, a percentage deviation of the maximum local notch stresses of the fillet radii r_H averaged over all specimens of 2% and a maximum deviation of 5% was achieved compared to the modeling from Section 4.1. Accordingly, these can be recommended for industrial application.

5 Fatigue strength assessments

5.1 Based on maximum notch stresses

In [3], an evaluation of specimens brazed in a continuous furnace was successfully carried out on the basis of the maximum stress amplitudes σ_a,max,vMises determined in radius of the fillet radius r_H. It is shown that the results can already be summarized in a reference S–N curve. This S–N curve has a scatter of T_S = 1:1.52 and a slope of k = 6.3. The scatter lies at the end of the range that is typical for individually statistically evaluated S–N curves of welded joints [20].

Since the database (local stresses σ and stress gradients χ) from [3] was established using von Mises stresses σ_vMises and satisfactory results were obtained, the analysis of the experimental data from [4] and the extended data in this paper is also based on von Mises stresses σ_vMises. As described in [25], there is a correlation between the von Mises stress σ_vMises and the first principal stress σ₁ on the surface of a notch when there are no shear stresses (τ_xy = 0) on the surface. For a Poisson’s ratio of v = 0.3, the relationship is as follows:

$${\upsigma }_{\mathrm{v}\mathrm{Mises},\mathrm{v}=0.3}=0.89\bullet {\upsigma }_{1}$$

(5)

For the Poisson’s ratio of v = 0.35 used for brazing, the correlation for the shear and peel specimens evaluated here is given as follows:

$${\upsigma }_{\mathrm{v}\mathrm{Mises},\mathrm{v}=0.35}=0.88\bullet {\upsigma }_{1}$$

(6)

This results in 12% higher values for the first principal stress σ₁. Accordingly, the generation of the reference S–N curve should also be possible with reference to the first principal stress σ₁, which, however, was not further investigated within the scope of this work.

Figure 20 shows the reference S–N curve with the 10%, 50%, and 90% survival probability and experimental results from [3]. In addition, the test results from [4] with the maximum v. Mises stresses σ_a,max,vMises of the fillet radii r_H plotted against the determined number of cycles to failure N_f of the fatigue tests and the extended fatigue tests of this study are shown. A significant proportion of the specimens from [4] and the extended fatigue tests of this study lie well outside the scatter of T_S = 1:1.52. It is striking that in this context specimens with small fillet radii r_H tend to lie in the conservative range, i.e., the fatigue life is underestimated according to [3], and peel specimens with very large fillet radii r_H ˃ 1.2 mm lie in the non-conservative range, i.e., the fatigue life is overestimated according to [3]. The overassessment of the fatigue life of peel specimens with very large fillet radii r_H ˃ 1.2 mm can be explained by the crack-like initial defects on the surface of the fillet radii r_H with resulting inhomogeneous stress distributions and voids in the brazing volume, which have a negative influence on the fatigue strength under peeling stress.

Fig. 20

Reference S–N curve and test results from [3] compared with test results from [4] and the extended fatigue tests of this study

In addition, an influence on the fatigue strength can be seen due to the different failure behavior of the shear specimens. Compared to the induction brazed specimens, the vacuum-brazed shear specimens exhibit significantly earlier crack initiation with respect to fatigue life and crack propagation along the interface between the base material and the brazing material, [4]. This failure behavior can lead to significantly later or, in extreme cases, no crack initiation by the base material, which has a major impact on the sum of cycles to failure N_f. For this reason, with reference to comparable maximum stresses σ_a,max,vMises, the vacuum-brazed specimens tend to achieve higher cycles to failure N_f compared with the induction brazed specimens. This becomes particularly clear when considering the vacuum-brazed specimens, which exhibit joining failure exclusively at the interface between the base metal and the brazing material, without complete fracture through the base metal.

The statistical evaluation of the results from [3] as well as the results from [4] and the extended fatigue tests of this study, each evaluated without run outs, results in a reference S–N curve with a large scatter of T_S = 1:3.1 and a steep slope of k = 2.2 (Fig. 21). The slope is thus outside the typical range of k = 3–8 for welded components made of steel, aluminum, and magnesium alloys with a sheet thickness of t ≤ 7 mm [26, 27]. For a reliable fatigue assessment, the reference S–N curve used should have a scatter T_S as small as possible to not lose any lightweight potential by designing the brazed components. For this reason, the fatigue strength assessment based on the maximum notch stresses and considering different manufacturing processes, manufacturing parameters, and failure behavior of brazed joints is not target-oriented and therefore not recommended.

Fig. 21

Statistical evaluation (resulting reference S–N curve) of the results from [3] as well as the results from [4] and the extended fatigue tests of this study, each evaluated without run outs

5.2 Taking into account the support effect

A fatigue strength assessment, e.g., according to the FKM guideline [28], is not possible because no information is available on its support effect in general for copper materials and specifically for the brazing material. However, this supporting effect is a relevant influencing variable for the fatigue strength evaluation and leads to an increase of the endurable local notch stresses σ_a,max,vMises depending on the existing stress gradient χ. With the help of the stress gradient χ and the characteristic fatigue value S_g, the so-called support factor $n$ can be calculated:

$$n \text{= 1 + }\sqrt{{\text{s}}_{\text{g}}\chi }$$

(7)

The support factor $n$ can then be used to calculate the effective stress σ_eff according to [29, 30]:

$${\upsigma }_{\mathrm{eff}}=\frac{1}{\mathrm{n}}\bullet {\upsigma }_{\mathrm{max}}$$

(8)

The parameter S_g can be interpreted as a characteristic fatigue value for the brazing material. Since S_g is not known, it had to be determined empirically by variation. According to [29], a technically relevant range of the characteristic fatigue parameter S_g of 0.001 mm ≤ S_g ≤ 0.150 mm is given. In [3], the minimum of the scatter T_S was determined at S_g = 0.02 mm for peel and shear specimens and demonstrator components brazed in a continuous furnace. When establishing the reference S–N curve with consideration of the support effect using the results from [3] as well as the results from [4] and the extended fatigue tests of this study, each evaluated without run outs, the minimum of the scatter T_S could only be determined empirically for a value of S_g = 2 mm (Fig. 22). Beyond this value, no further significant improvement can be achieved. For this reason, the characteristic fatigue value was set at S_g = 2 mm. It must be noted that the characteristic fatigue value S_g is clearly outside the specified technically relevant range from [29].

Fig. 22

Scatter of the reference S–N curve (with consideration of the support effect) for different characteristic fatigue values

The characteristic fatigue value S_g determined here is not a pure material characteristic value and does not apply generally to the brazing used. Rather, it is coupled with the idealized modeling. The value is therefore also influenced by the fact that the actual stress concentration is much higher than that calculated by FE based on the idealized geometry. This could be an explanation for the high value of S_g = 2 mm.

Considering the support effect, using a characteristic fatigue value of S_g = 2 mm, a reference S–N curve is obtained, see Fig. 23, with a slope of k = 3.4 and a scatter of T_S = 1:1.8. This scatter is slightly above the range which is typical for individually statistically evaluated S–N curves of welded joints [20]. In [31], scatters of reference S–N curves of welded joints can be found, resulting in a range of T_S = 1:1.70–1:2.03. Thus, the scatter of the reference S–N curve with consideration of the support effect is in a typical range for welded joints. Despite the consideration of different manufacturing processes, manufacturing parameters and failure behavior, the fatigue assessment for brazed joints is evaluated as good and purposeful.

Fig. 23

Reference S–N curve (with consideration of the supporting effect) with statistical evaluation of the test results from [3] and [4] and the extended fatigue tests of this study

An influence by the different failure behavior of the shear specimens can also be seen in the fatigue strength evaluation considering the support effect. The vacuum brazed specimens, with reference to comparable effective stresses σ_eff, exhibit higher cycles to failure N_f compared with the induction brazed specimens. This is particularly true for the vacuum-brazed specimens, which exhibit joining failure exclusively at the interface between the base material and the brazing material, without complete fracture through the base material.

However, specimens that lie in the non-conservative range even after taking the support effect into account show that the fatigue life of the specimens is not determined by the size of the fillet radius r_H alone, but that brazing quality and failure behavior must also be considered. Overassessment of fatigue life can be explained by voids in the brazing volume and the size, location and number of crack-like initial defects on the surface of the fillet radii r_H, which can extend deep into the brazing and are located in highly stressed areas of the fillet radii r_H. These have a considerable influence on the fatigue strength, especially in the case of large fillet radii r_H under peeling stress. For this reason, components with large fillet radii r_H due to manufacturing should be subjected to a sufficient safety factor, especially if crack-like initial defects are present on the fillet radii r_H and predominantly peeling stresses are to be expected.

With the fatigue value of S_g = 2 mm, this results in an effective stress of σ_eff,a = 49.4 MPa for the 3D-scanned shear specimen and σ_eff,a = 62.8 MPa in the case of the idealized shear specimen, giving a percentage difference of 21.4%. For the 3D scanned peel specimen, this results in an effective stress of σ_eff,a = 60.6 MPa and σ_eff,a = 55.8 MPa for the idealized peel specimen, giving a percent difference of 8%. Despite the differences, the points fall within the scatter band T_S of the reference S–N curve and can thus be evaluated sufficiently well with both model variants (Fig. 23).

For a fatigue assessment, a tolerable effective stress amplitude of σ_eff,a = 13.2 MPa at N = 1·10⁷ cycles and a slope of k = 3.4 should be assumed. These values are backed by a survival probability of P_S = 97.5%. No information on a knee point could be determined.

5.2.1 Cycles to failure vs. cycles to first crack

In the case of linear-elastic stresses, only the number cycles to crack N_crack can be used in principle for a fatigue assessment, since crack initiation with subsequent crack propagation can only be correctly mapped by means of elastic–plastic or linear-elastic fracture mechanics. However, since the acquisition of the cycles of number to crack N_crack is comparatively time-consuming, the number of cycles to total failure N_f is usually used in the literature for a fatigue strength assessment. Thus, this approach always includes a certain amount of crack propagation, which can have an influence on the quality of the evaluation in the case of strongly varying failure behavior. For this reason, an evaluation was also carried out based on the number of cycles to crack N_crack of induction and vacuum brazed as well as continuous furnace brazed peel and shear specimens determined in this research project.

The statistical evaluation with a characteristic fatigue value of S_g = 2 mm results in a reference S–N curve with a slope of k = 2.3 and a scatter of T_S = 1:1.92 with reference to the number of cycles to failure N_f. In contrast, a reference S–N curve with a shallower slope of k = 3.3 and a lower scatter of T_S = 1:1.68 results when using the number of cycles to crack N_crack (Fig. 24).

Fig. 24

Yieldable effective stresses with S_g = 2 mm of induction, vacuum, and continuous furnace-brazed peel and shear specimens plotted against the number of cycles to failure N_f and number of cycles to crack N_crack

With reference to the reference S–N curve with the failure criterion “number of cycles to crack initiation,” the induction-brazed shear specimens achieve higher number of cycles to crack N_crack at comparable effective stresses σ_eff compared to the vacuum-brazed shear specimens, due to the more homogeneous fillet radii r_H without crack-like initial defects [4]. This can be explained by more homogeneous local stress distributions, which lead to a longer crack initiation phase.

5.3 Industrial assessment

In direct comparison with the reference S–N curve, the test points are predominantly within the scatter band of T_S = 1:1.8 (Fig. 25). However, due to the respective deviation of the averaged trend line from the actual results (Fig. 18), some points are slightly outside the scatter T_S = 1:1.8. In this case, the peel specimens, especially in the case of low effective stresses σ_eff, tend to lie in the range of the 90% survival probability curve. In contrast, shear specimens tend to be predominantly in the range of the 10% survival probability curve. Accordingly, components with large fillet radii r_H that experience predominantly peeling stresses should be subjected to a sufficient safety factor, especially if crack-like initial defects are present on the fillet radii r_H.

Fig. 25

Comparison of the industrial evaluation with created reference S–N curve with consideration of the support effect

6 Discussion

The size, position, and number of crack-like initial defects, which protrude deep into the fillet radius volume, have a considerable influence on the fatigue life and failure behavior under cyclic loading, especially when peel loading is present. Accordingly, brazed components with large fillet radii r_H due to manufacturing, which experience predominantly peel loading, should be subjected to an adequate safety factor. This applies if crack-like initial defects are present in a pronounced form on the fillet radii r_H. In addition, peel loading can be reduced by design measures to further minimize the percentage possibility of overestimating the fatigue life.

By evaluating the fatigue strength based on the maximum occurring notch stresses with the reference S–N curve from [3], the fatigue life of specimens with small radii of the fillet r_H is underestimated and the fatigue life of peel specimens with very large radii of the fillet r_H ˃ 1.2 mm is overestimated. In the statistical evaluation of the results from [3] as well as the results from [4] and the extended fatigue tests of this study, each evaluated without run outs, based on the maximum notch stresses that occur, a reference S–N curve results with a very large scatter of T_S = 1:3.1. However, for a reliable fatigue strength evaluation, the reference S–N curve used should have as small a scatter T_S as possible in order not to lose any lightweight potential by designing the components too conservatively. For this reason, the fatigue strength assessment based on the maximum notch stresses and considering different manufacturing processes and manufacturing parameters of brazed joints is not target-oriented and therefore not recommended.

A significant influence of the support effect was determined, resulting in a characteristic fatigue value for the brazing material of S_g = 2 mm. The parameter cannot be regarded as a pure material parameter for the brazing material used, since it is also coupled to the idealized modeling. It is suspected that the high value of S_g = 2 mm is influenced by the fact that the actual stress concentration is significantly higher than calculated. In addition, it is an indication of a high support effect of the brazing material. However, no clear separation between the influences could be identified in the course of this work.

Due to the determined correlation between the stress gradient χ and the fillet radius r_H with a range of validity of 0.3 mm ≤ r_H ≤ 3 mm, only the maximum local notch stress of the fillet radii r_H must be determined, whereby a sufficient convergence of ≤ 5% deviation of the simulation results should be achieved. Then, the effective stress σ_eff can be calculated and the fatigue assessment can be performed using the reference S–N curve with consideration of the support effect. Due to the typical scatter T_S of the reference S–N curve with consideration of the support effect for welded joints, the developed method for fatigue strength assessment for the brazed joints investigated here, limited to the used materials, manufacturing processes/parameters, test conditions, and the occurring failure behavior, is evaluated as acceptable and target-oriented.

7 Conclusions and outlook

The main conclusions can be drawn from the presented investigations:

• Crack-like initial defects have a considerable influence on the fatigue life and failure behavior under cyclic loading.

• It is advisable to carry out the modeling as realistically as possible with idealized brazing radii and to separate the materials between brazing material and base material. The values for copper can be used as modulus of elasticity and transverse contraction coefficient.

• By evaluating the fatigue strength based on the maximum occurring notch stresses according to [3], the fatigue life of specimens with small radii of the fillet r_H is underestimated and the fatigue life of peel specimens with large radii of the fillet r_H is overestimated. For this reason, the fatigue strength assessment based on the maximum notch stresses and considering different manufacturing processes, manufacturing parameters, and failure behavior of brazed joints is not target-oriented and therefore not recommended.

• In terms of the fatigue life, a significant influence of the support effect was determined. Due to the typical scatter T_S of the reference S–N curve with consideration of the support effect for welded joints, the fatigue strength assessment for brazed joints investigated here, limited to the used materials, manufacturing processes/parameters, test conditions and the occurring failure behavior, is evaluated as acceptable and target-oriented.

• For a fatigue assessment, a tolerable effective stress amplitude of σ_eff,a = 13.2 MPa at N = 1·10⁷ cycles and a slope of k = 3.4 should be assumed. These values are backed by a survival probability of P_S = 97.5%. No information on a knee point could be determined.

For an application in industry, further investigations should be carried out to be able to consider influences of harmful environmental influences such as corrosive media or high operating temperatures in the fatigue strength evaluation. In addition, further fatigue tests should be carried out to identify influences on the fatigue strengths such as varying frequencies, variable amplitudes, variation in brazing application, or particle addition in the brazing paste. The transferability of the fatigue strength assessment with consideration of the support effect to other material combinations and validation on brazed components should also be examined.