1 Introduction

The pursuit for an energy-, material-, and resource-efficient manufacturing of components and structures in the aerospace industry requires high-tech manufacturing methods and processes [1]. One future-oriented manufacturing method in this context is additive manufacturing and especially for large structural parts, wire arc additive manufacturing [2, 3]. Additive manufacturing offers several advantages compared to conventional processes, especially when high cost materials, such as the titanium alloy Ti-6Al-4 V which is widely used in the aerospace industry, are processed [4]. In the WAAM process, a solid wire is fed as a base material, melted by means of an electric arc as an energy source, and deposited layer by layer [5]. High deposition rates are required for an efficient production, whereby high energy or heat input is necessary. Due to large temperature gradients, the formation of complex distortion and residual stress states may occur, which can significantly influence the process reliability and product tolerances [6,7,8].

To improve the process reliability and therefore enhance the quality of WAAM components, it is necessary to minimise distortion and residual stress. Hence, extensive parameter studies are crucial to optimise the WAAM process regarding the minimization of these conditions. As experimental studies are time- and cost-consuming, the need for numerical tools to substitute these experimental studies is obvious [9, 10]. Hence, various numerical approaches exist for the estimation of residual stresses and deformations during and after additive manufacturing processes. Thermomechanical finite element simulation is one commonly used tool for process optimization and provides the opportunity to investigate relevant factors influencing distortion and residual stress state [11, 12].

Current studies on the validation and calibration of thermomechanical process simulation with experimental data from additive manufacturing processes reveal an overestimation by the simulation results regarding residual stress and distortion [13, 14]. This overestimation in the simulation may be due to a major simplification of the material characteristics by not taking into account viscoplastic material behaviour, such as creep or stress relaxation [15, 16]. However, the characteristic layer-by-layer additive manufacturing can lead to viscoplastic effects in the structure and should be therefore considered in the simulation, especially because Ti-6Al-4 V is quite sensitive with respect to viscoplastic effects [17]. In [18,19,20], viscoplastic effects are captured in the thermomechanical simulation of the WAAM process by the implementation of stress relaxation. Additionally, a Norton Bailey creep model [21, 22] is explicitly implemented in the WAAM simulation in [23]. In contrast to the simulation methods considering stress relaxation or creep, no material model is found in the literature implementing a Chaboche model in the thermomechanical WAAM simulation.

Therefore, this study aims to investigate the influence of temperature, strain amplitude, and strain rate on the elasto-viscoplastic material behaviour of wire arc additively manufactured Ti-6Al-4 V. A Chaboche material model is implemented in the thermomechanical simulation of the WAAM process for a detailed description of the elasto-viscoplastic behaviour and a more accurate estimation of the residual stress and distortion state in the WAAM part. Moreover, the implemented material model is validated by comparison of residual stress state and distortion with measured data of a ten-layer WAAM part.

2 Experimental method

2.1 Materials and additive manufacturing

The elasto-viscoplastic material behaviour of Ti-6Al-4 V was investigated in this study. The titanium alloy Ti-6Al-4 V was used for both the substrate and wire. The nominal chemical composition according to the manufacturer’s specifications of the substrate and the wire is shown in Table 1. For the additive manufacturing of the structures, a 1.6-mm-diameter wire consumable was additively added layer-by-layer on a substrate. WAAM structures were manufactured with a plasma arc welding machine combined with a 4-axis gantry robot and a double wire feeder to establish higher deposition rates. A deposition rate of about 3.3 kg/h was maintained with an energy per length of about 106 J/m, an average power of 6 kW, and a travel speed of about 5 mm/s, which is comparable to data from literature [24]. To protect the weld pool as well as the heat-affected zone from oxidation and undesirable contamination, the process was carried out in a pure argon (99,9999%) filled fixed box chamber with an overall size of about 3 × 3 × 4 m3. The purity of the atmosphere was maintained by purging with fresh argon and continuously cleaning the atmosphere by a recirculation device.

Table 1 Chemical composition of the used material in weight %, comparable to [25, 26]
Full size table

In total, two WAAM structures were built, one structure for specimen extraction and development of the material model and the other one for validation of the enhanced thermomechanical simulation. Both WAAM walls were manufactured with the same parameter set, utilising a single-layer building strategy with the same direction of deposition in each layer. Dwell times during the process were set to ensure a constant interpass temperature of around 400 °C, comparable to the literature [27]. The structure for the extraction of the specimens consisted of 40 layers with a total length of about 400 mm and was built on a substrate with the dimensions of 500 × 100 × 13 mm3, see Fig. 1a. In comparison, the structure for validation consisted of ten layers with a length of about 120 mm and was deposited on a 200 × 50 × 13 mm3 substrate, shown in Fig. 1b. The effective wall thickness of both WAAM walls was measured to be about 14 mm, and the average layer height was evaluated to be about 3.3 mm for the high structure and 3.5 mm for the validation structure.

Fig. 1
figure 1

WAAM structures for specimen extraction (a) and for model validation (b)

Full size image

2.2 Test procedure

Quasi-static tensile, low cycle fatigue, and complex low cycle fatigue tests were conducted to investigate the elasto-viscoplastic material’s behaviour. As the materials’ behaviour strongly depends on the manufacturing and fabrication history, the material behaviour of the additively manufactured structure as well as of the substrate was investigated. Therefore, on the one hand, specimens were extracted from an additional, unprocessed titanium base plate used for the WAAM substrate, and on the other hand, specimens were fabricated out of the WAAM structure itself. An unprocessed plate with dimensions of 300 mm in width, 250 mm in length, and 13 mm thickness was used for the extraction of the specimen for material characterisation of the substrate material. The manufactured WAAM structure was cut into three parts, and from each of these, specimens were cut out horizontally, parallel to the deposition direction, see Fig. 2b. To ensure a similar microstructure and to avoid any influence of the extraction position, specimens were extracted above the sixth deposited layer, where a constant heat balance during the process was assumed. Additionally, about a 40 mm distance at the start and at the end of the wall was cut off to avoid any starting or ending effects.

Fig. 2
figure 2

Geometry of tested specimen in [mm] (a) and scheme of the location of the test specimen (b)

Full size image

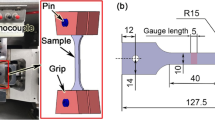
Cylindrical test specimens with a total length of 120 mm and a clamping diameter of 12 mm were used for the tests. The test area in the centre of the specimens was defined with a diameter of 7 mm and an initial test length of 20 mm. The dimensions of the specimen geometry are shown in Fig. 2a. Basically, the specimen geometric dimensions were defined to obtain samples out of the structure and for a homogenous temperature field in the test area. The surface of all specimens was polished after machining of the final contour to avoid surface roughness effects.

For experimental tests, an uniaxial, servo-hydraulic test cylinder with a nominal load capacity of 100 kN was used. To measure the strain during room temperature (RT) tests, a contacting Instron extensometer with an initial length of 12.5 mm and a maximum deflection of ± 5 mm was applied. In comparison, strain measurement during the high temperature (HT) tests was conducted by means of a contacting ceramic extensometer with an initial length of 12.6 mm and a measuring range of ± 1.8 mm, shown in Fig. 3. Specimens were clamped on both ends using water-cooled hydraulic grips and clamping sleeves. All tests were performed in strain-controlled test mode. To perform high-temperature tests, test specimens were heated by optimised induction coils and an induction heating system using a 10 kW medium frequency generator. Within the initial test length, the temperature was measured with three preloaded type K thermocouples. In addition, two thermocouples were applied outside the test cross-section, see Fig. 3. Focus was laid on achieving a homogeneous temperature distribution within the testing area.

Fig. 3
figure 3

Detailed experimental test setup during high temperature test

Full size image

In order to parameterize and validate the material model, in total, ten tensile tests, fourteen LCF, and twelve CLCF tests were performed with specimens machined out of the Ti-6Al-4 V substrate and the built-up WAAM structure. In the first step, ten tensile tests were carried out to investigate the quasi-static behaviour and to estimate the strain levels for the LCF and CLCF tests. Thereby, five test specimens were taken from the substrate and five from the WAAM structure. Two tests were performed at room temperature and one test at each temperature level. Basic boundary conditions for tensile tests, like temperature levels and the strain rate, are shown in Table 2. As mentioned before, specimens were heated inductively, and all tests were carried out in a single-stage, strain-controlled mode until fracture of specimen.

Table 2 Defined boundary conditions of the conducted tests
Full size table

Regarding the material modelling itself, twelve uniaxial CLCF tests had been performed at different temperature levels, see Table 2. Temperature, strain amplitude, and strain rate were defined in consideration of the previously executed tensile test and the usually in WAAM processes occurring values. During these complex LCF tests, the strain rate was varied in addition to the strain amplitude. Furthermore, two holding cycles were implemented in the test programme. Thus, with one test at a defined temperature level, the influence of strain amplitude, the strain rate dependency, and creep or stress relaxation can be evaluated as a basis for further material modelling [28].

In addition, 14 isothermal LCF tests were performed at different temperature levels with varying strain amplitudes to investigate the material behaviour in detail and to validate the model developed.

2.3 Measurements

For validation of the enhanced thermomechanical simulation and comparison with experimental data, a ten-layer structure was manufactured as aforementioned. Additional preliminary measurements were conducted on the substrate, right next to the deposited structure, whereby the residual stress state as well as the distortion were compared to the simulation results.

Residual stress analysis was executed before and after the WAAM process at the same measurement points to determine the difference in residual stress state. In addition to the measurement on the top of the substrate, the measurements were made on the bottom as well, determining the residual stresses in the longitudinal direction, which is parallel to the welding direction. One measurement line at the top of the substrate is shown in Fig. 4, where in total 33 points were measured over a length of 160 mm. A X-RAYBOT from MRX-RAYS was used for the measurements, in which residual stresses were determined by X-ray diffraction. Additionally, distortion in Z-direction was measured contactless with a 3D-scanner ATOS Core from GOM Metrology. For this purpose, the substrate was scanned before and after the additive manufacturing, compared directly with each other to determine the Z-distortion of the substrate. The measured distortion was then compared to the numerical results at the same line where the residual stress was measured, see Fig. 4.

Fig. 4
figure 4

Approximate position of residual stress and distortion measurement line

Full size image

3 Structural simulation with viscoplastic material model

3.1 Simulation model

The fully transient simulation of the WAAM process was performed using the commercial finite element software tool Simufact Welding. For the validation and evaluation of the estimation accuracy of the elaborated material model with experimental distortion and residual stress measurements, a linear, ten-layer WAAM part was set up according to the experimental data. The geometrical boundary conditions, such as the clamping and the dimensions of the structure, were obtained from the experiment, see Fig. 5. For the discretisation of the geometry, a mesh was established using hexahedral elements with an approximate size of 1 × 1 × 1 mm3. The model consists of about 91,700 elements in total, whereby 39,600 were used in the substrate, 50,700 for the structure, and 700 for each clamping. Process times and especially dwell times were set according to the measured process times. The equivalent force and stiffness of the physical clamping were evaluated with a subsequent linear elastic analysis and then implemented as a linear spring in the simulation model. The element activation method was carried out using the quiet element method [29].

Fig. 5
figure 5

Experimental setup and associated geometry in the simulation model for ten-layer structure

Full size image

To simulate the WAAM process, a transient coupled thermomechanical analysis was utilised. In the first step of the numerical analysis, heat transfer analysis was executed, and the temperature field was calculated, followed by the application of the thermal loads to the elasto-viscoplastic mechanical analysis. Basically, this procedure with thermal calculation followed by the mechanical solution was done for each increment.

The governing differential heat transfer equation for the calculation of the temperature field can be written as follows:

$$\uprho {\mathrm{c}}_{\mathrm{p}}\frac{\partial \mathrm{T}}{\partial \mathrm{t}}=\uplambda \left(\frac{{\partial }^{2}\mathrm{T}}{\partial {\mathrm{x}}^{2}}+\frac{{\partial }^{2}\mathrm{T}}{\partial {\mathrm{y}}^{2}}+\frac{{\partial }^{2}\mathrm{T}}{\partial {\mathrm{z}}^{2}}\right)+{\mathrm{q}}_{\mathrm{v}}$$
(1)

where ρ is the density, cp is the specific heat capacity, and λ is the thermal conductivity of the material. The thermophysical material properties ρ, cp, and λ are temperature and microstructure dependent. In this study, a temperature-dependent model for single-phase microstructure was used, according to the material database for Ti-6Al-4 V implemented in the used simulation software Simufact Welding 2021. Additionally, T is the temperature, t denotes the time, and qv denotes the total heat volumetric input from the Goldak model [30]. To solve this governing equation, it is necessary to define a model for heat input and the thermal boundary conditions. For the heat source model, a double-ellipsoid volumetric heat source model according to Goldak was applied, see Fig. 6 [30].

Fig. 6
figure 6

Schematic of double ellipsoid heat source model according to Goldak [30]

Full size image

The volumetric heat input qv is specified by a distribution where it is separated into the front qv,f and the rear part qv,r. The front and the rear volumetric heat inputs are defined as follows:

$${\mathrm{q}}_{\mathrm{v},\mathrm{f}}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)= \frac{6 \sqrt{3} {\mathrm{f}}_{\mathrm{f}}\mathrm{ Q}}{{\mathrm{a}}_{\mathrm{f}}\mathrm{ b c \pi }\sqrt{\uppi }} {\mathrm{e}}^{- \left(\frac{3{\mathrm{x}}^{2}}{{\mathrm{a}}_{\mathrm{f}}^{2}} + \frac{3{\mathrm{y}}^{2}}{{\mathrm{b}}^{2}} + \frac{3{\mathrm{z}}^{2}}{{\mathrm{c}}^{2}}\right)}$$
(2)
$${\mathrm{q}}_{\mathrm{v},\mathrm{r}}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)= \frac{6 \sqrt{3} {\mathrm{f}}_{\mathrm{r}}\mathrm{ Q}}{{\mathrm{a}}_{\mathrm{r}}\mathrm{ b c \pi }\sqrt{\uppi }} {\mathrm{e}}^{- \left(\frac{3{\mathrm{x}}^{2}}{{\mathrm{a}}_{\mathrm{r}}^{2}} + \frac{3{\mathrm{y}}^{2}}{{\mathrm{b}}^{2}} + \frac{3{\mathrm{z}}^{2}}{{\mathrm{c}}^{2}}\right)}$$
(3)

where af, ar, b, and c denote the front and rear length, the width, and the depth of the ellipsoid, presented in Fig. 6. The applied power Q stands for the total power of the heat source, and the variables ff and fr are dimensionless factors. Due to heat losses during the WAAM process, it is necessary to define thermal boundaries to consider heat losses such as convective heat transfer qc, emission or radiation qr, and contact heat transfer qcon. The convective heat loss qc is given as follows:

$${\mathrm{q}}_{\mathrm{c}}=\mathrm{h }\left(\mathrm{T}-{\mathrm{T}}_{0}\right)$$
(4)

where h is the heat transfer coefficient, T is the surface temperature, and T0 is the ambient temperature. Heat loss due to emission or radiation qr can be described with the Stefan-Boltzmann law [31]:

$${\mathrm{q}}_{\mathrm{r}}=\upvarepsilon {\upsigma }_{\mathrm{b}}\left({\mathrm{T}}^{4}{-\mathrm{T}}_{0}^{4}\right)$$
(5)

where ε is the emission coefficient of the surface, and σb is the Stefan-Boltzmann constant. In addition, if the surface of a solid is in contact with another solid, heat transfer due to contact qcon can occur. The contact heat transfer is defined as follows:

$${\mathrm{q}}_{\mathrm{con}}=\mathrm{\alpha }\left({\mathrm{T}}_{1}-{\mathrm{T}}_{2}\right)$$
(6)

where α is the contact heat transfer coefficient, and T1 and T2 are the temperatures of the two contacting bodies. After the solution of the heat transfer analysis and the thermal pass, the elasto-viscoplastic simulation and mechanical pass are executed. The parameters of the Goldak heat source model as well as the values of the thermal boundaries were calibrated in pre-studies [23] by comparison of the simulated temperature field with experimentally measured data from thermocouples.

The main equation for the mechanical pass is the stress equilibrium, which can be expressed as follows:

$$\frac{\partial {\upsigma }_{\mathrm{j},\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+{\mathrm{f}}_{\mathrm{i}}=0$$
(7)

where fi is the sum of body forces, and σ is the second order stress tensor [31]. Regarding the basic material model and plasticity, the hypo-elastoplastic formulation is applied, and strain ε is decomposed as follows:

$$\upvarepsilon ={\upvarepsilon }_{\mathrm{e}}+{\upvarepsilon }_{\mathrm{p}}+{\upvarepsilon }_{\mathrm{T}}+{\upvarepsilon }_{\mathrm{cr}}$$
(8)

with the elastic strain εel, the plastic strain εpl, the thermal strain εT, and the creep strain εcr. This formulation is specified as additive plasticity [29, 32]. In addition to the plasticity in this formulation, a Norton-Bailey creep model was implemented in the WAAM process simulation to take creep effects into account, which is described in [23].

3.2 Viscoplastic material model

In general, a material model was used to describe the physical material behaviour as realistic as possible in the simulation and, hence, also to describe the relationship between stress and strain. In addition to the linear, elastic region, which was described by Hooke’s law, the non-linear region was described and modelled in the course of the plasticity theory. Basically, a material model was formed by the yield function, the flow rule, and the hardening law. The yield function describes whether elastic or elasto-plastic deformation occurs, and the flow rule gives the direction and amount of the plastic strain component. The hardening law describes the change in the yield surface as a result of a stress above the flow limit. If a time-dependent material behaviour occurs during loading, a viscous part was added to the elasto-plastic material model [33, 34].

To consider the strain rate and temperature dependency of Ti-6Al-4 V in the material model, a time dependent, combined, elasto-viscoplastic Chaboche model [35, 36] was chosen. The model parameters were determined based on tensile, low-cycle fatigue, and complex low-cycle fatigue tests. The model consists of a kinematic and an isotropic part and was supplemented by a viscous part to describe time-dependent effects. In general, the isotropic part describes the change of the flow surface size, and the kinematic part describes the translation of the flow surface. The isotropic hardening model, which describes the change in the flow surface size, can be used to model and account for hardening or softening due to plastic strains. The change of the flow limit R as a function of the accumulated plastic strain p is integrally described as follows:

$$\mathrm{R}=\mathrm{Q}(1-{\mathrm{e}}^{-\mathrm{bp}})$$
(9)

where b and Q are material specific constants. Thus, the parameter Q represents the absolute change in the flow surface, and parameter b represents the rate of change [37]. The parameters Q and b were fitted in the course of the material modelling.

The kinematic hardening model describes the translation of the yield surface in the stress space, whereby the size of the flow surface does not change. For the kinematic model, a non-linear approach was chosen:

$$\dot{\mathrm{\alpha }}=\mathrm{C}\frac{1}{{\upsigma }_{0}}(\upsigma -\mathrm{\alpha })\dot{{\upvarepsilon }_{\mathrm{p}}}-\mathrm{D\alpha }\dot{{\upvarepsilon }_{\mathrm{p}}}$$
(10)

where C and D are material-specific parameters, σ is the stress tensor, α the back-stress tensor and \(\dot{{\upvarepsilon }_{\mathrm{p}}}\) the equivalent plastic strain rate. The kinematic hardening model allows the usage of multiple initial functions for the best possible representation of the deformation behaviour [38]. In the course of the material modelling, one back-stress tensor was used for simulation, and the material parameters C and D were fitted using the experimental data.

To consider time-dependent material behaviour, a strain-rate-dependent viscous approach was integrated into the elasto-plastic material model. A power function was used to describe the viscous stress component σvp in the material model as follows:

$${\upsigma }_{\mathrm{vp}}=\mathrm{K}{\dot{\mathrm{p}}}^{\frac{1}{\mathrm{n}}}$$
(11)

where K and n are material specific fit parameter, and \(\dot{\mathrm{p}}\) is the plastic strain rate [34].

The correct fit of the parameters for the selected material model is an essential part of the modelling process. In [39], the applied methodology for fitting the data, which was used in this work, is described in detail. For the fit of the data, it was assumed that the hysteresis has a symmetrical shape in tension and compression. The material model parameters fit by means of the conducted tests were the elastic modulus E, the initial flow limit R0, the isotropic hardening parameter Q and b, the kinematic hardening parameters C and D, and the parameters K and n for the viscous model. For the thermomechanical simulation of the WAAM process, the material model parameters were fitted for each temperature level and then implemented in the simulation as a function of temperature. A linear interpolation of the parameters was performed between the fitted temperature levels.

4 Results

4.1 Experimental results

Initially, the experimental data was examined in more detail, and the elasto-viscoplastic material behaviour of Ti-6Al-4 V was investigated. Furthermore, a detailed comparison was made between the behaviour of the substrate and the WAAM material. The analysis of the LCF tests with respect to the cyclic material behaviour shows that, with a constant strain amplitude, a softening behaviour, both for specimens from the substrate and for specimens from the WAAM structure, can be observed. Exemplary results of two LCF tests, conducted with the same test parameters (RT and εa = 1.2), one test carried out with material out of the unprocessed substrate material and one for WAAM material, are shown in Fig. 7. The maximum stress was constant for the substrate material during the first cycles, then decreases with increasing cycle count, and softening occurs. For the material from the WAAM structure, the maximum stress decreases from the first cycle. In Fig. 7a, the maximum stress σmax over the number of load cycles for the substrate and the WAAM material is presented. Furthermore, a significant difference of the maximum stress at the same strain can be seen between the substrate and WAAM material. The WAAM material showed about 10% lower values compared to the substrate material, and this can be explained by the different microstructure due to the different processing histories. The WAAM material is manufactured by melting a wire and therefore building a different microstructure compared to the unprocessed substrate. If the number of load cycles at specimen failure is compared, it is about 40% lower for the WAAM material than for the substrate material.

Fig. 7
figure 7

Comparison of maximum stress (a) and stress–strain hysteresis at Nf/2 (b) for substrate and WAAM material at RT and εa = 1.2%

Full size image

Figure 7b shows the hysteresis of the LCF tests at the half number of cycles to failure Nf/2 for the two material states. On the one hand, the difference in maximum stress was evident, and on the other hand, the hysteresis of the WAAM material in the linear elastic range shows a lower slope than the substrate material, which is due to a lower modulus of elasticity.

If the temperature-dependent material behaviour of the substrate is compared with the WAAM material, lower maximum stresses can be observed for the WAAM material up to 700 °C applying the same strain amplitude. Above a temperature of 700 °C, no significant difference can be observed between the two materials, see Fig. 8.

Fig. 8
figure 8

Stress–strain hysteresis of substrate and WAAM material at N = 2 different temperature levels

Full size image

4.2 Model validation with experimental results

To verify the estimation accuracy of the fitted material model, simplified simulations were performed with the implemented enhanced material model. Low-cycle fatigue and complex low-cycle fatigue tests were modelled in the course of a single element test and compared with the experimental data of the corresponding tests. This verification was done for WAAM material as well as for material out of the substrate. Figure 9a shows the comparison of the hysteresis of the WAAM material at 700 °C for different strain amplitudes, revealing a sound correlation between the simulation and the experimental data. The influence of the strain rate on the material behaviour can be seen in Fig. 9b. It can be observed that with an increasing strain rate, the maximum stress, at the same strain amplitude, becomes larger. This strain rate dependency can be found for both the WAAM and the substrate material. If the simulated hysteresis were compared with the experimental ones, a sound agreement was observed. Only the simulation with the lowest strain rate shows a slight deviation, which is due to time-dependent relaxation effects.

Fig. 9
figure 9

Comparison of simulated stress–strain hysteresis with experiment for different strain amplitude (a) and different strain rates (b) for WAAM material

Full size image

Finally, to validate and evaluate the estimation accuracy of the elaborated material model, a simple but representative WAAM part was simulated, as introduced in Sect. 3.1. The resulting residual stress state and distortion of the enhanced simulation were then compared to the corresponding experimental data. In Fig. 10, the resulting residual stress in the longitudinal direction as well as the distortion are shown for the validation model.

Fig. 10
figure 10

Overview on simulated residual stress and distortion (five times overdrawn)

Full size image

In Fig. 11, the simulated and measured distortion values are compared. It can be found that the distortion can be determined without significant deviations for a WAAM part under the implementation of the elaborated material model. The simulated maximum distortion shows a small deviation of up to about 6%. In comparison, the distortion with the existing material model shows a significant overestimation of about 60%.

Fig. 11
figure 11

Comparison of simulated and measured distortion of the substrate

Full size image

In addition, the simulated residual stress state was compared to the experimental data at the top and bottom of the substrate, see Fig. 4. In Fig. 12, the residual stress difference, evaluated as a difference before and after the WAAM process, in the welding direction along the substrate (Y-direction) is shown. The comparison in Fig. 12 demonstrates that the numerical estimation of the residual stress state by means of structural simulation and the implemented material model provide good results for the residual stress state of the substrate on the upper and lower side. Both tensile residual stresses on the bottom and compressive residual stresses on the top side were well estimated by the simulation.

Fig. 12
figure 12

Comparison of simulated and measured residual stress difference

Full size image

5 Summary and conclusions

In this study, experimental quasi-static and cyclic tests were performed to evaluate the material behaviour of the titanium alloy Ti-6Al-4 V and to implement an elaborate elasto-viscoplastic material model for the simulation of the WAAM process. Tensile, LCF, and CLCF tests in a wide temperature range, with different strain amplitudes and strain rates were carried out to characterise and parametrize the material model. Comparable material behaviour of substrate and WAAM material was observed by the experimental tests, whereby the WAAM material tends to lower stress values testing at the same strain amplitudes due to a different microstructure. A combined elasto-viscoplastic Chaboche model was applied to fit the experimental data and model the material behaviour. Subsequently, the fitted Chaboche model was implemented in the simulation and validated. Validation was carried out by simulation of a ten-layer WAAM part and comparison of the residual stress state and distortion of the substrate to the experimental data. Based on the conducted investigations and the presented results, the following conclusions can be drawn:

  • An elasto-viscoplastic Chaboche model can be used to describe the material behaviour dependent on temperature, strain amplitude, strain rate of wire arc additive manufactured Ti-6Al-4 V, and for substrate material.

  • By using this Chaboche model for the thermomechanical simulation of the WAAM process, it is possible to estimate the residual stress state and distortion with minor deviations between simulation and experiment.

  • With the presented methodology, the numerical estimation of residual stresses and distortion of complex WAAM parts is thus possible, enabling a further numerical process optimization by parametrically assess the effect of selected WAAM process parameters on the resulting residual stress and distortion condition.

Due to the increasing simulation time for more complex parts, ongoing research is focusing on possible time savings while maintaining as much accuracy as possible. Additionally, in future work, it is planned to validate the material model for industrially relevant WAAM structures using an appropriate reference component or prototype, and a focus will be on the residual stress distribution in transversal direction and in the WAAM structure itself. Moreover, the numerically residual stress state can be incorporated within an existing fatigue design approach for Ti-6Al-4 V WAAM structures [40].