1 Introduction

The L-PBF process allows the manufacturing of parts with complex geometry and is used more and more in the industry, especially in aeronautics, naval, and aerospace fields or in the medical sector. In the last few years, research has largely focused on the mechanical properties and the density of parts produced by L-PBF [1] and less on the dimensional aspect. However, the study of the dimensional accuracy can be crucial for some applications which do not enable machining afterwards. This concerns parts with internal channels, lattice structures, or more generally all parts whose dimensions and geometry do not allow catching up for the errors through post-process steps.

The dimensional accuracy is defined as the compliance with the geometrical and dimensional tolerances (GD&T), according to the standard ISO 1101:2017 [2].

Deviations in the dimensions or the geometry of the final part can have several origins. The geometry and the shape can be altered by distortions due to residual stresses. This can be due to the relaxation of residual stress occurring when the part is removed from the build platform post-process or during the process, if the stress exceeds the yield strength of the material [3, 4]. Residual stresses are introduced into the part during the process due to the incompatibility of thermal dilatation between the heating and cooling cycles, and are accentuated by the important thermal gradients at stake when the powder is melted [5]. Distortions can also be generated by overheating on overhanging surfaces due to the bad thermal conduction provided by the powder underneath the surface that is being heated by the laser [6]. Concerning the deviations on the dimensions, shrinkage occurring after cooling can generate undersizing compared to the computer-aided design (CAD) model [7]. Finally, the width of the weld beads, which are the tracks of the solidified material after the passing of the laser, defines the size of the smallest built element [8]. There also exists other sources of dimensional errors non-process wise such as the errors related to the Standard Tessellation Language (STL) file or to the slicing step [9, 10].

There is a wide range of variable parameters in the L-PBF process that can have an influence on the described above phenomena. For instance, it has been shown that the laser power, the scanning speed, and the volumetric energy density (VED) have a significant impact on the residual stress [5], on the shrinkage [7], on the width of the beads [11, 12], and more generally on the dimensional errors [13]–[15] of manufactured parts. However, other process parameters can also affect the manufacturing. Indeed, residual stress can be induced by the length of the scan tracks [16], by the layer thickness, or by the orientation of the part on the build platform. Concerning the overheating, it can be reduced with a relevant choice of supports [17] helping the thermal exchange through conduction or with an orientation avoiding sharp angles of the part with the build platform [18].

As the pre-cited distortions and dimensional errors are related to thermic and heat exchanges, it has been decided for this study to focus on this aspect in order to better understand the mechanisms at the origin of the dimensional deviations of the parts. To do so, an infrared (IR) camera has been instrumented in situ, allowing to monitor the temperature during the manufacturing of thin wall parts made in Inconel 625, similarly to what has been done in other studies [19, 20]. To analyze the thermal data, thermal parameters in the form of a thermal gradient, temperature, and characteristic times associated with the cooling rate were then defined in order to quantify and compare the thermal state of the different walls. Parts were manufactured with variation of nominal dimensions and process parameters (laser power and scanning speed) for the filling and contour steps. The wall shape for the parts has been chosen because of its simple geometry, easy to characterize, and often used for dimensional accuracy studies [16, 21]. Concerning the process parameters, it has been decided to concentrate on the influence of the laser power and scanning speed, as those parameters seem to be the reason for the majority of the dimensional and geometrical deviations, as well as the nominal dimension to evaluate the impact of the size of the heated zone. The walls were then measured with a coordinate measuring machine (CMM), similarly to other studies [14, 22], in order to establish the correlation between the thermal and the dimensional and geometrical deviations.

In the following paper, the procedure followed to generate the experimental thermal data will be firstly presented, then the method used to determine the thermal parameters will be addressed. Finally, the analysis of the results of the thermal parameters and of the dimensional and geometrical characterization will be displayed, as well as the correlation between these two.

2 Materials and method

2.1 Experimental procedure

The L-PBF machine used is a 3DSystems ProX DMP320 equipped with a polymer scraper and an f-theta lens enabling the laser to have its focal point on the powder bed. The laser is an ytterbium fiber laser, with a spot diameter measured to be 70 µm and a wavelength of 1070 nm. Argon is used as inert gas with a flow rate of 50 cm3/s. No preheating is performed on the build tray. The alloy used is Inconel 625, provided by LPW Technology, with a powder distribution centered around 32.15 µm. Inconel 625 is a nickel-based superalloy often used in the industry due to its good weldability, resistance to corrosion, and mechanical properties even at high temperatures [1]. Its main thermo-physical properties are detailed in Table 1, where the properties are given at 25 °C when they are not referring to a temperature.

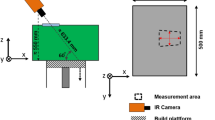
Table 1 Thermo-physical properties of the Inconel 625
Full size table

The manufactured parts are thin walls with variable thicknesses, 30 mm high and 20 mm wide, with a supporting block which consists in a 5 mm high pad added underneath the wall. Supports were also disposed underneath the parts in order to remove easily the parts from the build platform (Fig. 1). Concerning the process parameters, variations have been made on the laser power and scanning speed of both filling and contour steps, in order to have variations of VED (Table 2). The VED, in J.mm−3, is defined as as follows:

$$\mathrm{VED}=\frac{P}{v\Delta hH}$$
(1)

with P the laser power in W, v the scanning speed in mm.s−1, Δh the layer thickness, and H the hatching space, both in mm. The layer thickness is 0.06 mm, and the hatching space is 0.1 mm. The time between each recoating of powder is by default fixed at 12 s. The scanning strategy consists of a filling step with back and forth tracks spaced apart by a hatching space of 100 µm and two contour steps with the same hatching space. For the tracks of the filling step, there is an angle rotation of 65° between each layer. Variations have also been made on the nominal dimension, i.e., on the thickness of the walls, as detailed in Table 2. The choice of the parameters was established as variations around the standard set of parameters “Std,” which are the ones recommended by the machine manufacturer 3DSystems. One part per set of parameter was manufactured, resulting in a total of 10 parts.

Fig. 1
figure 1

Photo of the manufactured platform

Full size image
Table 2 Process parameters used for the manufactured parts
Full size table

The parts have been designed on the software Solidworks and exported as STLs, while the preparation (nesting, supports, scanning strategy) of the batch has been performed on 3DExpert. The laser power and scanning speed were entered in the software DMP Control.

The camera implemented in the L-PBF machine is a FLIR X8500sc IR camera with a resolution of 1280 × 1024 pixels and a frame rate of 180 images per second, allowing to record the temperature of the parts during the process on the last deposited layer. Beforehand, the camera has been calibrated in temperature by the distributor on black bodies. It is instrumented in situ (Fig. 2), with a restricted observation range due to its position in the build chamber, allowing a small build platform, with an effective surface of 10 × 10 cm2. The optical filters chosen for the camera define the range of the recorded temperatures between 107 and 889 °C, as the emissivity chosen in the conversion from the radiation to the temperature was 0.4 [24]. Acquisitions were performed at three different heights of construction: 16.5 mm, 22.8 mm, and 30 mm, arbitrarily chosen to characterize the evolution of the thermal characteristics during the process. At each height, the recording lasted for three consecutive layers, to ease the data treatment and due to the large size of the generated files.

Fig. 2
figure 2

Instrumentation of the IR camera inside the build chamber of the L-PBF machine

Full size image

The software used as an interface between the camera and the computer is ResearchIR. It returns the average temperatures on a region of interest (ROI), which has been chosen to be a line shape for the study of the walls (Fig. 3). In the end, a “.csv” file with the temperature versus time for the different process parameters was extracted.

Fig. 3
figure 3

Screenshot of the analyzed walls observed through the IR camera during the process, with line ROIs

Full size image

It may seem in Fig. 3 that the powder surrounding the solid material is hotter. It is due to the higher emissivity of the powder, which is not fully dense and generates multiple reflections, compared to the solidified material. This phenomenon falsifies the returned temperature values of the surrounding powder.

The CMM used to characterize the dimensional accuracy is an UPMC Carat by Zeiss, equipped with a 3 mm diameter sensor probe in ruby. The parts were measured as built after being removed from the platform, without any heat treatment or other post-process step, in order to take into account the eventual distortions due to residual stress. On each wall, the thickness of the wall and its flatness were determined. The thickness is defined here as the distance between a probed point and the Gaussian plane of the opposite face of the wall. The displayed value for thickness evaluation is the averaged absolute error of 9 probed points over each face of the wall, i.e., 18 points. The flatness is the distance between two parallel planes that contain all of the analyzed surfaces, which is determined by probing 20 × 10 points on each face. The error bars displayed in the results representing the standard deviation for the different measurements of the thickness and the flatness of the walls are symmetrical. If the error bar is not visible for a data point, it means that it is small enough to be hidden by the marker. All of those measurements were performed according to the standard ISO 1101:2017 [2].

2.2 Determination of the thermal parameters

The objective of the study is to correlate the thermal phenomena with the dimensional accuracy of the L-PBF as built parts. As the residual stresses, which create distortions, are resulting from high thermal gradients, it is important to be able to quantify the heating phase as well as the cooling rate. The thermal gradient for the heating phase ΔT is defined here as the gap in temperature for the part between the recoating and the peak following the melting. Also, the temperature of stabilization Ts is defined as the temperature of the part measured by the IR camera just before the recoating of the powder. It gives information about the heating of the part during the process. However, as Fig. 4 shows, the cooling of the parts is obviously non-linear, which makes the analysis of the cooling rates and their comparisons between the different process parameters difficult. Therefore, a method is needed to extract a meaningful scalar from the curves—here a characteristic time (in seconds)—which represents how fast the part is cooling. The approach chosen has been to fit a simple thermal model, described below. It allows obtaining coefficients that are easy to compare, while maintaining a physical sense so that the results remain coherent without having to model the process with finite elements.

Fig. 4
figure 4

Plot of the temperature versus time (T = f(t)) for two sets of process parameters, during three consecutive layers, where 1. is the “Std” set of parameters, and 6. is the set of parameters with low energy

Full size image

The fitted function is derived from the heat equation [26]. It takes into account a heated zone, which is the zone heated by the laser, at a temperature T(t) measured by the IR camera and the underlying zone at a temperature Tu(t). The heat exchanges considered are convection between the heated zone and the atmosphere and conduction between the heated zone and the underlying zone (Fig. 5).

Fig. 5
figure 5

Scheme of the heat exchanges in the wall taken into account for the heat equations

Full size image

To state the equations, thermal conduction with the powder on the sides of the part as well as conduction with the build platform are neglected. These assumptions have been made because the surface of contact between the supports and the bottom of the part is less than 5% and because the thermal conductivity of the powder is 20 times smaller than that of the solid material [27]. Also, it is assumed that the temperatures are homogenous within the two zones. Lastly, the heat equation on the heated zone (Eq. (2)) and the heat equation on the underlying zone (Eq. (3)) are carried on the mass, giving the following:

$$m{C}_{p}\frac{\partial T}{\partial t}={-k}_{v}\left({T-T}_{atm}\right)S-{k}_{c}\left(T-{T}_{u}\right)S$$
(2)
$${m}_{u}{C}_{p}\frac{\partial {T}_{u}}{\partial t}=-{k}_{c}\left({T}_{u}-T\right)S$$
(3)

with m the mass of the heated zone and mu the mass of the underlying zone, both in kg. T is the temperature of the heated zone, Tu is the temperature of the underlying zone, and Tatm is the temperature of the atmosphere (Ar gas) which are all three in kelvin (K). Cp is the heat capacity in J.kg−1.K−1. The heat exchange coefficient for the convection is kv, and the heat exchange coefficient for the conduction is kc, both are in W. m−2.K−1. Finally, S is the surface of exchange, which is the same for both equations, in m2. The ratio of mass between the heated and the underlying zone is represented by a constant factor K, such that K × m = mu. By dividing each side of the equations by the volume of the heated zone V (in m−3), noticing that V = l × S, with l the length of the heated zone in meter (m), the Eqs. (4) and (5) are obtained:

$$\frac{\partial T}{\partial t}=-\frac{1}{{h}_{v}}\left({T-T}_{atm}\right)-\frac{1}{{h}_{c}}\left(T-{T}_{u}\right)$$
(4)
$$\frac{\partial {T}_{u}}{\partial t}=-\frac{1}{{h}_{c}\bullet K}\left({T}_{u}-T\right)$$
(5)

where hc and hv are defined in the Eqs. (6) and (7), both in second (s), which are respectively the characteristic times for convection and conduction used in this study for the comparison between the process parameters. ρ is the density in kg.m−3.

$${h}_{c}=\frac{\rho {C}_{p}l}{{k}_{c}}$$
(6)
$$h_v=\frac{\rho C_pl}{k_v}$$
(7)

To simplify the resolution, it is assumed that the characteristic times vary according to the constructed height, but not with the temperature, even though in reality it is known that ρ, Cp, and the heat exchange coefficients vary with the temperature. Thus, according to the formulation of the equations, if the characteristic times hv or hc decrease, it means that the cooling rate gets higher and therefore that the temperature is dropping faster.

In the end, the explicit Euler method [28] has been used to obtain the function T(t) from the coupled differentials Eqs. (3) and (4). Numerical resolution has been chosen because the analytical resolution is not feasible. The time step is considered to be the time resolution of the camera: 0.016 s. T(t = 0) is the peak temperature preceding the cooling, and Tu(t = 0) is approximated as the temperature of stabilization for the analyzed layers, noted Ts, taken as the temperature of the part before the recoating of the powder. hv, hc, and K are the parameters to fit through least square method in order to minimize the differences with the experimental data. Several functions T(t) are hence iteratively computed until the best set of parameters hv, hc, and K is found.

After performing the fit on the experimental data, the returned values which are analyzed in the study are the characteristic times hv and hc, as well as the temperature of stabilization Ts and the thermal gradient for heating ΔT. All of these are averaged on three consecutive layers for each analyzed height of construction, and the error bars found on the results of thermal parameters represent their standard deviations on the three layers. Figure 6 shows an example of experimental data, with the fitted curves for the cooling steps.

Fig. 6
figure 6

Plot of the temperature versus time (T = f(t)) for a set of experimental data and its fitted temperature for the cooling steps

Full size image

In order to understand better the meaning of hv and hc and their impact on the cooling rate, Figs. 7 and 8 display the temperature versus time after a peak of temperature, for variations of one characteristic time while the other remains constant. These cooling curves are generated from Eqs. (4) and (5), with the typical values for hv and hc encountered in the following study. Therefore, the hv values are around 3 s while the hc values are around 0.3 s. It is interesting to note that the characteristic time for conduction is drastically lower than the one for convection, which is coherent as the heat transfer by conduction should be higher than the one by convection, with the thermal properties involved.

Fig. 7
figure 7

Plots of T = f(t) for different values of hc, with hv = 3 s

Full size image
Fig. 8
figure 8

Plots of T = f(t) for different values of hv, with hc = 0.3 s

Full size image

Basically, it is possible to consider the cooling rate curve as composed of two sections with two different slopes. The first slope, the most abrupt one, may be the origin for residual stress, as it is the steepest one. The second slope can be attributed to a thermal drift. Thus, it can be seen that variations of hv in the order of 1 s with constant hc will only affect the second slope value, which decreases when hv increases, resulting in a lower final temperature. Concerning hc, it seems that little increase in the order of 0.2 s shifts the inflection point of the curve further in time and toward lower temperatures. This causes important decreases in the first slope, which goes from 1100 °C/s with hc = 0.1 s to 350 °C/s for hc = 0.5 s. This indicates that lower values for hc will increase the cooling rate, which is supposedly responsible for the residual stress generation.

The influence of the maximum temperature, and thus of ΔT, with constant characteristic time has also been observed (Fig. 9). The two slopes remain similar but the amount of time during which the first slope is maintained increases when ΔT increases, which can be assimilated to the time during which residual stress will be generated in the heated zone.

Fig. 9
figure 9

Plot of T = f(t) for different values of maximum temperatures

Full size image

3 Results and discussion

3.1 Influence of the number of contour

The characteristic times for convection and conduction of walls with one or two contour steps are displayed in Fig. 10. It appears that using one or two contour steps does not seem to change significantly the thermal parameters. Also, the influence of the height of construction is not clear enough to be considered. Therefore, the next parameters studied will only be displayed for the last three layers recorded, at 30 mm of height.

Fig. 10
figure 10

Influence of the number of contour on a) the characteristic time of convection hv and b) the characteristic time of conduction hc, for different heights of construction

Full size image

3.2 Influence of the dimension

The thermal parameters for walls with variable thicknesses are displayed in Fig. 11. There is a clear correlation between the thickness of the wall and the thermal parameters. The temperature Ts, and the characteristic times of convection hv and conduction hc are increasing linearly with the dimension. The thermal gradient ΔT is decreasing with the increase in thickness. This means that the thinnest wall with 0.5 µm thickness has the highest thermal gradient ΔT above 425 °C, as well as the fastest cooling rate resulting from a low value for hc around 0.3 s, while keeping a lower temperature of stabilization due to the lower value of hv. It should be noted that the large error bars on ΔT could come from the steepness of the rise in temperature during the heating of the part, which can lead to variations in the measured peak temperature. This is because of the framerate of the IR camera that may skip the real peak temperature. This is applicable to all of the parts.

Fig. 11
figure 11

Influence of the nominal thickness on a) the temperature of stabilization Ts, b) the thermal gradient for heating ΔT, c) the characteristic time of convection hv, and d) the characteristic time of conduction hc

Full size image

The analysis of the thermal parameters indicates that the thinner the wall is, the faster it cools down both by conduction and convection. Surprisingly, thinner parts endure more severe thermal gradients for the heating phase. Also, the fact that thicker parts cool down more slowly than thinner parts may result from a thermal inertia due to a larger mass for the two zones, and thus with a greater proportion of heat stored in the underlying zone. Indeed, if the difference of temperature between the underlying zone and the heated one is lower, the heat exchanges by conduction will be reduced.

As Fig. 12 shows, the part that displays the highest geometrical distortions is the 0.5 mm thick wall. The flatness value of almost 100 µm is due to the bowing of the part (Fig. 13a). This bowing could be due to the residual stress relaxation, which has to be higher for this part because of more important cooling rate and thermal gradients, as the values of hc = 0.3 s and ΔT = 430 °C reveal. No other part displays bowing in the same way as the 0.5 mm thick wall. In fact, the flatness errors encountered for every other part are due to roughness, similarly to the flatness profile shown in Fig. 13b. The distortions occur for thickness between 0.5 and 0.7 mm (Fig. 14), which must mean that the yield stress was exceeded for the concerned parts.

Fig. 12
figure 12

Influence of the nominal dimension on a) the absolute error on the thickness of the wall and b) the flatness of the wall

Full size image
Fig. 13
figure 13

Representation of the flatness measured on one face of the wall for a) the wall with a thickness of 0.5 mm and b) the wall with the thickness of 1 mm, with an amplification factor of 300, where z is the building direction

Full size image
Fig. 14
figure 14

Influence of the filling VED on a) the temperature of stabilization Ts, b) the thermal gradient for heating ΔT, c) the characteristic time of convection hv, and d) the characteristic time of conduction hc.s

Full size image

Concerning the influence of the dimensional accuracy on the thickness, the absolute errors are all positive and around 30 µm, except for the wall of 0.5 mm thickness. The latter has a lower absolute error, but the dispersion of the results is greater because of the bending of the part, degrading the measurements. It seems that there is no influence of the nominal dimension on the dimensional accuracy. However, a 30 µm error on a 0.7 mm thick wall represents a relative error of 4% which can be problematic depending on the wanted application. More generally, it seems that the thickness and flatness measurements follow asymptotic trends (Fig. 15), but the amount of data available is not sufficient to conclude on this.

Fig. 15
figure 15

Influence of the filling VED on a) the absolute error on the thickness of the wall and b) the flatness of the wall

Full size image

3.3 Influence of the laser power and scanning speed

The thermal parameters for walls manufactured with variations of VED obtained through variations of the laser power and scanning speed, for the filling and for the contour steps, are displayed respectively in Figs. 14 and 16. The first thing that is possible to see is the fact that the laser power has an impact on Ts and ΔT for the walls. The influence of the laser power on hv and hc is less significant, and hc goes from 0.51 to 0.4 s when increasing the scanning speed from 900 to 1875 mm/s. It seems that the energy for the filling step has a more significant impact on the thermal parameters than the contour step. Variations when increasing the scanning speed of the contour steps are nonetheless visible on hc, which becomes shorter (Fig. 16).

Fig. 16
figure 16

Influence of contour VED on a) the temperature of stabilization Ts, b) the thermal gradient for heating ΔT, c) the characteristic time of convection hv, and d) the characteristic time of conduction hc

Full size image

Concerning the dimensional accuracy, the errors are comprised between 15 and 35 µm. It seems that the deviations tend to be higher when increasing the laser power and thus the VED for the contour step (Fig. 17a), while it is the contrary when increasing the laser power for the filling step (Fig. 15a). This leads to think that the variations in thickness are certainly due to changes in the bead width with the energy density. Indeed, for the contour step, increasing the VED results in an increase in the measured thickness and can be correlated with the bead dimension variations which follows the same evolution with the VED [12]. For the filling step, ΔT is 50 °C higher for the part with 350 W laser power and 900 mm/s scanning speed, but its thickness decreases compared to the part with 253 W (Fig. 14b). Maybe the denudation, which is more present at high laser power [29], prevents the powder to agglomerate on the surface of the part, as the filling step is performed before the contour, which removes the surrounding powder on the edge of the part.

Fig. 17
figure 17

Influence of the contour VED on a) the absolute error on the thickness of the wall and b) the flatness of the wall

Full size image

The flatness results are between 35 and 50 µm, and there is no distortions. As it has been stated in the previous part, the flatness results are directly related to the roughness if no distortions are visible. It appears that the flatness value gets higher when increasing the VED for contour (Fig. 17b). This might be due to the agglomerates of powder and the generation of spatters that are more present for higher density of energy, thus increasing the roughness [30] and the measured flatness (Fig. 18a), whereas a lower energy for the contour reduces this phenomenon [31].

Fig. 18
figure 18

Representation of the flatness measured on one face of the wall for a) the wall with a high contour energy and b) the wall with a low contour energy, with an amplification factor of 300, where z is the building direction

Full size image

However, the flatness is established in the standard as the distance between two parallel planes allowing to contain all of the measured surface. Hence, it is highly sensitive to local variations, as it is the distance between the lowest and the highest point on the surface which gives the flatness value. Thus, even though spattering is favored by high energy, the presence of a single spatter particle, which can reach the size of 100 µm and is not easily remelted when the laser passes over [32], could be the determining factor for the flatness. This appears clearly in the flatness representation of the wall with lower contour energy (Fig. 18b), which seems less rough than the wall with normal contour energy (Fig. 13b), but has a higher measured flatness. This phenomenon can also explain the sometimes large error bars on the flatness results. Nevertheless, it would be interesting to have a larger amount of sets of parameters in order to confirm the trends that are observed here, for the thermal parameters as well as for the dimensional accuracy.

The thermal parameters for two sets of process parameters with the same VED, but with different laser power and scanning speed are also displayed in Fig. 14. The values are close for the two process parameters, but the one with higher laser power and scanning speed seem to have a slightly lower hv, meaning that the thermal drift makes the temperature drop lower. However, this is compensated by the fact that ΔT is higher, explaining why Ts is the same for the two process parameters. This difference of behavior could come from the angle of the vapor plume—coming from the vaporization of the metal during heating—with the laser beam, which would be higher for the wall manufactured with higher scanning speed. Indeed, the fact that the vapor plume is more directed toward the back of the melt pool generates less absorption from the laser by the metallic vapor, resulting in more energy being absorbed and therefore a higher peak temperature [33].

This is also the cause of the higher error flatness for the set of parameter with 400 W laser power (Fig. 17b), as there are more recirculating movements in the melt pool with higher laser power and scanning speed, inducing more spattering [34]. Concerning the dimensional accuracy, it seems that there are no differences between the two sets of parameters (Fig. 17a).

4 Conclusion

In this study, walls in Inconel 625 have been manufactured with an L-PBF machine instrumented with an in situ IR camera, allowing to follow the temperature of the last layer during the process. Several walls, with thicknesses between 0.5 and 1.5 mm, were manufactured with various laser powers and scanning speeds for both the filling and the contour steps. A numerical method through least square fitting has been established to analyze the thermal data coming from the IR camera for the cooling phase by defining characteristic times hv for convection and hc for conduction. Combined to other thermal parameters known as the temperature of stabilization Ts and the gap in temperature ΔT, the study enabled to identify the influence of the process parameters and nominal dimensions on the thermal gradients endured by the part during the manufacturing process. Then, the study allowed the correlation between the process parameters, the thermal parameters, and the geometrical and dimensional properties—by the mean of respectively flatness and thickness—of those walls, which were measured with a CMM.

Generally, the temperature of the walls at the end of the manufacturing is around 140 °C and increases by more than 350 °C just after the melting. The characteristic time for cooling by conduction hc is the one controlling the most severe slope of the cooling curve, probably at the origin of residual stress, while the characteristic time for cooling by convection hv rather controls the thermal drift.

The thickness has a clear influence on the thermal gradient for the heating phase and on the cooling rate, which are both higher for thinner parts. The thinnest wall of 0.5 mm thickness is the only one that displays distortions that are characteristic of residual stress relaxation and is also the part that endured the most severe thermal gradient and cooling rate, as it has respectively the highest ΔT above 430 °C and lowest hc around 0.3 s. It is characterized by a flatness error of around 95 µm, controlled by the bending of the wall. It is the combination of a high temperature and low hc that generates distortions, as no other part had at the same time a ΔT value above 400 °C and an hc under 0.35 s. However, from 0.7 mm upwards, no influence of the dimension has been observed on the dimensional accuracy or the flatness.

The number of contour has little to no influence on the thermal parameters.

Walls display dimensional errors on the thickness comprised between 10 and 65 µm, and flatness values comprised between 30 and 60 µm, excepted for the 0.5 mm thick wall, which has a flatness of 95 µm.

Variations in the energy density of the filling step have more impact on the thermal parameters than variations on the contour step, whether it be the temperature or the characteristic times. The absolute error on the thickness of the wall increases with the energy density; however, its influence on the flatness has not been clearly determined. The reason is that the flatness values are all due to the roughness and are sensitive to local variations, such as spatters, due to its definition in the standard.

For further research, it will be interesting to manufacture walls with a 0.5 mm thickness at lower energy density in order to see if the distortions are reduced, as the thermal gradient and cooling rate would be less than the one observed in this study. Finally, it appears crucial to measure the residual stress on the walls, by X-ray diffraction (XRD) or hole drilling method, to assess their influence on the results observed in this study.