1 Introduction

Additive manufacturing (AM) of metal components is gaining interest in a variety of industry sectors. The motivation for investigating AM is the potential for manufacturing of components with low geometric restrictions at optimal material usage [2]. However, all DED-processes for AM of metal need to heat the feed material above melting temperature in order to guarantee mechanical performance and leakage tightness [3]. Next to metallurgical phenomena [4], the molten material will always affect the surface of the as-build component. In specific applications, the manufacturers can assure a removal of the primary surface topography by milling, e.g., when AM is used to fabricate near-net-shape components. In other scenarios, for instance when hollow members are manufactured or other geometric restrictions apply, the surface must remain unprocessed. This is also to be expected when cost-sensitive applications, e.g., in the construction industry, are addressed. The unprocessed surface topography of AM components affects the component behavior under mechanical loading and acts as local stress raiser. Cracks will then start propagation from the surface [5]. As a result of the novelty of AM processes for metal, the existing evaluation concepts and quality measures for surface topography of conventionally manufactured metal parts need to be re-approved and further developed. This work demonstrates a possible transfer of methods for fatigue strength estimation from fusion-welded to additively manufactured components.

1.1 AM of metallic components

A large variety of processes is available for AM of metals [6]. The process chain for these methods is basically identical. Starting from a digital CAD-file, which is generated either by a 3D design or a 3D scan, the component is divided into defined layers (“slicing”) to be manufactured in a layer-by-layer approach. The processes relevant for AM of metals are from the categories according to ISO/ASTM 52900 [7]:

  • • Powder bed fusion (PBF),

  • • Direct energy deposition (DED) and

  • • Sheet lamination (SHL).

In the context of AM of metals, the layer height for PBF varies between 20…100 µm and for DED between approximately 1…3 mm. With adapted special technology, the limits can be extended upwards and downwards by approx. 50% in each case [8].

The most widely used welding process in joining technology, gas metal arc welding (GMAW), is frequently used for DED. The energy source for melting feed material is the electric arc (DED-arc). Apart from the commonly used energy-reduced or deposition-controlled arc, the equipment technology remains unchanged. In addition to the use of an established welding process, filler materials familiar from fusion welding were mostly used to date. This enables transfer of process and material knowledge from fusion welding to AM. Depending on the density of the filler material, the geometry of the AM component, and the cooling condition, deposition rates up to 4.5 kg/h (steel) are possible [8]. DED arc has been studied for several applications, for example in the aerospace [9], the automotive [10, 11] and the marine [12] sector. In the last years, the focus of ongoing research work changed from basic feasibility studies into the production of complex components. This included research into material behavior in the area of microstructure, isotropy behavior, and analysis of the mechanical technological quality values of the machined “ideal test specimens” [13]. The current research trend is aimed at analyzing the partially unprocessed additively manufactured components in realistic load conditions. On the part of the German Materials Society (DGM), the following focal points are being set:

  • • Surface quality and fatigue of AM components

  • • Prediction/optimization of surface quality

  • • Surface treatment as well as heat transfer properties of surfaces in additively manufactured thermal systems.

Taking up these focal points, the influences of the surface properties of components manufactured by means of DED-arc are systematically investigated within the article.

1.2 Fatigue of weld metal and metallic AM components

Fatigue of weldments is well understood nowadays. In general, cracks initiate from locations of highest mechanical load and lowest material resistance. Accordingly, mild notches and homogenous microstructure are preferred for high fatigue resistance. The meaning of manufacturing quality for the resulting fatigue strength was emphasized by manifold investigations [14,15,16,17,18] and a guideline for fatigue design was implemented by the International Institute of Welding [19]. Design procedures for weldments are available [20,21,22] and are constantly further developed. Local approaches for fatigue design of welds make use of local load parameters reflecting quality aspects and are well established today. The notch stress approach with reference radii [23, 24] is recommended for weldments with a certain minimum stress concentration [25] and may result in non-conservative results in case of mild notches. For such mild notches, effective stress approaches are available. The stress averaging approach [26] is established on a finite-element-model reflecting the real surface geometry. The effective stress is determined by averaging of the stress σ(x) over a certain microstructural length ρ*. The averaging length is dependent on the material’s support effects. However, a value of ρ* = 0.4 mm and a design S–N curve FAT160 (determined for analyzing maximum principle stress) are considered conservative for welded steels [27].

$$\sigma_{\mathrm{eff}}=\frac1{\rho^\ast}\int_0^{\rho^\ast}\sigma\left(x\right)dx$$
(1)

Although the reference radii approach was not recommended for mildly notched weldments, it was applied successfully to DED-arc specimens before [1]. The authors manufactured and tested DED-arc specimens made from conventional filler material G3Si1 (EN ISO 14341) with un-processed surfaces. The surface was characterized regarding its roughness and the resulting fatigue strength was correlated with the maximum roughness parameter. Additionally, the experimental data was expanded by numerical analysis of randomly generated specimens. A design S–N curve FAT755 was derived, when applying a reference radius of 0.05 mm.

Internal defects in the metallic bulk material may be evaluated by a combined Murakami approach, as demonstrated for laser powder bed fusion material [28]. This approach can also be expanded to surface defects and the interaction of stress raining surface features and internal defects [29]. Based on a knowledge about the defects of AM metal, fracture mechanics may be applied as well [30].

1.3 Surface characteristics resulting from the DED-arc process

The surface topography of DED-arc components shows a mixed deterministic and stochastic nature with strong dependence on the manufacturing parameters [31]. The layer-by-layer building approach results in surface waviness parameters in the mm-range. The process parameters wire feed, corresponding current and voltage, and travel speed determine the melt bead size to be deposited. High energy input results in larger melt beads which are reflected by a larger waviness of the surface after solidification, accordingly. Next to this, the melt metal viscosity and the solidification temperature range are of large importance for the resulting surface topography.

Additional influencing factors are the deposition pattern and the building position. The local bead geometry is influenced by forces acting on the molten zone, namely the arc force, electromagnetic forces, gravity, and forces from chemical reactions in the melt. Especially significant for the surface topography are gravity and the arc force, which act differently on the melt bead depending on the working position and the torch angle. In vertical position, the melt pool is beneficially supported by previously deposited layers. However, due to process restraints of the DED-arc method and complex component geometries, other working positions cannot be always avoided. A multi-scale analysis of surfaces was recommended due to the wide spread of geometric features on surfaces of AM components [32]. The analysis should ideally account deviations from form to roughness. The need for a geometric description of the geometry of AM parts was highlighted earlier [33]. The currently applied standards for surface topography analysis ISO 4287 and ISO 4288 probably need to be revised for description of AM surfaces [34].

2 Experimental and numerical approach

Specimens were manufactured under variation of the building position in order to investigate its effect on the surface and the resulting fatigue strength. The set manufacturing parameters (wire feed, characteristic curve, welding torch travel speed, feed material, interpass temperature) were kept constant during all experiments. Accordingly, the effect of gravity on the surface topography was separated from other manufacturing parameters, which usually affect the microstructure or melt bead geometry.

2.1 Specimen manufacturing

The experimental setup used is shown in Fig. 1. The torch of the welding power source (type Fronius TPS500i) was mounted on a 6-axis handling robot (type Kuka KR22) and moved over a tilt-turn table holding the specimen. The interpass temperature was controlled by a pyrometer (type Dias Pyrospot DGE 44 N) which measured the temperature on top of the last deposited layer. The interpass temperature was kept constant at 200 °C. Cooling time between deposition of subsequent layers was accelerated by application of compressed air. The flow rate was 12 m/s. As shown on the right hand side of Fig. 1, the specimens were manufactured under variation of the inclination of the tilt-turn table. The welding torch was also inclined and kept in line with the specimen building direction.

Fig. 1
figure 1

Experimental setup for the DED-arc manufacturing of specimens (left) under 0° and 75°inclination (right)

Full size image

The feed material used was a low-alloyed high strength wire electrode (type Böhler 3dprint AM80HD) with a diameter of 1.2 mm. The nominal chemical composition is provided in Table 1. The nominal mechanical properties according to the material supplier are listed in Table 2.

Table 1 Chemical analysis of the used filler wire Böhler 3dprint AM80HD
Full size table
Table 2 Mechanical properties of Böhler 3dprint AM80HD according to manufacturer specifications
Full size table

The manufacturing parameters applied are listed in Table 3. In addition to set values, the current I, voltage U, and wire feed speed vwire were measured during the process (type HKS WeldScanner), mean values were determined and the energy input was calculated. Although the set parameters were the same for all four specimens, the resulting energy input varied between 2.3 and 2.7 kJ/cm, which was explained by slight variations of the contact tip distance between tool and work piece.

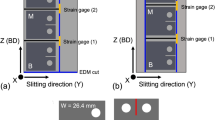
Table 3 Parameters used for the manufacturing of the fatigue test specimens
Full size table

The four specimens (two at vertical position 0° and two at vertical position 75°) had dimensions of 350 mm length and approximately 160 mm height. In total, 82 to 88 layers per specimen were deposited resulting in a layer height of approximately 1.9…2.0 mm. The specimen’s geometry is shown in Fig. 2. Six fatigue test coupons, two benchmark coupons for surface topography investigations, and one metallographic coupon were gained from each specimen. In total, twelve fatigue test coupons were available from each building position. The decision to manufacture two specimens in each building position was made because of the restricted length when printing specimens. In addition, this proved the repeatability of the experiments.

Fig. 2
figure 2

Geometry of DED-arc specimen and location of test coupons for metallography and fatigue testing

Full size image

The surfaces topography of all 24 DED-arc fatigue specimens were analyzed in the as-manufactured state, after water jet cutting. All test specimens were investigated by means of the laser triangulation method (type Micro-Epsilon optoNCDT1800) on both sides along a measuring line located in the middle of the specimen in building direction. The laser diode emits laser light with a wavelength of 670 nm (visible/red) with a spot size of 45 µm at focal position at a resolution in vertical z-direction of 2 µm. The data point distance in scanning direction was 50 µm. Figure 3 shows examples of surface scans from specimens manufactured in vertical (0°) and horizontal (75°) position determined from benchmark coupons. However, the surface waviness of the fatigue test coupons was evaluated at a length of 108 mm. The acting gravity caused distinct surface waviness in dependence of the working position. Both sides of the specimens manufactured at 0° showed similar topography profiles, while the bottom and top side of specimens built in 75° inclination varied clearly.

Fig. 3
figure 3

Exemplary surfaces of specimen manufactured in vertical (0°) and horizontal (75°) position. Left: Surface topography from laser scanning (0°); middle: Photographs of specimens; right: surface topography from laser scanning (75°)

Full size image

In addition to fatigue test experiments, one specimen of similar dimensions was manufactured at constant parameters for tensile tests of the as-deposited material. Specimens were manufactured and milled to a constant thickness of 3 mm from both sides (specimen type E, DIN 50125). The tensile strength of the material in building direction (perpendicular to the layer structure) was Rp0.2 = 710 MPa, Rm = 887 MPa, A = 17.5%, Fig. 4. In comparison to the nominal values provided by the manufactures, the applied building parmeters caused lower values resulting from the interpass temperature applied. A full overview on tensile properties was published earlier [35].

Fig. 4
figure 4

Stress–strain diagram of specimens extracted vertically to the building direction (vtravel = 25 cm/min; vwire = 2 m/min; IPT = 200 °C; active cooling by compressed air). Specimen was manufactured in vertical position (0°)

Full size image

2.2 Metallographic characterization

Macroscopic overview cross sections were prepared and the microstructure was investigated on micro sections, Fig. 5. The micro sections were etched with Nital. The weld metal microstructure of all four specimens was comparable and mainly composed of upper and lower bainite. A detailed analysis of this feed material and its mechanical parameters can be found elsewhere [35].

Fig. 5
figure 5

Macro- and micro-sections of specimens 1 to 4 build in vertical (left) and horizontal (right) position

Full size image

The hardness of all four specimens were comparable due to similar heat input and constant interpass temperatures, Fig. 6. This was important to isolate the effect of the surface from microstructural effects on fatigue properties. The hardness of all four specimens was analyzed by Vickers testing along the building direction. Additionally, a hardness mapping by means of the ultrasonic contact impedance (UCI) method was conducted in the vicinity of a layer boundary. The measurement results are shown in Fig. 6. The mean hardness of approximately 300 HV1 and corresponding interquartile ranges (IQR) were comparable for all four specimens. Overall, the hardness ranged from 280 to 325 HV1. The detailed analysis of the hardness near a boundary layer revealed slight softening near fusion lines, which was explained by annealing effects of subsequently deposited layers. The difference of hardness between layer bulk material and softened fusion line was approximately 340 HV0.1 – 270 HV0.1 = 70 HV0.1. The geometric notch at the surface coincidences with the softened layer boundary.

Fig. 6
figure 6

Results from hardness measurement HV1 along the building direction (left); Magnification of hardness distribution HV0.1 in layer structure of specimen 4 manufactured horizontally (right). Locations of measurements depicted in Fig. 5

Full size image

2.3 Surface evaluation

Surface waviness parameters were determined from the waviness profile according to ISO 4287 [36] and Eq. 2. The determination of the waviness profile from the measured profile was conducted in agreement with the procedure described in [31]. The cut-off wave length for the separation of the roughness was chosen in dependence of nominal layer height of the DED-arc process and was λc = 0.95 mm. The arithmetic mean deviation Wa was determined:

$${W}_{a}= \frac{1}{{l}_{n}}{\int }_{0}^{{l}_{n}}\left|Z(x)\right|dx$$
(2)

From all measurements, mean values for Wa and the corresponding standard deviations s were determined, Table 4. These parameters demonstrate the effect of the manufacturing position on the waviness. While the waviness on both sides of the specimens 1 and 2 is comparable, the bottom sides of specimens 3 and 4 showed higher values in comparison to the top side. This effect was explained by the acting gravity on the molten bead.

Table 4 Waviness parameters Wa and their standard deviation s of DED-arc specimens manufactured in different positions (vertical/0° and horizontal/75°)
Full size table

2.4 Estimation of effective wall thickness b eff

The effective wall thickness was evaluated by two methods. Method 1 estimated the effective wall thickness from the material volume deposited and surface waviness parameters, while Method 2 based on measurements of the wall thickness variation in metallographic macrosections.

In a first step, the theoretically resulting nominal wall thickness bn was determined from the volumetric flow rate of the feed material. The wire feed was measured (type HKS weld scanner) during DED-arc manufacturing of the four specimens. In combination with wire cross section (∅ 1.2 mm) and the preset process travel speed, the material flow was calculated. Assuming a rectangular layer cross section and on basis of the resulting layer height, a specimen-specific theoretic wall thickness could by estimated. The waviness parameters were used to estimate the wall thickness reduction. For this, a 95% quantile was determined from the mean value \(\overline{{W }_{a}}\) and the standard deviation s, assuming a normal distribution of Wa. The waviness on both sides of the specimens was considered:

$${W}_{a,95\mathrm{\%}}= \overline{{W }_{a}}+2s$$
(3)
$${{b}_{eff,M1}={b}_{n}- W}_{a,95\mathrm{\%}, side1}-{W}_{a,95\mathrm{\%}, side2}$$
(4)

The second approach applied, Method 2, evaluated the effective wall thickness from 2D macroscopic cross sections. For this purpose, the images of the cross sections of the four samples were converted into grayscale images and evaluated with respect to their contours using the Python library skimage. Figure 7 visualizes the methodology behind digital image measurement. A gray-scale image served as the input signal for image processing, filtering and automated contour detection based on defined gray-scale values (a). After contour detection, the wall width was measured by vertical profile cuts at intervals of 5 pixels (approx. 86 µm) and the conversion from pixels to millimeters was carried out. The wall width was determined at approximately 500 equally distributed positions in the blue highlighted wall area on all four specimens (b).

Fig. 7
figure 7

Algorithmic determination of the effective wall width based on cross-sectional images using specimen V1, grayscale image of the cross section (a), contour detection based on gray values using the Python library skimage (b)

Full size image

Figure 8 depicts the results of digital wall thickness measurement using automatic contour detection performed on specimens built in vertical and horizontal position. In addition, the diagrams show the statistical parameters mean wall width \(\overline{\mathrm{b} }\) and standard deviation s of the individual experiments. First of all, it is noticeable that the specimens with the same building positions 1 and 2 respectively 3 and 4 provided comparable results within the standard deviation, which testifies a high repeatability of the experiments. In addition, a significant influence of the building position on the wall thickness of the specimens is shown. With an average wall thickness of approx. 4.86 mm, the walls produced in a 75° building position are almost 0.74 mm thinner than the reference specimens produced at 0°. In the case of the vertically produced 0° specimens, the molten pool solidified over a larger area on the upper edge of the wall and consequently formed a significantly wider weld seam without the influence of gravity. Assuming a normal distribution, the effective wall thickness beff,M2 was estimated by:

Fig. 8
figure 8

Distribution of wall thickness measurement results of specimens 1 to 4 according to digital evaluation of wall cross sections based on approx. 500 individual measurements per specimen, vertical building position 0°, horizontal building position 75°

Full size image
$${b}_{eff,M2}=\overline{\mathrm{b} }-2s$$
(5)

2.5 Fatigue testing

Fatigue tests were conducted under sinusoidal constant amplitude loading at a stress ratio of R = (σu / σo) = 0.1. The dog bone fatigue test coupons extracted from additively manufactured specimens were extended in length with help of conventional sheet material S690Q. This was conducted to ensure safe grip in the hydraulic clamping of the test rig (type walter + bai, 250 kN). In total, approximately 15…16 layers were located in the reduced section of the specimen, which had width of w = 13 mm. The tests were conducted force-controlled until specimen rupture. All specimens failed in the area of the reduced section with cracks initiating from layer boundaries at the surface, Fig. 9. No internal defects were detected on fracture surfaces.

Fig. 9
figure 9

Geometry of the fatigue test specimens (top), failure example (bottom), and fracture surface with crack initiation (black box)

Full size image

2.6 Fatigue strength evaluation by effective notch stress approach

For the evaluation of the fatigue test results by the nominal stress approach, the effective wall thickness of fatigue test coupons needed to be evaluated (the “Wall thickness evaluation” section). Furthermore, the linear elastic effective notch stress approach was applied for the assessment of different surfaces resulting from variation of building positions. The finite element model was set up as a 2D model using elements with second order form functions. In regions with high stress gradients, the element edge length was 0.2 to 0.25 mm which was identified to result in less than 1% difference compared to a mesh with half the element size. A plane strain state has been assumed, since the middle of the specimens is investigated. The modulus of elasticity was E = 210 GPa and the Poisson’s ratio is ν = 0.3.

The geometric basis for the modeling were the aforementioned line scans of top and bottom surface of the specimens. 48 scans were analyzed on a per-specimen basis. For every fatigue testing specimen, the line scans in the middle were used to setup a model, Fig. 10. Within preliminary investigations, it was found that any scanned line can reasonably assumed to be representative, because of the significant statistical nature of failure in DED-arc structures and the large length of individual scans. Top and bottom scans were leveled by running a linear regression and subtracting the resulting linear graph from the raw data. The scan-data was smoothed by averaging the height of three neighboring data points to minimize effects of noise in the data. An offset distance of both scans had to be chosen, which was set to 6 mm for all specimens for simplicity reasons. The effect of a differing average thickness was compensated by consideration of the theoretical specimen width b in the final calculations (compare Table 5). The left edge was fixed while the right edge was loaded with 6 N tensile force and fixed perpendicular to the loading direction. This resulted in a nominal stress of 1 MPa.

Fig. 10
figure 10

Finite element model of specimen built in horizontal position (75°) with refined mesh near the surface (top) and magnification of a highly stressed region (bottom)

Full size image
Table 5 Waviness parameters Wa and their standard deviation s of DED-arc specimens manufactured in different positions (vertical/0° and horizontal/75°)
Full size table

The maximum principal stress was used for evaluation of the notch effects with the stress averaging approach. The stress averaging path was placed at the global maximum of the maximum principal stress, perpendicular to the surface, Fig. 10. Here, the commonly accepted averaging length ρ* = 0.4 mm was used and stresses were numerically integrated, as explained in the “Fatigue of weld metal and metallic AM components” section. The effective stress value σeff was then divided by the nominal stress. In consequence, the effective notch factor keff was obtained.

$$k_{\mathrm{eff}}=\frac1{\sigma_{nom}}\ast\frac1{\rho^\ast}\int_0^{\rho^\ast}\sigma\left(x\right)dx$$
(6)

3 Results

Two main effects of the surface waviness needed to be evaluated. The first effect of an inhomogeneous surface topography is the resulting wall thickness. In general, increased waviness results in lower effective load bearing wall thickness [37]. The effective wall thickness evaluation is described in the “Wall thickness evaluation” section with the goal to evaluate fatigue strength in the nominal stress approach. In addition, the notch effect of the surface topography was to be considered in a more generalized method. This was assessed by help of finite element modeling and application of the stress averaging approach (the “Resulting effective notch stress factors keff” section).

3.1 Wall thickness evaluation

Results of the estimated effective wall thickness (Method 1 and Method 2) are provided in Table 5. It varies between 5.38 and 4.09 mm depending on the manufacturing position and evaluation method.

3.2 Resulting effective notch stress factors k eff

For the evaluation of the notch effect of the surface topography, effective notch stress factors keff were determined. The values for every fatigue test coupon and the average values for specimen 1 to 4 are displayed in Table 6. For all series, an average effective notch factor of at least 1.5 was observed. The locations of the global maxima were distributed evenly between top and bottom side in the vertically built specimen. In the specimens welded at 75° overhang the notch factors on the rougher bottom side are significantly higher with an average > 2.4.

Table 6 Effective notch factors keff of specimens and averaged by wall number
Full size table

3.3 Fatigue test results

The fatigue test results of specimens manufactured in vertical and horizontal position are shown in Fig. 11. The series manufactured horizontally resulted in considerably lower numbers of load cycles until specimen rupture when comparing with vertically manufactured specimens. This difference was caused by the surface topography, which reduced the load-bearing cross section when the waviness increased and caused higher local stress concentrations.

Fig. 11
figure 11

Fatigue test results, test force amplitude, and load cylces until specimen rupture

Full size image

A nominal S–N diagram was determined on basis of the effective wall thickness beff estimated from Method 1 and Method 2, Fig. 12. A nominal stress range \(\Delta \sigma =\left(\Delta F/\left({A}_{\mathrm{eff}}\right)=\left(\Delta F/\left({b}_{\mathrm{eff}}\bullet w\right)\right)\right.\) was calculated and a mean stress correction factor of 1.16 (R = 0.5) was applied with reference to [38]. The S–N curves of specimens manufactured in vertical position still showed higher fatigue strength compared to horizontal position. The estimated effective wall thickness from Method 1 and Method 2 for vertically manufactured specimens was similar. In case of horizontally manufactured specimens, Method 2 resulted in significantly smaller values beff,M2 compared to Method 1. As a result, the difference of the two S–N curves from specimens manufactured in different building positions was larger when applying Method 1. In terms of design S–N curves, FAT 160 (vertical manufacturing position) could fit the data of vertically manufactured specimens well. The fatigue strength of horizontally manufactured specimens could be estimated by FAT 112 (Method 1) and FAT 125 (Method 2) respectively.

Fig. 12
figure 12

Fatigue test results, nominal stress amplitudes and load cylces until specimen rupture. beff from Method 1 (top) and Method 2 (bottom)

Full size image

The test results were further evaluated by application of effective notch stress factors σa,eff = keff x (Fa / beff), Fig. 13. A mean stress correction to an R-ratio of 0.5 was applied here as well. Interestingly, both test series could be evaluated by a single S–N curve. A k-value of 4.2 ± 0.6 was found to representative for the data set, resulting in a fatigue strength of approximately 230 MPa at 2 million load cycles. The data could be assessed by FAT 160 conservatively, when a k-value of 4 was applied.

Fig. 13
figure 13

Fatigue test results, effective stress amplitudes, and load cylces until specimen rupture

Full size image

4 Discussion

A more common use of AM technology is to be expected for structural metallic components. The DED-arc process holds high potential, especially for larger components where high building rates are needed. The surfaces of such parts are relatively rough with height differences in the mm-range. This is further enhanced by unfavorable building positions, where gravity acts perpendicular to the building direction. It was shown that the waviness parameter Wa varies from approximately 0.1 mm to 0.25 mm when changing the building position from vertical to horizontal. The thermal cycle caused a softening in the vicinity of the layer boundaries. A minimum hardness of approximately 270 HV1 was proven in these zones. The softening resulted in a tensile strength of 890 MPa of milled specimens, which corresponds well with the minimum hardness (ISO 18265: 270 HV ≙ Rm = 865 MPa). Additionally, the fatigue strength was significantly reduced by the notch effect. In the nominal stress approach, a reduction from FAT 160 to FAT 112 could be estimated. Fatigue cracks originated from layer boundaries with high stress concentration and softened material.

For future applications of the DED-arc process, we expect a large variety of alterative process designs and varying feed material. This will result in variations of surface topography, material resistance, geometric and metallurgical irregularities. A more general design approach should consider these parameters and resulting effects. Here, the effective notch stress approach was applied successfully to evaluate the surface effect on the resulting fatigue strength. However, more detailed information on material influence and process irregularities need to be gathered.

5 Summary and Conclusions

The influence of surface topography on load-bearing wall thickness and geometric notch effects needs to be understood to enable the use of the DED processes also for structural components. Specimens were manufactured by means of the DED-arc process from high strength feed material. The process parameters were kept constant while the building position was varied, which resulted in comparable material properties. As a result of varying building positions, the gravity acted differently on the solidifying melt bead and varying surfaces were generated. Fatigue tests were performed and evaluated. The main findings of the conducted investigations are:

  • • The surface waviness increased significantly when working in horizontal position

  • • The tensile strength was limited by softened zones in the vicinity of layer boundaries

  • • The effective wall thickness on unmilled test coupons correlated with the waviness parameter Wa

  • • The surface effect became visible in the nominal stress approach. For statistically relevant correlations more data is needed

  • • The effective notch stress approach was applied successfully. A S-N curve exponent value of k = 4 was applied successfully and fitted the data well