1 Introduction

The effective notch stress approach, as described in the IIW recommendations [1] and related literature, see e.g. [2,3,4], can be used for the analytical determination of fatigue strength of welded components. As a requirement, the stress concentration factor either referring to maximum principal stress or von Mises equivalent stress calculated using linear elastic mechanics has to be given.

By using a fictitious radius \(r\) when modelling the joints, the calculated stress concentration factor \({K}_{t}\) can be interpreted as an effective fatigue notch factor\({K}_{f}\). This effective notch stress concept, also proposed in the IIW recommendations [1] was developed by Seeger et al. [5] in the’80 s. The concept is based on the early works of Radaj [6] and Neuber [7]. With this unified approach for modelling and the incorporation of fatigue strength scattering by e.g. the influence of material data or geometrical details into the S–N curve a standardized model for analytical stress calculation was achieved. For more information also see our previous papers on cruciform and butt joints [8, 9].

With computational simulations, e.g., finite element analysis, these stress concentration factors can be easily obtained by creating a suitable model and performing numerical analysis and convergence studies. Many practitioners refuse this effort, especially when a multitude of welded joints must be evaluated, which often leads to the notch stress method being the second choice. Nevertheless, the method can cover, e.g., some size effects or different flank angles, which increases the applicability of this method compared to the nominal or structural stress concepts.

Therefore, different authors have developed empirical formulae by regression analysis of existing solutions as an alternative. These formulae were the only economical way to supply stress concentration factors. With increasing capabilities in finite element simulation, new and wide-ranging approaches become viable. Nevertheless, reliable empirical formulae can be worth thousands of simulations when providing results of high quality with respect to the exact or reference solutions. Their application can save a lot of time and computational effort.

Equations to support efficient estimations of stress concentration factors applying the effective notch stress approach have been derived by different authors for many decades already. Early notch factor determination methods were either based on experimental data or on photoelastic methods [2]. Procedures that are more recent are mainly based on numerical finite element simulation but also these procedures lack precision because of limited computing capacity at the end of the last decade. To mention are the methods by Yung and Lawrence et al. [10, 11], Brennan [12], Iida and Ushirokawa [13], Tsuji [13], Rainer [14], and Hellier [15].

To address the inherent problems of the existing methods, two new methods, based on excessive numerical simulations and metamodeling are proposed. Firstly, the PRC method by polynomial regression with coupling terms, and secondly, the ANN method by applying artificial neural networks.

2 Numerical simulation of welded T-joints

Welded T-joints were considered in this study. The sheets are welded by fillet welds on both sides of the connecting sheet, both with full and partial penetration. No axial or angular misalignment of the sheets is considered. If misalignment is present in the structure, it must be contained in the stress analysis as a secondary effect or by reducing allowable stresses.

2.1 Parametrization

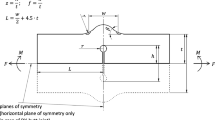
Finite element models with parametric geometry were modeled using ANSYS Mechanical™ 20 R1Footnote 1 (see Fig. 1 and Table 1) [8]. These numerical models enable the assessment of stress concentration factors at the weld toes and the weld roots using linear-elastic finite element analysis. The parametric models were loaded under tension, see Fig. 2. Full as well as partial penetration welds are considered.

Fig. 1
figure 1

Parametrized geometry of the T-joint with full and partial penetration

Full size image
Table 1 Parameter ranges of numerical model
Full size table
Fig. 2
figure 2

Load scenario

Full size image

The following assumptions are used:

  • No axial or angular misalignment

  • No nonlinear contact in the non-fused root face

  • Equal reference radii of weld toe and weld root, modelled as fillet radii

  • The weld reinforcement is modelled by a straight line

  • Plane strain condition

  • Constant parameters for linear elastic material:

    • Young’s modulus \(E=210GPa\)  

    • Poisson ratio \(\nu =0.3\)

  • Uniform tension nominal stress of \({S}_{t}=1MPa\)

  • Evaluation of maximum principal stress \({\sigma }_{1}\)

In addition to using principal stresses an evaluation of v. Mises equivalent stress could be performed; however, the given FAT classes by DVS-Merkblatt 0905 [3] are valid for principal stress. The effective notch stress approach requires a reference radius depending on the sheet thicknesses \(t\). For this model extended recommendations for the radius selection according to DVS-Merkblatt 0905 [3] have been used. Those recommendations represent an extension to the IIW recommendations for thin- and thick-walled welded structures [1]. The range of the sheet thickness was divided into three overlapping sub-ranges where an adequate reference radius can be assigned (see Table 2). The ranges according to Table 2 exceed the allowable values for almost all the existing empirical rules to calculate the notch stresses. It was the main goal of this study to increase the design space of new empirical rules towards more general applicability and versatility.

Table 2 Parameter Ranges for Space Filling Latin Hypercube Samplings
Full size table

2.2 Finite element modelling

To analyze the notch stresses correctly the generally coarse global mesh is refined at the weld toe and the weld root. A preliminary convergence study showed converged notch stresses using a mapped mesh of quadratic PLANE183 elements with element lengths of \(0.05\cdot \rho\) in the notch up to a depth of \(0.4\cdot \rho\).

A 2D-modeling approach with plane strain condition was used for finite element calculation of the first principal stresses in the weld toe and root. Nevertheless, the differences between the plane strain and plane stress conditions in the simulation must be considered. A minimum total depth of the sample must be met to establish a plane strain condition in the middle of the sample.

The system for each type of T-joint was split into six subsystems in dependency on wall thicknesses and their corresponding reference radii as well as existent or non-existent non-fused weld root faces (see Table 2). The corresponding wall thickness ranges have been chosen so that they overlap each other for different notch radii. In overlapping ranges of thickness, a reasonable notch radius has to be chosen in order to meet the requirements given in DVS-Merkblatt 0905. For each subsystem, a Space Filling Latin Hypercube Sampling was created with optiSLang® 6.1.0.Footnote 2 For each subsystem in Table 2, approximately 1000 samples have been produced and calculated using linear elastic FEA.

Further information on sampling and modelling can be found in [8, 9].

3 Known methods of notch factor estimation of T- joints

There are several methods for the determination of stress concentration factors at welded T-joints. However, most of them are primarily intended for transverse stiffeners, so that they cannot be applied for the load case presented here. Only the methods according to Yung and Lawrence [10, 11] as well as Iida and Ushirokawa [13] offer an approximation method here. These are presented in this section. All the following equations as well as the new methods in the following chapters of this paper are based on maximum principal stress \({\sigma }_{1}\).

3.1 Method by Yung and Lawrence

Based on Lawrence’s procedure [10] based on finite element simulations, Yung and Lawrence described a refined method in 1985, including a variety of data from other publications [11]. Their approximation formulae are valid for all investigated T-joints (with and without non-fused root face under tension loading) limited by the flank angle of \(\alpha =135^\circ\).

Yung and Lawrence are using the sheet thickness \({t}_{\mathrm{1,2}}\), notch radius \(\rho\) and the length of the non-fused root face \({l}_{NF}\) for their approximation formulae given in Table 3.

Table 3 Method by Yung and Lawrence
Full size table

3.2 Method by Iida and Ushirokawa

Iida [13] also proposes a method based on an investigation by Ushirokawa. Their formula is restricted to \(110^\circ <\alpha <140^\circ\), \({t}_{1}=20mm\), \(0.5mm<\rho <7mm\), \(6.43<{t}_{1}{f}_{a}<18.79\) and \(5mm<{t}_{2}<20mm\) as well as only tension loading for T-joints. The formula is given in Table 4. Their formula is therefore only usable for the tension load case 1 and a radius of \(\rho =1mm\).

Table 4 Method by Iida and Ushirokawa
Full size table

4 New methods of notch factor determination

Metamodeling is an umbrella term for modern regression methods. Those polynomial regressions involving coupling terms to generate response surfaces and neural networks have been selected for this study, since recent investigations on the determination of notch factors for welded cruciform joints [8] and butt joints [9] have proven the adaptability of these two regression methods. The results are presented in the following.

4.1 Polynomial regression with coupling terms (PRC method)

In optiSLang® 7.2.0 polynomial regression functions with quadratic order and coupling terms are fitted using the numerically calculated stress concentration factors from finite element analysis. The calculation is carried out according to Eq. 3. The factors according to Tables 11 and 12 of the Appendix can be chosen according to Table 6.

$${K}_{t,PRC}=\sum_{k=1}^{15}{c}_{k}\bullet {f}_{k}({t}_{1},{t}_{2},\alpha ,{f}_{a},{f}_{NF})$$
(3)

Since five parameters \(({t}_{1},{t}_{2},\alpha ,{f}_{a},{f}_{NF})\), their squares, each combination of two parameters and an additional fixed term are used, and the total number of 35 terms is used in the regression formulas. In order to simplify the regression model, an automatic variable reduction is done during regression. Only variables that meet the conditions of the significance and importance filter are considered in the regression function [16]. The standard filter setting of optiSLang is used. Therefore, easier applicability while maintaining almost the same predictive quality is achieved. This procedure results in up to 10 parameters in the formulae for T-joints without non-fused root face and 15 parameters in the formulae with non-fused root face. In total, 9 regression formulas for the T-joint have been developed, one for each combination of reference radius and joints with and without non-fused root face, see Table 6.

Also, the PRC method must be restricted to certain geometry parameters according to the simulated parameter combinations which were used for regression, see Table 5. Table 6 shows the nomenclature for the stress concentration factors of the PRC method.

Table 5 Restrictions of the PRC method
Full size table
Table 6 Stress concentration factor for maximum principal stress formulae according to the new method
Full size table

4.2 Application of artificial neural networks (ANN method)

Data fitting of the calculated finite element results was done with Matlab’s Neural Network Toolbox. The classical feed-forward neural network used consists of three hidden layers. Each hidden layer consists of four or four or five neurons in accordance with the number of input variables \(({t}_{1}, {t}_{2},\alpha ,{f}_{a},{f}_{NF})\). The output layer consists of one neuron for the stress concentration factor as the output variable \(\left({\mathbf{k}}_{t}=\left({K}_{t,ANN}\right)\right)\), see Fig. 3. The database has been split into 70% training and 30% test and validation data.

Fig. 3
figure 3

Schematic structure of the artificial network

Full size image

After normalization of the input variables to avoid overestimation or underestimation of the input’s influence, each layer multiplies its inputs with a weight matrix \({\mathbf{W}}_{i}\) and shifts it by a bias \({\mathbf{b}}_{i}\), which results in the layer potential \({{\boldsymbol{\upphi}}}_{i}\). The potential is then put into a hyperbolic tangent sigmoid transfer function in the case of the three hidden layers or a linear transfer function in the case of the output layer, which finally gives a vector of outputs in terms of stress concentration factors after renormalization.

Restrictions in terms of parameter ranges according to Table 5 must be given, defined by the parameter ranges of the training data, like the PRC method.

For more information on the mathematics of neural networks, see for example Hagan et al. [17]. The multilayer approach with a low number of neurons in each hidden layer resulted in a better estimation of stress concentration factors than a single-layer approach with a high number of neurons in the layer. Additionally, benefits in training and evaluation time could be accomplished.

The mathematical expressions for the used network can be found in Table 7, the corresponding normalization vectors, weighting matrices, and bias vectors can be found in Tables 13, 14, 15, 16, 17, 18, 19, 20 and 21.

Table 7 Formulae of the ANN method
Full size table

5 Comparison of notch factor determination and quality

All existing and new methods have been applied to the data taken from the finite element simulation and compared with its results. Keep in mind that limitations to the methods were given:

  • All authors give limitations to their methods, summarized in Table 8. Some of them are significantly restricting the allowable design space compared to the new approaches as presented in this paper.

  • Stress concentration factors below unity were neglected. Please be advised that the ratio of notch stress to structural stress \({K}_{w}={\sigma }_{e}/{\sigma }_{w}\) has to meet a lower limit \({K}_{w,min}\) for the corresponding stress concentration factor to be permissible for use in the notch stress concept, see Rother and Fricke [18]:

    $$\begin{aligned}&K_{w,min}=1.6\;\mathrm{for}\;\rho=1mm \\ & K_{w,min}=2.13\;\mathrm{for}\;\rho = 0.3mm\\ & K_{w,min}=3.56\;\mathrm{for}\;\rho =0.05mm\end{aligned} $$

    Nevertheless, samples not exceeding these ratios were used in regression as well, since these ratios always must be checked by the user himself, depending on parameter combination and loading.

    In previous investigations of welded cruciform joints [8, 9], it was found that the quadratic extrapolation method leads to the lowest structural stresses and therefore to the most non-conservative results for \({K}_{w,min}\).

Table 8 Overview of all restrictions given by the authors, T-joint
Full size table

Due to the given limitations, most of the results (see Table 9) from finite element calculation must be neglected.

Table 9 Statistical data of all evaluated parameter combinations, sorted by evaluation method, quantiles counted and % of samples used for the respective method, at weld toe
Full size table

5.1 Comparison of methods for T-joints

All the following figures show the resulting relative errors for all investigated methods as boxplots on the left side. The red line in the central blue boxes indicates the median relative error which should ideally be zero. The blue box around it shows 50% of the data points with their upper and lower boundary indicating the \(25\%\)- and \(75\%\)-quantiles. The black lines, so-called whiskers, embed \(1.5\) times the interquartile range from the \(25\%\) to the 75%-quartile of the data. This corresponds to about 95.4% of all data for normal distributions. Finally, the red crossed data outside of the whiskers indicate data points being lower than this range. On the right side, both figures show probability plots of each method for normally distributed data. Perfect normal distributed data would adapt to the linear regression line.

Figures 4, 5, and 6 show boxplots and probability plots generated with data fulfilling the restrictions the authors have given individually for each method for T-joints. Figures 4, 5, and 6 show the data for T-joints under tension.

Fig. 4
figure 4

Boxplot and probability plot of the relative errors for normal distribution—T-joint, tension, without non-fused root face at weld toe

Full size image
Fig. 5
figure 5

Boxplot and probability plot of the relative errors for normal distribution—T-joint, tension, with non-fused root face at weld toe

Full size image
Fig. 6
figure 6

Boxplot and probability plot of the relative errors for normal distribution—T-joint, tension with non-fused root face at weld root

Full size image

For the following, the relative error is calculated by

$$er{r}_{rel}=\frac{{K}_{t,EST}-{K}_{t,FEM}}{{K}_{t,FEM}}[\%]$$
(9)

Table 10 shows the percentage of data that had to be neglected in comparison to the total data available for evaluation by the restrictions given by the authors. Remarkable are the low error values and a high number of evaluable results for the PRC and especially the ANN methods that demonstrate the much larger range of application of those metamodels.

Table 10 Statistical data of all evaluated parameter combinations, sorted by evaluation method, quantiles counted and % of samples used for the respective method, at weld root
Full size table

Looking at Figs. 4, 5, and 6, the new metamodels based on polynomial regression with coupling terms and artificial neural networks cluster the results around a mean relative error of 0% compared to the results given by Finite Element Simulation. The existing methods by Yung and Lawrence as well as Iida and Ushirokowa are shifted to the unsafe side and underestimate the stress concentration factors.

In terms of scattering, the new ANN method shows the lowest scattering comparing \(25\%\)- and \(75\%\)-quantiles. The PRC method is quite comparable to the existing methods by Yung and Lawrence and Iida and Ushirokawa. Note that the new PRC method is by far less restrictive in terms of applicability. Comparing the \(1\%\)- and \(99\%\)-quantiles, the ANN method shows the lowest scattering for both penetration types, followed by the PRC method and the existing methods.

6 Conclusion

To investigate the quality of selected existing analytical estimation methods for stress concentration factors for welded T-joints with and without non-fused root face under tension loading numerical simulations using many samples and a broad range of parameter variations were conducted. The resulting stress concentration factors with respect to maximum principal notch stress at plane strain conditions were used as reference solutions for comparison of the estimated factors.

Selected methods for the estimation of stress concentration factors by empirical formulae have been investigated and presented in summary also considering their respective ranges for application as given by the authors for the geometrical parameters. Additionally, two new methods for metamodeling were introduced and suggested for future use: one analytical method based on polynomial regression involving mixed terms and one method using artificial neural networks. In both cases, the ranges of application cover a significantly improved versatility by allowing very large ranges of the different parameters involved. Using the two proposed methods, thin-, medium-, and thick-walled welded T-joints are covered as well as three different notch radii and a varying flank angle and weld seam width. Both methods yield stress concentration factors of similar quality and low scatter with respect to error from numerical reference values.

It can clearly be shown that using the new methods can give – significant improvement in both the mean estimation of stress concentration factors as well as on reducing the scatter in estimated results by simultaneously significantly increasing the range of applicability compared to existing approximate methods. The methods suggested in this paper provide a reliable basis for an efficient, fast, and reliable estimation of assessing relevant stress concentration factors for different notch radii used in the effective notch stress concept according to IIW and related guidelines. Thus, the time-consuming creation and analysis of numerical models can be avoided without a significant lack of accuracy. The new methods presented might also be included in higher-level applications for the design and efficient optimization of welded structures involving T-joints. The stress concentration factors obtained by the new methods are valid for plane strain conditions and maximum principal stress.

The new methods using PCR and ANN will be programmed and made available besides other existing predictors for welded joints to the community by http://rother.userweb.mwn.de/scf-predictor.html. With this application user friendly and quick computations of stress concentration factors using Eqs. 3 to 8 can be performed.