1 Introduction

The fatigue strength of welds is generally lower than that of the base material. This is due to different reasons: First, the local weld geometry has a detrimental influence due to the induction of macroscopic notches [1]. The notches are located in the weld toe and their geometry is characterised by the local flank angle \(\theta\) and the local notch radius \(r\) or other parameters like the undercut or notch depth t′. At these notches, external load stresses are concentrated. This stress concentration can cause high plastic strains leading to an earlier crack initiation compared to pure base material [2]. Depending on the welding process, detrimental residual stress states as well as variations in hardness and microstructure across the weld can be induced [3]. The variations in hardness and microstructure occur due to the phase transformations resulting from the heat input. Detrimental residual stresses are mostly created by possible hindered shrinkage of the weld surrounding material during the cool down phase of the newly generated welded joint. In the past, post-weld treatment methods such as burr grinding, tungsten inert gas welding, shot peening, or high-frequency mechanical impact treatment have been extensively investigated [4, 5]. All these methods aim to either induce beneficial subsurface properties such as compressive residual stresses as well as strain hardening or to influence the local weld geometry regarding a reduction of stress concentration. A promising method to enhance the fatigue strength of welds is the deep rolling process. The influence of deep rolling on the local weld toe geometry has not been quantified yet. In this study, an innovative approach regarding the automated measurement and evaluation of the local weld toe geometry before and after deep rolling using a conventional machine tool is presented. Furthermore, first results regarding the influence of mechanical load caused by deep rolling on the local weld geometry are evaluated.

1.1 Deep rolling of welds

In mechanical engineering, deep rolling is often used to enhance the fatigue strength of metallic components like crankshafts, turbine blades, or wheel flanges. This is due to the positive influence of the deep rolling process on the surface and subsurface properties of the component [6]. In deep rolling, a carbide or ceramic ball is pressed against the surface of the component by means of hydrostatic pressure and moved along using a conventional machine tool or robot. In the case of deep rolling, the parameters rolling pressure pr, overlap factor u, line spacing ab and ball diameter db have a decisive influence on the resulting surface and subsurface properties [7]. Common ball diameters are db = 3.175–12.7 mm and common rolling pressures are pr = 10–60 MPa, which are provided by a hydraulic unit. The resulting rolling force Fr can be calculated according to Eq. (1). The pressure medium often used is standard machine cooling lubricant emulsion.

$$F_r=\pi\cdot\left(\frac{d_b}2\right)^2\cdot p_r$$
(1)

The deep rolling process changes the surface and subsurface due to elastoplastic deformations and possible phase transformations that occur during the mechanical contact [8]. The penetration of the rolling body into the workpiece causes plastic strains in radial direction. These plastic strains are compensated by elastic compression of surrounding material in order to maintain the volume constancy of the body. The result are compressive residual stresses. Furthermore, elastoplastic deformation can lead to strain hardening: Forming dislocations hinder each other and make further deformation more difficult. The hardness of the material has an influence on the development of compressive residual stresses. In the case of unalloyed steels in normalised state, the compressive residual stress maximum is formed directly on the surface. In the case of hardened and tempered steels, it is located below the surface [9]. The different formations of the compressive residual stress maxima are due to the material behaviour under contact load. In soft materials with a Vickers hardness (HV) below approx. 300 HV, the plastic elongation or stretching of the surface dominates; in hard materials with a Vickers hardness above approx. 600 HV, the Hertzian compression is dominant. Mixed formations of the contact behaviour might occur for materials of Vickers hardness between 300 and 600 HV [10, 11].

The Hertzian contact mechanic relations assume frictionless, smooth surfaces and purely elastic material behaviour with small strains. Nevertheless, the formulas are widely used to describe the rolling contact for a wide variety of material states and process kinematics [12]. With the help of the Hertzian formulas, the forming contact radius rc between a sphere and a flat surface due to indentation of the ball into the surface can be calculated according to Eq. (2), resulting in an analytical description of the overlap factor u (3), see Fig. 1.

Fig. 1
figure 1

Explanation of the deep rolling overlap factor u

Full size image

Therefore, knowledge about the modified Young’s modulus E’, which depends on the material pairing of contact partners, and Poisson’s ratio v of the workpiece is necessary [12].

$$r_c=\sqrt<span class='reftype'>[3]</span>{\frac{3\cdot\left(1-v^2\right)\cdot d_b\cdot F_r}{4\cdot E\;^\prime}}$$
(2)
$$u=1-\frac{{a}_{b}}{2\cdot {r}_{c}}$$
(3)

The deep rolling process and its influence on the surface and subsurface properties of welds was investigated sparsely in the past. Farajian et al. investigated the influence of deep rolling on the surface roughness and the surface near residual stress state of tubular tungsten inert gas welded construction steel S690QL (1.8928) [13]. They were, for example, able to achieve a reduction of the surface roughness parameter Rz from initial Rz = 4.58 µm to Rz = 0.87 µm or of the surface roughness parameter Rmax from initial Rmax = 5.38 µm to Rmax = 1.19 µm. Furthermore, they found, depending on the initial residual stress state of the weld, compressive residual stresses as high as the ultimate tensile strength of the S690QL base material in axial direction of the tubular welded joint (\({\sigma }_{r} \, \text{=} \, \text{- }\text{1050 MPa}\)).

Additionally, Schubnell et al. [14] investigated the influence of deep rolling on surface and subsurface properties and the fatigue resistance of orbitally metal active gas welded construction steels S355J2 (1.0577) and S690QL (1.8928) and tungsten inert gas welded aluminium EN AW 5083 (3.3547). For both construction steels and the aluminium, slight increases in hardness depth profiles compared to the as welded condition were found. The authors also investigated the surface near residual stress state after deep rolling. For each of the examined materials, a pronounced compressive residual stress state was found. For S355J2, the compressive residual stresses, measured by X-ray diffraction, were even higher than the ultimate tensile strength of the material (\({\sigma }_{r} \, \text{=} \, \text{- }\text{650 MPa}\)). After deep rolling, the authors conducted rotating bending fatigue tests with the tubular specimens. A significant increase in fatigue strength compared to the as-welded condition was found for each examined material: 47% increase for S355J2, 92% increase for S690QL and 48% increase for EN AW 5083. For comparison reasons, in another test series, Schubnell et al. fatigue tested shot-peened specimens of the same aluminium material. Although higher roughnesses and lower compressive residual stresses of shot-peened specimens were measured, the increase in fatigue strength compared to the deep-rolled specimens was another 25%. They clearly attribute that to the effectiveness of the deep rolling process in the vicinity of the weld toe, assuming that the small shots achieve a better treatment of the small notch compared to the relatively big deep rolling ball. An investigation of the influence of deep rolling on the local weld geometry was not conducted.

Coules et al. [15, 16] investigated the influences of a rolling process called high-pressure rolling on the subsurface properties of gas metal arc welded construction steel S355JR. This rolling process is different to the deep rolling process known in mechanical engineering. Here, a roller of dimensions d × t = 100 mm × 30 mm is rolled on the weld bead after the welding process in order to induce compressive residual stresses in the welded joint and achieve strain hardening of the weld. The process forces required for significantly influencing the subsurface properties of the welded joint reach up to \({\text{F}}_{\text{r}}\text{ = 150 kN}\). Although the high-pressure rolling did create relatively high amounts of compressive residual stresses and a relatively high degree of strain hardening in the weld bead, no significant increase of fatigue life in four-point bending fatigue tests could be observed [17]. The high-pressure rolling process did even lead to a reduction of the fatigue life. This is because during high-pressure rolling of the weld bead, the fatigue-critical location of the welded joint, which is the weld toe or the heat affected zone, was not influenced.

The fatigue resistance of welded joints is significantly influenced by the local weld subsurface properties and weld geometry. To enhance the fatigue strength of the welded joint using the deep rolling process, knowledge about the influence of the parameters of the deep rolling process on the local weld geometry is necessary.

1.2 Determination of the local weld toe parameters

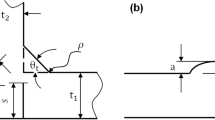
For fatigue-stressed welded joints, a large correlation between the local weld geometry and the fatigue life exists [18,19,20]. Various studies [2, 18, 19, 21,22,23] have shown that especially the notch radius and the flank angle have a significant influence on the local fatigue strength. Therefore, the weld geometry is usually quantified by these two parameters, see Fig. 2.

Fig. 2
figure 2

Definition of weld geometry parameters flank angle θ and notch radius \({\text{r}}\) of a butt welded joint

Full size image

In general, small notch radii and large flank angles have a stress-increasing effect [24]. To determine the local weld toe parameters various methods exist in the literature [1, 25,26,27,28]. In general, the determination of the weld toe parameters is based on two-dimensional geometry data sets perpendicular to the weld seam. However, no standardisation or recommendations are available for the determination of notch radius and flank angle. Also, the functionality of the existing methods differs greatly: Algorithms for fully automated or semi-automated determination of the parameters exist, but some methods are also based on manual analysis. In addition, the existing methods are not always suitable for all types of welds [1].

In Schubnell et al. [1], a significant influence of the evaluation method on the determined notch radii is shown. Unfortunately, detailed information about the functionality of the existing methods is rarely available in the literature. The comparison of the methods but also of the results is therefore only possible to a limited extent. An algorithm used to determine the influence of deep rolling on the weld toe parameters is described in detail in this work. The method is fully automated and is universally applicable for different weld types.

1.3 Weld geometry measurement

For the analysis of weld seams and the evaluation of the usability of welded components, a lot of different inspection concepts have been industrially established. Preferably, non-destructive measuring methods are applied in order to avoid component damage. Therefore, the application of optical sensor techniques for geometric weld measurement and data processing are being investigated in research.

The industrial market disposes different measurement methods and systems, which strongly differ in precision, handling and applicability [29]. Harati et al. [30] investigated the usability of a laser line and a structured light system to measure the radius of the weld toe in corner fillet welds. Both systems were rated as suitable for this measurement task. Schubnell et al. [1] extended the investigations by comparing laser line and structured light sensors with different vertical accuracy and lateral resolution. The welded specimens were sprayed with contrast powder before scanning. Manufacturers of scanning sprays recommend a layer thickness between approx. 2–35 µm [31, 32], depending on medium composition and material to be scanned, which leads to an offset and deviation of the actual weld geometry. The data evaluation in Schubnell’s publication shows that the measured geometry value varies depending on the selected measuring system. Schork et al. [2] applied different measurement methods to investigate the weld geometry. The excess weld metal height h and the weld width L were measured with a laser sensor and for the secondary notch depths k optical 3D scans with a confocal microscope were used.

In the welding process monitoring and in the case of weld seam re-machining, like in aero engine and mould tool repair processes, the use of optical systems for geometry measurement is also investigated [33, 34]. In these applications, besides accuracy the focus is especially on fast, error-free geometry acquisition, data processing as well as integration in the manufacturing system. In welding process monitoring, optical systems for seam detection and following seam inspection are researched [34]. For weld seam re-machining, the so-called re-contouring, optical sensors are integrated into the processing machine or robot system [35]. Denkena et al. [36, 37] integrated a laser line sensor into a CNC machine tool to scan moulding tools and fan blades with repair welds to enable an optimal tool path planning.

2 Experimental setup

To quantify the influence of the deep rolling process on the local notch geometry, the experimental chain shown in Fig. 3 was conducted. The specimens were measured using an innovative automated scanning method in the initial state and in the deep rolled state. Afterwards, the extracted line scans were on the one hand used to evaluate the notch radius r and the flank angle θ for the initial and post-treated state. On the other hand, the line scans were integrated into a 2D-FE-Simulation to evaluate the local stress concentration for the initial and post-treated state.

Fig. 3
figure 3

Outline of conducted experiments

Full size image

2.1 Specimen preparation

The specimens investigated are submerged arc welded butt joints extracted from various large sheets (2200 mm × 600 mm × 19 mm) from the construction steel S355G10 + M Z35 (1.8813). The large sheets were welded automatically at the EEW GmbH & Co KG. The filler material used was EN ISO 14171-A: S2MoTiB [38]. The welds contain seven weld layers. After the welding process, remaining powder was removed and the large sheets were tested ultrasonically to ensure that there were no contaminants or internal defects in the joint. Afterwards, the specimens were extracted by waterjet cutting. The final contour of the specimens was generated by flank milling. For the geometry investigations using the line sensor the specimens were cleaned from remaining slag and oxide layers.

2.2 Automated scanning method

The state of research illustrates that detailed geometry data should be available for the evaluation and post-processing of weld seams. However, current measuring concepts have several deficiencies, especially in automation. Complex manual pre- and post-processing steps are required to achieve suitable results. These include the pre-treatment of the specimens with an anti-reflective spray, the application of reference points as well as the subsequent fitting, processing of blemishes and conversion of the point clouds.

This paper presents an innovative scanning method, which uses an optical laser line sensor, a CNC machine tool and a self-developed software system to determine the geometry data of welded specimens with high accuracy and automation. For the scanning system, an LJ-V7080 laser line sensor by Keyence Corp. is used. The laser sensor works according to the triangulation principle and consists mainly of semiconductor lasers, lenses, processors and a CMOS chip. The emitted laser beam by the sensor is expanded to a laser line on the target object. The resulting reflection on the target object is processed by the CMOS chip. With this measuring principle, height profiles can be determined fast and precisely in two dimensions. The LJ-V7080 structure and components as well as the specifications are briefly displayed in Fig. 4.

Fig. 4
figure 4

Structure and specification—Keyence LJ-V7080

Full size image

The measurement accuracy in the z-axis (height) of the LJ-V7080 laser line sensor is not specified by the manufacturer Keyence. However, this specification value is very crucial for the evaluation of the measuring task. Therefore, measuring experiments were carried out on a reference workpiece with defined different height levels. The level distances Δ z were first measured tactilely on a high-precision coordinate measuring machine Leitz Reference XI 10 ∙ 7 ∙ 6 / B5 (accuracy < 1 μm) in a measuring room and secondly scanned with the LJ-V7080 laser line sensor in the CNC machine tool. As a result, a mean measuring deviation in the z-axis of about 10 μm and a standard deviation of approx. 6 μm (in a range of ± 5 mm to the reference distance) were determined for the LJ-V7080 in reference to the tactile measurement method.

Figure 5 shows the measurement concept. By using a multi axis CNC machine tool, an optical laser line sensor and a self-developed scan software, the geometric properties of welded parts can be determined fully automated with high accuracy. The initial setup for the scanning process is a clamped welded specimen in the machine area. At the beginning of a new measuring task, a hybrid NC-code is generated with adaptive measuring path planning in order to combine the advantages of tactile and optical measurement systems. With a tactile 3D measurement system, vertically oriented surfaces can be determined with high accuracy.

Fig. 5
figure 5

Automatic weld seam scanning method

Full size image

The optical laser line measuring method is particularly suitable for fast and precise scanning of geometrically accessible component surfaces and welded seams. At the beginning of each series of measurements, a 3D touch probe is inserted into the machine tool and the position of the specimen in the machining area is determined. If it is necessary, the specimen position will be automatically corrected by the rotary axis of the machine rotary table. Afterwards, the workpiece zero point is set and the touch probe is exchanged (see Fig. 5).

In the second step, the weld geometry is scanned by a laser line sensor integrated in the machining area. During the scanning process, the data of the scan line and the axes positions are read out and linked together. The motion speed of the laser line sensor head in the CNC machine tool is limited according to the sampling rate (incl. new data values) of the machine axes (approx. 125 Hz, 8 ms, via Ethernet), of the sensor control unit (approx. 666 Hz, 1.5 ms, via USB) and the calculation speed of the software application (approx. 50 Hz, 20 ms, on Win 10). In order to generate a point cloud in a manageable and structured data format, the measuring points and axis data are queried by the scan software at defined intervals by a read-out timer algorithm. For this, the self-developed scan software is implemented on an industrial PC which is connected to the CNC machine tool control and scan control device. Any sensor settings and machine data can be retrieved and set (see Figs. 4 and 5).

Table 1 shows the sensor settings which are used for the geometric measurement described in this paper. The settings are well suited to scan the welded samples without a pre-treatment. A detailed description of the sensor settings is available in the LJ-V Series Setup Guide [39]. The scan process settings are listed in Table 2.

Table 1 Sensor settings
Full size table
Table 2 Scan process settings
Full size table

Figure 6 shows the scanning process in the CNC machine tool. The laser sensor is mounted on the spindle box and oriented to the machine axes. The specimen is fixed in a clamping vise on one side. The complete scanning process (front and back side) including 3D tactile referencing and clamping, reclamping and unclamping takes less than 5 min for each specimen.

Fig. 6
figure 6

Scanning process of the welded specimen

Full size image

To eliminate minor interfering reflections and signal noise which occur during the scanning process of an untreated weld sample, the measured points are optimised by an own filter algorithm. To reduce variations, each profile line is smoothed by a moving average with a width of 8 and is filtered afterwards with a median filter over 5 points. The final result of the introduced scanning process is an optimised point cloud of the weld seam. The point cloud can be used directly to analyse the geometric properties and be transmitted to the CAD module for a surface generation. Afterwards, an ideal tool path planning, e.g. for a deep rolling or milling process, can be designed via CAM software.

2.3 Deep rolling of welded specimens

The deep rolling process was conducted using a CNC-controlled milling centre. The experiments were performed using a HG3 tool with a ball diameter of db = 3.175 mm from the manufacturer ECOROLL AG Werkzeugtechnik. For the first experiments the pressure was held constant at pr = 30 MPa. The line spacing ab was chosen to achieve an overlap factor of u = 0.75. The deep rolled workpieces are specimens that were fatigue tested after the experiments. The specimen geometry and the experimental setup is depicted in Fig. 7.

Fig. 7
figure 7

Specimen geometry and experimental setup

Full size image

The direction of deep rolling was parallel to the direction of welding, starting at a distance of 5 mm from the weld toe. The chosen direction is due to the generation of higher compressive residual stresses transverse to the direction of deep rolling. Subsequently, the deep rolled specimens were measured using the optical laser line sensor, evaluated by an algorithm and afterwards numerically investigated.

2.4 Evaluation algorithm for the weld toe parameters

Based on the filtered profile, shown in Fig. 8, the local notch radii \(r\) and flank angles \(\theta\) were calculated using an algorithm implemented in MATLAB R2019a. The algorithm originates from Zein El Dine [40] and has been further developed in [41,42,43] for the respective use cases. For a fully automatic determination, the existing algorithm was modified and is described in the following.

Fig. 8
figure 8

Filtered profile (exaggerated) and first derivative to determine the notch locations

Full size image

The algorithm is based on the assumption that the notch can be approximated by a circle segment. The segment can be described by starting point, end point and radius, see Fig. 9. To determine the decisive circular approximation, various data points are examined as starting points and different radii are investigated. As possible starting points for the circle segment, the data points in the notch area are considered. The weld toes can be located by the extrema of the derivative of the filtered height profile, see Fig. 8. The notch area is defined in the range of 0.5 mm before and after the location of the maximum and minimum gradient. Since imperfections such as distortion and offset can occur, a regression line is determined with the data points of the base plate. A local coordinate system is then set and the coordinates are transformed to x' and z', see Fig. 9.

Fig. 9
figure 9

Decisive circle approximation with the notch radius \({r}_{best}\) and the flank angle \(\theta\)

Full size image

Subsequently, the decisive circle is approximated iteratively for all possible starting measuring points and possible radii between \(r\) = 0.1 mm and \(r\) = 5.0 mm in 0.01 mm steps. The full procedure of the algorithm is shown in Fig. 11.

For a considered starting point \(k= {DP}_{start}\) and a radius \(r\), the circle centre coordinates \({x}_{MP}\) and \({z}_{MP}\) are calculated orthogonal to the regression line. Next, the end point of the circle segment \({DP}_{end}\) is determined as the last data point inside the circle. The corresponding flank angle \(\theta\) can be determined by the circle tangent at the end point and the regression line.

The circular arc has to fulfil three criteria. The distance between the end point \({DP}_{end}\) and the start point \({DP}_{start}\) needs to be greater than 0.1 mm to avoid circular approximations outside the weld toe area. In addition, the distance of all measuring points in the notch to the circle \({\Delta r}_{i}\) must be less than 0.05 mm. This criterion ensures that the calculated notch radius is not too large and the circle segment represents the seam transition well. The criteria help to avoid erroneous circle approximations. However, the results of the algorithm are insensitive to changes of the criteria values. Furthermore, the circular arc has to be mapped with at least 5 data points, which corresponds to the recommendation given in [1]. Finally, the circle approximation is evaluated according to Zein el Dine [40] with the help of the quotient \({Q}_{k}\):

$$Q_k=\frac{\sum{\Delta r}_i}{n_{DP}^2}.$$
(4)

The distances of the measuring points in the notch to the circle \({\Delta r}_{i}\) are cumulated and divided by the square of the number of measuring points \({n}_{DP}\). A small quotient represents a good approximation of the real notch geometry. By squaring the number of measuring points, approximations with a large number of data points are preferred and notch radii based on fewer measuring points are avoided.

The starting point and radius combination with the smallest quotient leads to the decisive notch radius \({r}_{best}\).

2.5 Determination of the linear elastic notch factors

The filtered 2D scan data were used to determine the stress concentrations at the weld toes under tension load. Each side of the specimen has been scanned separately with 57 scan lines with a spacing of 0.5 mm. Due to the 3D tactile zero point setting the back and front scan data are compatible with high accuracy. For each scan line, a weld profile was composed from the data of the front and back side, see Fig. 10. The calculation of all notch factors was carried out fully automatically using ANSYS Mechanical APDL 17.2. The triangular version of the PLANE183 elements with quadratic displacement behaviour and six nodes per element were used for meshing. The element edge length at the scan lines was 50 μm to achieve sufficient accuracy with at least six elements in the notch, fulfilling the recommendations in [44, 45]. To determine the notch factors \({K}_{t}\), linear elastic material behaviour was applied with Young’s modulus E=210 GPa and Poisson’s ratio \(\nu=0.3\). The factor \({K}_{t}\) is calculated as the ratio of the maximum principal stress \({\sigma }_{1,max}\) to the nominal stress \({\sigma }_{n}\). The applied force was chosen to create a nominal stress of \({\sigma }_{n}=\) 1 MPa. It follows that \({\{K}_{t}\}=\left\{{\sigma }_{1,max}\right\}\) (Fig. 11).

Fig. 10
figure 10

Finite element model considering the scan data for the determination of the local notch stresses

Full size image
Fig. 11
figure 11

Evaluation algorithm for determining the notch radius, modified approach of Zein el Dine [34]

Full size image

3 Influence of deep rolling on weld geometry

The process shown in Fig. 5 was carried out for 27 butt welded specimens. The notch radii, flank angles and notch factors were evaluated fully automatically as described before. The data were determined for all notches and 57 scan lines each side before and after deep rolling. All 12,312 radii, angles and notch factors were analysed statistically. First, various statistical distributions were fitted to the data, see Fig. 12. The distributions were also evaluated with the Kolmogorov–Smirnov test [46, 47]. The p values as a result of the chosen goodness-of-fit test are found in Table 3. Commonly, a default significance level of 5% is used, which means that the null hypothesis is rejected if the p value is less than 0.05. Since all values in Table 3 are below this value, it means that at this significance level, no distribution passed the test. Nevertheless, it can be seen that the log-logistic distribution shows the largest p values for flank angle and notch factor and thus fits the data best. Figure 12 also shows that the log-logistic distribution best approximates the notch radius data as well. It seems that the log-logistic distribution is the most suitable distribution for all parameters. Similar results can be seen in [26, 28].

Fig. 12
figure 12

Comparison of statistical distributions for notch radius, flank angle and notch factor

Full size image
Table 3 Results of the Kolmogorov–Smirnov test (p value of hypothesis test)
Full size table

In order to investigate the influence of deep rolling on the weld geometry, the log-logistic distributions were compared for the data of the as welded and deep rolled condition, see Fig. 13 and Table 4. No significant influence of deep rolling on the flank angle can be quantified. In contrast, the distribution of the probability density function (PDF) of the notch radius changes. The scattering of the radii increased and slightly larger radii were determined. But, there is also a small shift towards smaller notch radii. Therefore, no clear positive effect on the geometry with regard to fatigue strength can be determined by the statistical distribution of the notch radii. In contrast, with the help of the FE simulations, it can be shown that the notch factors could be reduced by deep rolling, see Fig. 13. However, large notch factors up to \(K_t=4\) were still determined for the data of the deep rolled specimens. Based on these statistical evaluations the positive influence of deep rolling on the weld geometry cannot be stated with certainty for all specimens for the investigated deep rolling parameter combination.

Fig. 13
figure 13

Log-logistic distributions for the as welded and deep rolled condition of notch radius, flank angle and notch factor

Full size image
Table 4 Mean, variance and standard deviation of different probability distributions before and after deep rolling
Full size table

The parameters were investigated separately for all samples and for each notch. The weld parameters and the notch factors are compared in Fig. 14 exemplarily for one notch before and after deep rolling. It can be seen again that no significant influence of the deep rolling on the notch radius and the flank angle can be quantified. For the notch factor, on the other hand, a reduction over the entire width of the specimen can be seen.

Fig. 14
figure 14

Exemplarily course of notch radius, flank angle and notch factor along the weld toe before and after deep rolling

Full size image

The mean flank angle of the specimen shown in Fig. 14 is 29.9° and therefore lower than the mean value of all data (35.5°, see Table 4). The notch factor distribution of one notch with a mean flank angle of 42.8° is additionally depicted in Fig. 15. In contrast to Fig. 14, the notch factors along the weld seam could not be reduced by deep rolling. To investigate an influence of the flank angle on the deep rolling treatment, the data are evaluated notch by notch. For all lines, the differences \(\Delta {K}_{t}\) and \(\Delta r\) are calculated:

Fig. 15
figure 15

Course of notch factor along weld seam for a steep flank angle

Full size image
$$\Delta K_t=K_{t,as\;welded}-K_{t,deep\;rolled}$$
(5)
$$\Delta r=r_{as\;welded}-r_{deep\;rolled}$$
(6)

Afterwards, the mean values are determined for each notch and compared with the mean initial flank angle. The data scatter strongly for the difference of the notch radius as well as for the notch factor, see Fig. 16.

Fig. 16
figure 16

Influence of flank angle on reduction of notch radius and notch factors by deep rolling

Full size image

Nevertheless, a trend can be observed: With decreasing flank angle, the notch radii after deep rolling became larger and the notch factors could be reduced.

4 Discussion

The results presented show that with the selected combination of deep rolling tool and process parameters, the local weld geometry can only be influenced slightly by deep rolling. The determined initial and treated flank angles and notch radii scatter relatively strong along the weld seam of any specimen investigated. Therefore, it is difficult to quantify the influence of deep rolling on the local weld geometry with the parameters used. By using 2D FE simulations, a rather small reduction of linear elastic notch factors by deep rolling could be detected. However, it is evident that the initial geometry has a decisive influence on the treatment quality by deep rolling. Small flank angles approx. lower than θ=35 tend to allow rather pronounced treatment by deep rolling with the parameters used and enable improved elastic plastic deformation of the weld toe. Weld toes with large flank angles approx. higher than θ=35 are difficult to treat by deep rolling with the parameters used. It is assumed that the quality of the deep rolling process not only strongly depends on the initial weld toe geometry described by flank angle and notch radius but also on the deep rolling tool regarding its ball diameter db and deep rolling process parameters rolling pressure pr and overlap factor u. However, the results show that deep rolling with the parameters used only leads to small plastic deformations of weld toes compared to e.g. high-frequency mechanical impact treatment (HFMI). With these treatment methods, increases of notch radii up to ∆r=0.5mm and flank angles ∆θ=6 could be achieved in past studies [48, 49]. Nevertheless, the detected values for the single geometry parameters do highly depend on the measuring system and evaluation algorithm used, as mentioned above [1]. Additionally, high notch radii and flank angles generated by the HFMI-pin do not necessarily lead to a reduction of stress concentration due to the comparably high depth of indentation resulting in an undercut-like geometry [49].

5 Summary and outlook

This paper is about research work on post weld treatment with deep rolling to increase fatigue strength. The focus is on digitally supported experimental and numerical investigation methods. In addition, first findings regarding the influence of deep rolling on the local weld geometry were generated. For this purpose, a highly automated scanning method using a CNC machine tool in combination with an optical laser line sensor was implemented. This scanning method has a consistent process flow with a minimal amount of informational interfaces, resulting in 2D models true to the coordinate system of the machine tool.

In the future, the scanning method will be completed for a full reverse engineering process. The 2D scan data will be used to generate 3D volume models of the welds. These models will be used for 3D FE calculations to numerically calculate the fatigue resistance of the welded joints. Another possibility of the reverse engineering is a specimen adapted CAM planning of the deep rolling process, where the deep rolling is conducted following the local weld toe geometry in the x–y plane (see Fig. 14). The welding process leads to deviations of the beginning of the weld toe. Thus, while deep rolling in straight tracks, sometimes base material, sometimes material of the heat affected zone and sometimes filler material is rolled. These occurrences are leading to complex stress states in the treated material due to the different material properties and support effects while rolling the weld toe.

To explain these complex stress states, further investigations of the deep rolling process using the finite element method will be conducted. Furthermore, the numerical investigations shall determine a range of flank angles and toe radii which enable the rolling ball to achieve a more pronounced elastoplastic deformation of the weld toe. Additionally, the influences of different deep rolling process parameters on the resulting local residual stress state and the strain hardening of the subsurface will be investigated. The resulting subsurface properties derived from the process simulation will be used for the numerical calculation of the fatigue resistance of deep rolled butt welded joints. The numerical calculations regarding the fatigue resistance will be validated by experimental fatigue tests.

Further research will show the potential of deep rolling for high strength offshore construction steel.

The presented evaluation algorithm is currently part of a Round Robin study on the determination of weld flank angle and notch radius of the IIW Commission XIII-WG4. The aim is the investigation of the influence of evaluation method, operator and measurement device on the weld toe parameters.