Recommendations for the measurement of residual stresses in welded joints by means of X-ray diffraction—results of the WG6-RR test

Abstract

Residual stresses in welded joints are often of extended interest in order to evaluate unexpected failures or distortions. Since the possibilities to calculate residual stresses in welds are still strongly limited, the measurement techniques are still of great importance. Several measurement techniques with particular possibilities and limitations are available today where especially the different diffraction methods are used mostly. The material, weld type, and the size of the components are important for the quality of the results obtained with different methods as well as the environment where the measurements have to be carried out. The paper shall give an overview of the results of a round robin test on the application of XRD on butt welded joints which has been carried out in cooperation of different experienced laboratories. The results show the high reliability of XRD measurements in welds, if the measurements are performed under well-defined boundary conditions. The experiences can be used as a recommendation about useful measurement conditions the expectable quality of the results.

1 Introduction

Future developments of fatigue design rules will be forced to consider increasingly high-strength steels. The use of these materials depends strongly on the application of improved fabrication techniques which take into account the necessarily much higher quality requirements. Many techniques like the currently very popular high-frequency hammer peening procedure are founded on the generation of high-potential compressive residual stresses in order to enable strong fatigue strength improvements. On the other hand, it is well-known that residual stresses generally become more effective in materials with high ultimate strength. Consequently, the further development of the design rules must take also into account explicitly known residual stresses in welds due to different sources. This necessarily requires the control of the initial residual stress condition of welded structures as well as the possible changes of the residual stresses under service conditions.

While the numerical methods to calculate confidential residual stresses in welds are currently limited on very small and simple geometries the determination of residual stresses in welds requires experimental methods. Several techniques are applicable to determine residual stresses in welds [1, 2]. Mechanical techniques like the hole drilling, deep hole drilling, or the ring-core method use a locally restricted access to the material in order to measure the released strains which can be used to calculate the initial residual stresses. Completely destructive sectioning techniques like the contour method allow the determination of the initial residual stresses in the entire cross section with preference to the longitudinal residual stress component. Different non-destructive techniques like ultrasonic or micromagnetic method cannot directly correlate the measured signals to a particular strain or stress condition. The signals generally depend on the local material condition and require a calibration procedure which may complicate the measurements. The experiences of residual stress measurements during the last 50 years have evidently shown that the most reliable results can be expected by means of diffraction [3,4,5]. In addition to X-ray diffraction (XRD), also high-energy methods like neutron diffraction or the use of synchrotron radiation are well-established nowadays [6, 7] allowing a look in deeper zones or a much more sophisticated analysis of thin near-surface layers and different phase time- and temperature-dependent. Limitations for the practical use are the restricted access to the facilities which makes them more useful in fundamental research.

For the decision about the recommended method, first, the question about the use and the goal of the residual stress measurements is decisive. For instance, for the quality control of process parameters, often, surface measurements are sufficiently informative. The evaluation of mechanical and/or heat treatments requires the determination of residual stress depth distributions [8, 9]. In the neighbourhood of surface notches like weld toes, the residual stresses in the notches as well as the lateral residual stress profiles are in focus. If the quality of numerical calculations shall be evaluated by comparison with measured residual stresses through thickness, distributions in welded parts must be known. Finally, the time effort, the accessibility, and the resulting costs are also important for the decision if residual stress measurements are carried out or not.

In the RR test, experiments by means of X-ray diffraction (XRD) have been carried out by members of the IIW-Commission XIII-WG6. The goal was to work out the accuracy which can be expected in practical use when performing such measurements in welded joints. Here, the focus was fixed on butt welds with different weld geometries which already represents a non-trivial challenge for the accurate determination of residual stresses.

2 Background of the RR test on welds

2.1 Physical principles of XRD

The most suitable non-destructive methods for the determination of residual stresses are the diffraction techniques like X-ray diffraction (XRD), synchrotron diffraction (SD), and neutron diffraction (ND). The reason is that these methods determine the elastic deformation of the crystals which can be used unambiguously for the calculation of macroscopic strains and finally mechanical stresses using Hooke’s law. Since the elastic deformation primarily depends on the macroscopic elastic properties of the polycrystals which are not influenced strongly by local changes of the grain and heat treatment condition in the neighbourhood of a weld or in mechanically surface-treated metals, the reliability of the results is only depending on the availability of X-ray elastic constants. These constants can be easily calculated using E-modulus and Poisson ratio with a sufficient accuracy or with higher precision determined experimentally. For many technical materials and different radiations, these constants are indexed systematically. The experience shows that an explicit determination of these X-ray elastic constants for a particular application is not requested necessarily for standard materials like weldable steels.

The fundamental equation of the diffraction techniques is the well-known Bragg’s law:

$$ n\cdotp \lambda =2{D}_0\cdotp \sin {\theta}_0 $$

(1)

Here, D₀ is the distance of the lattice plane spacing of a certain {hkl}-lattice plane, λ is the wavelength of the incident beam, and Θ₀ is the corresponding diffraction angle. An elastic deformation of the crystal due to residual stresses or even load stresses changes the lattice spacing D₀ to D, and therefore, the resulting diffraction angle Θ₀ must be shifted to Θ. As the lattice spacing, D can be used to define a lattice strain.

$$ {\varepsilon}^L=\frac{D-{D}_0}{D_0} $$

(2)

The determination of the particular stress is possible with help of the measured D, if the stress-free lattice spacing D₀ is known. For an ideal single crystal, the stress-free lattice spacing can be calculated theoretically with help of the lattice parameter a, which is constant for each element. For technical materials, however, this will give not a reliable solution because D₀ can be shifted also in dependence on the interstition and substitution atoms as well as on second phases and on the dislocation and defect density. On the other hand, it has to be taken into account that the information, e.g., the strain measured with a single diffraction reflex as demonstrated in Fig. 1 is oriented perpendicular to the surface. The interesting residual stress components are in fact the components parallel to the surface because these components are assumed to interact with the mechanical load stresses. That means that if the penetration depth of the radiation is small (usually some microns with XRD), the information comes from a zone of the material where of course from the mechanical view, the stress in thickness direction must be zero due to the free surface, and the measured strain is only one component of the three-dimensional stress tensor.

Fig. 1

Principle of the diffraction of an incident beam at a certain lattice plane

From the practical view, the outcome of the very simplified described interrelationships can be summarized in the following possibilities to determine the residual stresses. Principally, the strains in three spatial directions should be determined to enable the calculation of the stress tensor or, on the other hand, reliable simplifications according the stress condition in the analysed volume are required and the stress-free lattice spacing must be determined experimentally. Especially, the last demand leads to high-precision requirements regarding to the applied equipment and as well on the measurement conditions. With regard to the rough conditions given by welded joints and as well to the size and the environment, it is hardly imaginable to use such methods for practical applications. However, the state of the art is that the different methods allow absolutely reliable results of residual stress determination experiments even though each method is connected with particular drawbacks and opportunities.

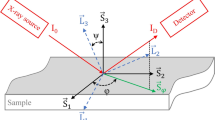
The most popular measurement technique in the technical practice is the X-ray diffraction method (XRD) which uses low-energy X-rays as the favourable radiation. The advantage of the method is that in comparison to other diffraction techniques, the required equipment is relatively cheap, the lateral resolution is relatively high, and the radiation protection can be reached very easy due to the low energy level (usually 30…40 keV). The most popular measurement and calculation method is the so called sin² ψ method which was developed by Fitzpatrick et al. [7]. Newer methods like the cos α method [10] will be used increasingly in future as well, but actually, there are less experiences, how the particular residual stress and surface condition affects the quality of their results. The sin² ψ method uses some general assumptions with regard to the material condition and the characteristic property of the low-energy radiation which is the low penetration depth in order to reduce significantly the efforts which are necessary for a reliable residual stress determination. The basic assumption is that in a polycrystalline technical metal, the crystals are oriented statistically disordered. As Fig. 2 demonstrates, the lattice spacing and the diffraction angle of a crystal depends on its orientation relative to the interesting stress direction (e.g., parallel to the surface). This means that under a constant local stress, the crystals will change their lattice spacings and the diffraction angle dependent on their orientation. Because the diffraction works selective and that is to say that the diffraction pattern is measured only in crystals with an orientation perpendicular to the normal between the incident and the reflected beam, it is possible to determine the diffraction angle in crystals oriented different to the stress direction by tilting the ψ angle. This is usually realized by moving the sample (irradiated area at the surface stands still in the center of the diffraction circle). As the strain can be defined with help of the shift of the lattice spacing (Eq. 2), the strains can be connected directly with the shift of the diffraction angle by deviating the Bragg equation.

$$ d\theta ={\theta}_0-\theta =\tan {\theta}_0\cdotp \frac{D_{\psi }-{D}_0}{D_0}\Longrightarrow \varepsilon =-\cot {\theta}_0\cdotp d\theta $$

(3)

If the conditions plane residual stresses, coordinate system parallel to the surface, polycrystalline material condition, e.g., diffracting crystals in any direction, isotropic material properties, no significant textures, and absence of strong residual stress gradients in the analyzed depth are fulfilled, the measurement problem is reduced on a very easy to handle procedure. As Fig. 2 reveals, the shift of the diffraction angle, and therefore, the strain depends linearly on the sin² of the concerning ψ angle. In this case, the residual stresses can be calculated by determining the slope m_φ of the 2Θ sin²ψ-regression line. The angle φ defines the measured direction in the defined surface coordinate system, and this is the direction of the observed residual stress component. An elastic constant ½ s₂ is required which can be approximated with a rather good reliability with help of the elastic constants E and ν, or it has to be determined experimentally with help of load stress measurements. The described basic conditions of the sin² ψ method are guaranteed in practice very often, because the penetration depth of the radiation is usually very small. Principally, the determination of peaks in two different ψ positions could be sufficient to determine the slope of the 2Θ/sin² ψ straight. However, in practice, 6 or more peaks in positive and negative direction each are usually examined in order to guarantee the linear 2 Θ/sin² ψ condition. It is obvious that the number of peaks defines finally the time effort for the determination of a single stress value. Newer variations of the XRD procedures use few ψ angles or the determination of the closed Debye-Scherrer rings (cos α method). The equipment is then much easier, and the duration of a single measurement can be reduced strongly, but the reliability and accuracy of these variations have not yet been proven sufficiently.

Fig. 2

Principle of the residual stress determination with help of the sin² ψ-method [5, 6]

2.2 Special problems of XRD application in welded joints

Residual stress determination in welded joints is usually complicated by different sources resulting from the change of the microstructure in combination with geometrical and fabrication-dependent features.

Geometrical changes like undercuts or sharp notch geometry at the weld toe and rough surface in the weld seam as well as bulging weld material lead to conditions where the device can be adjusted not perfectly. Then the focusing conditions may not be correct which leads to higher scattering range or to incorrect results. Slag rests or condensed metal dust may cover the surface at the interesting sites and cannot be removed always easily without mechanical effects at the surface. The generation of coarse grain in the weld seam and the heat-affected zone declines the amount of the reflecting crystals. Therefore, the exposure time must be extended strongly, but anyway, the scatter range of the results will arise. Sometimes, this problem can be solved by using a larger collimator and that is to say a lower local resolution, but frequently, in such zones, XRD measurements are not possible anymore. This problem is coming up often in welded Al- or Ni-based alloys or high alloyed steels.

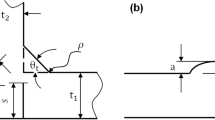
A simple problem is generated by the shape of the weld itself. As Fig. 3 illustrates, the weld material may build a barrier for the incident or the reflecting beam with regard to the measured location. In this case, an error will be unavoidable or at least the measurement is impossible. The grade of constraint depends obviously on the shape of the weld detail and on the welding procedure. In butt welds, the expected problems will be detachable as long as the height of the bulged weld material is not too high. Measurements in T joints or welds with fillet-welded longitudinal stiffeners are strongly complicated by the shape of the stiffeners and the weld seam. Here, the weld toe is the barrier and measurements are limited mostly on one ψ direction.

Fig. 3

Relationship between the weld shape and the beam geometry with regard to the accessibility of the sin² ψ-method

This limitation is a serious problem. As described, the measurement of the peaks at several ψ positions is a criterion for the grade of agreement between the defined conditions for the sin² ψ method. Another aspect is that under practical conditions, e.g., in welds with the described geometrical restrictions, the adjustment of the sample in precise ψ position 0 at the measured point is not always possible as required. Here, the movement in positive and negative ψ direction can solve that problem because the average value is then really reliable. Limitation on one direction on the other hand will lead to an error depending on the discrepancy at the zero position and finally to a more or less greater uncertainty of the determined residual stress value. However, it must be accepted that in welds with stiffeners, movement in both directions is impossible. Then, special attention must be paid for an adjustment of the sample as precise as possible.

2.3 IIW-WG6 round robin test on residual stress determination using XRD

2.3.1 Purpose of the round robin test

During discussions about the modus operandi how to handle residual stresses in a design process, two questions normally are coming up always. The first question is the possible and the required local resolution; the second is the question about the accuracy. An additional aspect which is important for the evaluation with regard to the fatigue performance is the stability or the amount of load-induced relaxation during the fatigue life because it is well-known that the efficiency of initial residual stresses (and this is valid for crucial as well as for beneficial RS) is the higher or the lower the grade of relaxation is. Therefore, it should be possible to repeat measurements during the fatigue life continuously in order to control possible changes or stability during the load history.

The first question of the required resolution can be answered easily because the general conditions are mostly defined by the devices and by the material. The technical range of applicable collimator diameters starts at approximately 0.3 mm and ends at some millimeter. The experiences of the practical application of XRD reveal that normally, collimator sizes lower than 1 mm lead to higher scattering and large extensions of the required exposure times. Diameters higher than 3 mm are not useful because lateral surface residual stress gradients in the surrounding of a weld seam may be smoothened strongly. In practice diameters, e.g., local resolutions of 1…2 mm are commonly used, because this is a good compromise between acceptable resolution and required time effort for exposure. Of course, this agreement is useful for standard arc welds, while in very narrow beam welds, this limitation may be not acceptable (Fig. 4).

Fig. 4

Influence of the collimator size on the local resolution of residual stresses and smoothing effect

The reliability of the measurement results depends of course on the grade of considering standard rules as it is good practice in other fields of material testing. Standard rules for XRD residual stress measurements are defined in [11]. These recommendations include standard rules for the measurement procedure, the calculation procedure, and useful material parameters which are used for the residual stress calculation. Furthermore, also, recommendations for the required calibration procedures are included. The careful consideration of the standard rules should guarantee that measured results are independent from the lab or the operator. This basic request was the initial idea of the presented RR test where the quality of typical residual stress determination in standard welds performed by different experienced labs should be demonstrated.

2.3.2 Participating laboratories

The RR test was carried out with six participants. Every lab is experienced in scientific and industrial application of XRD-analysis. Participants were the following:

• Institut für Werkstofftechnik - Metallische Werkstoffe und Fügetechnik; Universität Kassel

• Schweißtechnische Lehr- und Versuchsanstalt Halle

• Institut für angewandte Materialien - Werkstoffkunde (IAM-WK); Karlsruher Institut für Technologie

• CETIM - Senlis; France

• SONATS SA, Carquefou Cedex, France

• Institut für Füge- und Schweißtechnik, Technische Universität Braunschweig

• Montan Universität Leoben, Department Product Engineering

Additional measurements were carried out at the Berlin Synchrotron Facility (BESSY) using the EDDI beamline and with help of a portable diffractometer using the cos a method. The decision of the used devices was made by the different laboratories. In three labs, the measurements were carried out using portable diffractometers in three cases, and in the other labs, standard laboratories diffractometers were used.

2.3.3 Examined welds

The experiments were carried out using flat plates (200 × 150 × 6mm³) of a normalized fine-grained structural steel (German grade S460N) with a yield strength of 460 N/mm² (Fig. 5). The plates were plainly ground and stress relief annealed before welding at 600 °C/10 min. Two types of butt welds were produced: a TIG-welded dummy seam with a heat input of 10.92 kJ/cm and a GMA-welded dummy seam using a X90-filler material with heat input of 7.62 kJ/cm. As Fig. 6 shows, the TIG-process generates a very flat weld seam, while the MAG-process leads to a strongly bulged weld seam with difficult geometrical measurement conditions. Due to the relatively low heat input, the hardness values in the heat-affected zone (HAZ) are rather similar. Larger discrepancies can be observed in the weld material which shows the influence of the lower strength filler material of the MAG-weld. This is shown also by the distribution of the FWHM values of the measured diffraction lines (Fig. 7) which evidently illustrates the influence of the different strength properties.

Fig. 5

Shape and dimensions of the used samples (S460N)

Fig. 6

Weld geometry and structure of the TIG- and the MAG-weld and hardness distribution

Fig. 7

Near-surface hardness distributions and distributions of the {211}-FWHM values of the measured diffraction lines

3 Results of the residual stress measurements

Figure 8a shows the representative distributions of the longitudinal and transverse residual stresses across the weld seam of a TIG-welded sample determined with a commonly used collimator-Ø of 1.0 mm. Here, the typical symmetrical residual stress profiles are observed with some minor discrepancies in the weld material and the typical maximum and minimum peaks in the transition zone between the weld and the parent material. The average measurement error is below 10 MPa except in the weld seam where an error level of 50 MPa is reached. The error of the transverse residual stresses is necessarily higher. The reason is that due to the shift of the ψ angle, the geometry of the irradiated area changes with ψ, and therefore, the measured value is more influenced by the stress gradient. In longitudinal direction, the interval of the stress gradient is constant which leads to a lower error.

Fig. 8

a Representative residual stress profiles of the investigated samples (left hand side) and related measurement errors (right hand side); GTA-weld. b Representative residual stress profiles of the investigated samples (left hand side) and related measurement errors (right hand side); GMA-weld

The residual stress profiles of the MAG-welded sample are shown in Fig. 8b. The related error in the weld seam is lower than in the TIG-welded sample although the shape of the weld seam is not ideal for the measurements. Nevertheless, the lower strength of the weld material in combination with the finer grain structure leads to improved diffraction conditions with the consequence of a smaller measurement error.

3.1 Influence of the local resolution on the quality of the measurement results

The influence of the local resolution on the measured residual stress profiles is represented in Fig. 9a and b. In Fig. 9a, the profiles obtained using collimators with diameters from 0.5 to 3.0 mm are compared. The measured results are obviously independent from the collimator size except the smallest diameters of 0.5 and 0.8 mm. Here, a greater discrepancy in the weld material is present. However, the deflection of the profiles with particular peaks and tales in the transition zone between the weld and the parent material is marginal in longitudinal and in transverse direction. In Fig. 9b, the profiles of the average values with the related error bars are shown. Evidently, the divergence in the weld seam is below ± 30 N/mm². This result is of great importance because it demonstrates that the residual stresses in arc welds can be measured with a good accuracy without the requirement of very high local resolution. Since the local resolution is very important for the exposure time and that is to say for the time effort for a single measurement, this results offer the possibility to determine residual stresses in welds in an acceptable time span.

Fig. 9

a Comparison of the residual stress profiles measured with different local resolutions (collimator-Ø) in a TIG-welded specimen. b Average residual stress profiles with related error bars (scattering range)

3.2 Results of the RR tests

In Fig 10a, the residual stress distributions measured in TIG-welded plates by the participating lab results using uniform collimator sizes of 1.0 mm Ø are shown. As the resulting average profiles with the resulting scatterband reveal (Fig. 10b), the scatter range in the base material and in the heat-affected zone is between ± 25 N/mm² and ± 40 N/mm². In the weld seam, increasing deviations with an amount of upt to ± 100 N/mm² are present. Nevertheless, the agreement of the obtained residual stress profiles can be interpreted as excellent. Experiences with larger numbers of specimen of the same series have shown that the variation of the residual stresses in welds may vary between ± 20 and ± 80 N/mm² even if the specimen have been produced under comparative laboratory conditions. Considering this unpreventable variation, the agreement of the obtained results is quite good.

Fig. 10

a Comparison of the residual stress profiles obtained by the participating laboratories in TIG-welded samples. b Average residual stress profiles and related scatter ranges. c Comparison of the measured and normalized profiles of the integral width of the diffraction lines samples

Larger deviations of the different measurements are connected with the integral width of the measured diffraction lines (Fig. 10c, left hand side). This is not really surprising because these values are much more influenced by the particular devices and assessment procedures (detector type, beam geometry, peak smoothing, etc.). If the determined integral widths are normalized using the corresponding values of the base material, this error is reduced significantly. Nevertheless, in the weld material, a greater discrepancy must be accepted.

Almost the same results are worked out for the MAG-welded samples with a bulge weld seam (Fig. 11a). Here, the span of the observed deviations is below a range of ± 20 N/mm² in the parent material and in the heat-affected zone. Additional measurements, which shall clarify if this is a single measurement error or a larger disagreement between the residual stresses in this sample, are in progress. Finally, the residual stresses determined in the weld seam show a larger scatterband. The variation of the residual stresses (transverse and longitudinal, Fig. 11b) is between ± 100 N/mm² in the weld material. As Fig. 12 shows, the distributions of the integral width of the diffraction lines demonstrate again the laboratory or device-specific influence. After normalizing the measured values in relation to the base material, the results are rather uniform with a lower discrepancy in the weld material (Fig. 12).

Fig. 11

a Comparison of the residual stress profiles obtained by the participating laboratories in MAG-welded samples. b Average residual stress profiles and related scatter ranges

Fig. 12

Comparison of the measured and normalized profiles of the integral width of the diffraction lines samples

4 Summary and conclusions

The determination of residual stresses by means of X-ray diffraction is the most suitable technique if confidential results are expected without any detraction of the investigated components even under rough or difficult environmental conditions. However, the accuracy and the reliability of the obtained results depend strongly on the adherence of some standard [11] rules considering the special requirements of welds:

• A sufficient number of ψ angles are required to eliminate the disturbing effects of coarse grain and unsteady surface in the irradiated area in the surrounding of the weld seam.

• A measurement in both positive and negative ψ direction is generally recommended. Since in the weld seam, the accurate position of each ψ angle cannot be guaranteed sufficiently good, the consideration of both directions enables a compensation of this adjustment error.

• In welds with particular limitations due to the bulged weld seam or shading stiffeners, where measurements cannot be performed in both ψ directions, a higher precision for the adjustment is required.

• In a technical useful range, the chosen resolutions do not affect strongly the accuracy of the measured residual stresses. Especially, in the weld seam, the detrimental effect of the grain structure compensates the benefit of a higher resolution and lower smoothing effect by a higher scatter range. Useful collimator sizes of 1… 2 mm combine a sufficient local resolution with a lower error and an acceptable exposure time.

If the described standard rules of XRD are respected and the same elastic constants are used in welded joints, repeatable measurement results within a range of ± 50 N/mm² or better can be expected independent from the operator or the used equipment. This is in the range where the initiated residual stresses in equivalent welds may vary. This perception is applicable for conventional arc welds with technically usual weld seam geometries. Approval of a general applicability for welds including small beam welds and comparable should be given separately.