1 Introduction

Rectangular hollow sections (RHSs) usually offer good, or at least moderate, structural performance for beams subjected to various loads, such as axial and shear forces as well as bending and torsional moments. In warping, the cross section of the beam remains in its original shape, whereas in distortion, it will take on a parallelogram shape. Both these deformations cause axial displacements and/or membrane stresses in the beam, but distortion also causes transverse bending stresses in the wall of the cross section. These phenomena are independent degrees of freedom of the beam. Particularly from the fatigue design point of view, the bi-moment causing the warping of the cross section and distortional loads of RHS beams is an interesting, but lesser known load condition. The fundamental basics of the primary warping of box beams can be found, e.g., in Ref. [1,2,3,4], while the secondary warping of the cross section is covered in Ref. [5,6,7]. Rubin [8] studied the effect of the corner radius on the primary warping of RHSs, showing that it also causes primary warping in square hollow sections (SHSs). Meanwhile, the distortion of closed cross section has been studied in Ref. [9,10,11,12]. Nevertheless, previous studies tend to focus on the theoretical background of the distortion and warping of cross sections, and less attention has been paid to practical analysis and design proposals to prevent fatigue failure due to warping and distortion. In weight-critical beams, the use of ultra-high-strength steels (UHSSs) with yield strengths up to 1100 MPa becomes reasonable. With UHSS grades, hot- or cold-formed profiles are not typically available, and box beams made from welded sheet metals are used instead. In such structures, the fatigue-critical details are the brackets, longitudinal welds, and transverse welds fixing the beam to the end plate.

The present paper introduces an analytical approach to calculate the stresses that can be used in the fatigue analysis of a cantilever beam. First, the bi-moment and warping stress distributions along the beam length and over the cross section are obtained and, subsequently, the distortional behavior is established based on the theory of a beam on an elastic foundation (BEF) [13]. Finite element analyses (FEAs) using 2D mid-plane element models are conducted to obtain numerical results for a comparison. In addition, a more detailed analysis of the secondary warping of a square hollow section (SHS) with a round corner is conducted using a 3D solid element model. A fatigue analysis is conducted on the end plate of a cantilever beam using the effective notch stress (ENS) concept [14] and considering both weld toe and weld root fatigue failures. Furthermore, with FE modeling, the effect of a transverse diaphragm plate and its location on the distortion of the cross section is investigated; this is followed by some design recommendations. The work is focused on beams loaded with torsional moment, and therefore, SHS profile is the main focus of this work. In addition, RHSs are also analyzed to provide a comparison with an SHS.

2 Analytical approach

2.1 Geometry, load, and boundary conditions of a cantilever beam

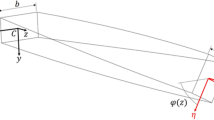
In this study, the force couple loading F is imposed on pair of brackets at the free end of a cantilever beam, as illustrated in Fig. 1. The other end of the beam is fixed to a stiff end plate, thus representing a completely rigid boundary condition. The loaded end of the beam is provided with a diaphragm plate, preventing the distortion of the cross section in the place where the brackets are fixed to the beam. However, as the plate is very thin, it does not prevent the free warping of the beam in this section.

Fig. 1
figure 1

The studied and analyzed box beam structure

Full size image

2.2 Warping due to torsional loading

Using the cross-section symbols denoted in Fig. 1, for a thin-walled closed section with constant plate thickness t, the torsional moment of inertia It is

$$ {I}_t=\frac{4{A}_0^2}{\underset{s}{\oint}\frac{ds}{t}}=\frac{4{b}^2{h}^2}{\sum \limits_i\frac{s_i}{t_i}}=\frac{2{b}^2{h}^2t}{b+h} $$
(1)

The warping constant of the cross section Iω consists of primary and secondary parts, whereby the primary part is calculated based on the sectorial coordinate ω of the middle line of the cross section and the secondary part is based on the warping over the plate thickness in direction rn for each cross section part.

$$ {I}_{\omega }=\underset{s}{\oint }{\omega}^2 tds+2\underset{s}{\oint}\underset{r_n=0}{\overset{t/2}{\int }}{r}_n^2{s}^2{dr}_n ds=\underset{s}{\oint }{\left({r}_t-\frac{2{A}_o}{t\underset{s}{\oint}\frac{ds}{t}}\right)}^2 tds+\underset{s}{\oint}\frac{t^3}{48}{s}^2 ds=\frac{b^2{h}^2t}{24}\frac{{\left(h-b\right)}^2}{h+b}+\frac{2\left({b}^3+{h}^3\right){t}^3}{144} $$
(2)

In the case of SHS, the dimension h = b and, consequently, primary warping is zero; however, except for a rotationally symmetric cross section, there always exists secondary warping, which for an SHS with sharp corners is:

$$ {I}_{\omega }=\frac{b^3{t}^3}{36} $$
(3)

In general loading cases, the beam can be subjected to both axial and transverse (shear) loads and thus also bending moments. Nevertheless, the main focus of this study is on the torsional moment T caused by the couple force F as follows:

$$ T={Fb}_b $$
(4)

The torsional moment T in the brackets generates the bi-moment Bω,0 at the loaded end of the beam:

$$ {B}_{\omega, 0}= Tc={Fb}_bc $$
(5)

The bi-moment depends on the second derivate of the twisting angle θ relative to the x-axis.

$$ {B}_{\omega }(x)={E}^{\hbox{'}}{I}_{\omega}\frac{d^2\theta }{dx^2}=E\left[\frac{b^2{h}^2t}{24}\frac{{\left(h-b\right)}^2}{h+b}+\frac{2\left({b}^3+{h}^3\right){t}^3}{144\left(1-{\nu}^2\right)}\right]\frac{d^2\theta }{dx^2}, $$
(6)

where E and v are the Young’s modulus and the Poisson’s ratio of material, respectively. The bi-moment of the beam consists of Bω,0 and the effect of the torsion moment T. Considering the present boundary and load conditions, as shown in Fig. 1, the bi-moment distribution Bω, (x) over the beam length can be defined:

$$ {B}_{\omega }(x)=\frac{B_{\omega, 0}\cosh k\left(L-x\right)+\frac{T}{k}\sinh kx}{\cosh kL}={Fb}_b\frac{ck\cosh k\left(L-x\right)+\sinh kx}{k\cosh kL}, $$
(7)

where the torsion constant k is

$$ k=\sqrt{\frac{GI_t}{EI_{\omega }}}=\sqrt{\frac{I_t}{2\left(1+v\right){I}_{\omega }}} $$
(8)

In Eq. (8), G is the shear modulus of material. At the loaded end of the beam, Bω,x = 0 = Fcbb, and at the fixed end:

$$ {B}_{\omega, x=L}={Fb}_b\frac{ck+\sinh kL}{k\cosh kL} $$
(9)

The bi-moment induces axial stresses in the beam, which consists of membrane stresses due to the primary warping and shell bending stresses due to the secondary warping. For an SHS with sharp corners, the following equations can be derived:

$$ {\displaystyle \begin{array}{l}{\sigma}_{\omega }(s)=\frac{B_{\omega }(x)}{I_{\omega }}\omega =0\ \\ {}{\sigma}_{\omega}\left(s,{r}_n\right)=\frac{36{B}_{\omega }(x)}{b^3{t}^3}{sr}_n=\pm \frac{9{B}_{\omega }(x)}{b^2{t}^2},\mathrm{at}\ \mathrm{the}\ \mathrm{outer}\ \mathrm{or}\ \mathrm{inner}\ \mathrm{corner}\ \mathrm{of}\ \mathrm{the}\ \mathrm{SHS}\hbox{-} \mathrm{profle}\ \end{array}} $$
(10)

This torsional moment T consists of the pure (or uniform) torsion TBredt and the warping torsion Tω.

$$ T={T}_{Bredt}+{T}_{\omega }={GI}_t\frac{d\theta}{d x}+{EI}_{\omega}\frac{d^3\theta }{{d x}^3} $$
(11)

The shear stresses involved in warping can now be defined as

$$ {\tau}_{\omega }=\frac{T_{\omega }{S}_{\omega }}{I_{\omega }t}=\frac{dB_{\omega }(x)}{dx}\frac{S_{\omega }}{I_{\omega }t}={Fb}_b\frac{\cosh kx- ck\sinh k\left(L-x\right)}{\cosh kL}\frac{S_{\omega }}{I_{\omega }t}, $$
(12)

where Sω is the sectorial cross section modulus. Based on Bredt’s formula, the shear stress is

$$ {\tau}_{Bredt}=\frac{T_{Bredt}}{2 bht}=\frac{T-{T}_{\omega }}{2 bht}=\frac{Fb_b}{2 bht}\left[1+\frac{ck\sinh k\left(L-x\right)-\cosh kx}{\cosh kL}\right] $$
(13)

The schematic distributions of internal forces over the beam length and the warping stresses over the cross section area are presented in Fig. 2. In the case of SHS, the bi-moment will occur only at the loaded and fixed ends of the beam.

Fig. 2
figure 2

a Bi-moment and b torsional moment distributions over the beam length, c primary and secondary warping stresses at the corner of an RHS cross section, and d Bredt’s and warping shear stresses in the cross section of an RHS

Full size image

The secondary warping occurs very locally in the corners of the box section, but it can induce detrimental stresses if the local degree of freedom, involved in the secondary warping, is prevented. This can occur when the wall of the cross section is locally prevented to rotate, e.g., due to joining the beam by welding to a stiff transverse plate component. It is worth noting, however, that the primary warping stresses depend on the global boundary conditions of the beam, while the secondary warping stresses depend on the local boundary conditions of the cross-section wall. Consequently, primary and secondary warping can occur independently on each other. The primary warping of the cross sections with round corners has been investigated analytically by Rubin [8]. In this study, this issue is addressed by means of the FEA in Sect. 3.

2.3 Distortion of the beam

In addition to the warping, the torsional load, causing the local bi-moment at the loaded end of the beam, also establishes a distortional loading. Unlike with the warping, in the distortion, the cross section does not remain in its original form but deforms to a parallelogram shape. Because the corners of the box section are rigid, the distortion causes transverse bending stresses. Both warping and distortion includes longitudinal deformations and stresses, whereby the distributions along the profile perimeter are affine yet disassociated in the longitudinal direction of the beam. Based on the theory of BEF, Fig. 3 shows the longitudinal and transverse distributions of distortion, which are compared in some cases with the results of the numerical analyses described in Sect. 3. The distortional deformation v(x) (= d1 − d2, see Fig. 3) is the difference between the diagonal dimensions of the cross section as defined by the deformed geometry. The distortional deformation in the longitudinal direction of the SHS beam with a semi-infinite length can be determined based on the theory of BEF [15]:

$$ v(x)=\frac{12\sqrt{2}{e}^{-\beta x}\sin \beta x}{\beta^2{Etb}^3} Fc, $$
(14)

where

$$ \beta =\sqrt[4]{\frac{12{t}^2}{b^6\left(1-{\nu}^2\right)}} $$
(15)
Fig. 3
figure 3

Distortion of the SHS beam (L = 4000 mm) with a cross section with the dimensions 240 × 240 × 4 mm loaded with a force couple of F = 150 kN (bb = 240 mm, c = 100 mm); based on the theory of BEF: a distortional deformation, b transverse bending stress (σb) at the corner, and c longitudinal membrane stress (σv) at the corner, obtained following the analytical approach and FEA. Further details regarding the FEAs can be found in Sect. 3

Full size image

The elastic foundation constant f for the BEF approach can be defined by analyzing the cross section as a continuous frame and calculating the transverse stiffness of the frame based on the unit force-displacement-method.

$$ f=\frac{4{Et}^3}{b^3\left(1-{\nu}^2\right)} $$
(16)

The maximum deformation vmax occurs when

$$ \frac{dv}{dx}=\frac{4\sqrt{2}{\beta}^2{e}^{-\beta x}\left(\sin \beta x-\cos \beta x\right)}{f} Fc=0\to \tan \beta x=1\to {x}_{v_{\mathrm{max}}}=\frac{\arctan 1}{\beta }=\frac{\pi }{4\beta }=\frac{\pi }{4}\sqrt[4]{\frac{1-{\nu}^2}{12}}\sqrt{\frac{b}{t}}b $$
(17)

If the distortion occurs due to fluctuating torsion, it can be a detrimental phenomenon leading to the fatigue of longitudinal welds if they are located in the corners of the box beam. The longitudinal welds (all or at least some) are typically prepared using single-sided welding and, thus, the weld root fatigue capacity may become a critical design criterion. The phenomenon can be diminished through the use of diaphragm plates; however, this effect only occurs locally. Naturally, the first diaphragm plate is located at the fixing point on the brackets, at the loaded end of the beam. However, this plate prevents the distortion of the cross section only at that position. Along the beam, the distortion v(x) increases according to Eq. (14), reaching a maximum at the distance of π/(4β) and, subsequently, fading gradually. A simple engineering design concept could indicate placing of a second diaphragm at precisely the place of maximum distortion. Theoretically, the optimal location for an additional diaphragm could be determined using the theory presented by Hetényi [13], but this requires very complicated analytical formulation and is, therefore, ignored here. However, the optimal location of the second diaphragm plate is investigated numerically by means of FEAs in Sect. 3.

The transverse bending stress σb(x) follows the distribution of distortional displacement v(x) and is

$$ {\sigma}_b(x)=\frac{3 Et}{2\sqrt{2}{b}^2\left(1-{\nu}^2\right)}v(x) $$
(18)

The longitudinal membrane stress of the beam σv(x) follows the second derivative of the displacement and, consequently, can be calculated using the following equation:

$$ {\sigma}_v(x)=\frac{3{e}^{-\beta x}\cos \beta x}{tb^2} Fc $$
(19)

3 Numerical analysis

3.1 FE model

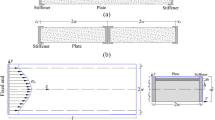
The FE model for a beam with the load and boundary conditions is shown in Fig. 4. The beam is made of steel material and, thus, E = 210 GPa and v = 0.3. Linear 4-noded plate element (CQUAD4) models with linear static analyses are carried out using NxNastran as a solver. More detailed descriptions of the models and analyses are given by Ahlfors [16, 17]. A beam length of L = 2000 mm was used as the basis in the analyses. However, to validate the analytical approach (see Sect. 2), in which a semi-finite beam was assumed, an L = 4000 mm model (240 × 240 × 4) was analyzed to also take the damping effect (e−ßx) into account in the FEA. The results of those analyses are presented in Fig. 3. Furthermore, linear 8-noded solid element (CHEXA) models were used to investigate the secondary warping of the cross section and to analyze the welded end plate detail using the ENS concept. The element mesh models used in the analyses can be found in Sect. 3.2.

Fig. 4
figure 4

Dimensions of the SHS beam used in the FEA

Full size image

3.2 Warping of the cross section

In an SHS beam with sharp corners, the deformations and stresses due to primary warping are zero. However, secondary warping occurs at the fixed end of the beam. A general overview of the normal stress distribution in the fixed corner and the same stress distribution in the inner, middle, and outer surfaces of the profile face derived using both plate and solid elements are shown in Fig. 5 a and b, respectively. The adjacent normal stress components in the horizontal and vertical plates are opposite and, thus, induce high local shear stresses in the corner acting parallel to the longitudinal axis of the beam. The normal and shear stresses occur only locally and have no impact on the static capacity of such a beam structure, but they must be considered in fatigue analysis because they can have a remarkable negative role on the structural performance and durability.

Fig. 5
figure 5

a General overview of normal stresses due to secondary warping in a sharp corner of an SHS and b distributions of the same stresses along the inner, middle, and outer surfaces of the profile [17]

Full size image

If the box section has round corners, there also exist, in addition to secondary (bending) stresses, primary (membrane) stresses due to the warping of the SHS. Figure 6 depicts the typical stress distribution of an SHS profile and the effect of the corner radius to beam height ratio on the degree of primary warping in the corner area. If the corner radius to height ratio of profile (r/h) approaches zero, the primary warping will vanish, and if the ratio approaches a value of 0.5, all warping will vanish. Figure 6 b shows that the maximum warping is reached when r/h = 0.18.

Fig. 6
figure 6

a Axial stress distribution at the fixing point and b the effect of the corner radius to height ratio on the degree of warping of the SHS 150 × 150 × 8 [17]

Full size image

Figure 7 shows the ratio of normal stress to Bredt’s shear stress along the profile perimeter for the SHS and RHS profiles. It can be seen that in the corner area, the axial membrane stresses can be approximately half the shear stresses.

Fig. 7
figure 7

Membrane stress to shear stress ratio for a SHS 150 × 150 × 8 and b RHS 200 × 100 × 8 beams subjected to pure torsion loading [17]. Parameter s is the distance along the center line of profile perimeter and the stress distribution is presented for one quarter of the whole cross section

Full size image

To consider the fatigue of the SHS with a round corner, the effective notch stress (ENS) concept [14] was applied to a 3D geometry, with modeled welds and a reference radius of rref = 1.0 mm at the weld toe and root, in the joint where the highest axial stress occurs, as illustrated in Fig. 8a. The dimensions of the profile are given in the Fig. 8b.

Fig. 8
figure 8

a SHS detail analyzed with the ENS method and b the dimensions of the analyzed SHS profile (modified from [17])

Full size image

The results of the analyses are presented in Fig. 9. The weld throat thickness a ≈ 1.1 t was equal in all FE models, but the degree of penetration was varied so that the models represented joints with fully and half penetrated as well as pure fillet welds. In all cases, the weld toe is the critical part of the joint, not the root side. Consequently, the stress distributions over the plate thickness are presented only at the weld toe. The presented distributions are normalized by dividing the normal stresses by Bredt’s shear stress.

Fig. 9
figure 9

Stress ratio distributions over the plate thickness at the weld toe with different degrees of penetration: a full penetration, b half penetration, and c pure fillet weld [17]

Full size image

3.3 Distortion of the cross section

In Fig. 10, the deformations for different profile sizes are presented for a beam length of 2000 mm.

Fig. 10
figure 10

Effect of the profile cross section dimensions on the distortion of the beam [16]

Full size image

In Fig. 10, it can also be seen that some of the distortions of the beam are at the location of the first diaphragm plate (x = 0). This is due to the shear deformation of the diaphragm plate, of which thickness is tp.

$$ {v}_0=\gamma b=\frac{\tau b}{G}=\frac{Fb}{Ght_p}=\frac{150000\cdot 240}{80000\cdot 240\cdot 4}=0.47\mathrm{mm} $$
(20)

Figure 11 presents the effect of the plate thickness t on the distortional deformation of the SHS profile with the dimensions 240 × 240 × t. A 50% increase in the plate thickness decreases the deformation nearly by approximately 50%. This cannot be concluded directly from Eq. (14) since the thickness t is involved in the β parameter.

Fig. 11
figure 11

Effect of plate thickness and the location of the second diaphragm plate on the distortion of the cross section [16]

Full size image

Figure 11 also demonstrates the effect of the location of the second diaphragm plate in the SHS beam with the aforementioned dimensions. The optimum location for the distance seems to be roughly the dimension of the beam height. Figure 12 shows the effect of diaphragm plates on the axial stresses of the SHS and RHS beams. The transverse plates slightly prevent the warping deformation, acting as internal springs for the bi-moment, but locally, they prevent the distortion efficiently.

Fig. 12
figure 12

Longitudinal membrane stresses (σv) for a SHS 240 × 240 × t and b RHS 340 × 240 × t [16]

Full size image

4 Discussion

The normal and shear stresses due to warping and distortion cannot be neglected in structures subjected to torsional loading. Distortion should always be considered in the analysis of flexibility, stability, fatigue, and ultimate capacity of joints with hollow sections. In the present paper, the distortion and warping behavior of SHS and RHS members subjected to torsional moment were investigated analytically on the basis of theoretical model for stress analysis and, numerically, conducting FEAs.

The length of a beam structure plays a crucial role in the warping and distortion distributions along the beam length. In RHS beams, the primary warping is typically rather small (if h/b < 2) and the local peak value occurs only at the loading and fixing points of beam, as illustrated in Fig. 2. The distortion has its maximum at distance of 0.412b√(b/t), after which it fades very smoothly, as illustrated in Fig. 3. Even a 4000-mm-long beam with the cross-section dimensions 240 × 240 × 4 mm is not long enough to completely eliminate the distortional deformations and stresses. This causes small differences between the theoretical model and the FEA, see Fig. 3, but generally, the agreement between the analytical and FEA calculations is good.

Stresses due to warping and distortion can have a remarkable effect on the fatigue performance of a beam subjected to cyclic or fluctuating torsional loading. The primary warping, due to the round corner together with secondary warping, can cause fatigue failures even in the case of SHS, as shown in Fig. 13a. The distortion-induced cyclic transverse bending stresses, see Fig. 3b and Eq. (18), can also cause fatigue failures longitudinally at the corner of SHS members, as demonstrated in Fig. 13b. Particularly, in the case of UHSS materials, fillet-welded hollow sections are fabricated for steel constructions, e.g., in boom components, due to the lack of tubular members made of high- and ultra-high-strength steel grades. In such welded details, lack of weld penetration and sharp transition at the weld root expose the longitudinal welds for weld root fatigue failures. Consequently, careful consideration of cyclic torsional loads in the stress analysis is particularly required in welded box beams. In Ref. [18, 19], fatigue failures in an SHS with an end plate, and subjected to the cyclic torsional moment, were found due to the warping and distortion. Nevertheless, these studies did not address the warping behavior in more detail.

Fig. 13
figure 13

Warping-induced fatigue failures in a SHS beam with the cross section dimensions of 100 × 100 × 5 mm subjected to cyclic torsional loading: a fatigue failure at the weld toe of an end plate and b longitudinal fatigue crack at the corner of a SHS member [18]

Full size image

The diaphragm plate at the loaded end of the beam does not prevent distortion, although it does curtail it locally. When considering the optimal location for stiffeners and diaphragm plates, these are usually located where the maximum deformation occurs without such stiffener, see Eq. (17). On the basis of the results of this study, see Fig. 11, this approach is not applicable when considering the warping behavior. If diaphragm plates are located too far from each other, the distortion occurs between the diaphragm plates, and if they are too close, the effectiveness of the second plate is insufficient. The second plate after the end plate is important because it creates a transverse torsion bar inside the beam, which connects the torsional couple moments. The stiff torsion bar efficiently destroys the bi-moment induced by the couple forces in the brackets. A transverse bar in the shape of any closed hollow section, as illustrated in Fig. 14, is stiff and will efficiently eliminate the bi-moment loading by causing torsion shear stresses in the transverse box. This grounding spring effect is addressed in greater detail in Ref. [20]. The effectiveness is based on the torsional stiffness St,p of the transverse beam created by these diaphragm plates and can be evaluated using the following equation:

$$ {S}_{t,p}=\frac{GI_t}{b}=\frac{2{Gh}^2{l}^2}{b\left(\frac{h}{t_p}+\frac{l}{t}\right)} $$
(21)
Fig. 14
figure 14

The bi-moment is grounded by a square or b circular shapes, which can be created by diaphragm plates, separate tubes, or castings

Full size image

The recommended distance for the second diaphragm plate still enables the welding, also in a case of commercially available RHS beams. If the box section is self-made design, the diaphragm can be welded from three sides before closing the section, which also enables longer distance for the second diaphragm.

5 Conclusions

Based on the theoretical and numerical analyses along with experimental findings from the literature, the following conclusions can be drawn:

  • Primary warping (causing either axial membrane stresses or deformations) occurs also in SHSs with round corners.

  • Primary and secondary warping should be considered in the fatigue analysis of SHSs subjected to fluctuating torsional loading, particularly at the rigid fixed end.

  • Distortion can have effect on the flexibility, stability, and ultimate capacity of joints, also in static loading.

  • Transverse bending stresses due to distortion can have a negative impact on the fatigue performance of beams with hollow cross sections, especially if the fixing welds are located in the corners of the cross section.

  • A diaphragm plate located only at the loaded end does not prevent distortion in a beam.

  • A second diaphragm plate efficiently decreases the distortion if it is located at a distance of approximately the height of the beam from the end plate.

  • In the fillet-welded detail at the fixed end, higher stresses resulted at the weld toe than at the weld root, also in pure fillet welds with no penetration.