1 Introduction

Brazing in a continuous belt furnace is a quite cost-effective way of manufacturing components. This joining technique is used in the manufacturing of many applications, like heat exchangers, heating and cooling systems, as well as in the common rail systems for common rail direct fuel injection. In rails, brazing is the unrivaled joining technique since numerous (in rails up to 20) connections can be joined in one single process, typically using continuous belt furnaces.

Many brazed components, such as heat exchangers or rails for gasoline injection, experience cyclic loading during service. The loading is typically complex: Variable amplitude loading with variable mean stresses are acting at the components. For some application, the load cycles reach rather high values (N ≈ 109) throughout the lifetime. Additionally, complex loading conditions such as multi-axial stress states and corrosion have to be considered. All components have to be designed to withstand the complex loading condition during the planned service life.

The automotive industry has the urge to reduce the components’ wall thickness for economical reasons. Additionally, the pressure in common rails application needs to be increased in order to reduce the exhaust emissions and to meet legal and environmental requirements. This diametrical challenge requires a reliable and safe design of these thin-walled components in order to prevent a premature failure due to fatigue cracks. Especially if these components are safety-relevant, failure during service has to be prevented. A fatigue crack in the injection system in a rail would lead to a leakage of gasoline with hazardous consequences.

In the current industrial practice, the design process often relies on experimental data from fatigue tests and experiences from previous components with a similar design. This approach to obtain a reliable and safe design is often time- and cost-consuming, especially if components fail in the prototype state. Then, the components have to be redesigned, new prototypes have to be manufactured, and additional tests have to be performed. A reduction of the development time and cost can be achieved if a fatigue assessment approach is available that enables a safe life of the components already in the design phase.

In many publications, the fatigue strength of brazed specimens has been investigated. In these publications, mostly ground joints were used in order to identify the influence of brazing conditions like brazing temperature and brazing time [24], the influence of a post-braze heat treatment [7, 22], the influence of defects [9, 15, 19], or the influence of corrosive environment [16] on the fatigue strength. Only a small fraction of the publication shows the results of fatigue investigations on specimens in as-brazed conditions [8, 14] in which the macro-geometrical shape of the fillet is addressed in addition to the abovementioned influences on the fatigue strength.

In none of these publication, information, on assessment approaches have been given. Only in a few contributions [10,11,12] approaches to numerically asses the fatigue strength of brazed components are described. The main focus of the investigations was the influence of defects. Based on these defects, crack propagation analyses were performed to assess the fatigue life.

This short literature overview shows the current state of the art concerning the fatigue assessment of brazed joints. With reference to the abovementioned brazed joints in rails, the described assessment approach is not applicable. Time-consuming fracture mechanical analyses cannot be performed in industrial practice.

In order to fill this gap, investigations on brazed specimens and specimen-like components are performed. These investigations and approaches to assess the fatigue strength are presented in the following.

2 Manufacturing and characterization of the test specimens

2.1 Specimen geometry and manufacturing

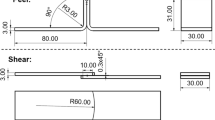
The focus of the study is the structural durability of brazed joints of rails for direct fuel injection. Based on analyses of the macroscopic dimensions and the microstructure as well as the typical fracture characteristics of these brazed joints [6], shear and peel test samples were derived (Fig. 1a, b) [5]. Additionally, a more complex component-like specimen with a T-shape made of two pipes was developed based on the actual geometry of the application-relevant rails (Fig. 1c).

Fig. 1
figure 1

Geometry and loading mode of the derived test specimens: a shear specimen, b peel specimen, c component-like specimen

Full size image

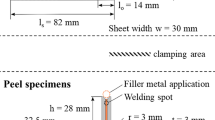
The steel plates as well as the pipe segments were made of 1.4301 (X5CrNi18-10, AISI 304). The plates had a thickness of t = 3 mm. For the peel specimens, they were bent to an angle of α = 90∘. Prior to brazing, the parts of the peel and shear test sample were fixed by spot welding, thus creating a joint gap of around d = 80 μ m. The base pipe of the component-like specimens (Fig. 1) had a length of lbase = 110 mm, an external diameter of dbase = 18.6 mm in the testing area, and a wall thickness of tbase = 2.1 mm. The upper pipe segment had a length of lup = 35 mm, a diameter of dup = 16 mm, and a wall thickness of tup = 6 mm. The upper part of the component-like specimen was also fixed by four weld spots to the base pipe.

Prior to brazing, the samples were ultrasonically cleaned with the cleaning agent Galvex Su 93, followed by rinsing with deionized water. Cu 110 according to DIN EN ISO 17672 was used as filler metal. A defined, but sample-specific amount of the brazing paste INNOBRAZE 100/NC was applied on one side of the brazing gap. A brazing temperature of Tbraz = 1120 ∘C was reached for \(t_{\text {braz}}=2~\min \limits \) during the brazing process in a continuous conveyer belt furnace in a hydrogen atmosphere, with a dew point of approx. \(T_{\text {dew};H_{2}}=-~40~^{\circ }\)C. The component-like specimens were brazed lying on one side in order to produce two different kinds of fillet geometries.

2.2 Characterization

After brazing, the sample characteristics and quality was analyzed with different methods to evaluate the influencing factors of the joint geometry on the fatigue behavior. More than 20 test specimens have been characterized metallographically showing comparable microstructures. Additionally, all samples were ultrasonically tested with the immersion technique, and the geometry of the fillet was determined by analyzing the imprints of the joints. Thus, the quality of the brazed joints can be monitored. Furthermore, characteristics such as the fillet radius and topology are documented to be correlated with the fatigue behavior.

2.2.1 Microsections

For all specimen types, the microstructure, surface topology, and inner structure was determined in the cross-section. After etching the cross-sections of the brazed shear specimen, a difference in the surface topology of the fillets in dependence of the position on the sample can be observed (Fig. 2). At the position where the Cu paste was applied before brazing, the surface is smoother due to finer grains. On the opposite side, where the molten filler flows from the brazing gap, the grains are bigger and shrinkage voids have formed between the grains during solidification.

Fig. 2
figure 2

Etched cross-sections of a brazed fillet in the middle of a shear specimen; (left) position of the paste application and (right) opposite side

Full size image

The topology of the fillet of the peel specimen is comparable to the fillet surface at the opposite side of the shear specimen (Fig. 3). The rough structure is likewise a result from the growth of big Cu grains in the fillet. In contrast to shear specimen, the fillet has a more defined radius due to the geometry of the joint gap.

Fig. 3
figure 3

Cross-section of the fillet of the peel test sample in the middle of the specimen

Full size image

At the component-like specimens, the brazing paste was applied on top of the lying sample, leading to a defined fillet geometry after brazing (Fig. 4). Driven by gravity, the molten filler metal flowed through the brazing gap and formed a broad fillet opposite at the lower sample position (Fig. 4b).

Fig. 4
figure 4

Brazed component-like specimens and cross-sections of the a paste application and b opposite side

Full size image

2.2.2 Fillet radii

For a geometrical documentation of the fillet radii, imprints of the joints were produced with a silicon-based impression material. The imprints were cut into slices and analyzed with a microscope to measure the radius of the fillet that were assumed to have a strong influence on the fatigue strength (Fig. 5). On the peel specimens, the fillet radius rp varies between 259 and 1622 μ m with a median of 829 μ m. The fillet radius rs, a on the application side of the filler metal varies between 529 and 1750 μ m with a median of 1597 μ m on the shear specimens. The opposite side has a filler radius rs, o of 259 μ m and 1794 μ m with a median of 1330 μ m. The component-like specimen has three relevant radii. The radius on the application side rd, a varies between 583 and 5552 μ m with a median of 808 μ m. On the opposite side, the radius rd, o ranges from 507 to 6826 μ m with a median of 2983 μ m. The comparatively large scatter and values on the opposite side result from both the difficulties to fit a radius to the undefined surface topology and the high amount of copper due to the relative position in the furnace. The fillet radii on both sides are subsumed in the value rd, s. This radius varies in a range of 552 μ m ≤ rd, s ≤ 1656 μ m with a median of 1042 μ m.

Fig. 5
figure 5

Box plots of the fillet radii (r) of the peel (p), shear (s) specimens, and the component (d) for the application side (a), the opposite side (o), and the crown of the tube–tube connection (s)

Full size image

2.2.3 Ultrasonic testing

With ultrasonic testing, it is possible to analyze the entire joint area to obtain an overview of the joining quality. Here, a focused ultrasonic probe with a frequency of f = 15 MHz was applied and achieved an accuracy of 0.3 mm for each pixel. The immersion technique was used to produce images of the reflection behavior. The C-scan visualizes the amplitude of the acoustic reflection at the interface of the brazed joint (Fig. 6). A low amplitude (gray color) stands for a good bonding, while white areas with a high amplitude imply defects such as voids. Due to the nature of ultrasonic testing, i.e., the measurements of reflections of the ultrasonic waves, only information on voids in the main cross-section of the specimen could be gathered. No information on the void directly present in the fillet radii could be obtained.

Fig. 6
figure 6

Exemplary results of the brazed joints by ultrasonic testing in immersion technique for a peel specimen (a), a shear specimen (b), and component (c). The scans prove a dense structure of the brazed joints

Full size image

All three specimen types showed a dense bonding in the main cross-section. Only some small voids have been detected, which had no influence on the fatigue life in subsequent fatigue tests.

3 Fatigue testing

3.1 Test conditions

Fatigue tests were conducted on the specimens described above in the as-brazed condition using load control (Table 1). Depending on the load level and the specimen type, test frequencies in a range of 10 Hz ≤ f ≤ 35 Hz were used. The shear and peel specimen were tested under axial loading using an R-ratio (\(R=F_{\min \limits }/F_{\max \limits }\)) of R = 0 and = 0.5. The free length (distance between clamps) was lf = 65 mm for both specimens. Three different load configurations were used for the component-like specimen: first, a load (R = 0 and R = 0.5) on the upper pipe in direction of the base pipe, referred to as “in-plane bending” in the following. Second, a load (R = 0) on the upper pipe was applied in direction perpendicular to a surface, generated by the upper and base pipe (“out-of-plane bending”). Third, pressure loading was used with a minimum pressure of \(p_{\min \limits }=50~\text {bar}\).

Table 1 Overview on the fatigue test results for constant amplitude tests and variable amplitude tests (VA)
Full size table

The failure criterion of the demonstrator under pressure loading was leakage of the pressure medium. All other tests were stopped at a defined stiffness loss. This corresponds approximately with a complete fracture of the joint. For these failure criteria overall, ten S-N curves were derived.

3.2 Shear and peel specimens

At the peel specimens, cracks initiated in the fillet of the brazement during testing. The crack propagation occurred solely in the braze so that both sheets were separated after the tests. The failure criterion “fracture” was chosen for the statistical evaluation [21]. Only tests with a maximum load of \(F_{\max \limits }=4~\text {kN}\) were considered in the evaluation (Fig. 7). At higher loads, yielding occurs in the cross-section of the base metal, which leads to a change in the overall specimen geometry and subsequently to a decrease in local stresses. The tests on the peel specimen show a scatter band of TS = 1 : 1.19 for R = 0 and TS = 1 : 1.27 for R = 0.5. The slope of the S-N curve was determined to k = 5.0 for R = 0. Since the fatigue tests at R = 0.5 are within a cycle-range of less than a factor of 10, this slope was taken as given for the statistical evaluation. Even though the tests were conducted up to N = 1 × 107 cycles, no information on the knee point could be identified. A mean stress sensitivity M [17] of

$$ M=\frac{F_{a}(R=0)-F_{a}(R=0.5)}{F_{m}(R=0.5)-F_{m}(R=0)}=0.08 $$
(1)

was determined using the fatigue strength in the high cycle fatigue regime from the tests.

Fig. 7
figure 7

S-N curve for the peel specimen

Full size image

The cracks initiated in the fillet of the braze during the fatigue tests of the shear specimens. Looking at the cross-section at this point (Fig. 2), the distance of the crack initiation position and the base material was approximately 0.2 mm. Consequently, the crack propagated first through the braze and then through the base material during the tests. For the evaluation, only tests with a maximum load of \(F_{\max \limits }=10~\text {kN}\) were considered (Fig. 8). As already described for the peel specimen, yielding leads to a change in the geometry, and thus to an under-proportional increase in stresses in the braze. The statistical evaluation results in a very small scatter band of TS = 1 : 1.05 for R = 0 and TS = 1 : 1.11 for R = 0.5. The slope was determined as k = 6.6. As for the peel specimens, no information on the position of the knee point can be derived from the test data. A mean stress sensitivity of M = 0.16 was determined in the high cycle fatigue regime.

Fig. 8
figure 8

S-N curve for the shear specimen

Full size image

3.3 Component-like specimens

For the component-like specimens with in-plane bending a S-N curve with a slope of k = 5.8 and a low scatter of TS = 1 : 1.09 was evaluated based on the test data (Fig. 9). The endurable load amplitude at N = 107 load cycles resulted in Fa = 450 N for the R-ratio of R = 0. With few tests at higher mean loads (R = 0.5), the endurable load amplitude was estimated as Fa = 345 N. The slope and the scatter were adapted from the tests at R = 0. From both test series, a mean stress sensitivity of M = 0.18 was derived. As for the peel and shear specimens, no indication of a knee point could be identified.

During fatigue testing, cracks initiated in the fillet of the braze. In most cases, the cracks grew in the base metal of the base tube. Only in a few cases at R = 0 and at predominantly higher loads did the cracks grow along the bonding surface.

Fig. 9
figure 9

S-N curve for the component-like specimens with in-plane bending

Full size image

For the component-like specimens with out-of-plane bending, a S-N curve with a slope of k = 5.5 was evaluated (Fig. 10). The endurable load amplitude at N = 107 load cycles resulted in Fa = 318 N for the R-ratio of R = 0. In comparison to the tests with in-plane bending, the scatter of TS = 1 : 1.19 is slightly higher.

Fig. 10
figure 10

S-N curve for the component-like specimens with out-of-plane bending and pressure loading

Full size image

The fatigue cracks start from the fillet of the brazement and propagate along the braze. At the end of the test, both tubes were separated.

The fatigue tests on the component-like specimens with pressure loading revealed the most shallow S-N curve with k = 9.31 (Fig. 10). The endurable pressure amplitude is determined with pa = 275 bar at N = 107 load cycles. The scatter results in TS = 1 : 1.20.

During fatigue testing with pressure loading, the failure starts from the fillet of the brazement and propagates through the base metal of the base tube. The tests are stopped when a leakage of the pressure medium was detected. The location of the cracks varied randomly between the application side and the opposite side; see Fig. 4 and the different markers in Fig. 10.

An overview on the main features of all derived S-N curves is given in Table 1.

3.4 Variable amplitude loading

The majority of components are loaded in service not only by constant but by variable amplitudes. Subsequently, fatigue tests have been conducted using the load sequence “CORAL” (Fig. 11) [23]. The acronym CORAL stand in short for COmmon-RAil-Load. CORAL has a sequence length of LS = 30.000 load cycles. Remarkable in the sequence are the start and stop cycles in which the load is reduced to null resp. to 16% of the maximum load. These can very well be identified in the rainflow matrix due to their high number of occurrences. In the load spectrum, additionally many cycles with a low amplitude and high mean stress are included that represent the pressure changes for each injection process. For a damage accumulation of this load sequence, the information on the mean stress sensitivity is of high relevance. This was the reason for performing constant amplitude tests at R = 0.5.

Fig. 11
figure 11

First 1000 load cycles, rainflow matrix, and damage matrix of the load sequence CORAL

Full size image

In order to analyze the load sequence CORAL, a linear damage accumulation according to Miner with a slope of \(k^{\prime }=k\) following the knee point was conducted. The damage of each cell in the rainflow matrix was accumulated and plotted again as matrix (Fig. 11). For this, the slope of the S-N curve of the shear specimens (k = 6.6) was used. As it can be seen in the damage matrix, both cells show that the start-stop cycles are most damaging. In this case, the accumulated damage reaches approximately 80% of the total damage.

Variable amplitude fatigue tests with the load sequence CORAL have been conducted on the shear specimen and the component-like specimen up to N = 2 × 107 cycles. In order to identify the characteristic damage sums DC, a linear damage accumulation according to Miner was performed. The basis for the damage accumulation was the S-N curve under constant amplitude loading. The Miner rule with a slope \(k^{\prime }=2\times k-1\) following the knee point as proposed by Haibach and a knee point at Nk = 1 × 107 load cycles was applied. The resulting Gaßner curves show a similar slope as the S-N curves (Figs. 8 and 9).

The characteristic damage sums DC are identified by taking the ratio between the numerically derived cycles to failure Nf,num using linear damage accumulation and the experimentally identified cycles to failure \(N_{f,\exp }\). A characteristic damage sum of DC = 0.2 is derived for the shear specimens and DC = 0.4 for the component-like specimens with in-plane loading. A statistical analysis of all damage sums leads to a mean value of DC = 0.3.

3.5 Damage behavior

As already indicated above, the fatigue cracks always started at the fillet of the braze. This was evaluated based on photographs of the fillet during fatigue testing. The crack initiation did start early during the tests for some specimens. Especially at the peel specimens, first cracks could be observed at approx. 15% of the total lifetime (Fig. 12). An evaluation of the photos in order to achieve a quantification in terms of crack length and crack depth was quite challenging due to the roughness of the surface. The roughness results from the dendrites forming during the solidification of the filler metal. At the contact areas of the dendrites, crack-like features are visible that reach deep into the braze material. These voids could be identified for all specimens and are also visible in some cross-sections (Figs. 2 and 3). Due to these conditions, an unambiguous identification of the crack initiation can only be achieved if a crack propagates through a dendrite as it can be seen in Fig. 12 or if the crack-like feature widens significantly. But in any case, a reliable correlation between crack length and number of cycles cannot be derived.

Fig. 12
figure 12

Formation of cracks during the fatigue test at a peel specimen

Full size image

Nevertheless, the visually determined cycles to crack initiation as well as the cycles at a 5% stiffness drop of the specimen were evaluated (Fig. 13). In this evaluation, the peel specimen showed the earliest crack initiation of all specimens. In contrast, a comparatively short remaining lifetime could be identified at the shear specimen, as soon as a crack initiation was detected.

Fig. 13
figure 13

Relationship between crack initiation and total lifetime in dependence on the endured cycles to failure

Full size image

A further fractographic investigation revealed some interesting results. A view on the fillet of a peel specimen that was stopped at an advanced crack propagation state shows the dendritic grain structure and the fatigue crack (Fig. 14). The cracks did not start at the location of the maximum stress, in the center of the fillet, but on the boundary between the fine grains close to the surface of the base material and larger grains in the center of the fillet. This crack initiation position is caused by larger voids in the transition area from larger to finer grains.

Fig. 14
figure 14

Scanning electron microscope image of a fillet of a peel specimen after fatigue tests

Full size image

4 Fatigue assessment

4.1 Correlation with the fillet radius

In theory, the fatigue strength of a notched component should decrease with a decreasing radius of the fillet. The basis of this assumption is the increasing stress concentration, resp. the increasing local stresses, with decreasing a radius. A verification of this assumption can be visualized by including an additional marker information in the S-N curves. In Figs. 7, 8, 9, and 10, the color of the background of these markers is chosen to represent the measured fillet radii (see Section 2.2.2). In these graphs, no correlation can be identified to support this assumption. No significant influence of the fillet radii on the fatigue strength can be observed.

For further investigations finite-element models of the different specimens are set up in order to achieve more quantified information on the influence of the radii and, in a last step, to derive reliable fatigue assessment approaches.

4.2 Finite-element models

In order to derive the local stresses for a fatigue assessment, finite-element analyses were performed for both peel and shear specimen, as well as for the component-like specimens (Fig. 15).

Fig. 15
figure 15

Finite-element models for all specimens

Full size image

To account for the dimensional variation of the specimens, individual finite-element models were set up for each peel and each shear specimen. For this, the measured global geometry in terms of the angular misalignment as well as the local geometry in terms of the fillet radii and the bending radii for the peel specimen were considered based on measurements from the quality inspection. In addition, the boundary conditions were adjusted to represent the finite stiffness of the test rigs. The finite-element models were validated by data from an experimental strain analysis. The simulation itself consisted of several load steps. First, the specimens were clamped to derive clamping stresses; second, the minimum load was applied, followed by the maximum load. These simulation steps allowed to derive local stress amplitudes, local mean stresses, as well as stress gradients at the location of maximum stress.

Due to the complex geometry of the braze, the finite-element models of the component-like specimens were generated based on 3D laser scans of two specimens. Two specimens were chosen for the scan which showed a mean value in terms of the measured radii. In contrast to the peel and shear specimens, the clamping of the component-like specimens had not be included in the FE model since no stresses were induced.

In all FE models, linear-elastic material properties as mean values of data found in literature have been used (Table 2). The braze was modeled using a separate volume with the dimensions taken from the metallographic investigations. The material properties for copper have been assigned to that volume. An isometric mesh, based on quadrilateral or hexahedral elements with a quadratic shape function, was used in order to derive trustworthy notch stresses [1]. For the component-like specimens, tetrahedral elements were chosen. The element length at the location of maximum stress was smaller than 0.05mm for all models. Overall, a linear-elastic material behavior was assumed. Non-linearities due to a change of the geometry due to the load were considered.

Table 2 Linear-elastic material data used in the finite-element model
Full size table

4.3 Endurable notch stresses

No approaches are described in the literature how the durability of a cyclically loaded brazed connection as examined in this investigations can be assessed. Therefore, in a first step, endurable maximum notch stresses σe, vM, according to the v.Mises stress criterion, are used for evaluation. These stresses were taken from the FE models. The endurable load amplitudes from the fatigue tests are transformed to endurable notch stress amplitudes for the evaluation. The mean stresses due to the clamping of the shear and peel specimens were also considered.

All endurable notch stress amplitudes can be compared directly with each other if the influence of mean stresses is concerned (Fig. 16). For this evaluation, only fatigue data with low mean stresses has been used (R ≈ 0). Since it is not feasible to use different mean stress sensitivities for different specimens, a general mean stress sensitivity was determined separately on the peel and shear specimen by variation: For each specimen type, the local mean stresses after clamping were taken as a basis. By a variation of M and a transformation of the test data to R = 0, a minimum scatter of the S-N curve for both R-ratios, R = 0 and R = 0.5, could be achieved using the mean stress sensitivity of M = 0.2. It is larger than the mean stress sensitivities determined from the fatigue tests, since tensile mean stresses have been induced during clamping. In addition, the mean stress sensitivity of M = 0.18 is quite close to the experimental determined one for the component-like specimens under in-plane bending.

Fig. 16
figure 16

Derived endurable notch stresses with r = rreal. Transformed to R = 0 with mean stress sensitivity of M = 0.2

Full size image

The derived reference S-N curve has a slope of k = 6.3 that was evaluated as a weighted mean value of all S-N curves [4]. The endurable notch stress amplitude results in σe, a = 105 MPa. With the determined scatter of TS = 1 : 1.52, a design value (PS = 97.7%) of σe, a = 71 MPa can be determined.

4.4 Endurable effective stresses

Local maximum stresses are typically not used for a fatigue assessment. The reasons for this are stress gradients, which lead to a so-called support effect [3, 18, 25] that increase the endurable notch stresses.

For all specimens, the stress gradient Gσ according to [18], which is also used in the FKM guideline [13], was extracted from the FE results. Due to quite similar notch radii for all specimens (Fig. 5), the variance of the stress gradient is comparatively small. The minimum as well as the maximum value of the gradient are derived for the component-like specimens under pressure loading. It ranges from \(G_{\sigma }=0.47~\text {mm}^{-1}\) at the application side (sharp radius) up to \(G_{\sigma }=2.94~\text {mm}^{-1}\) for the opposite side (large radius). The gradients for all other specimens are within this range.

According to the stress gradient approach [18], support factors n can be derived by evaluating the stress gradient with a factor sg as follows:

$$ n=1+\sqrt{G_{\sigma}+s_{g}}. $$
(2)

With these support factors, effective stresses σeff can be calculated as follows:

$$ \sigma_{\text{eff}}=\frac{1}{n}\times\sigma_{\max} $$
(3)

that can be used for a further fatigue analyses.

The parameter sg can be interpreted as a characteristic fatigue value for the braze material. Since sg is not known, it had to be derived empirically by variation. For this purpose, sg was varied within a technically meaningful range of 0 mm ≤ sg ≤ 0.15 mm, and the scatter of the resulting S-N curve was evaluated (Fig. 17). From this procedure, a minimum scatter could be determined at a value of sg = 0.02 mm.

Fig. 17
figure 17

Influence of the parameter sg on the scatter TS of the reference S-N curve using effective stresses

Full size image

The variation of sg shows an evident minimum in the scatter. Yet, the absolute reduction in scatter from TS = 1 : 1.52 to TS = 1 : 1.51 is below 1%. By evaluating the differences in local stresses between the application side and the opposite side of the component-like specimen under pressure loading the scatter could be reduced (Fig. 18). But there are still significant differences in the endurable effective stresses between the test series.

Fig. 18
figure 18

Derived endurable effective stresses with r = rreal. Transformed to R = 0 with a mean stress sensitivity of M = 0.2

Full size image

5 Discussion

In the fatigue tests, a mean stress sensitivity of M = 0.08, M = 0.16, and M = 0.18 could be determined for the peel, shear, and component-like specimens respectively. The mean stress sensitivity itself is a characteristic value. It is influenced by individual properties of the specimen and cannot be directly transferred from one specimen to another. The comparatively low mean stress sensitivity of the peel specimen can, for example, be explained by the angular misalignment that lead to tensile mean stresses in the notch during clamping and, therefore, a higher local mean stress. This may explain the different values between specimen types. In the evaluation of the endurable local notch stresses, a mean stress sensitivity of M = 0.2 was identified, which can be generally used for a fatigue strength assessment. This value does not consider production-related local mean or residual stresses, resulting for example from an assembly of components. These stresses have to be included separately.

A linear damage accumulation of variable amplitude tests with the load spectrum CORAL lead to characteristic damage sums with a mean value of DC = 0.3. In theory, failure should occur at a theoretical damage sum of Dth = 1, but typically lower values are derived [20]. Analysis of the load spectrum CORAL showed that the main damage (≈ 80%) results from the start–stop cycles with a high amplitude. Probably the damage content of the many cycles with a low amplitude but high mean stress is underestimated by the linear damage accumulation. Nevertheless, with DC = 0.3, a damage sum is available for assessing the lifetime of a brazed component. Further tests, also with different load spectra, need to be performed to achieve a statistical coverage.

In the shown evaluations, local approaches were considered in order to achieve a reliable fatigue assessment for brazed components. A reliable fatigue assessment is possible by using maximum notch stresses derived at realistic fillet radii and disregarding support effects from the stress gradients. The notch stress approach utilizes linear-elastic stresses. This means a mean slope k and fixed knee point Nk of the S-N curve has to be given for the application. In the evaluations, an average slope of k = 6.3 was derived. For all specimens, the position of the knee point could not be identified. It might be assumed to be at N ≥ 107 cycles. As characteristic design value, the notch stress amplitude of σe, a = 71 MPa (PS = 97.7%, R = 0) can be used for an assessment.

The overall scatter of the reference S-N curve of TS = 1 : 1.52 might be interpreted as high. Yet, compared to the scatter of welded joints [4] of TS = 1 : 2.06, it is still reasonable, even when considering the broader database with larger sheet thicknesses and material variations in the mentioned publication.

For a further reduction of the scatter and a subsequent increase in the reliability of the assessment, the stress gradients were considered. However, in these analyses, no significant influence of the stress gradients could be observed. Only a marginal reduction in the overall scatter was achieved. Subsequently, further parameters and effects which have a strong influence on the fatigue strength have to be present.

As mentioned in Section 3.5, the evaluation of the fatigue tests was performed based on data for the failure criteria of total fracture. In principle, only cycles to crack initiation can be assessed with linear-elastic approaches [2]. Even though quite some effort was made in order to detect crack initiation cycles, no number of cycles for a specific crack length or depth could be derived. Furthermore, for the component-like specimen under pressure loading no crack initiation was recorded. This prevents a meaningful evaluation. Nevertheless, by looking at the available data from the peel and the shear specimens—long crack propagation phase at the peel specimen, short phase at the shear specimens—the difference in endurable notch and effective stresses would increase (see Figs. 16 and 18).

A further parameter which might influence the fatigue strength is the surface topology and the structural heterogeneities in the fillet of the braze. As described in Section 3.5, the crack seemed to start from crack-like notches in the surface topology, which were formed by the solidification structure of the braze. Especially for the peel specimen, inner irregularities were detected that might lead to a significant decrease in fatigue strength. The presence of some initial cracks might also be supported by the short crack initiation and long crack propagation phase for that specimen. For a better understanding and a quantification of the influence of the quality on the fatigue life of the braze, further investigations need to be performed, ideally on one specimen type with different braze conditions resp. qualities.

Comparing the crack propagation path of all specimens, a further influencing parameter might be identified: In the peel specimens and the component-like specimens under out-of-plane bending, the crack grows solely through the braze material. In the shear specimens and component-like specimens under pressure loading, the crack grows, starting from the fillet of the braze, through the base materials. Up to now it is unknown, if a change in the material properties has some influence on the crack initiation (the distance between the fillet of the braze and the base material is quite small, therefore the crack initiation might be influenced) or on the crack growth phase.

The list of various parameters reveals that there are still some unresolved questions concerning their quantitative influence on the fatigue strength. Nevertheless, a good and reliable assessment can be achieved with the proposed assessment procedure. At the moment, some limitations of the procedure exist which are connected to the data base of the fatigue tests. These are the stress gradients which should be similar to the ones determined at the specimens and, of course, the material combination that probably has a strong influence, as well.

6 Conclusions and outlook

Following main conclusions can be drawn from the presented investigations:

  • A linear-elastic approach based on realistic radii and maximum notch stresses was evaluated in order to assess the fatigue strength of brazed joints. The proposed reference S-N curve with an endurable stress amplitude of σe, a, vM = 71 MPa at N = 2 ⋅ 106 load cycles (for R = 0 and PS = 97.7%) and a slope of k = 6.3 shows a fair scatter of TS = 1 : 1.52 and leads subsequently to a reliable assessment.

  • A negligible influence of the stress gradients at the fillet of the braze was observed. Even by considering support effects due to these stress gradients, the scatter could only be reduced by less than 1%. Subsequently, the assessment quality could not be significantly improved.

  • From fatigue tests with R-ratios between R = 0 and R = 0.5, a mean stress sensitivity of M = 0.2 was determined. This should be included in the assessment.

  • As a characteristic damage sum, DC = 0.3 should be applied when assessing variable amplitude loading.

The remaining scatter of the reference S-N curve is caused by different influences which cannot be clearly quantified and separated up to now. First, the quality of the braze in terms of the surface condition and the inner inhomogeneities seems to have a strong influence on the fatigue life. These effects cannot be captured by using notch stresses derived at an geometrically ideal radius. Additionally, the loading in correlation to the crack propagation direction in scrutiny to the crack initiation position might have an influence on the endurable notch stresses. Further work needs to be done to completely understand these influences in order to increase the assessment reliability.