1 Introduction

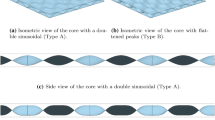
Laser-welded all-steel sandwich panels have shown great promise as load-bearing structural elements. Their high stiffness-to-weight ratio yields a low material consumption compared to conventional solutions. As the efficiency of commercial laser welding sources and the knowledge about laser-based welding is increasing (see research projects HYBLAS [1], FOSTA P869, referred to in, e.g., Peters et al. [2], VAMP27 [3], and Fibertube Advanced [4]), laser stake welds of thicker plates (e.g., 16 mm by using pure laser, Frank et al. [5]) have become possible. This has opened for new possibilities for using laser-welded steel sandwich panels in bridge applications. In this field, the corrugated core steel sandwich panel (CCSSP) (see Fig. 1a) has shown great potential to become a competitive type of steel bridge deck (see, e.g., Beneus and Koc [6], Nilsson and Al-Emrani [7], and Caccese and Yorulmaz [8]). Compared with steel cores with other configurations, the corrugated core gives a higher transverse shear stiffness in the direction perpendicular to the corrugation (see, e.g., Cheng et al. [9]). The high transverse shear stiffness is very favorable in producing a more pronounced “plate action” with an increased two-way load-carrying action which is beneficial for several bridge deck applications. Bridges are subjected to a high number of load cycles during their service life and fatigue is most often the governing limit in the design of steel bridges. In bridges with steel deck, the deck is usually the most fatigue-sensitive part of the bridge as a result of high local stresses due to direct wheel contact.

Fig. 1
figure 1

Laser-welded sandwich specimens with steel S355; a panel (panel B); b beams (beam 1)

Full size image

Steel sandwich panels can be produced with laser or hybrid laser-arc welding. The welding process is fully atomized and performed at a high speed. When performing a stake weld that joins two parallel plates, the laser melts the material in the top plate and also gives penetration into the bottom plate, thus no edge preparation is needed. In previous works, laser welding was utilized in the production of I-core (e.g., Klostermann [10] and Romanoff [11]) and corrugated core (e.g., Peters et al. [2] and Caccese and Yorulmaz [8]) sandwich panels. For CCSSPs, Nilsson et al. [7, 12] showed that dual weld lines are needed to ensure a sufficient service life with respect to fatigue. Several aspects of production of laser-welded all-steel sandwich panels affect the final geometric properties of the panel: both the local geometry of the welded joint and the global geometry, i.e., welding distortions. Examples of production aspects that affect the final panel geometry are as follows: clamping conditions, welding speed, laser power, steel quality, accuracy in actual weld position, etc. The nature of welding production induces a variation of the geometric properties of the joint. Figure 2 shows the production-dependent geometric properties of a CCSSP joint. For CCSSPs, as well as for several other all-steel sandwich panels, the production-dependent geometric properties in the welded joint region are the weld width, tw, weld misalignment, ew, and gap between the core and the face plate, hg. Control of the effect of the spread of the geometric properties is essential in order to ensure sufficient load-bearing capacity throughout the lifetime of the panel.

Fig. 2
figure 2

Production-dependent geometric properties of a CCSSP joint with dual weld lines

Full size image

In previous studies on the impact of production-dependent geometric parameters, the main focus has been on web-core sandwich panels. Frank et al. [5] studied the effect of production-induced variation of geometry in the weld region with respect to fatigue of web-core sandwich panels, loaded in pure tension, by numerical analysis and experiments. The results indicated that a decrease of the ratio of weld width to web thickness yields a decreased inclination of the S-N curve. Romanoff et al. [13, 14] studied the impact of a varying weld region geometry with respect to local and global stiffness. Peters et al. [2] studied the fatigue strength of laser-welded t-joints of web-core sandwich panels including the effect of plate gaps and multi-axial stresses by experiments and numerical analysis. However, the welded joint of a CCSSP preferably has dual weld lines whereas the web-core sandwich panel can only consist of a single weld line. For this reason, a cross section the welds of a web-core sandwich panel is predominantly loaded in bending while the CCSSP weld is in general loaded by a combination of bending and axial force. Figure 3 indicates a section of a laser stake weld. Shear force parallel and perpendicular to the weld line exists in all laser-welded sandwich panels. Furthermore, the welded joint of web-core and corrugated core sandwich panels behaves in principally different way due to the fact that in CCSSPs, the core and the face plates are parallel (at the location of welding), whereas for web-core sandwich panels, they are perpendicular. Thus, contact in CCSSPs takes place with a distance from the weld, while for web-core sandwich panels, contact takes place in the direct vicinity of the weld. Figure 3 shows a comparison of the location of contact between the core plate and the faces for web-core and corrugated core steel sandwich panels. Contact also occurs with a distance to the weld in c-core and z-core sandwich panels. Lok and Cheng [15] derived the weak direction shear stiffness for c-core sandwich panels incorporating linear contact conditions. However, no investigations of the impact of contact on the weld stress were made. For web-core sandwich panels, several authors reported that contact plays an important role with respect to the state of stress in the weld (see, e.g., [2, 5, 16, 17]). Thus, several authors have reported work attributed to the effect of production-dependent geometric parameters as well as the impact of contact for web-core sandwich panels. However, to the authors’ knowledge, these topics have not been addressed with a specific focus on CCSSPs.

Fig. 3
figure 3

Sectional forces acting on a stake weld and points of contact for corrugated core sandwich panels (left) and web-core sandwich panels (right)

Full size image

The main aim of this paper is to investigate the spread of the production-dependent geometric properties at the joint of CCSSPs and the impact of their variation on fatigue-relevant stresses. For that purpose, four CCSSP specimens, two of duplex stainless steel and two of CMn-based structural steel S355, were manufactured. The manufacturing of the panels was performed within the research project INNODEFAB. The production process is herein described in detail. Measurements of the geometric properties of the welded joint are reported and the impact of their variation on the fatigue-relevant stresses in the joint is determined by extensive parametric studies adopting finite element analysis (FEA). For a CCSSP subjected to out-of-plane loads, bending in both the longitudinal direction of the core and the perpendicular direction (weak direction) will cause stresses in the welds, relevant for the fatigue life of the welded joint. However, in this paper, the investigations are focused on the weak direction of the panel. For that reason is a two-dimensional (2D) sandwich beam studied. The beam is a transverse section of the sandwich panel. In the studied direction, both transverse shear (see Nilsson et al. [12]) and bending (see Diffs and Ro [18]) will affect the state of stress in the weld. Two load cases (LCs) are considered in the parametric study of this paper; locally applied load where the load is applied in the center point between two crests and the boundary conditions prevent global bending, and a LC with pure global load effects.

2 Production of panels

The bridge deck panels investigated in this paper were designed by employing an optimization procedure targeting weight minimization. The panels were assumed to be supported on main and transverse girders so as a continuous 5 × 5 m2 plate is analyzed. Two materials were considered: S355 C-Mn steel and Lean-Duplex steel LDX2101. Two panels for each steel type were selected for detailed analysis and later for production and testing. The cross section of the four panels is shown in Fig. 4 with the values of different geometrical parameters given in Table 1.

Fig. 4
figure 4

Notations for cross-sectional geometric properties of a unit cell [12]

Full size image
Table 1 Material and geometry of manufactured panels
Full size table

Even though the corrugated core—in a real industrial production—is meant to be made by means of pressing large plates (see Fig. 5b), the core of the test specimen was composed by welding together one-wave wide channels which were produced by press-braking, Fig. 5a. This was mainly due to practical reasons and cost efficiency in the research project. Thus, for this project, the upper joints were welded with two stake welds per crest, with pure laser, while the lower intersections were welded with three stake welds where the mid-weld was made with hybrid laser-arc welding and the welds on each side were performed with pure laser, see Fig. 5b.

Fig. 5
figure 5

Two ways of manufacturing the continuous core; a separate channels (continuity is created by hybrid laser-arc); b continuous cold-formed core plate

Full size image

The CCSSPs were manufactured in two steps; first, the channel-shaped core sections were mounted in series with direct contact onto the bottom face plate with fixtures consisting of perpetual I-beams, see Fig. 6. The core sections were welded together, and fusioned into the bottom face plate with stake welds. These stake welds were made by hybrid laser-arc (center weld) and pure laser (on each side of the center weld) welding; see typical cross section in Fig. 7. The second step in the manufacturing of the panels was to mount and fixture the top plate (using I-beams analogous to the fixture of the core channels), followed by sequential pure laser welding with two stake welds per joint.

Fig. 6
figure 6

An illustration of the fixturing of core sections to the bottom face plate—before the first step in welding where three longitudinal welds per intersection are made

Full size image
Fig. 7
figure 7

A typical joint at the bottom face of the panel with three welds; the middle weld performed with hybrid laser-arc and the side welds with pure laser

Full size image

The goals for the welding were to achieve sufficient weld width in the plate intersections core-top and core-bottom face, and also to secure sufficient weld penetration—to ensure that the panel has full strength with respect to static and cyclic loading.

Welding of the first sandwich panels (panels A and B, see Table 1) was made in the following sequence. Starting with the bottom joints, the laser hybrid welds that joined the core sections and fusioned into the face plate were made first followed by the pure laser welds. All welding was performed sequentially mid-left-right-left-right, etc. towards the ends of the panels. This caused, however, deformations in the joint which in turn led to difficulties in performing the last outer-side laser welds. There was also some burn-through of welds in the first produced plate, i.e., the laser beam penetrated both plates. The welding sequence and weld data were therefore changed in the production of the other two panels. For panels C and D, the pure laser welds connecting the core channels to the bottom face were made first—starting at the end (side) welds to keep the core plates in position. In the subsequent step, the laser hybrid welds were made in the lower part of the panel, always distributing the heat: mid weld-then left side-then right side, etc. Finally, the top face plate was mounted and welded with only pure laser welds following the same welding sequence for a uniform heat distribution. This modified welding sequence was successful and resulted in significantly reduced deformations in the bottom face joints and fully acceptable results.

The welding data for both the hybrid laser-arc and the pure laser welding was adjusted to ensure that burn-through of the plates could be avoided—but still to ensure that welds with at least 2 mm weld width and sufficient penetration could be achieved. Table 2 shows all applied welding data used to manufacture the sandwich panels.

Table 3 Final weld data for the panels (H = hybrid, L = pure laser)
Full size table

The welding of the CCSSPs reached through iterative steps fully acceptable results, the goals regarding penetration and weld width were reached. The distortions were managed, and with more work, more improvements are possible. The best results for distortion and form stability were achieved when the pure laser welds were performed first, and the hybrid laser-arc welds last. In particular, the outer-end laser welds should be made first of all, to lock the panel dimensions.

Panel B and C were left in their original shape to be tested and measured as panels. However, testing of the panel specimens is outside of the scope of this paper. Panels A and D were cut in the direction perpendicular to the core into beams, see Fig. 1b. Beams from panels A and D are referred to as beams 1 and 2, respectively. The dimensions of the panels are given in Table 1 with notations according to Fig. 4.

3 Measurements

The measurements of the production-dependent geometric properties of the CCSSP joints are made on both the panel and beam specimens. Weld width and plate gaps are measured on beam-type specimens, whereas weld misalignment and initial distortion are measured on the panels.

3.1 Weld width

Measurements of the weld width are executed by using an optical microscope. Example of a welded joint, weld width, and plate gap images can be seen in Fig. 8. All joints were prepared by manual disk grinding and gradually finer abrasives. For beam type 1, measurements are carried out at four cross sections, thus at 4 × 8 joints with two welds each. For beam type 2, three cross sections with six cells and two welds per cell were measured. This yields 64 measurements each for welds in the top and bottom faces of beam type 1. The corresponding number of measurements of beam type 2 is 36. Also, 28 and 15 data points of measured hybrid weld widths are collected from beams 1 and 2, respectively. A number of data points have been given the value 0. This is due to either that the weld has not penetrated into the underlying plate (total 3 points) or that the weld was not distinctly defined in the microscopic image (total 9 points). Thus, 12 out of 243 welds were measured to 0. Furthermore, a number of data points with very large widths (5–9 mm) are identified. All of these points are associated with large gaps. For these points, the plate gap is too large to form a typical stake weld shape, see Figs. 7 and 9. There are in total eight measurements of this type. Figure 10 shows measured weld widths, excluding the abovementioned zero and large widths. All data points are given in Table 5 of Appendix A. Figure 10 shows that the vast majority of the weld width data is within the range of 1–4 mm. The mean weld widths are calculated to 2.1 and 2.6 mm for the pure laser welds and hybrid laser-arc welds, respectively.

Fig. 8
figure 8

Picture of dual weld joint detail; a microscope image of gap; b microscope image of weld; c camera image of joint

Full size image
Fig. 9
figure 9

Example of mis-shaped weld

Full size image
Fig. 10
figure 10

Weld width measurements of beams 1 and 2; a top face laser welds (through 8 mm into 6 mm); b bottom face laser welds (through 6 mm into 5 mm); c hybrid laser-arc welds (butt-weld of two 6 mm and penetration into 5 mm plate)

Full size image

3.2 Weld misalignment

The weld misalignment measurements are performed on panels B and C in the top face and at the free ends by using a digital vernier caliper. This gives 16 data points per panel. The distance between the welds in a weld-pair in the top face is fairly exact: 30 mm. Thus, the distance from the center of the weld-pair to the start of the core radius is measured and used to calculate the weld misalignment (see Figs. 2 and 4). All weld misalignment measurements are shown in Fig. 11 and numeric values of all measured points are found in Appendix A, Table 6. Table 6 shows that the weld misalignments at a limited number of points is large, in fact, up to 15 mm, i.e., the weld is located at the end of the horizontal part of the core, f2, see Fig. 4. However, these cases are rare and approximately 70% of the measured misalignments are equal to or below 2 mm.

Fig. 11
figure 11

Measured weld misalignments of panels B and C

Full size image

3.3 Plate gap

As for the weld width, the plate gaps are measured by using digital images from an optical microscope, see Fig. 8. All measured plate gaps are shown in Fig. 12 and are given in numerical form in Table 7 of Appendix A. As can be seen, there is a large scatter in the plate gaps, and as mentioned above, large gaps can induce badly shaped welds, likely also with a small depth of penetration into the underlying plate. At the bottom face of panel C, which was produced with a revised welding sequence, all gaps are measured to zero. When the welds of the bottom face of panel B were made, the mid hybrid weld was executed before the side pure laser welds. For panel C, the situation was reversed. Thus, when separate channels are used and the side laser weld is executed before the mid hybrid weld, initial contact is always observed. The reason for this is due to the ease of clamping a single channel.

Fig. 12
figure 12

Measured plate gaps for joints at: a top face; b bottom face

Full size image

3.4 Welding distortion

In order to quantify the distortions due to welding, 3D scanning of the top and bottom surfaces is conducted. The result at the mid-section of panels B and C (x = 1000 mm, see Fig. 13) is shown in Fig. 14. The maximum deformation of panels B and C is approximately 8 and 13 mm, respectively. The reason for the larger distortion in panel C can be related to both the thicker top face and the higher thermal elongation of the stainless steel. Seen on the whole width of the panels, the deformation is in the negative z-direction, thus lifting of the free edges. However, locally, between the welded joints, the deformation is positive. The positive local deformation is due to the side of welding. The welds were made in the negative z-direction and the side with the largest value of z was the side to cool down last, yielding the local deformations in positive z-direction. The global deformation in the negative z-direction originates from the fact that top face was welded last and the main part of the deformations are from the lift of the cells at the free ends (high and low values of y).

Fig. 13
figure 13

Principle sketch and coordinate system for panel

Full size image
Fig. 14
figure 14

Deformed shape after welding at x = 1000 mm for: a panel B; b panel C. Gray curves indicates measurements of the bottom face while the black curves indicate the top face

Full size image

4 Parametric study

4.1 FE analysis and setup

In order to determine the impact of the variation of the manufacturing-dependent geometric parameters on the fatigue-relevant stresses, the transverse response of a CCSSP is studied by the means of FEA of 2D sandwich beams. For the parametric study, three different beams are investigated: beams 1–3. Beams 1 and 2 have the cross-sectional geometric properties of panels A and D and the difference between them is that beam 2 has a decreased angle of inclination in the core and a decreased number of cells. The decreased core angle gives beam 2 an increased shear stiffness. Beam 3 has an increased angle of inclination of the core and a decreased thickness of the core plate. This gives beam 3 a decreased transverse shear stiffness compared to beam 1. Furthermore, beam 3 has an increased number of cells compared to beam 1. All beam geometries can be seen in Table 3 with notations according to Fig. 3. The depth of all beams is 190 mm. In the longitudinal direction (x of Fig. 13), the relevant stresses can be calculated and studied in a conventional manner. However, for stresses originating from load distribution in the direction perpendicular to the core (y of Fig. 13), the state of stress is more complicated, and for that reason a beam from a section perpendicular to the core direction of a CCSSP is studied.

Table 2 Case study geometry
Full size table

The three beams are analyzed for two LCs. Principle sketches for LC1 and LC2 are shown in Fig. 15. In LC1, the load is applied at the top face two unit cells from one free edge in between two welded joints. Thus, in this LC, there is an effect of the locally applied load and the global action is constrained. LC2 is studied to investigate the impact of the production-dependent parameters during pure global load effects on the panel, where transverse shear is dominant. For LC2, the load is applied 3p in from the maximum value of y. For all analyses of the parametric study, stresses are captured at the joint with its center at y = 5p, see Fig. 15.

Fig. 15
figure 15

Principle sketch of used load cases; a load case 1; b load case 2. Rectangle indicates output position

Full size image

2D FE models with eight-node continuum elements that incorporate second-order shape functions are used for the parametric study. The 2D solid elements are modeled in plane strain conditions. Three stresses from each FEA are extracted, see Fig. 16. These are the normal stress in y-direction in the core and the top face at the location of the weld as well as the largest magnitude of maximum principal stress along the circumference of the notches. Fatigue cracking can start at the weld toe in the top plate or in the core (modes i and ii of Fig. 16). This mode is governed by the normal stresses in the outermost fibers in these two plates. The weld reinforcement width can vary, but for the laser welds analyzed in this paper the width is typically about 4 mm. However, the hybrid laser-arc welds have about 10 mm weld reinforcement width. For evaluating the load effects in the parametric study, a distance of 10 mm is used, i.e., the results are extracted along a distance of 5 mm on each side of the center of the weld. The maximum stress along this distance is used as a measure of fatigue design stress. More critical is fatigue cracking of the welds themselves; see mode iii in Fig. 16. This is evaluated using the Effective Notch Stress method, following the guidelines given by Fricke et al. [19]. The mesh over a unit cell is shown in Fig. 17.

Fig. 16
figure 16

The location of output stresses and corresponding cracking modes of the parametric study

Full size image
Fig. 17
figure 17

Typical FE-mesh for the output cell used in the parametric study (beam 1, tw = 2.5 mm, ew = 0, hg = 100 μm)

Full size image

Each of the parameters tw, ew, and hg are evaluated on three levels: [1.0, 2.5, 4.0 mm], [− 2, 0, 2 mm], and [1, 50, 100 μm] for the three parameters, respectively. All models have each weld defined by two notches of radius 0.05 mm. Thus, for the gap level 100 μm, the notch is of “U-shape” type, whereas for the other gap levels the notches are of the type “keyhole.” For the case of 4 mm core thickness and 1 μm plate gap, the keyhole notch creates a cut-out in the core plate corresponding to 1.25% of the plate thickness. This is the case with the largest amount of disturbance from the keyhole notch cut-out and the effect of it on the studied stress components is negligible. However, using the common 1 mm notch radius would lead to considerable impact of the cut-out. The reason for the constant notch radius is to get comparable notch stresses for varying plate gaps. Thus, this parametric study is limited to maximum plate gaps of 100 μm which covers a large amount of the measured gaps, see Fig. 11. However, larger plate gaps were also measured, and to investigate the effect of these, separate investigations are executed in a following sub-section.

The parametric study is performed in a full factorial manner, yielding 27 FEAs per beam and LC. Furthermore, all models are executed both including and excluding contact interaction between the top face and core plate. This gives a total of 324 FEAs within the parametric study. The contact constraints are in all possible surfaces between the top face and the core and of the type “hard” according to ABAQUS [20]. No friction is considered between the contact surfaces. All runs can be seen in Table 8 of Appendix B.

The contact models are in their nature nonlinear and the state of stress in the structure is load-path dependent. The load level for the parametric study is defined such that it yields a theoretical fatigue life of 2 million cycles. In order to find the appropriate load level for each beam, the case of a 2.5-mm weld width and 0 misalignment is chosen as a reference. For each beam and LC, the three fatigue design stresses (see Fig. 16) are extracted and normalized by their respective fatigue detail category (C-class). For the toe-cracks at the upper surface of the top face and the core bottom surface (see Fig. 16), C-class 100 is chosen in accordance with HYBLAS [1]. For the notch stress, C-class 630 is used in accordance with Fricke [19]. The point where the normalized stress in the reference case reaches a value of unity, i.e., where the fatigue life is 2∙106 cycles, is chosen as the design load level for the respective beam and LC in the parametric study.

Figure 18a–c shows the normalized stress as a function of applied load for the three stress components for beam 1 and LC1. For this beam and LC, the design load level is ~ 6 kN and the notch stress is more critical than the normal stress components. Furthermore, it can be seen that for this model and at the designing load level, the models with 50 μm plate gap or larger shows no effect of contact. In Fig. 18, the load magnitude that causes yielding (in the center point between two crests, under the applied load) is also identified (this is the first point to reach yielding, i.e., 355 MPa Von-Mises stress, except a limited region in the direct vicinity of the weld notch). The load level where yielding is reached is between 18 and 20 kN for the different gap levels, i.e., approximately three times the design load. Concerning fatigue load effects, the main results from all other cases are given in Table 4. From Table 4, it can be seen that the weld notch stress governs the fatigue design in all cases except for the case of beam 1 and LC2. It can also be noted that the design load level for all beams of LC1 follows the top face local span width. Thus, p is in general likely to be an important parameter for the stress magnitude in the weld notches for the local LC1.

Fig. 18
figure 18

Stress normalized by C-class as a function of applied load for beam 1 and LC1, tw = 2.5 mm, and ew = 0 mm; a weld notch principal stress (C 630); b top face normal stress at the weld location (C 100); c core normal stress at the weld location (C 100)

Full size image
Table 4 Design load level for all beams and load cases
Full size table

For the parametric study of this paper, a “one-factor-at-the-time” approach is used. Each parameter has three levels; thus, two changes are possible, denoted as the low and high range. For the plate gap and weld width, the low range is defined as the relative change in stress when going from the low level to the mid-level, and the high range is defined by a change from the mid-level to the high level. For the weld misalignment however, the low range is defined as the change when going from the mid-level 0-value to the low level and the high range is defined by a change from the mid-level 0-value to the high level.

4.2 Results

As mentioned above, the impact of each parameter on the fatigue-relevant stress in each studied location is investigated using the relative change in stress when going from one level to another. As an example, the relative stress change in the low range for the core stresses is calculated by (σc,2 − σc,1)/σc,1 where σc,1 and σc,2 denotes the core stress at the low and mid-level for a specific parameter, respectively.

4.2.1 Top face stresses

Figure 19 shows the relative change in top face stress for all beams, LCs, parameters, and including or excluding contact interaction. Each point in Fig. 19 (and coming equivalent figures for other stress locations) represents the change in stress as a result of changing one of the three investigated parameters, keeping all other parameters (two of the three investigated parameters: LC, beam, and contact condition) constant. With respect to changing weld width in LC1 and LC2 or weld misalignment in LC2, all beams—both in the low and high range—are affected less than 4%, see Fig. 19a, b, d. For the low and high range in LC1, weld misalignment can increase (low range) and decrease (high range) the top face stresses in beam 3 by a maximum of 8%. For beams 1 and 2, the corresponding number is approximately 5%, see Fig. 19c. Thus, weld width and misalignment have in general a modest effect on the top face stresses for the investigated cases.

Fig. 19
figure 19

Relative change in top face stress for beams 1–3; a effect of tw, load case 1; b effect of tw, load case 2; c effect of ew, load case 1; d effect of ew, load case 2; e effect of hg, load case 1; f effect of hg, load case 2; C, contact; NC, no contact; *, low range; **, high range

Full size image

Figure 19e, f shows the impact of changing the plate gap. It is seen that the plate gap has no impact on the stress level in the top face when contact interaction is excluded. However, the plate gap size is the main parameter influencing the contact load level. The low range of Fig. 19e, regarding LC1, shows that when going from a 1-μm to a 50-μm plate gap, the top face stresses increase by up to 50%. Thus, when increasing the plate gap, contact does not occur, and the stresses increase. The reason for the decreased stress in the studied weld region is that when contact occurs, the point of the maximum stress moves from the vicinity of the weld to the contact point, see Fig. 3. For the low range of LC1, beam 2 is significantly more sensitive to a change in plate gap compared to beams 1 and 3. For the high range of LC2 (see Fig. 19e), only a single model of beam 2 (ew = − 2 mm, tw = 1.0 mm) has a stress change that is not zero. However, the change is small indicating that the contact load level and the design load level are almost equal. For LC2, going from 1-μm to a 50-μm plate gap decreases the stresses for all beams, see Fig. 19f. Thus, excluding contact interaction increases the stress for this case. However, the effect is modest.

4.2.2 Notch stresses

Figure 20 shows the relative change in weld notch principal stress for all beams, LCs, parameters, and including or excluding contact interaction. Figure 20a shows that increasing the weld width can both increase and decrease the notch stress. The reason for this can be the fact that increasing the weld width increases the interaction between the core and the face plate (see Nilsson el. al. [21]) which increases the stresses in the weld. However, the section modulus of the weld itself and the loaded area are also increased, leading to decreased normal and shear stresses. Moreover, a beam with a wider weld is less prone to contact occurrence due to the higher rotational stiffness of the weld. For LC1, the maximum effect of increasing the weld width by 1.5 mm is 23%, see beam 3 in Fig. 20a. For beams 1 and 2, the effect of increasing weld width by 1.5 mm is less than 10%. For the low range in LC2, an increased weld width lead to decreased stresses except for beam 3, where negligible increases is observed, see Fig. 20b. However, Fig. 20b shows that for the high range there exist cases where beams 1 and 2 get an increased stress by up to 18% due to a 1.5-mm increase in weld width.

Fig. 20
figure 20

Relative change in notch stress for beams 1–3; a effect of tw, load case 1; b effect of tw, load case 2; c effect of ew, load case 1; d effect of ew, load case 2; e effect of hg, load case 1; f effect of hg, load case 2; C, contact; NC, no contact; *, low range; **, high range

Full size image

Figure 20c, d shows that for both ranges and LCs, there are cases regarding a 2-mm weld misalignment change that increase the notch stress significantly. Stress increases by 20 and 40% are shown for LC1 and LC2, respectively. In order to investigate the effect of misalignment further, beam 1 with a plate gap of 100 μm and a weld width of 2.5 mm loaded according to LC2 is analyzed with a ranging weld misalignment from 0 to − 10 mm with steps of 1 mm. The relative change in notch stress for this model is 18% when the weld misalignment is − 2 mm, see Fig. 20d. Thus, this is not the most sensitive case.

Figure 21a shows the relative change in stress for the four studied notches (notches 1–4, see Fig. 15) for LC1. Both maximum and minimum principal stresses are shown as a function of weld misalignment. For zero misalignments is notch 1, the minimum principal stress is governing, i.e., gives the maximum load effect in any of the notches. However, for weld misalignments − 1 mm or greater, the tensile principal stress component of notch 4 governs, see Fig. 21a. Figure 21a shows that the governing notch stress (notch 4) increase linearly from 21 to 160% when the weld misalignment changes from − 2 to − 10 mm. Independent of which notch that is governing (notch 1 or 4), the position of maximum stress within the respective notch is constant and does not change with misalignment. Furthermore, for this case (beam 1, LC2, tw = 2.5 mm, hg = 100 μm, no contact), a corresponding 2D beam model of a unit cell subjected to pure shear load (see Fig. 4) is studied to give insight to the behavior. The model is executed in accordance with the FEAs for validation of the analytic model in Nilsson et al. [12]. However, in this study a full unit cell is used due to the asymmetry of the welds, compared to the half-cell that was adopted in [12]. In order to account for the rotational rigidity of the weld region, a rotational spring according to Nilsson et al. [21] is included in the numerical analysis. This 2D model is used to calculate nominal stresses from moment, normal force and shear force in the beam elements representing the welds. Figure 21b shows the relative change in nominal maximum normal and average shear stress in the right weld of the beam model for comparisons with notch 4. The inclination of the curve representing the change in maximum nominal normal stress is less than the decisive curve of Fig. 21a. However, the change in average nominal shear stress (i.e., shear force) is highly affected by an increased misalignment, see Fig. 21b. Thus, the shear force is likely to contribute most to the increased principal stress observed in Fig. 21a.

Fig. 21
figure 21

Relative change in stress as a function of weld misalignment for beam 1, tw = 2.5 mm, and hg = 1 μm; a LC1 maximum and minimum principal stress for each notch; b nominal normal and shear stress in the right weld

Full size image

Figure 22 shows the principle forces and deformed shape of a unit cell under pure transverse shear in the case of zero and negative misalignment. The reason for the high nominal shear stresses in the weld is believed to be the result of the high stiffness of the joint. The welds are modeled as rigid beams with a rotational spring and the beam elements of the top face and core between the welds have a high axial and bending stiffness due to their high ratio of thickness to length (see A and B of Fig. 22b). When a unit cell with zero misalignments is subjected to transverse shear force, the welds rotate equally, see Fig. 22a. However, in the misaligned case, the forces acting on the welds give them unequal rotation. Due to their high axial and bending stiffness, the beam parts A and B of Fig. 22b cause restraint to the unequal rotation yielding shear forces in the welds that either contributes or counteracts the externally applied load. Figure 20c, d also shows that weld misalignment has higher impact in LC2 than LC1. This is believed to be an effect of that LC1 is not symmetric with respect to load compared to the shear-dominated LC2.

Fig. 22
figure 22

Principle sketch of deformations in the weld region with: a no misalignment; b negative misalignment

Full size image

Figure 20e shows that in LC1, the plate gap has no effect on the notch stress as long as no contact interaction is considered. However, when contact is included in the model, the plate gap has a large effect on the notch stress in the low range, i.e., going from 1 to 50 μm. The reason for this is that contact interaction decreases the stresses for this LC and does in general not occur at the 50-μm level. For LC2, there are cases where the notch stress is affected by a changing gap size for the cases of excluding contact. Nevertheless, the effect is only 6% for the extreme case (see the high range of Fig. 20f). Furthermore, there are cases in which contact increases the notch stresses in the low range of LC2 by up to 20%. The reason for this is analogous to the effect of the impact of weld misalignment, thus diverging rotations of the welds causing constraint effects in the weld region. The position of contact interaction for LC2 is at the left side of the welds (see the deformed shape in Fig. 22). This contact counteracts the natural rotation of the left weld and increases the difference in weld rotation between the two welds. The largest increasing effect on stresses due to contact is yielded for cases of zero weld misalignment; thus, without contact the weld rotations are close to equal. In the non-contact case, the weld rotations are not perfectly equal as the beam is not in a pure shear-loaded state but the bending moment causes diverging weld rotation to some extent.

4.2.3 Core stresses

Figure 23 shows the relative change in core stress in the weld region for all beams, LCs, parameters, and including or excluding contact interaction. Figure 23a, b shows that the weld width does not have a major effect on the core stresses. In LC1, the effect is maximum approximately 10% for beam 3. For the other beams, the effect is less. In LC2, the change in stress is less than 5% for all cases except for a single case of beam 3. However, the stresses are small in this case.

Fig. 23
figure 23

Relative change in core stress for beams 1–3; a effect of tw, load case 1; b effect of tw, load case 2; c effect of ew, load case 1; d effect of ew, load case 2; e effect of hg, load case 1; f effect of hg, load case 2; C, contact; NC, no contact; *, low range; **, high range

Full size image

Figure 23c, d shows that weld misalignment has an effect on the core stress similar to that on the notch stress in Fig. 19c, d. This effect can be explained with the same constraint effect in the region at and between the welds causing axial force in the core and thus also normal stresses at the core bottom surface. It is also noted from Fig. 23d that contact in general counteracts this effect in LC2.

Figure 23f, e shows that when interaction is excluded, the plate gap has no effect on the core stresses. Furthermore, the low range of Fig. 23f shows that increasing the plate gap in LC1 has an increasing effect on the core stress; thus, the contact interaction that occurs in the 1-μm plate gap cases yield decreased stresses. However, for LC2 and the low range, the contact is shown to increase the stress for some cases. Figure 24 shows a principle sketch of the deformed shape and forces acting in the region. The compressive force in the left weld and the forces in the corrugation leg contribute to the compressive stresses in the inner radius and bottom surface of the horizontal part of the core. The contact force is believed to increase this effect.

Fig. 24
figure 24

Principle sketch of contact force impact on the core stresses for LC2

Full size image

4.3 The effect of large plate gaps

In order to investigate the effect of gaps larger than 100 μm, the model of beam 1 with zero misalignment, 100 μm plate gap, and 2.5 mm weld width is compared to a corresponding model with 600 μm plate gap. The analysis is performed for LC1. A U-shaped notch type is used for both models. The effect on the top face and core stress in the weld region is less than 1%. Thus, the plate gap size is not expected to have any significant effect on the top face or core stress as long as contact does not occur. In order to compare both cases with respect to notch stress, the notch stress is normalized with their respective C-class. For the case of a 50 μm radius, the C-class 630 MPa is again used, and for the case of a 300-μm radius, the C-class 320 MPa is used in accordance with Bruder et al. [22]. The analysis shows that increasing the gap from 100 to 600 μm decreased the normalized notch stress with 23%. However, whether that decrease originates from the increased gap or the calibration of the C-classes is hard to distinguish.

5 Concluding remarks

This paper reports the work and experience from the manufacturing process of four laser-welded CCSSPs of conventional structural steel and duplex stainless steel. The production-dependent geometric properties of the welded joint between the core and faces were quantified. Results from the measurements showed that the weld widths in general were between 1 and 4 mm with a mean value of 2.1 and 2.6 mm for the pure laser welds and hybrid laser-arc welds, respectively. The plate gaps varied between initial contact (zero gap height) to the extreme case of 1.3 mm gap. Regarding the weld misalignments, approximately 70% of the measurements were less than or equal to 2 mm. A weld misalignment of 2 mm is judged to be possible also in a large-scale production situation and the effect of a misalignment of that magnitude was in this paper shown to be significant. Furthermore, the impact of all production-dependent geometric properties of the joint region was investigated with respect to fatigue-relevant stresses in the vicinity of the laser stake welds by parametric studies using 2D solid element FEA. From the parametric study, the following conclusions were deduced, valid for the specific cases investigated in this study:

  • The weld width had a small effect on the top face and core normal stresses in the vicinity of the weld.

  • Increasing the weld width can increase or decrease the notch principal stresses. The reason for this can be that the weld width simultaneously impacts several properties. The maximum increase of the notch stress was 23% when the weld width was increased by 1.5 mm.

  • The weld misalignment had a modest effect on the top face stress.

  • With respect to notch and core stress, the weld misalignment was shown to have a significant effect. For both stresses, the effect is greater in LC2 (isolates global load effects) than LC1 (isolated effect of directly applied load), which is related to the symmetry of loads on a unit cell in LC2 being disturbed by the misalignment. Such symmetry is not found in LC2.

  • When contact interaction between the core and the face plate was excluded in the analysis, the plate gap had no or very modest impact on all investigated output stresses.

  • When contact interaction between the core and the face plate was considered, the plate gap had a significant impact on several of the investigated output stresses. Thus, a change in stress due to a change of plate gap is directly related to contact between the core and faces. For LC1, the effect of contact was shown to always be beneficial. For LC2, contact does not have a significant impact on the top face stresses. However, with respect to core and notch stresses in LC2, contact interaction can in some cases lead to higher stresses.

Only few models in the parametric study showed an effect of contact if the plate gap is equal to 50 μm (thin welds and maximum misalignment in beam 2). Furthermore, no model showed an effect of contact if the plate gap is 100 μm. Thus, the gap size must be modest in order for contact to occur under fatigue design load levels for the investigated cases.

The results of this paper display which manufacturing-dependent parameters are important with respect to different stresses. However, in order to define tolerances for a large-scale manufacturing process, further investigations that involve a significant number of different cross sections, bi-directional bending action of the panels, and experimental validation are needed.