Fracture mechanics-based estimation of fatigue lives of welded joints

Abstract

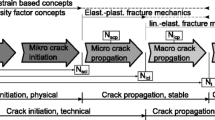
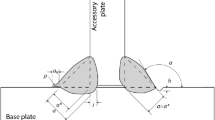
The effects of the lack of penetration flaw and misalignment on fatigue life of cruciform welded joints made of low-alloy steel were studied experimentally and theoretically. It was found that two locations of fatigue fracture were possible under cyclic tension loading, depending on the relative magnitude of the misalignment. In the absence of misalignment, all fatigue failures occurred as a result of fatigue growth of cracks emanating from the weld root. In the presence of misalignment, fatigue life depended on the fatigue growth of cracks growing from the weld toe. It has been shown that the entire fatigue life can be modeled as a fatigue growth of cracks starting either from the weld toe or the weld root. The initial crack size was selected as a small crack characteristic for a given material, i.e., being dependent only on the material. The weight function method was used to calculate the required stress intensity factors.

Appendix

Parameters of the weight function for a semi-elliptical crack in a finite-thickness plate

• For the deepest point O

  $$ \begin{array}{c}\hfill {m}_{\mathrm{O}}\left(x,a\right)=\frac{2F}{\sqrt{2\pi \left(a-x\right)}}\left\{1+{M}_{1\mathrm{O}}{\left(1-\frac{x}{a}\right)}^{\frac{1}{2}}+{M}_{2\mathrm{O}}\left(1-\frac{x}{a}\right)+{M}_{3\mathrm{O}}{\left(1-\frac{x}{a}\right)}^{\frac{3}{2}}\right\}\hfill \\ {}\hfill {M}_{1\mathrm{O}}=\frac{\pi }{\sqrt{2Q}}\left(4{Y}_{\mathrm{o}}-6{Y}_1\right)-\frac{24}{5}\hfill \\ {}\hfill {M}_{2\mathrm{O}}=3\hfill \\ {}\hfill {M}_{3\mathrm{O}}=2\left(\frac{\pi }{\sqrt{2Q}}{Y}_{\mathrm{O}}-{M}_{1\mathrm{O}}-4\right)\hfill \end{array} $$

  where for 0 < a/c < 1:

  $$ \begin{array}{l}Q=1.0+1.464{\left(\frac{a}{c}\right)}^{1.65}\hfill \\ {}{Y}_0={B}_0+{B}_1{\left(\frac{a}{t}\right)}^2+{B}_2{\left(\frac{a}{t}\right)}^4+{B}_3{\left(\frac{a}{t}\right)}^6\hfill \\ {}{B}_0=1.0929+0.2581\left(\frac{a}{c}\right)-0.7703{\left(\frac{a}{c}\right)}^2+0.4394{\left(\frac{a}{c}\right)}^3\hfill \\ {}{B}_1=0.456-3.045\left(\frac{a}{c}\right)+2.007{\left(\frac{a}{c}\right)}^2+\frac{1.0}{0.147+{\left(\frac{a}{c}\right)}^{0.688}}\hfill \\ {}{B}_2=0.995-\frac{1.0}{0.027+\frac{a}{c}}+22.0{\left(1-\frac{a}{c}\right)}^{9.953}\hfill \\ {}{B}_3=-1.459+\frac{1.0}{0.014+\frac{a}{c}}-24.211{\left(1-\frac{a}{c}\right)}^{8.071}\hfill \end{array} $$

  And

  $$ \begin{array}{l}{Y}_1={A}_0+{A}_1{\left(\frac{a}{t}\right)}^2+{A}_2{\left(\frac{a}{t}\right)}^4+{A}_3{\left(\frac{a}{t}\right)}^6\hfill \\ {}{A}_0=0.4537+0.1231\left(\frac{a}{c}\right)-0.7412{\left(\frac{a}{c}\right)}^2+0.4600{\left(\frac{a}{c}\right)}^3\hfill \\ {}{A}_1=-1.652+1.665\left(\frac{a}{c}\right)-0.534{\left(\frac{a}{c}\right)}^2+\frac{1.0}{0.198+{\left(\frac{a}{c}\right)}^{0.846}}\hfill \\ {}{A}_2=3.418-3.126\left(\frac{a}{c}\right)-\frac{1.0}{0.041+\left(\frac{a}{c}\right)}+17.259{\left(1-\frac{a}{c}\right)}^{9.286}\hfill \\ {}{A}_3=-4.228+3.643\left(\frac{a}{c}\right)+\frac{1.0}{0.020+\frac{a}{c}}-21.924{\left(1-\frac{a}{c}\right)}^{9.203}\hfill \end{array} $$

  and for 1 < a/c < 2

  $$ \begin{array}{l}Q=1.0+1.464{\left(\frac{c}{a}\right)}^{1.65}{\left(\frac{a}{c}\right)}^2\hfill \\ {}{Y}_0={B}_0+{B}_1{\left(\frac{a}{t}\right)}^2+{B}_2{\left(\frac{a}{t}\right)}^4\hfill \\ {}{B}_0=1.12-0.09923\left(\frac{a}{c}\right)+0.02954{\left(\frac{a}{c}\right)}^2\hfill \\ {}{B}_1=1.138-1.134\left(\frac{a}{c}\right)+0.3073{\left(\frac{a}{c}\right)}^2\hfill \\ {}{B}_2=-0.9502+0.8832\left(\frac{a}{c}\right)-0.2259{\left(\frac{a}{c}\right)}^2\hfill \\ {}{Y}_1={A}_0+{A}_1{\left(\frac{a}{t}\right)}^2+{A}_2{\left(\frac{a}{t}\right)}^4\hfill \\ {}{A}_0=0.4735-0.2053\left(\frac{a}{c}\right)+0.03662{\left(\frac{a}{c}\right)}^2\hfill \\ {}{A}_1=0.7723-0.7265\left(\frac{a}{c}\right)+0.1837{\left(\frac{a}{c}\right)}^2\hfill \\ {}{A}_2=-0.2006-0.9829\left(\frac{a}{c}\right)+1.237{\left(\frac{a}{c}\right)}^2-0.3554{\left(\frac{a}{c}\right)}^3\hfill \end{array} $$

• For the surface point D

  $$ \begin{array}{c}\hfill {m}_{\mathrm{D}}\left(x,a\right)=\frac{2F}{\sqrt{\pi x}}\left\{1+{M}_{1\mathrm{D}}{\left(\frac{x}{a}\right)}^{\frac{1}{2}}+{M}_{2\mathrm{D}}{\left(\frac{x}{a}\right)}^1+{M}_{3\mathrm{D}}{\left(\frac{x}{a}\right)}^{\frac{3}{2}}\right\}\hfill \\ {}\hfill {M}_{1\mathrm{D}}=\frac{\pi }{\sqrt{4Q}}\left(30{F}_1-18{F}_{\mathrm{o}}\right)-8\hfill \\ {}\hfill {M}_{2\mathrm{D}}=\frac{\pi }{\sqrt{4Q}}\left(60{F}_0-90{F}_1\right)+15\hfill \\ {}\hfill {M}_{3\mathrm{D}}=-\left(1+{M}_{1\mathrm{D}}+{M}_{2\mathrm{D}}\right)\hfill \end{array} $$

  where for 0 < a/c < 1:

  $$ \begin{array}{l}{F}_0=\left[{C}_0+{C}_1{\left(\frac{a}{t}\right)}^2+{C}_2{\left(\frac{a}{t}\right)}^4\right]\sqrt{\frac{a}{c}}\hfill \\ {}{C}_0=1.2972-0.1548\left(\frac{a}{c}\right)-0.0185{\left(\frac{a}{c}\right)}^2\hfill \\ {}{C}_1=1.5083-1.3219\left(\frac{a}{c}\right)+0.5128{\left(\frac{a}{c}\right)}^2\hfill \\ {}{C}_2=-1.101+\frac{0.879}{0.157+\frac{a}{c}}\hfill \end{array} $$

  And

  $$ \begin{array}{l}{F}_1=\left[{D}_0+{D}_1{\left(\frac{a}{t}\right)}^2+{D}_2{\left(\frac{a}{t}\right)}^4\right]\sqrt{\frac{a}{c}}\hfill \\ {}{D}_0=1.2687-1.0642\left(\frac{a}{c}\right)+1.4646{\left(\frac{a}{c}\right)}^2-0.7250{\left(\frac{a}{c}\right)}^3\hfill \\ {}{D}_1=1.1207-1.2289\left(\frac{a}{c}\right)+0.5876{\left(\frac{a}{c}\right)}^2\hfill \\ {}{D}_2=0.190-0.608\left(\frac{a}{c}\right)+\frac{0.199}{0.035+\frac{a}{c}}\hfill \end{array} $$

  and for 1 < a/c < 2

  $$ \begin{array}{l}{F}_0=\left[{C}_0+{C}_1{\left(\frac{a}{t}\right)}^2+{C}_2{\left(\frac{a}{t}\right)}^4\right]\sqrt{\frac{a}{c}}\hfill \\ {}{C}_0=1.34-0.2872\left(\frac{a}{c}\right)+0.0661{\left(\frac{a}{c}\right)}^2\hfill \\ {}{C}_1=1.882-1.7569\left(\frac{a}{c}\right)+0.4423{\left(\frac{a}{c}\right)}^2\hfill \\ {}{C}_2=-0.1493+0.01208\left(\frac{a}{c}\right)+0.02215{\left(\frac{a}{c}\right)}^2\hfill \end{array} $$

  And

  $$ \begin{array}{l}{F}_1=\left[{D}_0+{D}_1{\left(\frac{a}{t}\right)}^2+{D}_2{\left(\frac{a}{t}\right)}^4\right]\sqrt{\frac{a}{c}}\hfill \\ {}{D}_0=1.12-0.2442\left(\frac{a}{c}\right)+0.06708{\left(\frac{a}{c}\right)}^2\hfill \\ {}{D}_1=1.251-1.173\left(\frac{a}{c}\right)+0.2973{\left(\frac{a}{c}\right)}^2\hfill \\ {}{D}_2=0.04706-0.1214\left(\frac{a}{c}\right)+0.04406{\left(\frac{a}{c}\right)}^2\hfill \end{array} $$