Restoration of Noisy Orientation Maps from Electron Backscatter Diffraction Imaging

Abstract

Crystallographic orientations can be measured using scanning electron microscope-based techniques, such as electron backscatter diffraction (EBSD). The orientation data thus obtained may contain noise and misindexed data. There are several methods to restore the orientation data. The restorations from these methods may have varying levels of quality. Moreover, many such methods are parameter-dependent. Therefore, finding suitable parameter settings for optimal restorations can take time and effort for users of such methods. In this paper, we propose an algorithm to obtain high-quality restorations of noisy orientation data and to circumvent the parameter selection problem by automating it. We estimate the noise variance in the data to determine the amount of denoising to apply. We then use this information to determine the stopping criteria for a vector-valued weighted total variation flow, a nonlinear diffusion applied to the noisy orientation map. We compare the results obtained by our approach with the results from other commonly used denoising filters. As benchmarks, we used simulated EBSD maps with varying noise levels. Our proposed method outperformed denoising methods, such as mean, median, spline, half-quadratic, and Kuwahara filters. The denoising results were statistically significantly better for higher levels of noise.

Appendices

Appendix A: The Preprocessing Algorithm

There are two main sources of jump discontinuities in the orientation data: non-unique representations of orientations due to crystal symmetry, and limited range of Euler angle representation. To address the non-unique representation owing to the crystal symmetry, we project the orientations data onto the fundamental region. Note that for each orientation in the data, there is a unique symmetrically equivalent orientation within the fundamental region. In the remainder of the section, we describe the preprocessing algorithm we propose to identify and correct the jump discontinuities due to the range of the Euler angle representation of the data.

The Euler angles range from $0^{\circ }$ to $360^{\circ }$ (or $180^{\circ }$), depending on the axes representation used. For the range [0, 360), the jump discontinuities around angles $0^{\circ }$ and $360^{\circ }$ can cause misorientation errors. As example, consider that an Euler angle is $350^{\circ }$, which due to noise of $15^{\circ }$ changes to $350^{\circ }+15^{\circ }=365^{\circ }$. However, since $365^{\circ }$ is not in the range $[0^{\circ }, 360^{\circ })$, it is recorded as the equivalent angle of $5^{\circ }$ causing a jump discontinuity within a grain, with a large error of $(\, 350^{\circ }-5^{\circ }) = 345^{\circ }$, rather than the original small error of $15^{\circ }$. Fig. 5b shows the jump discontinuities in Euler angles arising from adding $15^{\circ }$ disorientation angle error to data in Fig. 5a. Hence, before applying a denoising algorithm, we need to correct the jump discontinuities at $0^{\circ }$ and $360^{\circ }$ in the data using a preprocessing algorithm. Note that the jump discontinuities are the feature of Euler angles, all images in this Appendix depict normalized Euler angles and are visualized as red, green, and blue (RGB) channels.

Fig. 5

This figure shows the Euler angles in multiple grains of an example EBSD map as an RGB image. Image a shows the ground truth orientations. Image b shows the noisy data with up to $15^{\circ }$ error in Euler angles. The green pixels show the jumps due to the angle discontinuity around $360^\circ -0^\circ$

We demonstrate the steps of this algorithm in Fig. 6. We depict a clean EBSD map example obtained from DREAM.3D software [22, 31] in Fig. 6a. The EBSD maps contain orientations as Euler angles in Bunge notation i.e. ZXZ format [32]. Figure 6b shows the local standard deviations computed in the neighborhood of a $3 \times 3$ window centered at each data point. The brighter spots in Fig. 6b correspond to larger values of the local standard deviations. In Fig. 6c, we see the histogram of the local standard deviations. The orientation values within a single grain of clean EBSD data are comparable, as seen in Fig. 6a. Thus, we expect the local standard deviation near each data point within a single grain to be close to 0. Indeed, this phenomenon is apparent in the histogram of the local standard deviations shown in Fig. 6c. Around 90% of the local standard deviations in Fig. 6c are equal to 0, an effect more pronounced due to the map being synthetically generated.

Figure 6d depicts the EBSD data with de la Vallée Poussin noise [26] with a half-width $b=8$. We compute local standard deviations of the noisy data as shown in Fig. 6 e, with its corresponding histogram in Fig. 6f. Note that Fig. 6e also contains the grain boundaries. The distribution of the local standard deviation is multimodal, with one prominent peak corresponding to the misorientation noise in the EBSD data. The other peaks correspond to the jump discontinuities showing high local standard deviation. To separate the misorientation noise from the jump discontinuities and grain boundaries, we identify the end of the prominent peak. Figure 6g shows the locations with local standard deviations higher than the endpoint of the prominent peak. The Euler angles typically range from $0^{\circ }$ to $360^{\circ }$ (or $180^{\circ }$). If the range is from $0^{\circ }$ to $360^{\circ }$, the two angles are equivalent. In such cases, we only need to identify points corresponding to the jump discontinuities at $0^{\circ }$ and $360^{\circ }$. The jump discontinuities identified by our algorithm are depicted in Fig. 6 g. If the angle $\theta$ at (x, y), a point of discontinuity, is near $0^{\circ }$ (or $360^{\circ }$) while majority of its neighbors are near $360^{\circ }$ (or $0^{\circ }$), we correct the angle $\theta$ to $360-\theta$, otherwise $\theta$ is unchanged. Fig. 6 h shows the EBSD data with the jump discontinuities corrected. The correction of jump discontinuities does not always capture all the discontinuous data points, and the remaining discontinuities may appear as misindexed points. We apply the algorithm given by Brewer and Michael [9] to identify misindexed points. We label a point misindexed if its angle differs from all its local neighbors by $5^{\circ }$ or more. We then replace these misindexed data points with the local median. Figure 6 i depicts the image with the correction of isolated pixels. The circles in Fig. 6 i highlight some regions with these corrections.

Fig. 6

Illustration of processing of noise due to jump discontinuities in the Euler angles: a clean image, b image of local standard deviations, c standard deviation histogram of clean data, d noisy image; the grains with jump discontinuities are highlighted in circles e local standard deviations of noisy data, f standard deviation histogram of noisy data, g region with jump discontinuities, h image with corrected jump discontinuities, i image with corrected isolated pixels. In some regions in h, the isolated pixels were corrected, and the corresponding corrected regions in i are shown in circles

Appendix B: Numerical Scheme

For the weighted TV flow,

$$\begin{aligned} \frac{ \partial u^{(k)}}{\partial t} = \frac{\Vert u^{(k)} \Vert _{TV_{\alpha }(\Omega )}}{\Vert {\textbf{u}} \Vert _{TV_{\alpha }(\Omega )}}\text {div}\left( \frac{\alpha ^{(k)}\nabla u^{(k)}}{|\nabla u^{(k)}|}\right) \quad \text {for } k=1, 2, 3. \end{aligned}$$

For a single channel, we have

$$\begin{aligned} \text {div}\left( \frac{\alpha \nabla u}{|\nabla u|}\right)&= D_{-x}\left[ \dfrac{\alpha _{i,j}D_{+x}u}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 +(D_{0y}u_{i,j})^2 }} \right] \\&\quad + D_{-y}\left[ \dfrac{\alpha _{i,j}D_{+y}u}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j})^2 +(D_{+y}u_{i,j})^2 }} \right] \\&= D_{-x}\left[ \dfrac{\alpha _{i,j}(u_{i+1,j}-u_{i,j})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 +(D_{0y}u_{i,j})^2}} \right] \\&\quad + D_{-y}\left[ \dfrac{\alpha _{i,j}(u_{i,j+1}-u_{i,j})}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j})^2 +(D_{+y}u_{i,j})^2 }} \right] . \end{aligned}$$

Note,

$$\begin{aligned}&D_{-x}\left[ \dfrac{\alpha _{i,j} D_{+x}u}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 +(D_{0y}u_{i,j})^2 }} \right] \\&\quad = D_{-x}\left[ \dfrac{\alpha _{i,j} (u_{i+1,j}-u_{i,j})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \right] \\&\quad = D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i+1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j,k})^2 }} \right] \\&\qquad - D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i,j}}{\sqrt{\varepsilon ^2 +(D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \right] \end{aligned}$$

Apply backward difference on each term separately we obtain

$$\begin{aligned}&D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i+1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \right] \\&\quad =\dfrac{\alpha _{i,j} u_{i+1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \\&\qquad - \dfrac{\alpha _{i-1,j}u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i-1,j})^2 + (D_{0y}u_{i-1,j})^2}} ,\\ \end{aligned}$$

and

$$\begin{aligned}&D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \right] \\&\quad = \dfrac{\alpha _{i,j} u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \\&\qquad - \dfrac{\alpha _{i-1,j} u_{i-1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i-1,j})^2 + (D_{0y}u_{i-1,j})^2}}. \end{aligned}$$

Note that $D_{+x}u_{i-1,j}=D_{-x}u_{i,j}$ and thus,

$$\begin{aligned}&D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i+1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \right] \\&\quad =\dfrac{\alpha _{i,j} u_{i+1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \\&\qquad - \dfrac{\alpha _{i-1,j} u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{-x}u_{i,j})^2 + (D_{0y}u_{i-1,j})^2 }},\\&D_{-x}\left[ \dfrac{\alpha _{i,j} u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \right] \\&\quad = \dfrac{\alpha _{i,j} u_{i,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \\&\qquad - \dfrac{\alpha _{i-1,j} u_{i-1,j}}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i-1,j})^2 + (D_{0y}u_{i-1,j})^2 }}, \end{aligned}$$

and,

$$\begin{aligned}&D_{-x}\left[ \dfrac{\alpha _{i,j}(u_{i+1,j} - u_{i,j})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2}} \right] \\&\quad = \dfrac{\alpha _{i,j}(u_{i+1,j} - u_{i,j})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j})^2 + (D_{0y}u_{i,j})^2 }} \\&\qquad - \dfrac{\alpha _{i-1,j}(u_{i,j} - u_{i-1,j})}{\sqrt{\varepsilon ^2 + (D_{-x}u_{i,j})^2 + (D_{0y}u_{i-1,j})^2}} . \end{aligned}$$

Therefore,

$$\begin{aligned}&\text {div}\left( \frac{\alpha _{i,j}\nabla u^k}{|\nabla u|}\right) \\&\quad = D_{-x}\left[ \dfrac{\alpha _{i,j} (u_{i+1,j}^{k}-u_{i,j}^{k})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j}^{k})^2 +(D_{0y}u_{i,j}^{k})^2 }} \right] \\&\qquad + D_{-y}\left[ \dfrac{\alpha _{i,j}(u_{i,j+1}^{k}-u_{i,j}^{k})}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j}^{k})^2 +(D_{+y}u_{i,j}^{k})^2 }} \right] \\&\quad =\left[ \dfrac{\alpha _{i,j}(u_{i+1,j}^{k} - u_{i,j}^{k})}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j}^{k})^2 + (D_{0y}u_{i,j}^{k})^2 }} \right. \\&\qquad \left. - \dfrac{\alpha _{i-1,j}(u_{i,j}^{k} - u_{i-1,j}^{k})}{\sqrt{\varepsilon ^2 + (D_{-x}u_{i,j}^{k})^2 + (D_{0y}u_{i-1,j}^{k})^2 }} \right] \\&\qquad +\left[ \dfrac{\alpha _{i,j}(u_{i,j+1}^{k} - u_{i,j}^{k})}{\sqrt{\varepsilon ^2 +(D_{0x}u_{i,j}^{k})^2 + (D_{+y}u_{i,j}^{k})^2 }} \right. \\&\qquad \left. - \dfrac{\alpha _{i,j-1}(u_{i,j}^{k} - u_{i,j-1}^{k})}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j-1}^{k})^2 + (D_{-y}u_{i,j}^{k})^2}} \right] \\&\quad = \left[ \alpha _{i,j}{C_E}(u_{i+1,j}^{k} - u_{i,j}^{k}) - \alpha _{i-1,j}{C_W}(u_{i,j}^{k} - u_{i-1,j}^{k}) \right] \\&\qquad + \left[ \alpha _{i,j}{C_S}(u_{i,j+1}^{k} - u_{i,j}^{k}) - \alpha _{i,j-1}{C_N}(u_{i,j}^{k} - u_{i,j-1}^{k}) \right] \\&\quad = \alpha _{i-1,j}{C_W} u_{i-1,j}^{k} + \alpha _{i,j}({C_E}u_{i+1,j}^{k} + {C_S}u_{i,j+1}^{k})\\&\qquad + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k} - (\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S} \\&\qquad + \alpha _{i,j-1}{C_N})u_{i,j}^{k} \end{aligned}$$

where

$$\begin{aligned} C_E&= \dfrac{1}{\sqrt{\varepsilon ^2 + (D_{+x}u_{i,j}^{k})^2 + (D_{0y}u_{i,j}^{k})^2 }},\\ C_W&= \dfrac{1}{\sqrt{\varepsilon ^2 + (D_{-x}u_{i,j}^{k})^2 + (D_{0y}u_{i-1,j}^{k})^2 }},\\ C_S&= \dfrac{1}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j}^{k})^2 + (D_{+y}u_{i,j}^{k})^2 }}, \\ C_N&= \dfrac{1}{\sqrt{\varepsilon ^2 + (D_{0x}u_{i,j-1}^{k})^2 + (D_{-y}u_{i,j}^{k})^2}}, \end{aligned}$$

for $\quad k=1,2,3.$ Thus,

$$\begin{aligned} \frac{ \partial u^{(k)}}{\partial t}&= \frac{\Vert u^{(k)} \Vert _{TV_{\alpha }(\Omega )}}{\Vert {\textbf{u}} \Vert _{TV_{\alpha }(\Omega )}}\text {div}\left( \frac{\alpha ^{(k)}\nabla u^{(k)}}{|\nabla u^{(k)}|}\right) \\&=R(u^{k})\text {div}\left( \frac{\alpha ^{(k)}\nabla u^{(k)}}{|\nabla u^{(k)}|}\right) \end{aligned}$$

is discretized as

$$\begin{aligned}&\frac{u_{i,j}^{k,n+1}-u_{i,j}^{k,n}}{\tau } \\&\quad = R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} + {C_S}u_{i,j+1}^{k,n}) \\&\qquad +\alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n} - (\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} \\&\qquad + \alpha _{i,j}{C_S} + \alpha _{i,j-1}{C_N})u_{i,j}^{k,n+1}\Big ]\\&u_{i,j}^{k,n+1} \\&\quad = u_{i,j}^{k,n} + \tau R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} + {C_S}u_{i,j+1}^{k,n}) \\&\qquad + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n} - (\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S}\\&\qquad + \alpha _{i,j-1}{C_N})u_{i,j}^{k,n+1}\Big ] \end{aligned}$$

Note, $\Vert {\varvec{u}} \Vert _{TV (\Omega )}:=\left[ \sum _{k=1}^3 \left( \int _{\Omega } |\nabla u^{(k)}|\right) ^2 \right] ^{\frac{1}{2}} = \left[ \sum _{k=1}^3 \left( \sum _{i,j} |\nabla u_{i,j}^{k}|\right) ^2 \right] ^{\frac{1}{2}}$ and $\Vert u^k \Vert _{TV (\Omega )}:= \int _{\Omega } |\nabla u^{k}| = \sum _{i,j} |\nabla u_{i,j}^{k}|$ Thus,

$$\begin{aligned} R(u^{k,n}) = \frac{\Vert u^{(k)} \Vert _{TV_{\alpha }(\Omega )}}{\Vert {\textbf{u}} \Vert _{TV_{\alpha }(\Omega )}} = \frac{\sum _{i,j} |\nabla u_{i,j}^{k}|}{\left[ \sum _{k=1}^3 \left( \sum _{i,j} |\nabla u_{i,j}^{k}|\right) ^2 \right] ^{\frac{1}{2}}} \end{aligned}$$

Hence,

$$\begin{aligned} u_{i,j}^{k,n+1}&=u_{i,j}^{k,n} + \tau R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} \\&\quad + {C_S}u_{i,j+1}^{k,n}) + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n}\\&\quad - (\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S} + \alpha _{i,j-1}{C_N})u_{i,j}^{k,n+1}\Big ]\\ \text {i.e. }&u_{i,j}^{k,n+1} + (\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S} + \alpha _{i,j-1}{C_N})u_{i,j}^{k,n+1}\\&\quad =u_{i,j}^{k,n} + \tau R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} + {C_S}u_{i,j+1}^{k,n}) + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n}\Big ]\\ \text {i.e. }&(1+\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S} + \alpha _{i,j-1}{C_N})u_{i,j}^{k,n+1}\\&\quad =u_{i,j}^{k,n} +&\tau R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} + {C_S}u_{i,j+1}^{k,n}) + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n}\Big ] \end{aligned}$$

This leads to the final discretization as follows

$$\begin{aligned} u_{i,j}^{k,n+1}=\frac{u_{i,j}^{k,n} + \tau R(u^{k,n})\Big [ \alpha _{i-1,j}{C_W} u_{i-1,j}^{k,n} + \alpha _{i,j}({C_E}u_{i+1,j}^{k,n} + {C_S}u_{i,j+1}^{k,n}) + \alpha _{i,j-1}{C_N} u_{i,j-1}^{k,n}\Big ]}{(1+\alpha _{i,j}{C_E} +\alpha _{i-1,j}{C_W} + \alpha _{i,j}{C_S} + \alpha _{i,j-1}{C_N})} \end{aligned}$$

Appendix C: Experiments with the Real Data

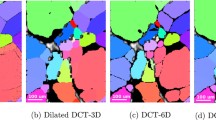
See Figure 7.

Fig. 7

Results of denoising real EBSD map using various filters

Appendix D: Grain Boundaries After Restoration

In this section, we demonstrate the effect of the algorithms on the boundaries of the restored EBSD maps. We found the location of the boundaries using the Farid edge detector [20]. We see in Fig. 8 the details of the boundaries of ESBD maps shown in Fig. 2. Figure 9 shows the details of the boundaries of maps in Fig. 3. The yellow color in Figs. 8 and 9 indicates the locations where the boundaries from the restored maps match the true boundaries exactly. The red color indicated the true boundaries from the clean EBSD map. Thus, the red-colored pixels in images (b) - (h) in Figs. 8 and 9 show locations of the true boundaries that are missed by the algorithms. The green boundaries are the ones obtained from the restored algorithms. Thus, the green-colored boundaries in images (b) to (h) in Figs. 8 and 9 are the incorrect locations of the boundaries found by the corresponding algorithms. We can infer from these images that the boundaries found by the proposed algorithm are comparable in their accuracy with other algorithms discussed in this paper.

Fig. 8

Details of the grain boundaries of EBSD map from Fig. 2. The yellow color represents accurate boundary detection. Red represents true grain boundaries that are missed by the algorithms. Green represents boundaries obtained by the corresponding algorithms which do not match the ground truth

Fig. 9

Details of the grain boundaries of EBSD map from Fig. 3. The yellow color represents accurate boundary detection. Red represents true grain boundaries that are missed by the algorithms. Green represents boundaries obtained by the corresponding algorithms which do not match the ground truth