Calcium-Treated Steel Cleanliness Prediction Using High-Dimensional Steelmaking Process Data

Abstract

Control of calcium treatment in steel is challenging due to the reactivity of Ca and difficulty of measuring total oxygen of steel in-process to make actionable decisions. In this work, a method combining statistics and process engineering are developed using partial least squares regression (PLS) to predict non-metallic inclusion content (oxides and CaS) and composition at the end of ladle treatment and in the tundish using extensive process data and SEM/EDS-based non-metallic inclusion analysis. Total oxygen at the end of the ladle treatment can be predicted to an accuracy of 7 ppm, and the Mg/(Mg+Al) ratio in inclusions to an accuracy of 3at% providing enough data to recommend Ca addition based on a thermodynamic calculation for the Ca liquid window. Alternatively, the model can predict total inclusion fraction to 20 ppm accuracy, and accurately predict average CaS content and Ca/Al ratio of inclusions in the tundish. Model interpretability is hindered by high dimensionality and multicollinearity of the data. Non-metallic inclusion compositions correspond to the expected composition at the onset of CaS formation based on steel composition.

Introduction

Steel Cleanliness and Process Fundamentals

The work presented here concerns control of the oxide cleanliness in steel. “Oxide cleanliness” refers to the concentration and composition of oxide inclusions in the steel. The inclusions mainly originate from dissolved oxygen that is present in the steel after primary steelmaking (which takes place in an electric arc furnace for the plant studied here). The oxygen is removed from solution (in the steel) by introducing aluminum, which reacts with the dissolved oxygen to form aluminum oxide (alumina) inclusions. The majority of the alumina is removed from the steel (by argon stirring and buoyancy), but some alumina inclusions do remain in the steel. Calcium treatment is subsequently applied to modify the composition of these remaining oxide inclusions. The aim of the work was to evaluate the predictability of oxide inclusion composition and concentration, based on available process data.

The purpose of Ca-treatment in steelmaking is to convert hard and solid (at steelmaking temperatures) dispersed oxide inclusions, such as alumina (Al₂O₃) and spinel (MgAl₂O₄), into liquid calcium aluminate inclusions [1]. Al₂O₃ inclusions form when aluminum is added to deoxidize the steel after steelmaking; subsequently the Al₂O₃ partially or fully transforms to MgAl₂O₄ by reaction of magnesium that dissolves into the steel (from slag and/or refractory) during ladle treatment [2]. It is a decades-old challenge to control Ca treatment of steel—the high reactivity of Ca toward O and S and, consequently, it is very low solubility in steel makes it hard to predict exactly how Ca will react with the steel and its surroundings.

Upon introduction into the steel, Ca (in the form of elemental Ca, or CaSi₂) will react with surrounding [O] and [S] and form CaS/CaO nuclei. (The square parenthesis indicates elements dissolved in steel.) The composition of these initial nuclei will depend on the initial [S] and [Al] of steel, and its stability will follow the reaction:

$$\left(\mathrm{CaO}\right)+\left[\mathrm{S}\right]+\left[\mathrm{Al}\right]=\left(\mathrm{CaS}\right)+({\mathrm{Al}}_{2}{\mathrm{O}}_{3})$$

(1)

where the species in parenthesis () denote immiscible phases in steel, while the squared brackets [] denote species dissolved in the liquid steel.

Eventually, inclusions will react toward equilibrium with their surrounding steel. If there is more Al or S dissolved in steel, the equilibrium of this reaction will also be shifted to the right. If CaS is stable, all Ca added to steel will further react with S to form CaS. If CaS is not stable, Ca will react with O, forming Ca-aluminates.

One of the aims of calcium treatment is to ensure even flow of steel toward and into the continuous caster, which is used to solidify the steel. Work done by Story et al. [3] shows the impact of CaS versus oxide stability on steel quality and processability. There is an optimal oxide inclusion window to prevent erosion and clogging simultaneously. (“Clogging” refers to blockage of the ceramic tubes that convey the steel between different vessels, and “erosion” to wear of these ceramic tubes.) Less than 60 ppm of CaS (volume fraction, measured as an area fraction on a polished sample) is desirable for mold level control (in the caster) and mitigation of macro-inclusions and surface defects, and reducing the amount of Ca added to steel is an effective way of reducing the amount of CaS formed in the steel.

The difficulties of predicting the outcome of Ca treatment due to the low solubility of Ca and difficulty to control total oxygen in steel have been discussed in [4]. With the advent of data analysis techniques and computational power that is sufficient to incorporate most of plant data collected by sensors, this work aims to predict the outcome of Ca treatment taking advantage of a vast amount of process data.

Methodology

Experimental Design for Plant Sampling

The studied plant consists of one 95t Electric Arc Furnace (EAF), a Ladle Metallurgical Furnace (LMF) equipped with a turret that is capable of accommodating two ladles, one in staging position and another in processing position, and a 3-strand round billet caster. For building the model, lollipop samples (samples taken from low-mid carbon, micro-alloyed, Al-deoxidized and Ca-treated liquid steel) were collected from 50 heats, at several stages of processing: 1) The end of EAF process (sample P1), 2) samples LX from the ladle after tap (L1, L2, L3, etc.), and 3) sample T2 from the tundish. The samples were collected from the same grade of steel. Of the heats sampled, 29 were produced on the day immediately prior to a steelmaking shop maintenance stoppage (down day) and 21 heats on the day following the stoppage. This sampling methodology was adopted to ensure there is some process variability in the data, otherwise the model would have a very strong bias to “steady state” production performance; process outliers would help with generalizing the model to a wider range of process conditions.

Non-Metallic Inclusion Analysis–Sample Preparation

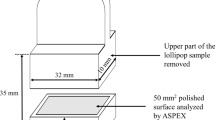
Lollipop samples from the end of ladle treatment (L3) and tundish (T2) were cut twice transversely using a high-speed cutoff saw, to reveal the cross section. A transversal and lengthwise cut are performed so a piece containing the surface to be analyzed fitted a metallographic mount. The sample was mounted face down in conductive thermosetting resin. The sample was then ground and mirror-polished to 1 micron (with diamond paste) using an automatic polisher. The typical sampling position is shown schematically in Fig. 1.

Fig. 1

Schematic of analysis position in lollipop sample, with a typical backscattered electron image of a detected inclusion

Analysis

The mounted samples were analyzed using an ASPEX Explorer scanning electron microscope (SEM). Automated inclusion analysis was used, in which potential inclusions (“features”) are detected from back-scattered electron imaging, and analyzed by energy dispersive X-ray microanalysis (EDX). For each sample, an area of 15–20 mm² was analyzed to ensure at least 1000 particles were found to collect enough statistics for composition and size distributions. The analyses were performed using accelerating voltage of 20 kV, spot size of 25% and working distance of 15 mm. For each sample analyzed, the contrast was set to 100%, and the spot size was finely tuned to calibrate the contrast between the iron matrix of the steel sample and a piece of Al tape attached to the sample surface. For the contrast calibration, the Fe grayscale value was set to 170, and the Al grayscale value to 40. The detection and measurement threshold was set to pick features with grayscale values lower than 135. The magnification was set to 400 × with a 512 × 512 window, giving a search pixel size of 0.78 micron, with expected resolution of 0.5 micron [5].

Data Processing

Calculating and Aggregating Inclusion Composition Data

For each lollipop sample, a raw data table was generated, containing the X and Y position, and the morphological and chemical measurements of each of the features in the analyzed area. Due to the presence of porosity, dust particles and other debris, false positives had to be distinguished from the actual inclusions. Also, TiN and MnS (that precipitate during solidification) were excluded so only de-oxidation and Ca-treatment inclusions were considered in the analysis. For each sample, the inclusions were selected according to the following criteria (applied simultaneously), based on the compositions measured by EDX: wt%Si < 10%; wt%S < 70%; wt%Ca < 70%, wt%Ti < 20%, wt%Mn < 20% and apparent diameter < 15 μm.

Typically, the area-averaged elemental content for all the inclusions in each sample was calculated using the following equation, in which $I$ is the area-averaged elemental composition in weight percentage for the element $i$, present in inclusion $n$ of total inclusion number of $k$, each inclusion having an area of $S$ (in square microns).

$$I=\frac{{\sum }_{n=0}^{k}\left({S}_{n}{i}_{n}\right)}{{\sum }_{n=0}^{k}\left({S}_{n}\right)}$$

(2)

The total mass fraction of inclusions W_f was estimated from the total area fraction of inclusions A_f, given by the following equations, where S_sample is given in square millimeters to yield a fraction in parts per million (by mass); ${\rho }_{incl}$ is the density of inclusions (2.6 g/cm³ for CaS, 3 g/cm³ for Ca-aluminates and 3.6 g/cm³ for spinels), and ${\rho }_{steel}$ is the density of the steel matrix (7.9 g/cm³):

$${A}_{f}=\frac{{\sum }_{n=0}^{k}\left({S}_{n}\right)}{{S}_{sample}}$$

(3)

$${W}_{f}=\frac{{A}_{f}{\rho }_{incl}}{{A}_{f}{\rho }_{incl}+\left({10}^{6}-{A}_{f}\right){\rho }_{steel}}$$

(4)

The mass fraction of a bound element in inclusions [I], relative to the steel mass, is then given by the following:

$$\left[I\right]=\frac{{W}_{f}*I}{100}$$

(5)

The inclusion composition as analyzed by SEM/EDS is subject to matrix effects due to the heavy atoms of Fe attenuating the generated X-rays from the matrix-inclusion-beam interaction, especially when analyzing low energy X-rays from light elements such as Al, Mg, Ca and S that constitute most of the inclusions in steel. While the estimated concentration of bound elements is done by the method shown above, the best estimate for the actual Ca/Al ratio in Ca-treated samples and Mg/Al ratio in ladle samples is found by sampling the mode from the chemical composition distribution, which typically coincides with the composition of larger inclusions (which are less subject to matrix effects in composition).

Extraction of Relative Chemical Composition Data

Mixed inclusions can be subject to analysis artifacts, and the EDS quantification of relative quantities of elements with higher energy vs. lower energy (such as Ca versus Al) can show large spread. In order to mitigate such effects, Ca/Al ratios and Mg/Al ratios are collected from the distribution of inclusions containing mostly pure oxides. The pseudo-algorithm for such procedure is summarized below.

• 1. Read non-metallic inclusion analysis dataframe;

• 2. Filter inclusions with more than 10%S in their composition to remove sulfides from the analysis;

• 3. For each individual inclusion, calculate the molar ratio as Ca/(Ca + Al);

• 4. Perform kernel density estimation of the Ca/(Ca + Al) distribution in the sample;

• 5. Locate the composition correspondent to the distribution maximum value.

The collected composition is then used as the main index for CaO/Al₂O₃ ratio control. The distributions are shown in Fig. 2, and the validation with the thermodynamic model is given later in Fig. 15.

Fig. 2

Ca/(Ca + Al) molar ratio in oxide inclusions for all analyzed samples. a Histogram, b kernel density estimation for the distributions in a

Indexing Argon Stirring to Their Respective Processes

Due to some idiosyncrasies of data, indexing the actual argon profile to its heat from end of EAF process to the start of casting is a challenge. (Briefly, the argon flow rate to the turret is recorded, without it being clear in the data which ladle—or heat—is receiving the argon.) Indexing was performed, based on the following process steps:

• 1. Electric arc furnace steel is sampled for composition, temperature and oxygen at the heat end;

• 2. Steel is tapped into a ladle, and Al, SiMn, carbon, FeCr and calcium aluminate flux are added (upon EAF fastback the heat ID change is triggered);

• 3. The steel ladle waits in the ladle car until the current heat at the staging turret turns into the LMF processing position;

• 4. The steel ladle waits on the turret until the current heat in the LMF departs to the caster, with some Argon stirring performed at the staging position;

• 5. The steel ladle goes to the LMF processing position (LMF heat ID change is triggered);

• 6. The steel ladle goes to caster (caster heat ID change is triggered).

Any argon stirring performed between steps 2 and 5 is unassigned to any heat IDs. Stirring performed outside the turrets (in the ladle car) is also unassigned. Therefore, if one slices the Ar flowrate time-series data only for the LMF heat number timestamps, a large portion of the Ar stirring process would not be considered in the calculations. However, the argon lines are assigned to each turret position (turret #1 and #2); a tag from the time-series data “LMF_Tx_In_Position” (where x can be 1 or 2) is used to identify and assign the Ar line used for that specific heat being processed.

The process is described as follows:

• The timestamp for the end of EAF process and the timestamp for the start of casting of heat X are collected (and total ladle contact time is recorded);

• The average ‘LMF_Tx_In_Position’ is calculated for that LMF heat. Based on the binary result (0 means not in processing position, 1 means in processing position), then the proper Ar line data (flowrate and backpressure) is assigned to a heat number.

The ladle car stirring profile is calculated by slicing the ladle car argon flowrate between 8 min before and 4 min after the end of EAF processing as recorded by the system. The full stirring profiles after assignment are shown in Fig. 3. Zero time is taken four minutes before the start of tapping from the EAF to capture the initial stirring profile.

Fig. 3

Visualization of Ar stirring flowrate (cubic feet per minute) for 50 heats over time, showing some process variability for the stirring process

Data Pre-Processing Procedure

The procedure to convert data into a format that can be fed to a regression model is described below:

• 1. Point data tables (e.g., additions, temperature measurements and chemical analyses) are joined by heat number (ID);

• 2. Data tables with multiple measurements (composition, additions, temperature, kWh in LMF) are converted into time-series, that is, a format where there is a timestamp column and a tag value column (each tag is an element, temperature or energy consumption measurement).

• 3. Timestamps for each heat are sliced from the end of EAF processing (tap) to the beginning of casting;

• 4. A table (dataframe) is created for each heat, where the row index is the timestamp of the recorded data and each column is a process variable (point data are the same value repeated across all rows).

• 5. Time relative to tap and de-oxidation are calculated.

• 6. Categorical variables such as ladle ID, lance status and crew ID are encoded into binary (a.k.a. dummy) variables, in which each category becomes a separate column.

• 7. Variables such as ladle additions, argon stirring, and energy consumption are treated as cumulative variables to facilitate time-series treatment and resampling.

• 8. A dictionary of process variables (as dataframes) is generated, where each dataframe is one process variable, but each column is a timestep and each row is a single heat. This is performed to create variable blocks that can be easily implemented in a multi-block partial least squares regression approach (Fig. 4).

• 9. Data tables are then aligned across heats (that means the heats are compared at the same time after tap, to capture process variability over time).

Fig. 4

Block variable scheme used for PLS regressions, where p is the number of observations and t is the number of timesteps

Modeling

Domain knowledge is a fundamental part of the construction of a potentially interpretable model, and also to make sure the predictions are in accordance with the laws of physics and thermodynamics. Also, the calculation of the minimum required Ca addition uses reaction thermodynamics, and uses the predicted concentration of oxygen bound in inclusions is one of the inputs. Therefore, relevant metallurgical models in accordance with the current scientific understanding of inclusion engineering are implemented and added as variables to the statistical model.

Metallurgical Features Added to the Model

Desulfurization Mass Transfer Coefficient

Desulfurization follows first-order reaction kinetics [6, 7], with the decrease in sulfur concentration in steel given by the following kinetic equation, in which [S], [S]₀ and ${\left[S\right]}_{\infty }$ are, respectively, the present, initial and equilibrium content of sulfur in steel; k is the desulfurization rate constant (in 1/s) and t and t₀ are, respectively, the current sampling time and time at the first chemical sample:

$$\mathrm{ln}\left(\frac{\left[\mathrm{S}\right]-{\left[\mathrm{S}\right]}_{\infty }}{{\left[\mathrm{S}\right]}_{0}-{\left[\mathrm{S}\right]}_{\infty }}\right)=-k(t-{t}_{0})$$

(6)

For the typical slag composition, the equilibrium sulfur at the end of ladle treatment is calculated by FactSage 8.0 to be 11 ppm. Applying this equilibrium concentration to all heats, for each heat the measured values of [S] and their timestamps are substituted in the kinetic equation, and the calculated slope is the rate constant (k, units of 1/s) of the heat. If the rate constant is larger, that means the desulfurization progressed faster, therefore the steel-slag reactions were performed more efficiently. A higher observed rate constant usually means a combination of faster steel mass transfer to the interface and steel-slag interface breakup. The rate constant can be compared with empirical estimates derived from the ladle dimensions and the Ar flowrate at that time in the process. Comparison with plant data showed that for Ar stirring rates of up to 10 NL/min.t (or 30 CFM) on heats with good plug conditions, the empirical estimations and actual measurements correlate well, showing that desulfurization is limited by mass transfer. The rate constant is added to the model as a single average variable (for each heat).

Slag Mass Balance and Solids Estimation

One of the governing phenomena for steel cleanliness (and desulfurization) is slag de-oxidation; high FeO and MnO concentrations in slag (reducible oxides) will consume Al, hindering desulfurization and preventing the dissolved oxygen in the steel from reaching desired values. The residual FeO and MnO most originate from the furnace slag carried over during tapping of the electric arc furnace—typical amounts of carry-over slag can range from 2 to 10 kg of slag/t of steel [8]. The slag carry-over forms the basis of final LMF slag, with the slag composition adjusted by the addition of de-oxidation products (Al₂O₃ and SiO₂ formed from Al and SiMn additions), and with the slag basicity and MgO content adjusted by flux additions. A reliable estimate for slag volume is fundamental to calculate the fraction of solids in slag, which usually is not directly detected by chemical composition measurement (i.e., X-ray fluorescence spectroscopy). An excessive concentration of solids in slag can hinder desulfurization and lead to an operational response in form of late alloy additions and overstirring of steel, which can have detrimental consequences for steel cleanliness due to re-oxidation and slag entrainment.

A simplified aluminum balance was found to be the most reliable index to estimate slag carry-over volume (other balances that were assessed were those of manganese and phosphorus). The balance is shown below, in terms of mass percentages, in which [i]_X is the amount relative to steel mass of chemical species i consumed in process X, (i)_X is the amount relative to slag mass of chemical species i consumed in process X and M_i is the molar mass of the chemical species i.

$${\left[\mathrm{Al}\right]}_{\mathrm{added}}={\left[\mathrm{Al}\right]}_{\mathrm{steel\,deox}.}+{\left[\mathrm{Al}\right]}_{\mathrm{slag\,deox}.}+{\left[\mathrm{Al}\right]}_{\mathrm{alloy}}+{\left[\mathrm{Al}\right]}_{\mathrm{de}-\mathrm{S\,at\,tap}}$$

(7)

$${\left[\mathrm{Al}\right]}_\text{steel deox}={0.0001\left[\mathrm{O}\right]}_{Celox, \mathrm{ppm}}*\frac{2{M}_{\mathrm{Al}}}{3{M}_{\mathrm{O}}}$$

(8)

$${\left[\mathrm{Al}\right]}_\text{added}=100\frac{{W}_\text{total {Al} added at tap}}{{W}_\text{steel after tap}}$$

(9)

$${\left[\mathrm{Al}\right]}_\text{de-S}=\left({\left[\mathrm{S}\right]}_\text{after tap}-{\left[\mathrm{S}\right]}_{EAF}\right)*\frac{2{M}_{\mathrm{Al}}}{3{M}_{\mathrm{S}}}$$

(10)

Since the [Al] that alloys the steel is directly measured by optical emission spectroscopy (OES), the remaining aluminum loss is taken to be Al consumed by slag de-oxidation. The amount of oxygen to be reduced from the slag can be estimated from the following:

$$(\%\mathrm{O})=\left(\left(\%\mathrm{FeO}\right)*\left(\frac{{M}_{\mathrm{O}}}{{M}_{\mathrm{FeO}}}\right)+\left(\%\mathrm{MnO}\right)*\left(\frac{{M}_{\mathrm{O}}}{{M}_{\mathrm{MnO}}}\right)\right)$$

(11)

The amount of oxygen consumed by the Al during slag de-oxidation is given by:

$${\left[\mathrm{O}\right]}_\text{slag}={\left[\mathrm{Al}\right]}_\text{slag deox}*\frac{3{M}_{\mathrm{O}}}{2{M}_{\mathrm{Al}}}$$

(12)

The amount of oxygen that reacts with Al in the steel (expressed as a percentage of steel) is also directly related to the amount of slag carry-over:

$${\left[\mathrm{O}\right]}_\text{slag}=\frac{{W}_\text{slag carry-over}}{{W}_{steel}}(\%\mathrm{O})$$

(13)

The slag carry-over amount must be corrected for its composition after de-oxidation. The assumption is that FeO and MnO are fully reduced by Al to form Al₂O₃. The distribution of the results for the analyzed heats is shown in Fig. 5.

Fig. 5

Histogram showing estimated slag carry-over for the analyzed heats, with average value of 7.6 kg per metric ton of liquid steel (‘tls’). Blue solid line is the kernel density estimation (KDE) for the distribution

The fraction of solids (solids index, written as SI) added to the slag is then calculated using the following relationship. In this expression, W_flux is the mass of calcium aluminate flux added to the ladle. (Calcium aluminate is liquid at steelmaking temperatures.)

$$SI=\frac{{W}_\text{lime}+{W}_{\text{MgO}}}{{W}_\text{slag carry-over, deoxidized}+{W}_\text{flux}}$$

(14)

Statistical Modeling

Overall Model Structure

Obtaining non-metallic inclusion data limits the number of observations since it is not a routine production quality assessment in the plant; also, if one wants to carry quantitative analysis using SEM/EDS, execution must be consistent. Therefore, the problem becomes a high dimensional, low sample size one (or HDLSS). That is, predictors outnumber observations (p > n).

The selected strategy to overcome the HDLSS problem is to select a regression method that reduces dimensionality. Ordinary least squares methods (OLS) such as LASSO, ridge regression and ElasticNet [9] are methods in which regularization is tuned to select a set of predictors that has optimal cross-validation values. Alternatively, partial least squares regression (PLS) is a method that decomposes the high-dimensional space of variables to a lower dimensional space so that the predictor matrix X and response matrix Y have their covariance maximized. In this case, the hyperparameter to be tuned is the number of components in the projection (the latent variables, abbreviated as LVs) [10, 11].

Steel production data are strongly collinear—to avoid disruptions, most actions taken in process (such as alloy and flux additions) are performed in tight timeframes, so data step changes overlap in their timelines. Due to the small sample size and high dimensionality of data, traditional OLS regressions (LASSO, ridge, and ElasticNet) failed to converge and did not generate stable solutions for the inclusion prediction problem with the current dataset. Partial least squares, due to its decomposition procedure, picks up slight differences in data and exaggerates them (by covariance maximization of the dataset). Therefore, the model relies on these features and their linear interactions.

This work focuses on the utilization and optimization of PLS regression to predict inclusion composition in steel.

Backward Variable Selection with Selection of Optimal Number of PLS Components

Feature selection must be performed in such high-dimensional problems to reduce overfitting and enable interpretability of the model. In this work, backward variable selection [12] is used to remove the variables that explain the least of the variance in the response (that is, whose regression coefficients are closer to zero) for a set of number of latent variables (for example, from 1 to 10 LVs). At each iteration of number of LVs and variable sets, cross-validation is performed. The final selected model is the one that performs with the smallest cross-validation error (the model with minimum overfitting). Cross-validation for model selection is performed using a fivefold scheme.

Response Variables

A separate model is generated for every inclusion feature to be predicted. In this work, results for the following are presented:

• Bound oxygen concentration before Ca treatment;

• Molar Mg/(Mg + Al) ratio in oxide inclusions before Ca treatment;

• Average mass fraction of CaS in inclusions after Ca treatment;

• Molar Ca/(Ca + Al) ratio in oxide inclusions after Ca treatment;

• Bound oxygen concentration after Ca treatment;

• CaS and oxide area fraction after Ca treatment.

The overall modeling scheme is shown in Fig. 6.

Fig. 6

Modeling scheme selected for this work

Results

Cleanliness Baselines

In Figs. 7 and 8, the steelmaking process cleanliness baselines are shown, where “cleanliness” refers to the concentration of solid inclusions (represented by bound oxygen), and the composition of those inclusions (both the oxidic part of the inclusions, and CaS). The interquartile range of apparent bound oxygen by SEM/EDS before Ca-treatment is between 9 and 16 ppm [O], being narrowed down to 9 and 14 ppm [O] in tundish samples. According to these results, the amount of bound oxygen does not vary significantly from ladle to tundish—however, they do not correlate. That means there are other factors at play between the extraction of the ladle sample and the tundish sample. The average molar fraction of Mg in alumina/spinel inclusions ranges from 0.21 to 0.25, indicating that there is incomplete transformation from alumina to spinel. In practice, that means there must be small concentrations of dissolved Mg in steel before calcium treatment.

Fig. 7

Non-metallic inclusion composition baselines before Ca treatment

Fig. 8

Non-metallic inclusion composition baselines after Ca-treatment (tundish samples)

After Ca treatment, the average amount of CaS relative to other inclusion oxides (mostly CaO, MgO and Al₂O₃) has an interquartile range between 35 and 45%, but these values can range up to 60%. The large range also provides enough variability to ensure good prediction by the developed model. The average Ca/(Ca + Al) ratio in the oxide portion of inclusions is mostly between 48 and 56%–since all samples are CaS-saturated, these composition differences must relate to the chemical composition of steel itself, more specifically [Al] and [S] in steel. More discussion on this is provided below.

From Figs. 9 and 10, it appears that the oxide cleanliness (expressed as ppm of bound oxygen) in the tundish correlates with oxide cleanliness in the ladle, if the bound oxygen concentration in the steel is lower than 7.5 ppm O in the ladle sample; this correlation is indicated by formation of more CaS upon Ca treatment. (The principle is that, if less bound oxygen is present in the ladle before calcium treatment, more CaS would form since less calcium can react with oxide inclusions.) However, for average ladle bound oxygen values around 10 and 20 ppm O, there is no clear correlation between ladle and tundish cleanliness.

Fig. 9

Bound oxygen in ladle sample compared to bound oxygen in tundish sample

Fig. 10

Average %CaS in tundish inclusions compared to measured bound oxygen in ladle sample

Model Performance Using Backward Variable Selection

In order to predict the average inclusion composition after Ca treatment, two approaches were used. The first one is to predict the total O and Mg/(Mg + Al) molar ratio that allows a Ca addition recommendation for the operator together with the previously measured [Al] and [S].

The second approach is to directly predict the inclusions in the tundish based on process data. Since the amount of added Ca was fixed for the whole dataset, the effect of calcium wire amount on the concentration of inclusions and total oxygen cannot be assessed with the collected data.

Predicting Inclusions Before Calcium Treatment

Before Ca treatment, using process data, the predictive performance of the model using fivefold cross-validation is a root-mean-squared error (RMSE) of 7 ppm when predicting the concentration of bound oxygen, and the amount of spinel transformation, expressed as Mg/(Mg + Al), can be predicted to an RMSE of 0.03. The cross-validation results are presented in Fig. 11.

Fig. 11

Fivefold cross-validation of predictions for bound oxygen concentration and Mg/(Mg + Al) ratio from non-metallic inclusion analysis, with optimal number of latent variables and root-mean-squared errors. The blue solid lines are the 1:1 lines

Predicting Inclusions After Calcium Treatment

The predictive power for predicting total oxygen after Ca treatment in the tundish sample is relatively worse, as seen in Fig. 12. Although the RMSE is 3 ppm smaller than for the ladle sample, that is because the variance in data is also smaller. Most of the detected bound oxygen varies between 5 and 15 ppm, with very consistent cleanliness throughout. However, the total area fraction of CaS and oxide inclusions can be predicted with a RMSE of 20 ppm, the average CaS fraction to a RMSE of 4% and the molar Ca/(Ca + Al) fraction to a RMSE of 8%.

Fig. 12

Fivefold cross-validation of predictions for CaS and oxide area fraction, bound oxygen concentration, average CaS fraction and molar Ca/(Ca + Al) fraction after Ca treatment (in tundish sample), with optimum number of latent variables and their respective root-mean squared errors. The blue solid lines are the 1:1 lines

Including casting variables in the prediction does not seem to increase the predictive power of the model (as seen in Fig. 13), but the increase in latent variable number indicates potential overfitting of the model which could hinder its generalization. This is discussed in the following section.

Fig. 13

Fivefold cross-validation of predictions for bound oxygen concentration, average CaS fraction and molar with optimum number of latent variables and their respective root-mean-squared errors—including caster variables. The blue solid line is the 1:1 line

Discussion

Inclusion Predictability from a Steelmaking Perspective

As mentioned earlier, having > 500 variables to regress against 50 observations is a high dimensional, low sample size problem. Because modeling approaches in this context are prone to overfitting, there are some ways to assess how severely the model is overfitted by looking at how correlated these variables are. In a similar fashion to Principal Component Analysis (PCA), the loading vectors of the predictor matrix can be analyzed for their collinearity. As shown in Fig. 14, some of the collinear variables have no explicit real-world correlation, therefore it is an indication of model overfitting. The same is observed when the selected predictors change when other variables are added to the system. For high sample size models, compromising bias for variance can be a valid approach to consider for interpretability—in this case, the cross-validation root-mean-squared errors are acceptable, so such a compromise is not recommended.

Fig. 14

Plot showing first two components for X loading vectors, where each vector represents a variable. More collinear variables explain variance in Y more similarly. a Model for total oxygen in ladle sample; b model for total oxygen in tundish sample (without casting variables); c model for total oxygen in tundish sample (including casting variables)

In Fig. 14, the first two components for the predictor variables for predicting (a) total oxygen in ladle; (b) total oxygen in tundish (without casting variables) and (c) total oxygen in tundish (considering casting variables) are shown. In Fig. 14a, there is a chance the model is more generalized than the models shown in Figs. 14b and c, since in Fig. 14a most variables are non-collinear. However, it is unlikely that variation in Ni or B at earlier stages of refining (represented by _0) have a physical meaning in steel cleanliness, since the usual concentration of these elements do not directly or indirectly change the thermodynamics or kinetics of oxides/sulfides in the presence of low-carbon, Al-killed, Ca-treated steel.

In the case presented in Fig. 14b, temperature, variation in power-on energy, variation in Mn content and Al content at the end of refining are plausible variables to account for the variance in steel cleanliness, since they can relate to re-oxidation and late alloying. Although the cross-validation root-mean-squared error is low for the present data, interpreting their regression coefficients might be a stretch due to the low sample size. To do so, more data points must be collected. Since collection of these data points is expensive and time-consuming, one can induce variance in the data by collecting experimentally designed heats or having a quota for heats where cleanliness problems were detected, with a sufficient number of such heats that a robust model approach would not eliminate those as outliers.

The non-metallic inclusion compositions do predictably respond to process data. In Fig. 15, it is seen that the inclusion modification trajectories indeed follow the expected behavior. In Fig. 16, the oxide portion of inclusions have compatible and predictable compositions using thermodynamics alone, by considering the thermodynamics of CaO reacting with Al and S to form CaS and Al₂O₃, also taking in account the actual temperature and extent of spinel transformation (to account for the activity of Al₂O₃). There is a slight offset from the 1:1 line—this can be due to microscope artifacts such as Ca over-analysis due to the matrix effect (filtering of the Al K-alpha signal).

Fig. 15

Observed non-metallic inclusion average compositions after LMF and tundish, with their respective trajectories shown as gray lines, compared to simulated trajectories using FactSage. Expected average trajectory marked by the red line

Fig. 16

Comparison of calculated Ca/(Ca+O) molar ratio in oxide portion of inclusions with the observed values. Each data point is from a single heat, the red line is the 1:1 line and the blue line is a fitted linear regression (blue shade is the 95% confidence interval for the regression)

Conclusions

Based on the modeling results, some inferences can be made:

• Partial least squares modeling provides satisfactory results in predicting the composition and concentration of non-metallic inclusions. It can predict O at the end of ladle treatment to an RMSE of 7 ppm, and the total area fraction in tundish sample to an RMSE of 20 ppm. It also predicts the relative amount of CaS in tundish sample in inclusions to an RMSE of 4wt% CaS. The Ca/(Ca + Al) ratio is predictable to an RMSE of 0.08, in a range of 0 to 1. These results can be very helpful to indicate the correct trends in non-metallic inclusion formation after Ca treatment as measured in tundish samples.

• The model, however, is not interpretable as it is. This is due to the low sample size, high dimensionality of data and high collinearity of the variables. However, cross-validation results show good predictive power of the model for data in the ranges analyzed, as indicated from the RMSE.

• Non-metallic inclusions before Ca treatment are mostly alumina/spinels, not fully transformed to MgAl₂O₄, and the extent of transformation is correlated to desulfurization extent. Oxygen removal does not appear to be correlated to the desulfurization extent but the total oxygen in the ladle is in the expected range of 10–20 ppm.

• The amount of CaS in inclusions in the tundish is related to total oxygen at the end of ladle treatment.

• The Ca/Al (or Ca/O) ratio in inclusions follows the expected behavior with steel composition, agreeing with the assumption of CaS saturation in steel. Oxide inclusions are mostly liquid and should not present casting problems. To overcome the high dimensionality of the data and the complexity of the calcium treatment process, the dataset must be expanded using routinely collected samples from the steelmaking process, so more process and outcome variabilities are captured to have a explainable and less complex model.

• This model was built upon the variability of the process around a fixed procedure for Ca wire addition, which is the most common scenario in the secondary metallurgy of a steelmaking plant. One possibility is to build a model around the variability of the calcium wire addition procedure, which is usually designed as experiments.