Skip to main content
SpringerLink
Log in

XtalMesh Toolkit: High-Fidelity Mesh Generation of Polycrystals

  • Technical Article
  • Published:
Integrating Materials and Manufacturing Innovation Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

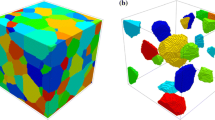
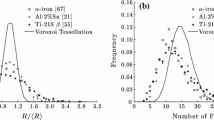
A method for generating high-fidelity, boundary conforming tetrahedral mesh of three-dimensional (3D) polycrystalline microstructures is presented. With growing interest into subgrain scale micromechanics of materials, crystal plasticity finite element (CPFE) models must adapt not only their respective constitutive laws, but also their model geometry to the finer scale, namely the representation of grains and grain boundary junctions. Additionally, with the increasing availability of microstructure datasets obtained via 3D tomography experiments, it is possible to characterize the 3D topology of grains. From these advancements in experiment emerge both an opportunity and challenge for researchers to develop model microstructures, specifically finite element meshes, which best preserve grain topology for the accurate representation of boundary conditions in polycrystalline materials. To accomplish this, an open-source code called XtalMesh was created and is presented here. XtalMesh works by smoothing input voxel microstructure data using a feature-aware Laplacian smoothing algorithm that preserves complex grain topology and leverages state-of-the-art tetrahedralization code fTetWild to generate volume mesh. In this work, the workflow and associated algorithms of XtalMesh are described in detail using a synthetically generated example microstructure. For demonstration, we present a case study involving mesh generation of an experimentally obtained microstructure of nickel-based superalloy Inconel 718 (IN718).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Miao J, Pollock TM, Wayne Jones J (2009) Crystallographic fatigue crack initiation in nickel-based superalloy rené 88dt at elevated temperature. Acta Materialia 57(20):5964–5974

    Article  CAS  Google Scholar 

  2. Stein C, Lee S, Rollett A (2012) An analysis of fatigue crack initiation using 2D orientation mapping and full-field simulation of elastic stress response. Wiley, London

    Google Scholar 

  3. Stinville JC, Martin E, Karadge M, Ismonov S, Soare M, Hanlon T, Sundaram S, Echlin MP, Callahan PG, Lenthe WC, Miller VM, Miao J, Wessman AE, Finlay R, Loghin A, Marte J, Pollock TM (2018) Fatigue deformation in a polycrystalline nickel base superalloy at intermediate and high temperature: competing failure modes. Acta Mater 152:16–33. https://doi.org/10.1016/j.actamat.2018.03.035

    Article  CAS  Google Scholar 

  4. Charpagne M, Hestroffer J, Polonsky A, Echlin M, Texier D, Valle V, Beyerlein I, Pollock T, Stinville J (2021) Slip localization in inconel 718: a three-dimensional and statistical perspective. Acta Materialia 215:117037. https://doi.org/10.1016/j.actamat.2021.117037

    Article  CAS  Google Scholar 

  5. Cubit geometry and meshing toolkit, sandia national laboratories (2019). http://cubit.sandia.gov

  6. Simmetrix inc. simulation modeling suite. http://www.simmetrix.com/

  7. Lee M-J, Jeon Y-J, Son G-E, Sung S, Kim J-Y, Han H, Cho S, Jung S-H, Lee S (2018) Grain boundary conformed volumetric mesh generation from a three-dimensional voxellated polycrystalline microstructure. Met Mater Int. https://doi.org/10.1007/s12540-018-0083-x

    Article  Google Scholar 

  8. Lee S, Rohrer G, Rollett A (2014) Three-dimensional digital approximations of grain boundary networks in polycrystals. Modell Simul Mater Sci Eng 22(2):025017

    Article  Google Scholar 

  9. HyperMesh (2017). https://altairhyperworks.com/product/HyperMesh

  10. Quey R, Dawson P, Barbe F (2011) Large-scale 3d random polycrystals for the finite element method: generation, meshing and remeshing. Comput Methods Appl Mech Eng 200(17):1729–1745. https://doi.org/10.1016/j.cma.2011.01.002

    Article  Google Scholar 

  11. Hart KA, Rimoli JJ (2020) Microstructpy: a statistical microstructure mesh generator in python. SoftwareX. https://doi.org/10.1016/j.softx.2020.100595

    Article  Google Scholar 

  12. Sandström C (2016) Voxel2Tet. https://github.com/CarlSandstrom/Voxel2Tet

  13. Hestroffer JM (2021) XtalMesh https://github.com/jonathanhestroffer/XtalMesh

  14. Merkel D (2014) Docker: lightweight linux containers for consistent development and deployment. Linux J 2014(239):2

    Google Scholar 

  15. Groeber MA, Jackson MA (2014) DREAM3d: a digital representation environment for the analysis of microstructure in 3d. Integr Mater Manuf Innov 3(1):56–72. https://doi.org/10.1186/2193-9772-3-5

    Article  Google Scholar 

  16. Hu Y, Schneider T, Wang B, Zorin D, Panozzo D (2020) Fast tetrahedral meshing in the wild. arXiv:1908.03581

  17. Zhou Q, Jacobson A, Thingi10k: a dataset of 10, 000 3d-printing models, arXiv:abs/1605.04797

  18. Hu Y, Zhou Q, Gao X, Jacobson A, Zorin D, Panozzo D (2018) Tetrahedral meshing in the wild. ACM Trans Graph. https://doi.org/10.1145/3197517.3201353

    Article  Google Scholar 

  19. Rabinovich M, Poranne R, Panozzo D, Sorkine-Hornung O (2017) Scalable locally injective mappings. ACM Trans Graph. https://doi.org/10.1145/2983621

    Article  Google Scholar 

  20. Jacobson A, Kavan L, Sorkine O, Robust inside-outside segmentation using generalized winding numbers. ACM Trans Graph 32 (4)

  21. Stinville J, Hestroffer J, Charpagne M, Polonsky A, Echlin M, Torbet C, Valle V, Shadle D, Nygren K, Miller A, Loghin A, Beyerlein I, Pollock T (2021) Multi-modal dataset of a polycrystalline metallic material: 3d microstructure and deformation fields, in review

  22. Stimpson C, Ernst C, Knupp P, Pébay P, Thompson D (2007) The verdict library reference manual

  23. Ahrens J, Geveci B, Law C (2005) Paraview: an end-user tool for large data visualization. In: The visualization handbook 2005

  24. Stinville J, Charpagne M, Bourdin F, Callahan P, Chen Z, Echlin M, Texier D, Cormier J, Villechaise P, Pollock T, Valle V (2020) Measurement of elastic and rotation fields during irreversible deformation using heaviside-digital image correlation. Mater Character 169:110600. https://doi.org/10.1016/j.matchar.2020.110600

    Article  CAS  Google Scholar 

Download references

Acknowledgements

This work is funded by the U.S. Department of Energy, Office of Basic Energy Sciences Program DE-SC0018901.

Author information

Authors and Affiliations

  1. Materials Department, University of California, Santa Barbara, CA, USA

    Jonathan M. Hestroffer & Irene J. Beyerlein

  2. Department of Mechanical Engineering, University of California, Santa Barbara, Santa Barbara, CA, USA

    Irene J. Beyerlein

Authors
  1. Jonathan M. Hestroffer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Irene J. Beyerlein
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jonathan M. Hestroffer.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Appendix

Appendix

Fig. 12
figure 12

a 3D reconstruction of Tribeam experiment dataset for IN718. b Same Tribeam dataset viewed along the x-direction to visualize the rough surface, this area is filled with voxels until flat. c Tribeam dataset with the new surface “cap” of voxels in dark gray. Dataset obtained from Stinville et al. [21]

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hestroffer, J.M., Beyerlein, I.J. XtalMesh Toolkit: High-Fidelity Mesh Generation of Polycrystals. Integr Mater Manuf Innov 11, 109–120 (2022). https://doi.org/10.1007/s40192-022-00251-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40192-022-00251-w

Keywords

Search

Navigation