Introduction

Laser powder bed fusion (LPBF) or selective laser melting (SLM) is an additive manufacturing (AM) technology where freeform parts are produced by means of a layer-by-layer process. A layer of metal powder is spread over a build plate and a highly localized laser beam selectively melts metal powder particles following a predefined scan strategy. During this process, each material point undergoes rapid melting–solidification cycles generating residual stresses, i.e., stresses which remain in the material at equilibrium. The residual stresses generated during an LPBF process can severely affect the fatigue behavior of the component [1]. Moreover, they might lead to crack generation or large part distortions in the final artifact [2]. Nowadays, the presence of process-dependent residual stresses is one of the main limitations to a widespread adoption of LPBF technology in industrial applications [3].

As thoroughly investigated in the recent literature review of Bartlett and Li [2] on residual stress generation in LPBF processes, direct changes in the energy input generate large variations in the residual stress magnitude since they alter heat transfer conditions and cooling rates. Yeung et al. [4] present the implementation of a set of advanced laser control strategies for LPBF systems. Three laser power and three scan speed control strategies, resulting in nine potential combinations, are implemented on the additive manufacturing metrology testbed (AMMT), an open architecture LPBF machine constructed at the National Institute of Standard and Technology (NIST). The objective of such a work is to assess the influence of the nine laser control strategies on the dynamic melt pool response by means of high-speed thermal camera in situ measurements and confocal microscopy reconstruction of three-dimensional surface topography. Measurements of residual stresses or strains are complex at this scale, require advanced equipment and analyses, and generally cannot provide a fully defined stress tensor field [3]. Therefore, numerical simulations can help to evaluate the effects of laser power and scan speed control strategies on residual stresses.

Modeling and simulating a LPBF process is an extremely challenging task from a computational point of view due to the large variety of spatial and temporal scales involved in the process. Different numerical techniques are adopted depending on the spatial scale we aim at solving. For instance, macro-scale effects are generally simulated employing reduced modeling techniques. Reduced methods in AM simulations can be split into two main groups:

  1. 1.

    models based on the coupling of a local- and a macro-scale simulation (e.g., the modified inherent strain [5, 6], the part-scale model of [7])

  2. 2.

    models based on weakly coupled thermo-mechanical analysis (e.g., the so-called pragmatic approach [8], the volume-by-volume approach [9, 10], and the agglomeration method [11, 12])

All these models are suitable choices if we are interested in predicting global effects.

Conversely, if we are interested in quantifying the influence of the laser scan path or of the laser power and speed on residual stresses, we need to employ numerical and physical models resolving the melt pool length scale. Moreover, if we want to compute a sensitivity study to quantify the effects of input variables on a selected design, several computations of the process have to be performed. To achieve these goals, homogeneous models are generally adopted. They consider a single continuum domain with different material properties for the powder, solid, and liquid regions. Homogeneous models are mainly adopted to study the influence of different scan strategies and other process parameters either on melt pool shapes and cooling rates [13,14,15,16,17,18,19,20,21] or on residual stresses [22,23,24,25,26], and they are generally implemented using weakly coupled thermo-mechanical finite element analysis (FEA).

More complex melt pool-scale models may integrate multiple domain types (e.g., continuum, discrete element, or particle-based), as well as varying physical phenomena (e.g., fluid dynamics, microstructure evolution, etc.) [27,28,29]. However, the relative simplicity and computational efficiency of conduction-based FEA methods enable a more rapid simulation of adjacent laser tracks and multilayer problems. Conduction-based thermal models provide melt pool-scale temperature distribution and response to objective measures such as residual stress and are therefore critical for exploring the effects of complex scan strategies or laser parameter control.

In the present work, we aim at obtaining a residual stress evaluation for the nine different laser scan strategies measured in [4], in order to determine the most effective control strategy reducing residual stresses at the scan island length scale. Numerical prediction of this quantity is highly interesting since it allows to study residual stress of small geometric features in 3D printed structures, e.g., lattice truss. Previous studies presented in [4] were limited to the experimental investigation of the effects of these control strategies on melt pool area variations and surface topography. The results reported in the present work give a new insight into the nine advanced laser scan strategies studying their influence on residual stress as well.

The outline of the paper is as follows. In “Governing Equation” section, the governing equations of the thermo-mechanical problem are introduced. “Implementation of the Laser Control Strategy” section briefly recalls the implementation of the scan control strategy on the AMMT machine as presented in [4]. In “Numerical Implementation” section, the numerical implementation of the physical model is described. In “Results and Discussion” section, firstly we validate the thermal model comparing the simulated melt pool areas with respect to the in situ measurements of the first scan pattern and, secondly, we present and discuss the residual stress results obtained for the nine laser scan strategies. Finally, in “Conclusions” section, we draw our main conclusion, i.e., the fact that constant power density strategy reduces residual stresses more than the other considered scan strategies.

Governing Equation

Heat Transfer Equations

Given an initial physical domain \(\varOmega \subset {\mathbb {R}}^3\) and a material following Fourier’s law of thermal heat conduction, we can model an LPBF AM process by means of the temperature-based heat transfer equations as follows [30]:

$$\begin{aligned} \rho c_p {\dot{T}}-\nabla \cdot \left( k \nabla T \right)&=Q&\text {in }\varOmega , \end{aligned}$$
(1)

under the following initial and boundary conditions:

$$\begin{aligned} k \nabla T&=q&\hbox { on}\ \partial \varOmega , \end{aligned}$$
(2)
$$\begin{aligned} T&=T_0&\text {at }t=0, \end{aligned}$$
(3)

with \(\rho \) indicating the constant material density, \(c_p=c_p(T)\) the temperature-dependent specific heat capacity, T the temperature field, \(k=k(T)\) the temperature-dependent thermal conductivity, Q the rate of heat per unit volume, q the heat flux prescribed on the domain boundaries \(\partial \varOmega \), and \(T_0\) the initial temperature.

The heat source input Q is modeled using a simple volumetric Gaussian heat source [31], such as:

$$\begin{aligned} \begin{aligned}&Q(x,y,z,t)=\frac{6\sqrt{3} P \eta }{\pi \sqrt{\pi } r^2 d}\exp \left( -3\left( \dfrac{(x-x_c)^2}{r^2}+\dfrac{(y-y_c)^2}{r^2} +\dfrac{(z-z_c)^2}{d^2}\right) \right) , \end{aligned} \end{aligned}$$
(4)

with P the laser power, \(\eta \) the absorptivity of the material, r the laser beam radius, d the depth of the melt pool, and with the laser beam centered in \(\left[ x_c, y_c, z_c\right] \).

The heat flux term includes radiation and convection heat losses. The heat loss due to a radiation flux \(q_\mathrm{rad}\) on the upper surface is modeled using the Stefan–Boltzmann law as follows:

$$\begin{aligned} q_\mathrm{rad}=\epsilon \sigma _{sb}(T^4-T_{a}^4), \end{aligned}$$
(5)

where \(\epsilon \) is the emissivity of the material, \(\sigma _{sb}\) the Stefan–Boltzmann constant, and \(T_a=T_0\) the ambient temperature. Newton’s law defines the heat loss by convection \(q_\mathrm{conv}\) on the upper surface of the domain as follows:

$$\begin{aligned} q_\mathrm{conv}=h(T-T_{a}), \end{aligned}$$
(6)

where h is the convective heat transfer coefficient.

Material phase-change is neglected in this model, since we do not include any latent heat term in Eq. 1. This choice is justified by the fact that latent heat has practically no influence on the quantities of interest for the present study as also demonstrated in the literature (see, e.g., [23]).

Mechanical Problem

In this work, we assume a thermo-elasto-plastic model where the mechanical equilibrium equation is written as follows:

$$\begin{aligned} \nabla \cdot {{\varvec{\sigma }}}={\mathbf {0}} \end{aligned}$$
(7)

with \({{\varvec{\sigma }}}\) the Cauchy stress tensor defined as:

$$\begin{aligned} {{\varvec{\sigma }}}={\mathbf {D}}^e{{\varvec{\varepsilon }}^e}, \end{aligned}$$
(8)

where \({\mathbf {D}}^e\) is the isotropic elasticity tensor and \({{\varvec{\varepsilon }}^e}\) the elastic strain. The total strain in the material \({\varvec{\varepsilon }}\) is written as the sum of elastic (\({{\varvec{\varepsilon }}^{e}}\)), thermal (\({{\varvec{\varepsilon }}^{th}}\)), and plastic (\({{\varvec{\varepsilon }}^p}\)) strains:

$$\begin{aligned} {{\varvec{\varepsilon }}}={{\varvec{\varepsilon }}^{th}}+ {{\varvec{\varepsilon }}^e}+{{\varvec{\varepsilon }}^p} \end{aligned}$$
(9)

The thermal component of the strain acts as a thermal load, driving the stress state evolution during the process and it is defined as:

$$\begin{aligned} {{\varvec{\varepsilon }}^{th}}=\alpha \varDelta T{\mathbf {I}}, \end{aligned}$$
(10)

where \(\alpha =\alpha (T)\) is the coefficient of thermal expansion (CoE) and \({\mathbf {I}}\) is the second-order identity tensor. The von Mises stress criterion is used in combination with the associated Prandtl–Reuss flow for small strains. The yield function \({\varPhi }\) and the plastic strain rate \({\dot{\varvec{\varepsilon }}}^{p}\) are then defined as:

$$\begin{aligned}&{\varPhi }= \sigma _{vm}-\sigma _y(T) \le 0, \end{aligned}$$
(11)
$$\begin{aligned}&\sigma _{vm}= \sqrt{\dfrac{3}{2}{\mathbf {s}}:{\mathbf {s}}}, \end{aligned}$$
(12)
$$\begin{aligned}&{\varvec{{\dot{\varepsilon }}}^p}= {{{\dot{\gamma }}}}\dfrac{\partial \varPhi }{\partial {\varvec{\sigma }}}, \end{aligned}$$
(13)

where \(\sigma _{vm}\) is the equivalent von Mises stress, \(\sigma _y=\sigma _y(T)\) the temperature-dependent yield stress, \({\mathbf {s}}=\varvec{\sigma }-1/3(\text {tr}\varvec{\sigma }){\mathbf {I}}\) the deviatoric stress tensor, and \(\gamma \) the equivalent plastic strain.

Mechanical problem is solved under the following boundary condition:

$$\begin{aligned} {\mathbf {u}}={\mathbf {0}} \end{aligned}$$
(14)

applied on the bottom surface of the bare plate.

Implementation of the Laser Control Strategy

The experimental data used in this work are taken from [4] to which we also refer for further details on experimental measurements. This set of measurements was conducted at the NIST laboratories on the Additive Manufacturing Metrology Testbed (AMMT), an open architecture LPBF system with custom laser control system specifically developed to study advanced monitoring and control strategies. NIST AMMT implements a jerk-limited motion control which minimizes the spatial and temporal error in the scan path to achieve a closer synchronization of laser power to position/speed. Such a jerk-limited motion control enables the different laser control modes we describe below.

G-code Control Modes

Laser scan paths are implemented on the AMMT by means of a modified numerical control (NC) protocol, or AM G-code, for LPBF. While the G-code provides nominal path, scan speed, and laser power, the nuanced control is defined in the G-code interpreter, which enables the three path modes and three laser power modes. The path modes primarily control the acceleration of the laser spot and laser on/off timing. The power modes primarily control the scaling of the laser power within each scan track (i.e., constant or variable). The interpreter then provides a direct laser-galvo digital command, based on the xy2-100 protocol. The machine parameters are listed in Table 1.

Table 2 reports an example of several lines of the xy2-100 based command, where each row is executed by the AMMT every 10 \(\mu \)s. It allows to vary the laser power value from one position to the next one. Table 3 lists the three different laser power control modes: constant power, constant power density, defined as the power/speed ratio, and thermal adjusted, and the three laser path modes: exact stop, continuous, and constant build speed. For a detailed definition of these six control modes, we refer to [32]. Combining these six different modes, we can have a full control of the power-velocity-position strategy. Furthermore, the digital command of Table 2 can provide direct input for the thermal simulation.

Table 1 Process parameters used in [4]
Full size table
Table 2 Example of extended G-code file
Full size table
Table 3 Laser path and power modes from [4]
Full size table

Laser Scan Strategy Comparison

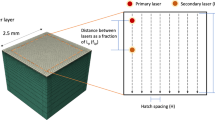
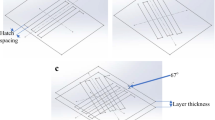
A set of 9 different scan strategies is considered. Rectangular areas of 2 mm \(\times \) 1.5 mm are filled by a pattern with hatch space of 0.2 mm and \(45^{\circ }\) inclination angle. The laser scan pattern is composed by four contour scan tracks defining the perimeter of the rectangle and 11 hatching patterns which fill the internal area. Figures 1 and 2 represent the laser power and speed values during the experiment. Such a set of scan strategies is obtained by a combination of the three different laser path and laser power control modes as reported in [4] (Table 4).

Table 4 Combinations of laser path and power modes in the 9 scan strategies from [4]
Full size table
Fig. 1
figure 1

Laser scan strategies obtained combining the three laser path and power modes. Laser power is represented by color [4]

Full size image
Fig. 2
figure 2

Laser scan strategies obtained combining the three laser path and power modes. Laser speed is represented by color [4]

Full size image

Numerical Implementation

In this section, we describe the finite element implementation of the thermo-mechanical model defined in “Governing Equation” section. The model is implemented in AdhoC++ an in-house finite element framework continuously developed and maintained at the Technical University of Munich (TUM) [33].

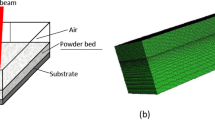
We employ a uniform finite element discretization with 25,000 Hex-8 elements with an element length of \(50\,\mu \hbox {m}\) and 23,001 nodes, this choice is made after a convergence study to obtain the best compromise between computational efficiency and accuracy. More details on spatial convergence for thermal problems with localized moving heat sources can be found in [33]. In Fig. 3, the problem domain and the corresponding thermal and mechanical boundary conditions used for the finite element analysis are depicted.

Fig. 3
figure 3

Problem domain and boundary conditions. Dimensions are in mm

Full size image

The temperature-dependent thermal and mechanical material properties are taken from [34] and reported in Tables 5 and 6, respectively. We assume a constant density of \(8440\, [kg/m^3]\) and a constant emissivity \(\epsilon =0.47\), while the absorptivity of the material is set to a constant value equal to 0.34 after calibration as described in a previous contribution of the authors [15].

In this work, we adopt a Backward Euler time integration scheme computing a time step every 10 entries of the AMMT digital command file for a positive (\(>0\)) laser power value and every 100 entries otherwise. Therefore, we employ a time step size of \(100\,\mu \)s during the active phase of the laser path and \(1000\,\mu \)s when the laser is switched off.

Table 5 Temperature-dependent thermal properties of the material IN625 [34]
Full size table
Table 6 Temperature-dependent mechanical properties of the material IN625 [34]
Full size table

Results and Discussion

In this section, we discuss the numerical results obtained employing the previously described numerical implementation. A validation of the thermal model is presented first in “Thermal Model Validation” section. The simulated melt pool area is compared to the one experimentally measured in [4] for the laser scan strategy 1. In “Effects of Control Strategies on Residual Stresses” section, the residual von Mises stresses for the nine different scan strategies are presented and the influence of the different control strategies on residual stresses is discussed. The proposed methodology allows us to be confident in the accuracy of the thermal model and consequently on the residual stress distribution, whereas residual stress magnitude will depend also on the mechanical model, which is not validated yet. Therefore, we expect the real stress magnitude to be within an order of magnitude but the prediction on the stress distribution be more accurate.

Thermal Model Validation

Using high-speed thermal camera data, it is possible to measure the melt pool area summing up the number of pixels with an intensity digital level (DL) above a calibrated threshold value. The threshold value adopted in both [4] and in the present work is 170 DL (of 256, or 8-bit dynamic range), obtained through a calibration process based on ex situ melt pool width measurements of a single laser scan track via microscope inspection using the same camera parameters (gain and integration time) as in [4].

Figure 4 reports the measured and the simulated melt pool area. The latter is evaluated measuring the area defined by a contour line for the melting temperature (\(T_m=1290\,^{\circ }C\)) in ParaView®. With the exception of the initial transitory, the simulated melt pool area at steady state closely resembles the measured values in both the four contour scan tracks and the eleven hatching patterns filling the internal region. Such a good agreement between simulated and measured melt pool area values makes us confident on the adopted thermal parameters chosen for modeling the thermal problem. In the literature (see, e.g., [11, 35]) thermal model validations are usually based on melt pool width measurements. Therefore, our validation using melt pool area measurements make us confident on the reliability of the presented residual stress distribution, whereas, as previously discussed, residual stress magnitude can be only qualitatively studied for the considered length scale.

In order to better understand the origin of melt pool area overshoots observed in Fig. 4, we re-computed the contour scan path using a much (\(\times 10\)) smaller time step, namely \(10\,\mu \)s for the active laser phase and \(100\,\mu \)s for the inactive one. These results are reported in Fig. 5 and clearly indicate that the overestimated melt pool area in the very initial portion of the contour tracks is due to the adopted time integration. Nevertheless, since this error occurs only in a very small time interval, it has almost no influence on the predicted residual stresses after cooling, whereas the computational cost increases dramatically. Therefore, we decide to accept this numerical error in our analysis.

Fig. 4
figure 4

Measured vs simulated melt pool area for laser scan strategy 1

Full size image
Fig. 5
figure 5

Measured vs simulated melt pool area for contour scan path of strategy 1 using a refined time integration

Full size image

Effects of Control Strategies on Residual Stresses

Table 7 Maximum residual stress (RS) magnitude on the scanned area for each scan strategy
Full size table

As stated in [2], the scan path mainly drives the distribution of residual stresses while direct changes to the energy input affect the residual stress magnitude. Since all the considered laser scan strategies follow an identical laser scan path, the residual stress magnitude is our primary quantity of interest to assess the influence of different control modes on residual stresses (Fig. 6).

Fig. 6
figure 6

Residual stress magnitude in MPa for the nine different laser scan strategies (Upper surface view)

Full size image

In Table 7, the maximum residual stress magnitude on the upper surface of each scan pad is reported. From these numerical results, we distinguish two main groups:

  • Group 1: It includes the scan strategies 2,3,5,7, and 8, where the maximum residual stress magnitude is between 242 MPa and 253 MPa. These strategies are characterized either by a constant power density (2,5, and 8) or by constant power and speed (3). For these scan strategies, the lower residual stress values can be explained due to the constant power and speed values. In [22], it is shown that increasing the laser power and decreasing the laser speed (i.e., higher energy input per unit volume) leads to higher residual stresses. Therefore, we could very likely expect that a lower, constant power density reduces the residual stress magnitude. The only exception seems to be case 7 for which we have not found a clear justification for the low predicted residual stress value.

  • Group 2: It includes all the remaining scan strategies not included in group 1 (1,4,6, and 9). The scan strategies of this group present higher residual stress values compared to the strategies in the first group. In fact, they are characterized by either thermal adjusted controls (1 and 4) or by constant power but sudden variations of laser speed (6 and 9), both effects lead to higher temperature gradients and consequently increase the residual stress magnitude. Another effect of the direct correlation between residual stress magnitude and thermal gradient [23, 36] is the higher values of residual stresses observed in the top-right corner of the pad, in particular, in 1 and 4. In fact, due to the lower temperature in the neighboring region obtained employing a thermal adjusted control strategy, the first hatches present a higher cooling rate whereas final hatches cool down slower.

Generally speaking, we can observe that constant power density seems to be the most effective control mode to decrease the residual stress magnitude, whereas no significant correlations between residual stresses and melt pool areas have been found in this study. The particular residual stress distribution in 9 is explained by the adopted control strategy. As depicted in Fig. 7a, the laser beam approaches the end point of the scan track with constant power, but, at the same time, the laser speed has to decrease for an increasing power density. This effect generates larger melt pool areas compared to the other strategies (see Fig. 7), explaining the peculiar stress distribution of this control strategy.

Fig. 7
figure 7

Temperature distribution comparison: scan strategy 9 vs 1

Full size image

Figures 8 and 9 show the longitudinal and transversal stresses along the laser scan direction in the hatching pattern, i.e., the two normal, in-plane stress components after rotating the stress tensor about the Z-axis by an angle of \(-45^{\circ }\), using the right-hand rule for rotation sign convention. We observe that the magnitude of these two stress components is similar and they are both in tension within the hatching region, whereas the boundary regions are almost stress free. This observation seems to confirm that larger scanning islands (i.e., longer scan tracks) lead to higher residual stresses as also recently demonstrated by Ali et al. [39] and by Ramos et al. [37]. The drawback of this solution is that the smaller the scanning island the higher the scan time. Moreover, most commercial machines use constant power/constant build speed strategy (also known as skywrite). The laser power needs to be turned on/off precisely at the boundary (while the laser is traveling at the very high nominal speed), or lack of fusion defects could develop along the boundaries. Smaller islands—and consequently shorter scan tracks—will promote the probability of such defects due to higher residual heat effect [38].

Fig. 8
figure 8

Hatching patterns longitudinal residual stress in MPa for the nine different laser scan strategies (Upper surface view)

Full size image
Fig. 9
figure 9

Hatching patterns transversal residual stress in MPa for the nine different laser scan strategies (Upper surface view)

Full size image

Conclusions

In the present work, a numerical finite element thermal model was first validated with respect to experimental measurements available in the literature and the associated coupled thermo-mechanical model was successively employed to quantify the influence on residual stresses of nine different combinations of scan speed and laser power control strategies. Numerical evidence shows that maintaining a constant power density is the most effective approach to limit residual stress magnitude. Moreover, this result provides a clear indication on the importance of an effective control strategy not only to avoid geometric defects but also to control residual stresses. Further research for the present work should include experimental validations of the presented thermo-mechanical finite element model, possibly employing more complex geometries and multilayer scan strategies.