FormalPara Key Summary Points

Why carry out this study?

It is still a challenge to determine the predictive accuracy of formula calculation in patients with long axial length (AL). There is an ever-growing demand for achieving an excellent binocular visual function in bilateral cataract patients with long AL.

The Cooke-modified AL (CMAL) methods showed high accuracy combined with Holladay 1 and SRK/T, but its benefits in other new formulas remain unknown, especially for patients with long AL. Of note, it remains unclear whether the CMAL methods can transfer to artificial intelligence (AI) formulas.

What was learned from the study?

We found that the AI-based Kane and PEARL-DGS with or without CMAL method could improve the refractive outcomes of the second eye in sequential bilateral cataract patients with long AL.

The Kane, PEARL-DGS, and BUII with specific correction factors displayed higher accuracy in bilateral cataract patients with long AL when the first eye suffered from refraction surprise.

Introduction

The incidence of myopia and high myopia is considerably high worldwide [1]. High myopia was reportedly associated with the earlier onset of cataracts [2, 3]. These patients with long AL usually require surgery much earlier than those with normal AL. In addition, their special refractive status often moves them to receive bilateral cataract surgery to get coordinated refraction [4].

Although the optical measurements and IOL power calculation have improved significantly, it is still a challenge to determine the predictive accuracy of formula calculation in patients with long AL [5,6,7,8]. For example, about 27% of patients with long AL exceed their targeted postoperative refraction by ± 0.50 D of the predictive value using new formulas, including BUII, Haigis, and Holladay 2 [7, 9,10,11]. Furthermore, in recent years, new-generation formulas based on AI technology were also applied to improve the predictive accuracy, including the Kane formula, Hill-radial basis function formula (Hill-RBF), and PEARL-DGS formula [12, 13]. In addition, the Cooke-modified AL (CMAL) methods showed high accuracy combined with Holladay 1 and SRK/T, but its benefits in other new formulas remain unknown, especially for patients with long AL [14].

Previous studies reported a correlation of prediction error (PE) between bilateral eyes [15,16,17]. In sequential bilateral cataract surgeries, the refractive outcomes of the first eye can be applied to improve the predictive accuracy of the second eye and the correction factors were calculated for the SRKII, SRK/T, Olsen, and others based on the ocular biometric measurements from A-mode ultrasound, partial coherence interferometry (PCI), and optical low-coherence reflectometry (Lenstar 900, Haag-Streit) devices [17,18,19]. The IOLMaster 700, a new-generation optical instrument based on the swept-source optical coherence tomography (SS-OCT) technique, has further improved the accuracy of biometric measurement. Besides, the SRKII and SRK/T are unsuitable for IOL power calculation in patients with long AL. Thus, with the widespread use of IOLMaster 700 and new formulas, particularly the BUII and Kane are applied to cataract patients with long AL, the specific correction factors based on the SS-OCT measurement need to be re-evaluated for optimizing the refractive outcomes.

In this retrospective study, to evaluate the optimal method for the refractive accuracy of the second eye in patients with long AL, we performed IOL power calculations using formula-specific factors for the BUII, Haigis, Holladay, Hoffer Q, SRK/T, and AI-based formulas, including the PEARL-DGS and Kane based on biometric measurements using IOLMaster 700 with swept-SS-OCT technique [20]. In addition, the CMAL methods were also included in this study to optimize the predictive accuracy of the second eye when the first eye suffered from refraction surprise.

Methods

Patients

We reviewed long AL cataract patients (AL ≥ 24.5 mm) who underwent sequential bilateral cataract phacoemulsification surgery by the same senior surgeon (X.L) from January 2019 to July 2021 at Zhongshan Ophthalmic Center, Guangzhou, China. Three types of hydrophobic acrylic IOL [MX60 (Bausch & Lomb), ZCB00 (Abbott Medical Optics), and Sensar AR40 (Abbott Medical Optics)] were used. The proportions of the three types of IOL were 23.47%, 72.45%, and 4.08% for MX60, ZCB00, and Sensar AR40, respectively. The inclusion criteria were as follows: patients who underwent uneventful cataract surgery and had stable refraction results (≥ 1 month) after surgery; patients with corneal opacity, ocular trauma, glaucoma, uveitis, retinal diseases, anisometropia, and postoperative best-corrected distance visual acuity worse than 20/40 were excluded. The study conformed to the Declaration of Helsinki. Meanwhile, it was approved by the Institutional Review Board/Ethics Committee of Zhongshan Ophthalmic Center, Sun Yat-sen University (2021KYPJ176). The requirement for informed consent was waived because only the patients' medical records were involved.

Biometry and IOL Power Calculation

Preoperative ocular parameters were obtained using IOLMaster 700 (1.88, Carl Zeiss, Germany). To study the accuracy of various formulas on an equal basis, IOL power calculations were investigated using optimized constants in the User Group for Laser Interference Biometry (ULIB) website (www.ocusoft.de/ulib/c1.html) [21]. In this study, we employ the BUII formula to calculate the IOL power before IOL implantation. The subgroups were analyzed based on different ALs (24.5 mm ≤ AL < 28.0 mm and AL ≥ 28.0 mm). Calculations of BUII were performed using the online calculator (http://calc.apacrs.org/barrett_universal2105/). The Kane used theoretical optics combined with the AI components [22]. The Pearl-DGS emerged recently, using AI and output linearization [13]. The IOL power of the Kane and PEARL-DGS formula was calculated using the online calculators (https://www.iolformula.com/ and https://iolsolver.com/, respectively). The second-eye IOL power was calculated by formula-specific factors, AI formulas, and the CMAL methods when the first eye suffered from refraction surprise (> 0.50 D). Mean absolute error (MAE), median absolute error (MedAE), and the proportion of PE within ± 0.25, ± 0.50, ± 0.75, and ± 1.00 D of each formula were compared. CMAL = 1.23853 + 0.95855 × traditional AL − 0.05467 × LT [14].

Formula-Specific Correction Factor Calculation

The dataset was divided into the first-eye and second-eye group in the current study. The PE was defined as the difference between predicted refraction and the postoperative spherical equivalent refraction. The regression coefficients were defined as the specific correction factors for eight commonly used formulas (Kane, BUII, PEARL-DGS, Holladay 2, Holladay 1, Haigis, Hoffer Q, and SRK/T) to refine the second-eye PE (PE2) based on the PE of the first eye (PE1). The regression coefficients were calculated by linear regression analysis of interocular PE according to Olsen’s approach [15]. The standardized regression analysis could provide the formula as:

$$ {\text{PE}}_{{{\text{cor2}}}} = ({\text{PE}}_{1} *{\text{regression coefficients}}) \, + {\text{ PE}}_{2} $$

In this study, the PEcor2 is the corrected PE of the second eye. The PE1 is the PE of the first eye, and the PE2 is the uncorrected PE of the second eye. When the regression coefficients, also the specific correction factors, were calculated from this formula, they could be applied to adjust the IOL power on the second eye in clinical practice. In this study, all the 196 eyes of 98 cataract patients who underwent sequential bilateral cataract phacoemulsification surgery were eligible for the regression model.

Statistical Analysis

The Wilcoxon signed-rank test was conducted to assess whether the mean refractive prediction error (ME) value differed from zero. Linear regression analysis was performed for the interocular correlation. Because the absolute PE was not normally distributed, the comparison of MedAE and MAE employed a nonparametric Friedman test with the Wilcoxon signed-rank post hoc test. The Pearson correlation coefficients were applied to evaluate the relationship between data meeting the normal distribution. Bonferroni correction was performed for multiple analyses. P < 0.05 was considered statistically significant. The analysis was carried out using SPSS (version 26.0, New York, USA).

Results

Characteristics of Participants

We enrolled 196 eyes of 98 patients (mean age: 58.7 ± 11.6 years; male: 58). Their preoperative biometric parameters are shown in Table 1. There was a robust interocular correlation of preoperative biometric parameters for bilateral AL, keratometry (flat, steep), anterior chamber depth (ACD), lens thickness (LT), central corneal thickness (CCT), and cornea diameter (CD) (R = 0.932, 0.961, 0.948, 0.947, 0.956, 0.924, and 0.836, respectively). R value is the correlation coefficient of bilateral biometric data (P < 0.001) (Table 1).

Table 1 Ocular biometric characteristics of participants (n = 98)
Full size table

The Kane Displayed the Highest Accuracy Compared with Other Formulas in the First Eye of Cataract Patients with Long AL

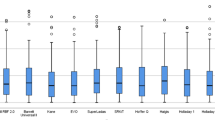
The refractive outcomes of commonly used IOL formulas for the first eyes are shown in Table 2 (n = 98). The Kane displayed the lowest MedAE (0.29D) and the highest proportion of PE within ± 0.25 (43.86%), ± 0.50 (82.81%), ± 0.75 (91.55%), and ± 1.00 D (97.22%) (Table 2, Fig. 1). When using BUII, the MedAE was 0.32 D, and the proportion of PE within ± 0.50 D was 76.53%. The Holladay 1 showed the highest MedAE value (0.55 D), and the SRK/T presented the lowest proportion of PE within ± 0.25 D (30.35%).

Table 2 Refractive outcomes of different formulas in the first eyes (n = 98)
Full size table
Fig. 1
figure 1

Stacked histogram showing the percentages of the first eyes within ± 0.25, ± 0.50, ± 0.75, ± 1.00, and >  ± 1.00 D of the prediction error for the entire dataset. BUII Barrett Universal II; D diopter

Full size image

In addition, subgroup analyses of MAE and MedAE values according to different ALs are shown in Table S1 in the electronic supplementary material. The Kane still showed the highest accuracy in the subgroup analysis of different ALs (24.5 mm ≤ AL < 28.0 mm and AL ≥ 28.0 mm).

A Significant Correlation for PE was Observed between Bilateral Eyes and the Coefficients were Formula-Specific

A significant positive correlation was observed between the PE of bilateral eyes for all the formulas, including the Kane, BUII, PEARL-DGS, Holladay 2, Holladay 1, Haigis, Hoffer Q, and SRK/T. The correction factors of different formulas were 0.250, 0.331, 0.343, 0.394, 0.409, 0.452, 0.503, and 0.520 for the Kane, BUII, PEARL-DGS, Holladay 2, Holladay 1, Haigis, Hoffer Q, and SRK/T, respectively. R-value is the regression coefficient between bilateral PE (P < 0.001) (Table 3). Figure 2 demonstrates the scatter plots of the PE of bilateral eyes.

Table 3 Correlation of the PE between bilateral eyes by different formulas (n = 98)
Full size table
Fig. 2
figure 2

Graphs showing the interocular correlation of the prediction error with different formulas for the entire dataset. A Kane formula (regression coefficient R = 0.250; P < 0.001); B BUII formula (regression coefficient R = 0.331; P < 0.001); C PEARL-DGS formula (regression coefficient R = 0.343; P < 0.001); D Holladay 2 formula (regression coefficient R = 0.394; P < 0.001); E Holladay 1 formula (regression coefficient R = 0.409; P < 0.001); F Haigis formula (regression coefficient R = 0.452; P < 0.001); G Hoffer Q formula (regression coefficient R = 0.503; P < 0.001); H SRK/T formula (regression coefficient R = 0.520; P < 0.001). Statistically significant (P < 0.05)

Full size image

The Kane, BUII, and PEARL-DGS with Specific Correction Factors Displayed Higher Accuracy as Compared with Other Two Methods

The second-eye IOL power was calculated using three different methods: formula-specific factors, AI formulas (PEARL-DGS and Kane), and the CMAL methods when the PE of the first eye exceeded 0.50 D with BUII. Concerning the AI formulas, the Kane showed a lower MedAE (0.73 D) compared with PEARL-DGS (0.80 D) for the second eye. The Kane also displayed a higher second-eye PE percentage within the ± 0.50, ± 0.75, and ± 1.00 D (48.15%, 74.07%, 88.89%, respectively) than those using PEARL-DGS (Figs. 3, 4 and Table 4).

Fig. 3
figure 3

Stacked histogram showing the percentages of the second eyes of the prediction error within ± 0.25, ± 0.50, ± 0.75, ± 1.00, and >  ± 1.00 D when the first eyes suffered from refraction surprise. aSEPE-Kane adjusted second-eye prediction error with Kane, aSEPE BUII adjusted second-eye prediction error with BUII, aSEPE-DGS adjusted second eye prediction error with PEARL-DGS, Kane-CMAL Kane with CMAL adjustment, BUII-CMAL BUII with CMAL adjustment, DGS-CMAL PEARL-DGS with CMAL adjustment

Full size image
Fig. 4
figure 4

Standard graphs showing the median absolute errors of the second eyes when the first eyes suffered from refraction surprise. aSEPE-Kane adjusted second-eye prediction error with Kane, aSEPE-BUII adjusted second-eye prediction error with BUII, aSEPE-DGS adjusted second-eye prediction error with PEARL-DGS, Kane-CMAL Kane with CMAL adjustment, BUII-CMAL BUII with CMAL adjustment, DGS-CMAL PEARL-DGS with CMAL adjustment

Full size image
Table 4 Refractive outcomes of second eyes when the first eyes suffered from refraction surprise (n = 23)
Full size table

Formula-specific factors of Kane, BUII, and PEARL-DGS (0.250, 0.331, and 0.343, respectively) applied to the second eye had a significantly lower MedAE (0.29, 0.30, and 0.34 D, respectively) than the MedAE without refinement (0.73, 0.88, and 0.80 D, respectively) (P < 0.001), and the percentage of second eyes within ± 0.50, ± 0.75, and ± 1.00 D significantly increased (Figs. 3, 4 and Table 4). These results suggested that the formula-specific factors used in the second eye could further reduce the MedAE, particularly for Kane, BUII, and PEARL-DGS.

The CMAL methods also reduced the MedAE of Kane, BUII, and PEARL-DGS formula. Kane-CMAL showed the lowest MedAE (0.63 D) compared with BUII-CMAL (0.64 D) and PEARL-DGS-CMAL (0.69 D). The Kane-CMAL displayed the highest proportion of PE within ± 0.25 and ± 0.50 D (25.00%, 53.57%, respectively) compared with BUII-CMAL and PEARL-DGS-CMAL (Figs. 3, 4 and Table 4).

In addition, subgroup analyses of MAE and MedAE values according to different ALs are shown in Table S2 in the electronic supplementary material. The formula-specific refinement still showed the highest accuracy in the subgroup analysis of different ALs (24.5 mm ≤ AL < 28.0 mm and AL ≥ 28.0 mm) (P < 0.001). Together, the Kane, BUII, and PEARL-DGS with specific correction factors showed significantly higher accuracy than two new AI-based formulas with or without the CMAL methods.

Discussion

Bilateral cataract patients with long AL generally undergo second-eye surgery shortly to achieve an excellent binocular visual function [4]. There is an ever-growing demand for better refractive outcomes in bilateral surgeries. Our study compared the effectiveness for reducing the PE of the second eye using formula-specific factors, AI-based formulas, and the CMAL methods in patients with long AL using IOLMaster 700. The results showed that the correction factors of the second eye with long AL are formula-specific. The Kane, BUII, and PEARL-DGS formulas with specific correction factors displayed higher accuracy compared with other methods. In clinic, we could utilize these specific correction factors to adjust the IOL power on the second eye. For example, the second-eye refraction can be calculated by subtracting a specific proportion of PE1 (PE1 * β) from the predicted refraction of the second eye.

There are different methods to reduce the PE of the second eye when the first-eye PE exceeded 0.50 D in patients with long AL. The segmented AL (sum of segment AL) is performed by various refractive indexes (RIs) separately for different ocular segments, and the CMAL approximates to the segmented AL [23, 24]. Cooke et al. showed that the CMAL methods improved the predictive accuracy of the Hoffer Q, Holladay 1, SRK/T, and Holladay 2 [14]. Nevertheless, it remains unclear whether it can be applied to other formulas. The findings in this study for the first time indicated that the CMAL methods also improved the accuracy of the Kane, BUII, and PEARL-DGS formulas for patients with long AL when the first-eye PE exceeded 0.50 D. The Kane has been developed using theoretical optics and AI components to improve the accuracy of IOL power calculation [22]. An update on IOL power calculation indicated that the Kane was more accurate for eyes with short, medium, and long AL than Hill-RBF (2.0) and EVO [12, 25, 26]. The PEARL-DGS is a new AI-based formula using the python toolbox and linear algorithms based on a standardized and open-source methodology of theoretical internal lens position (TILP) prediction, which is suitable for long AL [27]. This study also found that the Kane had a lower median absolute error and displayed a higher accuracy compared with other formulas.

The previous study reported that the correction factors were 0.56, 0.38, and 0.27, respectively, for the SRKII, SRK/T, and Olsen based on the biometric measurements from A-mode ultrasound or PCI for the entire AL spectrum [15]. Turnbull et al. also found that the correction factors vary according to several formulas with optical low-coherence reflectometry and IOLMaster 500 [18]. Klein et al. developed a polynomial regression formula, WeOptimeye2nd (WO2nd), to improve second-eye refractive outcomes especially in patients with extreme AL using IOLMaster 500 or Lenstar 900 [28]. It is known that the new generation formulas such as BUII and Kane have been extensively used for patients with long AL in clinical practice. Furthermore, the SS-OCT is becoming the golden standard for biometric measurements, especially in advanced cataract patients with long AL [20]. It uses an infrared swept-source light with the wavelength of 1055 nm, which obtains an axial resolution of 22 μm for 2000 A-scans/s [20]. This study showed a robust inter-ocular correlation of the ocular biometric parameters using IOLMaster 700 with the SS-OCT technique. Meanwhile, there is also a significant positive bilateral correlation of PE in patients with long AL, in which the correlation coefficients were re-calculated by regression analysis with eight commonly used formulas. The result revealed that the formula-specific correction factors were 0.250, 0.331 and 0.343 for the Kane, BUII, and PEARL-DGS, respectively, which exhibited the most accurate prediction accuracy of postoperative refraction in patients with long AL.

Recent studies suggested that the failures in measurements of axial length, keratometry, and ACD are usually associated with refractive surprise. Of note, the ACD is the most frequent error in IOL power calculation and the refractive surprise. Actually, the prediction of the postoperative ACD is still the major obstacle in accurate IOL power calculation despite the improved optical measurements and IOL formulas [29, 30]. Some modern IOL formulas would use various biometric variables to improve the predictive accuracy [31, 32]. For example, Li et al. applied the machine learning (ML) methods to improve the refractive prediction performance of postoperative ACD and demonstrate that the ML method can improve the predictive accuracy of Haigis, Hoffer Q, Holladay 1, and SRK/T formulas [33]. Studies attributed 35.5% of non-systematic predictive errors to the effective lens position (ELP), and the refinement of the second-eye PE may be attributable to the revision of remaining errors from the ELP and the inter-ocular symmetry to some extent [15, 18]. Although several new formulas used more biometric variables or optical parameters such as LT and CD to predicate the ELP, the accurate prediction of the ELP remains the major obstacle in formula calculation, particularly in cataract patients with long AL [34, 35].

There are some limitations to this study. One is that we evaluated the formula-specific factors based on biometric measurement from IOLMaster 700. The specific correction factors in this study may not apply to the other optical instrument such as the Lenstar 900 (Haag-Streit AG, Koniz, Switzerland). Another limitation is that three types of IOLs were utilized in this study which could affect the PE. Further prospective studies with large sample sizes using the same type of IOL are still required to validate the results. In addition, the latest PEARL-DGS calculator provides experimental postoperative contralateral eye information and posterior corneal radius to predict the lens position [27]. Calculations using the data of the first operated eye by PEARL-DGS are experimental and optional (https://news.iolsolver.com//informations/). In this study, we used the standard mode of the PEARL-DGS calculator without the additional options of “Postoperative Contralateral Eye Informations” and “Posterior Corneal Radius.” Further research in this field is still needed.

In summary, the formula-specific refinement has a positive effect on reducing the PE of the second eye. The other advantages include that it does not require complicated calculations and is suitable for many commonly used formulas. Meanwhile, the formula-specific refinement simultaneously considers some system errors derived from the ELP and others in eyes with long AL. Therefore, formula-specific correction factors currently represent an appropriate method to optimize the refractive outcomes of the second eye when the first eye suffered from refraction surprise in sequential bilateral cataract patients with long AL. Nevertheless, using formula-specific correction factors to optimize the refractive outcomes simply introduces an adjustment method based on the correlation of bilateral PE, which is not suitable for patients with abnormal ocular biometric parameters. Undoubtedly, developing more accurate biometric measurement technology and exploring new methods to predict the ELP accurately are still needed to improve the accuracy of formula calculations.

Conclusions

Our findings showed that the new AI-based Kane and PEARL-DGS with or without the CMAL method could improve the refractive outcomes of the second eye in sequential bilateral cataract patients with long AL when the first eye suffered from refraction surprise. The Kane, PEARL-DGS, and BUII with specific correction factors displayed higher accuracy.