Introduction

Pile foundations have become an inevitable foundation choice in regions where geotechnical conditions at shallow depth are inadequate for the structural loads. Built structures can be subjected to dynamic loads acting on the superstructure, as well as seismic loads acting on the foundation-soil system. Piles as structural elements act as links that transfer the static and dynamic loads between the structure and the geologic medium. Ever since the advent of power computational tools for soil-structure interaction analyses in the late 1970’s, the problem of a vibrating pile embedded in a halfspace has received considerable research attention. The response of a pile to a dynamic load is known to be dependent on the intensity as well as the frequency of excitation.

Computation of lateral dynamic stiffness of pile forms an important stage in the design of foundations systems that are subjected to dynamic loads. This is particularly true in the case of machine foundations where lateral dynamic loads can be prominent. Based on the methodology, the analysis techniques can be classified as semi analytical, Winkler based formulations, rigorous three-dimensional continuum-based methods, and numerical methods. One of the earliest attempts to solve the problem of horizontally vibrating end bearing pile was made by Tajimi [1] whereby a linear viscoelastic Kelvin-Voigt soil model was adopted to model the soil stratum. A more rigorous solution was proposed by [2] and [3] for vertical and horizontal vibrations, respectively. The approach was based on evaluating plane strain soil reactions accounting for radiation damping in soils. Later on, Novak et al. [4] presented closed form solutions of dynamic pile response incorporating hysteretic damping of soils. Using the developed methodology, the researchers also presented stiffness and damping constants for single piles in homogeneous and parabolic soil profiles [4, 5].

The intricacies and computational costs of advanced numerical methods pose a challenge for structural engineers. The dynamic Winkler model for pile foundations can be considered as a quick alternative to complex analytical solutions. Makris and Gazetas [6] modelled the soil using continuously distributed frequency dependent linear springs and dashpots to estimate the later stiffness of piles. The dynamic Winkler model is robust in terms of its ability to account for soil layering and changes in pile geometry with length [7, 8]. Recently, new physics based derivations have led to expressions to estimate the soil spring and dashpot coefficients [9,10,11]. Another method developed for soil-structure interaction (SSI) problems is the cone method by Wolf et al. [12]. The method idealised a three dimensional halfspace into a truncated semi- infinite cone, thus overcoming the theoretical complexity of a three dimensional analysis. Jaya and Prasad [13] extended the method to solve the dynamic impedances for single and group piles embedded in layered soil stratum, which yielded good comparison with results from other analytical methods. Pal and Baidya [14] used the cone model to successfully predict the response of the experiment using scaled down large pile group reported by [15].

Rigorous three-dimensional continuum-based methods have primarily focused on axial and torsional vibration of piles in homogeneous and layered soil [16,17,18,19]. Several studies have also resulted in closed form expressions for lateral harmonic response of piles [20,21,22,23]. However, these methods are mathematically complex and most often not appeal to geotechnical engineers. Numerical analysis of the lateral dynamic response problem is however possible incorporating nonlinear material and interface behavior [24,25,26,27]. Numerical methods that use nonlinear constitutive models work in the time domain, wherein the governing differential equation is solved by time marching algorithms. Numerical methods based on the substructuring approach forms another category wherein computational efficiency is achieved by means of linear and equivalent linear approximations for material nonlinearity [28].

In situations where quick estimates of dynamic pile stiffness and natural frequency are needed, it becomes necessary to utilize data from routine site investigation reports and without advanced laboratory test data. This study investigates the applicability of two fast analysis methods for dynamic pile stiffness, namely the Flexible Volume Substructuring Method (FVSM) and the Beam on Dynamic Winkler Foundation (BDWF) method. A lateral dynamic load test carried out on a full-scale test pile in Hazira, India constructed for a machine foundation project is discussed. The details of the machine foundation and results from a numerical analyses on the stiffness and load sharing characteristics of the pile group, are discussed in [29]. The objective of this study, however, is to make blind predictions of the natural frequency of a single pile with various mathematical models, utilizing soil properties from a standard site investigation program.

Lateral Dynamic Load Test on a Full-Scale Pile

Background

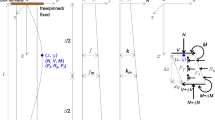
The pile foundation under consideration was designed to support a compressor unit in an Ethane cracker plant situated in Hazira, India. A schematic diagram showing the compressor, gear and motor units is shown in Fig. 1. The compressor had an operating frequency in the range 8200 to 10,770 rpm, and the allowable velocity at the foundation level was 2.5 mm/s. The compressor, motor and gear equipment weigh a total of 51.1 tonnes, and a baseplate of size 8.7 m × 3.8 m was designed to support it. Pile foundations were proposed for the site considering the weaker silty clay deposits in shallow depths. Details of the compressor unit can be found in [29]. Evaluating the pile stiffness is a crucial step in calculating the dynamic response of a machine-foundation system, as the startup and operation of the compressor unit would result in the foundation system crossing its resonant frequency. In this regard lateral dynamic load tests were proposed on test piles at a location adjacent to the proposed compressor foundation. Free and forced vibration tests were carried out in conformation with IS 9716:1981 [30]. The details of the load test on one of the piles along with the soil profile determined from the nearest borehole are presented in the following sections.

Fig. 1
figure 1

Illustration showing the compressor unit in plan and elevation

Full size image

Soil and Pile Properties

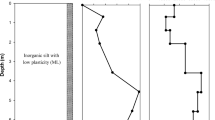
The soil profile at the site comprises of layers of silty clay and silty sand with relatively hard stratum occurring at a depth of 15–20 m. SPT and seismic cross hole tests were carried out in boreholes near the test pile, and the results are presented in Fig. 2a and b. The top 10 m comprised of layers of silty clay with SPT values ranging from 5 to 10. The soil shear modulus was found to vary from 25 to 47 MPa in the top 5 m of the profile. Hard sandy stratum with SPT N values of over 44 and shear moduli greater than 433 MPa was observed beyond a depth of 15 m. The ground water table was observed at a depth of around 1.5 m at the time of testing. Table 1 summarizes the soil layer characteristics at the site.

Fig. 2
figure 2

a Soil stratification, b shear wave velocity profile, c SPT N profile, and an illustration of the pile at the site

Full size image
Table 1 Soil properties at the site
Full size table

A bored cast in situ type pile foundation with four piles of diameter of 0.5 m and length of 18 m, each with a maximum vertical capacity of 750 kN was proposed to support the base plate. The test pile considered in this study was cast in the vicinity of the proposed foundation, with M35 grade concrete, conforming to IS 456 2000. The length to diameter ratio (L/d) of the pile was 36. To facilitate fixing of the oscillator, a pile cap of dimensions 0.75 m × 0.75 m × 0.75 m was cast on top of the pile. A gap of 20 mm was left below the bottom of the pile cap to the ground level. The flexural reinforcement of the pile consisted of ten T16 bars and its helical reinforcement consisted of T8 bars. Following the criteria suggested by [31, 32], the pile can be considered to be flexible for the soil profile at the site.

Test Setup and Procedure

The pile was subjected to free vibration test as well as a series of forced vibration tests. Conforming to IS 9716:1981 [30], the free vibration test was performed by the application of a lateral load followed by sudden release. The reaction load was provided by a second pile of the same dimensions constructed at a distance of 3 m from the test pile. The lateral load was applied by rotating a pulling screw, and the load was released using a clutch arrangement as shown in Fig. 3. Two tests were conducted on the same test pile. The free vibration response was then recorded using two uniaxial accelerometers attached to the pile cap at the pile cut off level. Signals from the accelerometers were amplified and recorded using a data acquisition system connected to a computer.

Fig. 3
figure 3

Illustration showing the free vibration test setup

Full size image

The forced vibration test was performed by attaching a Lazan type eccentric mass oscillator on the pile cap. This type of oscillator has been used in previous studies to drive soil-pile-mass systems [33,34,35,36,37,38]. The oscillator assembly together with the mild steel base plate weighed 113 kg in total. The oscillator was driven by a DC motor via a flexible shaft. An illustration showing the forced vibration test setup is presented in Fig. 4. The supply voltage to the DC motor was adjusted using a speed control unit and a tachometer was used to measure the rotational speed of the shaft. The force exerted by the oscillator was controlled by adjusting the phase angle between the two unbalanced masses mounted on counter rotating shafts. The oscillator was operated in the frequency range of 9 to 30 Hz for which the amplitude of force varied from 0.5 to 7.4 kN. The exciting force-frequency relationship for the oscillator is presented in Table 2. A photograph showing the oscillator assembly on the pile cap is presented in Fig. 5.

Fig. 4
figure 4

An illustration of the forced vibration test setup (inset shows reinforcement details of the pile)

Full size image
Table 2 Magnitude of quadratic excitation force from the oscillator
Full size table
Fig. 5
figure 5

Photograph showing the pile and oscillator assembly

Full size image

Mathematical Models

Beam on Dynamic Winkler Foundation Models

The modelling of pile as a Winkler foundation has been proven to be a quick and robust method to analyze dynamic soil-pile interaction [7, 39, 40]. The method can incorporate layered soil medium and varying pile geometry. In this method, the soil in each soil-pile segment is modelled as a continuously distributed frequency dependent linear springs (kxi) and dashpots (cxi). We consider a pile of length L, diameter d, modulus Ep in a generalized multilayered soil profile as shown in Fig. 6a. Let the ith layer have a modulus \({E}_{si}\), density \({\uprho }_{si}\), damping ratio \({\upbeta }_{i}\), and poisson’s ratio ν. Considering the equilibrium of an infinitesimal element of the pile having mass per unit length m in ith layer, as shown in Fig. 6b, we have

$$E_{p} I_{p} \frac{{d^{4} y\left( z \right)}}{{dz^{4} }} + \left( {k_{xi} + i\omega c_{xi} - m\omega^{2} } \right)y\left( z \right) = 0$$
(1)
Fig. 6
figure 6

a Illustration of the pile modelled as a beam on dynamic Winkler springs; b forces acting on a pile segment and c idealized SDOF system ignoring rotational and cross coupling stiffness

Full size image

Expressions for the stiffness and damping terms in Eq. (1), for various soil profiles have been the subject of several studies in the past. Analyses based on the theory of elasticity have established that the spring stiffness kxi can be expressed as a function of the soil Young’s modulus Es as [6, 31, 41,42,43]:

$$k_{x} = \delta E_{s}$$
(2)

For typical soil-pile systems, the value of the coefficient δ varies from 1.0 to 1.2 for free headed piles and 1.5 to 2.5 for fixed headed piles. Some of the earliest studies have represented the dashpot coefficient as the sum of a radiation damping term and a hysteretic damping term as [6, 40, 44]:

$$c_{x} = 6a_{o}^{ - 0.25} {\uprho }_{s} V_{s} d + 2{\upbeta }_{s} \frac{{k_{x} }}{{\upomega }}$$
(3)

where \(E_{s}\) is the Young’s modulus of the soil layer, \(\rho_{s}\) is the density of the soil layer, \(V_{s}\) is the shear wave velocity of the soil layer, and \(\beta_{s}\) is the damping ratio of the soil layer, and ao (defined as ωd/Vs) is the dimensionless frequency with \(\omega\) being the circular frequency of the applied lateral force.

More recent studies based on physics based modelling of soil-pile interaction problem have presented more accurate expressions for the spring and dashpot terms. Karatzia and Mylonakis [11] proposed the following expressions for linear soil shear modulus profile:

$$k_{x} = \delta E_{sd}$$
(4)
$$c_{x} = \pi \rho_{s} V_{s} d\left[ {0.25 + 0.8\frac{{V_{p} }}{{V_{s} }}} \right]a_{o}^{ - 0.4}$$
(5)

where Esd is the soil Young’s modulus at one pile diameter, δ = 2.449 (for free headed pile), Vp is the compression wave velocity. More recently, Anoyatis and Lemnitzer [9] proposed a simplified expression for the dynamic spring stiffness applicable to both kinematic and inertial interaction problems, as an alternative to mathematically complex formulations [10, 45]:

$$k^{*} = \frac{{4\pi \eta_{s}^{2} G_{s}^{*} }}{{\ln \left( {\eta_{s} } \right) + \left( {1 + \eta_{s}^{2} } \right)\left( {\ln \left( {2/s} \right) - \gamma } \right)}}$$
(6)

where \(G_{s}^{*}\) represents the shear modulus of the soil layer and the other variables are defined as:

$${\upgamma } \approx 0.577$$
(7)
$${\upeta }_{{\text{s}}} = \sqrt {\frac{{2\left( {1 - {\upnu }_{{\text{s}}} } \right)}}{{1 - 2{\upnu }_{{\text{s}}} }}}$$
(8)
$$s = 0.5\sqrt {a_{{{\text{cutoff}}}}^{{2}} - \frac{{a_{o}^{2} }}{{1 + 2i\beta_{s} }}}$$
(9)
$$a_{{{\text{cutoff}}}} = \frac{\pi d}{{2L}}$$
(10)

The expressions for soil springs and dashpots from the three methods listed above (Eqs. 3–10) were utilized in this study to develop three BDWF models. Solving the differential equation for each layer, we get

$$y\left( z \right) = e^{{{\uplambda }_{i} z}} \left( {A\sin \left( {{\uplambda }_{i} z} \right) + B\cos \left( {{\uplambda }_{i} z} \right)} \right) + e^{{ - {\uplambda }_{i} z}} \left( {C\sin \left( {{\uplambda }_{i} z} \right) + D\cos \left( {{\uplambda }_{i} z} \right)} \right)$$
(11)

where A, B, C, D are constants, z represents the vertical dimension local to each layer, and \({\uplambda }_{i}\) is given by

$$\lambda_{i} = \left( {\frac{{k_{xi} - m\omega^{2} + i\omega c_{xi} }}{{4E_{p} I_{p} }}} \right)^{1/4}$$
(12)

The state vector, representing the displacement, rotation, shear and moment at a point be given by

$$\left[ {\begin{array}{*{20}l} {y\left( z \right)} \hfill \\ {\Phi \left( z \right) = \frac{{{\text{d}}y}}{{{\text{d}}z}}} \hfill \\ {M\left( z \right) = E_{p} I_{p} \frac{{{\text{d}}^{2} y}}{{{\text{d}}z^{2} }}} \hfill \\ {Q\left( z \right) = E_{p} I_{p} \frac{{{\text{d}}^{3} y}}{{{\text{d}}z^{3} }}} \hfill \\ \end{array} } \right]$$
(13)

The transfer matrix approach adopted by [7] was employed as detailed in “Appendix”. After applying the relevant boundary conditions at the pile tip and head, the complex stiffness K of the pile soil system be evaluated as:

$$K = k + 2\beta kI$$
(14)

where the real part of K denotes the stiffness and \(\beta\) denotes the damping ratio of soil pile system.

An idealized model of the pile cap-pile-soil system was then adopted as shown in Fig. 6c. The equation of motion for the idealized single degree of freedom system was solved in the frequency domain to obtain the displacement at the center of gravity of the pile cap.

Numerical Modelling Using the FEM–BEM Method

In addition to the BDWF model, a numerical model was also developed to simulate the dynamic response of the pile in consideration. Coupled FEM–BEM formulations are known for their computational efficiency and have been employed by several researchers to study SSI problems with complex geometry [46,47,48]. The fundamental idea is to model the near field accurately while modelling the far-field using analytical solutions that are computationally faster. The FEM–BEM based ACS SASSI program [49] couples a three-dimensional finite element model of the foundation and near field soil with far-field soil modelled by the Thin Layer Method [50], and is adopted in this study. The Flexible Volume Substructuring Method (FVSM) reduces the dynamic stiffness of the structure by the corresponding properties of the excavated soil volume, which is retained within the horizontally layered halfspace and is the most accurate among the substructuring schemes [51]. The FVSM divides the soil-foundation-structure system into three subsystems and the equation of motion for a foundation vibration problem can be expressed as:

$$\left[ {\begin{array}{*{20}c} {X_{ii} - K_{ii}^{2} + K_{ii}^{3} } & {X_{iw} - K_{iw}^{2} } & {K_{is}^{3} } \\ {X_{wi} - K_{wi}^{2} } & {X_{ww} - K_{ww}^{2} } & 0 \\ {K_{si}^{3} } & 0 & {K_{ss}^{3} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{i} } \\ {u_{w} } \\ {u_{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P_{i} } \\ 0 \\ {P_{s} } \\ \end{array} } \right\}$$
(15)

where K, X, P and u represent dynamic stiffness matrix, the soil impedance matrix, the force vector, and the displacement vector respectively. The indices 2 and 3 denote the excavated soil volume and the structure respectively. The subscripts i, w and s represent the nodes at the soil-structure boundary, nodes within excavated soil and nodes on the structure respectively. In the SASSI methodology, the impedance matrix, X is developed from an axisymmetric model that consists of a single column of cylindrical elements with transmitting boundaries boundaries [52, 53]. The axisymmetric model is used to compute the force–displacement responses for all degrees of freedom of each node below the ground surface to construct the compliance matrix, which is then inverted to obtain the impedance matrix. The steps involved in this methodology follow the order i) solving the site response problem ii) solving the impedance problem and iii) assembly of complex stiffness matrices for the whole system and iv) solving equation of motion described in Eq. (15).

A 3D model was developed to simulate the free and forced vibration response of the single pile under investigation. The cube shaped pile cap was modeled using eight noded solid elements and was not in contact with the adjacent soil elements as in the field. The oscillator and its base pad are considered as point loads on the pile cap. The pile was modelled as a central beam connected by rigid links [54,55,56,57]. The central beam and rigid link technique involves the removal of soil elements from the volume occupied by the pile, and insertion of beam elements at the centre of the volume, which are connected horizontally to the soil nodes using rigid beam elements. More details on the theoretical framework and modelling can be found in [29, 58]. The soil properties described in Table 1 were assigned to the soil layers. The pile material behavior was assumed to be linear elastic with a Young’s modulus value of 29 GPa, Poisson’s ratio of 0.2 and a unit weight of 25 kN/m3. Meshing of the geometry was carried out restricting the maximum height of elements below one fifth of the maximum wavelength considered in the analysis [59, 60]. A cutaway section of the FE model showing the pile, pile cap and near field soil elements is presented in Fig. 7.

Fig. 7
figure 7

FE mesh model of the pile soil system

Full size image

The analysis stage in the FVSM methodology is essentially linear in nature. However, the equivalent linear approach can be used to approximate the strain dependent variation in soil stiffness and damping. The near field soil elements properties can be updated in this process. In this study, an iterative analysis was carried out whereby the octahedral shear strain in each of the eight noded near field soil elements from the previous step was used to compute the shear modulus and damping ratio for the next step [49]. The convergence in the equivalent linear technique was observed within an average of 4 iterations in this study.

The free vibration response of the pile was simulated by applying an impulse at the center of the vertical face of the pile cap. An impulse of 15 Ns was applied to produce a maximum displacement comparable to the displacement observed during the field test. The simulation of the forced vibration response was also carried out using the same model. The dynamic vertical force calculated based on the eccentricity and frequency was distributed on the nodes on the top of the pile cap. The displacement response at the node corresponding to the accelerometer location at the pile was then extracted in the post processing stage of the analysis.

Results and Discussion

Free Vibration

The free vibration response obtained from the two-field test are presented in Fig. 8a and b. The corresponding Fourier spectra are presented in Fig. 8c and d. The average damped natural frequency of the system from the two free vibration responses were found to be 19.01 Hz and the average damping ratio from the logarithmic decrement method was found to be 0.14. The numerical simulation produced a damped natural frequency of 18.18 Hz and a damping ratio of 0.120. For a clear picture of the estimation methods, we also computed the natural frequency using expressions for lateral pile reported in previous studies, with appropriate assumptions in the soil stiffness profile. The undamped natural frequency obtained from various methods are presented in Table. 3. The numerical simulation was found to produce a close estimate of the undamped natural frequency, with an underestimation of 4.36%. The BDWF methods produced a fair estimate of the natural frequency with errors depending on the calculation of soil spring stiffness and damping coefficients. The expressions proposed by [9] and [6] produced estimates with errors of 21.72% and 30.14% respectively, while the expressions proposed by [11] for a linear soil profile idealization, produced an error of 48.76%. The dependance of BDWF models on the assumed soil profile is evident. For a broader perspective, the natural frequency was also calculated using commonly used lateral pile stiffness formulae for a slender pile in linear inhomogeneous soil proposed by [40, 61,62,63,64] assuming a linear soil profile. However, these formulae resulted in large errors in the predicted natural frequency possibly due to the underlying assumptions in soil stiffness profile. The BDWF method, nevertheless, can be considered as one of the quickest methods considering the very short computation time, in tune of 2 s in a personal computer with 8 GB of primary memory.

Fig. 8
figure 8

a, b Time histories of free vibration response of the pile recorded at the pile cut off level and c, d corresponding Fourier spectra

Full size image
Table 3 Undamped natural frequency of the pile-soil system by various methods
Full size table

It is common practice that in the computation of pile impedances, the variation of the soil stiffness with depth or the stiffness profile is often idealized based on the available borelog, or geological data. A number of explicit closed form solutions are available for standard soil profiles where the stiffness profile can be expressed by convenient mathematical expressions [11, 65, 66]. To assess the change in the undamped natural frequency with the stiffness profile, an exercise was carried out using the BDWF model with Winkler expressions proposed by [9]. Three different soil profile idealizations were developed using the expression:

$$E_{s} = E_{sd} \left[ {\alpha + \left( {1 - \alpha } \right)\frac{z}{d}} \right]^{n}$$
(16)

where \(E_{s}\) represents the elastic modulus of soil at depth z, \(E_{sd}\) represent the modulus at one pile diameter, and \(\alpha\) and n are dimensionless inhomogeneity parameters. The three idealized profiles considered are: Profile 1 (α = 0.7, n = 0), Profile 2 (α = 0.55, n = 1) and Profile 3 (α = 0.9, n = 2.3). Figure 9a shows the three idealized profiles compared against the actual stiffness profile at the location. The pile stiffness (near zero frequency) was computed for various l/d ratios by varying the diameter of the pile. The change in normalized lateral pile stiffness with respect to the slenderness ratio is presented in Fig. 9b. It could be noted that the influence of slenderness ratio on the lateral pile stiffness is predominant at low slenderness ratios. The difference in estimated natural frequencies for the three idealized profiles are practically very less, as shown in Fig. 10. However, the three idealized profiles underestimated the natural frequency obtained using the actual soil profile by 6 to 6.6%.

Fig. 9
figure 9

a Variation of soil stiffness with depth and b normalized lateral pile stiffness against slenderness ratio

Full size image
Fig. 10
figure 10

Undamped natural frequency in different stiffness profiles

Full size image

Forced Vibration

The time histories of acceleration at the pile cut off level for the various excitation and frequency levels were sampled at 1200 Hz and recorded by the data acquisition system. The amplitude of vibration was then used to obtain the frequency response curves of the pile at various force intensity levels. Increasing force intensity level, denoted by the oscillator eccentricity level was found to increase the recorded acceleration amplitudes. Figure 11 shows the typical 5 s time windows of response obtained for the first eccentricity level (\(e={32}^{o}\)). The four different frequency response curves obtained from the field test as well as those obtained from the simulations are presented in Fig. 12a and b. The pile response obtained from the field test clearly exhibits characteristics of a nonlinear system, with the resonant frequency decreasing with increasing force intensity [67].

Fig. 11
figure 11

Time histories of steady state motion recorded at the pile cut off level for force level corresponding to \(e = 32.8^{^\circ }\)

Full size image
Fig. 12
figure 12

Comparison of forced vibration response of the pile: a experiment vs BDWF model and b experiment vs numerical model

Full size image

The BDWF analysis utilizing the soil spring and dashpot modelling from [10] was essentially linear in nature. As shown in Fig. 12a, the analysis produced a closer estimate of the frequency response curve at lower load intensity levels. Although the shift in resonant frequency was not captured, the amplitude of vibration at the lowest eccentricity level of the oscillator was captured with a fair degree of accuracy. The error in prediction of resonant frequency was found to increase with the force level reaching 24.56% at the highest eccentricity level of the oscillator. The numerical simulation utilizing the equivalent linear method was found to capture the resonant frequency with a fair degree of accuracy as shown in Fig. 12b. The decreasing resonant frequency with increasing intensity of loading due to nonlinear soil response was captured. However, the amplitude of vibration was overestimated at frequencies above 15 Hz. For example, the error in prediction of the peak amplitude at the highest eccentricity level of the oscillator was 33.18%. It must be noted that the strain dependent dynamic soil properties were not determined from laboratory analyses. The accuracy of the analysis is influenced by the modulus and damping curves assigned to the soil layers.

Conclusion

Lateral free and forced vibration tests were carried out on a full-scale instrumented pile in layered soil. A detailed site investigation was carried out to arrive at a shear wave velocity profile at the location, which was then used for blind predictions using two fast mathematical models. The numerical FVSM and BDWF methods were evaluated against the experimental results. The present investigation was focused on the simulation of the dynamic pile response using analysis techniques utilizing linear and equivalent linear soil modelling with soil properties inferred from a routine soil investigation program. Based on the results obtained from the study, the following conclusions can be drawn:

  • The BDWF method has been found to be reliable in producing a quick estimate of the natural frequency of the pile-soil system. However, the calculation of soil spring and dashpot coefficients plays an important role in the final estimate of pile impedance. The soil spring and dashpot coefficients proposed by [9] were found to produce the most accurate estimate of pile natural frequency. Idealized soil stiffness profiles were found to produce a reasonable estimate of the lateral pile stiffness.

  • The FVSM method with equivalent linear soil modelling was found to capture the nonlinear resonant frequency variation of the pile-soil system with a fair degree of accuracy. The equivalent linear methodology to account for strain dependent variation in soil stiffness and damping, as well the assumed modulus reduction curves of soil layers produced an overestimation of the forced vibration amplitude at higher frequency levels for all force intensity levels.

  • The BDWF method was found to produce a reliable estimate of the frequency response curve at low intensity of loading. Results from the present study suggest that this method can be effectively used as a primary estimate of natural frequency in lateral mode. However, Winkler methods with linear springs are unable to capture the variation in resonant frequency with force intensity.