Introduction

As regards the cover of non-hazardous municipal solid waste (MSW) landfills, the European Council Directive 1999/31/CE [1] imposes a biogas collection layer (BCL) thickness not less than 0.5 m and requires an adequate protection from clogging. This allows to avoid a geotechnical instability of capping, induced by the build-up of the biogas pressure below the mineral liner. For this reason, the granular material composing of BCL firstly has to satisfy the following retention and permeability criteria: (1) a grain size compatibility with adjacent layers must be achieved on the basis of the usual filter design criteria; (2) the internal self-stability (ISS) of the layer must be guaranteed through the absence of cementing minerals (such as limestones) and elongated grains (that could favor interlocking) and avoiding the migration of the finer particles; (3) the BCL must bear stresses induced by dynamic and static loads (weight of trucks and layers above the BCL) acting during the different phases of its life.

The main geotechnical properties of granular materials (stress–strain behaviour, shear strength, hydraulic conductivity) are related to maintaining the integrity of the grains over time. If grains breakage occurs, the finer fraction increases and the average hydraulic conductivity of BCL decreases; this could make the granular material no more suitable for the design purpose.

In the final multilayered cover, the BCL, located underneath the mineral liner, may be considered isolated from the external environment. Consequently, the use of solid wastes, with geotechnical behaviour similar to that of granular soils, may be considered as an environmental sustainable solution. The above-mentioned Council Directive does not prescribe in detail the materials to be employed in the BCL of a non-hazardous MSW landfill. For this reason, a general acceptance procedure of cullet, available on the waste market and capable of satisfying the design requirements, has been developed and proposed. Cullet is a mixture of different coloured glass fragments resulting from crushing of waste glass (predominately food containers and drink bottles) collected from different sources, and it seems to be a promising material as a substitute of natural granular soils. Previous studies have shown that cullet has been widely used in many construction applications in the USA, including general fill, base and sub-base for road works, drainage filters, landfill covers, etc. [2]. The Clean Washington Center [2, 3] carried out some studies, which indicated that cullet specimen, having maximum size of 19 mm, would have physical properties similar to those of natural granular materials, and consequently, cullet could be used as an alternative to conventional granular materials. In regard to its hydraulic conductivity k and fines migration, other studies showed that:

  • Hydraulic conductivity of cullet specimens, having maximum size of 3 and 20 mm, compacted with the modified proctor energy, ranges between 10–5 ÷ 10–4 m/s [4]; k is higher (10–4 ÷ 10–3 m/s) if compacted with the standard proctor test [3];

  • Cullet specimens, having maximum size of 20 mm and subjected for 3 h to a constant water flow, under hydraulic heads ranging between 0.05 ÷ 0.10 m, showed their finer fraction (< 0.3 mm) decreasing up to a maximum amount of 2.6% by weight; for cullet, having maximum size of 3 mm, the finer fraction (< 0.075 mm) decreased up to a maximum amount of 4% by weight.

The slight migration of fines under constant water flow, and the suitable values of hydraulic conductivity make it possible to use cullet in the BCL of MSW landfills. However, none of the literature papers deals with this particular and specific reuse. In this note, a general acceptance procedure is proposed. In particular, the mechanical properties of cullet were defined through laboratory tests, specifically developed for simulating the stress conditions acting on site. The particular nature of the actual loads, due to the compaction machine on tyres, moving slowly on landfill cover (quasi-static loading condition), suggested using of specific laboratory tests referred to as cyclic static punching (CSP) tests. Laying of cullet involves a material degradation due to relative particle displacement, which was investigated by many authors. In particular, Indraratna et al. [5], carrying out cyclic triaxial tests on ballast specimens using a large-scale laboratory apparatus, highlighted that the grains degradation can be divided into three zones, related to existing confining pressure. The zones are defined with increasing confining pressure: (1) DUDZ: dilatant unstable degradation zone (low confining pressures); (2) ODZ: optimum degradation zone; (3) CSDZ: compressive stable degradation zone.

The most significant degradation was observed in the DUDZ, where crushing predominantly occurs at the loading onset with the maximum axial strain and dilation rates, mainly due to angular corners breakage with limited grain failures. Sliding and rolling inhibit the formation of permanent interparticle contacts, thus preventing splitting due to excessive stresses.

The effects of different confining pressures during loading on the evolution of GSD of the material composing of BCL and, consequently, on its hydraulic conductivity k, can be assessed with the CSP tests. The selected samples are considered representative of the investigated granular material, after being subjected to the same number of static punchings. In this way, laboratory tests should be able to provide the required results in terms of particle crushing effects on the material permeability.

Design of the Gas Collection Layer

According to Thiel’s [6] procedure, the design of the final cover of non-hazardous MSW landfills requires: (1) the geotechnical stability of the landfill final cover system, subject to a uplift landfill biogas pressure, must guarantee achieving a proper factor of safety; (2) estimation of the maximum landfill biogas volume to be removed from the MSW body; (3) evaluation of the gas transmissivity of a BCL. This paper deals only with the third topic.

Estimating of Gas Transmissivity of a BCL

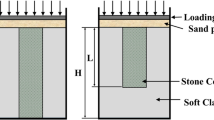
The landfill gas (LFG) transmissivity is defined by putting in relation permeable strip drains (spaced D), landfill gas flux per unit area qLFG, and landfill gas pressure ug (Fig. 1). The relationship is obtained under these assumptions:

  • The LFG flux is assumed to be uniformly distributed into the BCL and symmetric to the centerline among the strip drains; gas volume, being carried in the gas-relief layer, linearly increases from 0, at the center line x = L = D/2, to the maximum value at the strip drain position x = 0. The volume gas per unit width can be written in terms of gas flux as:

    $$ Q_{{{\text{LFG}}}} \left( x \right) \, = \, q_{{{\text{LFG}}}} \left( {L - x} \right) \left[ {{\text{m}}^{3} /{\text{s}}} \right] $$
    (1)

where QLFG(x) is the gas flow rate per unit width at any point x in the gas-relief layer;

Fig. 1
figure 1

Thiel schematic representation of the gas relief layer, section view

Full size image

  • Gas flux in the gas-relief layer can be evaluated by the Darcy’s law, applied to fluid flow in porous media where the flow is laminar, which can be written as follows:

    $$ \begin{aligned} Q_{{{\text{LEG}}}} (X) & = \left( {\frac{{k_{g} }}{{\gamma_{g} }}} \right) \cdot A \cdot \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) = \left( {\frac{{k_{g} }}{{\gamma_{g} }}} \right) \cdot (t \cdot 1) \cdot \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) \\ & = \left( {\frac{{k_{g} \cdot t}}{{\gamma_{g} }}} \right) \cdot \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) = \left( {\frac{{\psi_{g} }}{{\gamma_{g} }}} \right).\left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) \\ \end{aligned} $$
    (2)

    where du/dx is the pressure gradient that drives the LFG from regions of higher pressure to those of lower pressure within the gas-relief layer, kg gas conductivity, γg gas unit weights, A the cross-sectional area and ψg gas transmissivity. Combining Eqs. (1) and (2) and solving the differential equation for x = 0 and x = L/2 where the pressure value is null and maximum, respectively:

    $$ \frac{{\psi_{g} }}{{\gamma_{g} }} \cdot \frac{{{\text{d}}u}}{{{\text{d}}x}} = q_{{{\text{LFG}}}} \cdot (L - x) $$
    (3)

The relationship can be used to determine the required minimum gas transmissivity ψg:

$$ \psi_{g} = \frac{{\gamma_{g} \cdot q_{{{\text{LEG}}}} }}{{u_{{{\text{gmax}}}} }} \cdot \left( {\frac{{L^{2} }}{2}} \right) $$
(4)

where ugmax is the maximum uplift gas pressure value calculated imposing the minimum FS value required for achieving the geotechnical stability of capping.

The Design Hydraulic Conductivity

Through the intrinsic permeability definition, under laminar flow conditions, gas transmissivity may be converted to the water one, or vice versa, easily for granular materials [7] using the following equation:

$$ \frac{{k_{w} }}{{k_{g} }} = \frac{{\mu_{g} }}{{\mu_{w} }} \cdot \frac{{\gamma_{w} }}{{\gamma_{g} }}\quad \psi_{w} = \frac{{\mu_{g} }}{{\mu_{w} }} \cdot \frac{{\gamma_{w} }}{{\gamma_{g} }} \cdot \psi_{g} $$
(5)

where ψw is the water transmissivity of layer, kw the water conductivity, μ the dynamic viscosity in [N s/m] of water (w) and gas (g) and γw the unit weight of water in [N/m3]. Fluid dynamic viscosity and unit weight can be found in the literature for a given temperature, if a typical composition for the LFG is assumed, otherwise they will have to be calculated. Using the values reported in Table 1 and according to Eq. (5), a ratio between hydraulic and gas conductivity of about 10 is obtained. The procedure can be summarized as follows: (1) a suitable factor of safety is defined for overall stability of capping; (2) the maximum allowable uplift gas pressure is consequently obtained; (3) the theoretical gas transmissivity is derived from Eq. (4); (4) the actual design gas transmissivity is derived applying proper correction factors; (5) the design gas conductivity is obtained using the transmissivity definition; (6) the design hydraulic conductivity value is evaluated according to the water–gas conductivity ratio (Eq. 5).

Table 1 Fluid parameters evaluated at 20 °C, under atmospheric pressure (LFG (45%CH4, 55%CO2))
Full size table

Correlation Between Hydraulic Conductivity and GSD of Granular Material

In order to achieve a suitable safety level, the granular material has to assure an appropriate hydraulic conductivity, which is typically determined using constant head laboratory tests or simply estimating it by means of empirical equations. In particular, many researchers [8] have investigated the relationship between hydraulic conductivity and the grain size distribution of granular materials, and the most commonly used is probably the Hazen formula, for loose sands:

$$ k_{w} = c \cdot (D_{10} )^{2} $$
(6)

where kw is in [cm/s], c is assumed equal to 100 and D10 in [cm] is the effective grain size grain corresponding to the 10% of the material being smaller by weight. This formula produces a rough estimate of the hydraulic conductivity of sands, since the known influence of the void ratio and several other factors are not taken into account. It is known that a small quantity of silt and clay in a sandy soil may change the hydraulic conductivity substantially. Moreover, recent experimental studies have shown that the magnitude of c for different granular soils may vary up to 3 orders of magnitude making the Hazen equation highly unreliable [9]. Nevertheless, this relationship is considered useful and suitable to the purpose of the present work. It allows to get quick information about the order of magnitude of the hydraulic conductivity, before and after crushing phenomena, using the Lade and Yamamuro [10] particle crushing parameter (B10), which is based on the D10 particle size:

$$ B_{10} = 1 - \frac{{D_{10(f)} }}{{D_{10(i)} }} $$
(7)

where D10(f) and D10(i) are the effective grain size, respectively, at the end and the beginning of crushing tests. Therefore, considering the Hazen equation and assuming a design hydraulic conductivity of 10–4 m/s to be satisfied, the D10(f) should be ≥ 0.1 mm. This limit could represent a reference value to assess the suitability of the BCL-forming granular material and must be verified by laboratory permeability tests.

Geotechnical Characterization

The BCL must have a transmissivity able to capture and drain all the biogas produced by the solid waste mass. The development of excessive gas pressures inside the BCL could favor the geotechnical instability of capping. For this reason, the minimum k of the granular material, composing the BCL, must be determined through a detailed geotechnical characterization. Laboratory tests, specifically elaborated, have been performed [11]. In particular, appropriate mechanical properties allow to minimize the effects of particle crushing that could occur especially due to applied quasi-static loads during the compaction phase of the overlying mineral liners. The minimization of particle crushing is required to avoid an unacceptable production of fines, which influence the material permeability, as a consequence of a reduced void ratio [12]. This can threaten the fulfilment of grain size compatibility criteria and, therefore, the structure safety.

Innovative Laboratory Test

The test execution method of the cyclic static punching allows to express the mechanical properties of the investigated material, not disregarding its discontinuous nature, in accordance with the configuration of the final multilayered cover system. The test aim is to simulate, within experimental limits and with an adequate safety margin, the stress states that the material undergoes in situ due to particular quasi-static loading conditions triggered by the slow passage of the compaction machine above the mineral liners. The main focus of this study is the spreading phenomena observed in situ and their effects on the final material gradation. Potential void ratio variations, due to particle redistribution processes with a BCL vertical contraction, as a consequence of the pronounced deformability of the underlying waste mass, were not considered in this study. The laboratory test simulates a cyclic quasi-static load through a series of subsequent static punchings applied by an oleo-pneumatic piston press. Once reached, the design pressure is maintained roughly for one second. The applied pressure is equal to 200 kPa and represents a widely conservative value, considering that ground-pressure charts provided by manufacturers of articulated trucks set the pressure at 324 kPa, assuming maximum payload conditions (a gross vehicle weight of ≈ 600 kN) and no tyre penetration. This value is reduced since a thick clay layer is placed above the granular material and a stress diffusion occurs into the layer.

In the laboratory, the cullet specimen is prepared within a standard cylindrical metallic mold (Fig. 2) with an internal diameter of 152 mm without any initial compaction. (Density is established in accordance with that determined on site.) The initial height of the specimen within the metallic mold is 116.5 mm levelling out the material with respect to the upper mold edge. According to the Standards ASTM D698 [13] and D1557 [14], the ratio between the maximum diameter of the tested aggregate and that of the containing cylindrical mold is conservative. The cylindrical mold size also allows to give meaningfulness to constant head permeability tests, upstream and downstream CSP tests, that should be performed to confirm the suitability of the investigated material to fulfil the design goal. Moreover, the thickness of the specimen is adequate to comply with the in situ BCL thickness-tyre print proportions. Indeed, if the material maximum diameter was represented by the 3/4″ sieve (19.0 mm) and the retained at the 3/8″ sieve (9.5 mm) was < 35%, the standards suggest a diameter of the mold of 152 mm.

Fig. 2
figure 2

Standard metallic mold used for CSP test

Full size image

For a comparative purpose, the fixed pressure was applied using two different circular plates (Fig. 3). In this way, the effects on the particle breakage due to the changes of the confining pressure and of boundary conditions have been investigated. The choice of the diameters of the test plates was made by trying to simulate in laboratory the actual action of a tyre on the investigated material. To this end, plates of dimensions already available for other geotechnical laboratory tests were used. The first one, with a diameter D = 150 mm, is able to prevent any upward oriented particle migration during loading (it basically covers the entire specimen top surface) ensuring a complete material confinement, thus minimizing horizontal particle adjustments. A second circular plate with a diameter of 130 mm, smaller than the mold diameter (152.4 mm), is used to transfer the design load to the specimen allowing partial lateral backflow phenomena observed in situ. Indeed, using this smaller plate, the upper particles in the annulus, between the mold wall and the circular plate itself, could move upward during loading, allowing a certain horizontal adjustment of particles due to rotational and translational movements. The GSD of each of these representative specimens is obtained through dry sieving carried out before and after CSP tests, such as to compare the initial GSD curve and the GSD curve obtained after particle breakage phenomena, expected during the loading phase. For the cases based on the 130-mm-wide circular plate, the constant head permeability tests are carried out on two representative specimens and the permeability determined as it is, i.e. before loading and after the compaction. The thickness, and therefore the void ratio, of the specimen undergoing the CSP test changes due not only to particle breakage, but also to a particle adjustment. The void ratio variation effects on the permeability have been cautiously determined taking into account a vertical contraction of the specimen due to particle rolling and sliding and induced breakage phenomena.

Fig. 3
figure 3

Two different circular plates used in the CSP tests

Full size image

The detailed test procedure was the following:

  • Dry sieving of the granular material as it is, at least eliminating the retained at the 19-mm sieve and the potential fine content (< 0.075 mm) (the material, potentially suitable to be employed, is supposed to be initially without fines) and preparation of identical specimens;

  • Dry sieving tests for all the specimens subjected to CSP tests (initial GSD);

  • CSP tests by using a loading circular plate with a diameter D = 130 mm and with a diameter D = 150 mm on specimens reconstructed with the same procedure; the number of static punchings is fixed equal to 10, chosen on the basis of the expected in situ number of dumper passes, and the rate of loading and unloading phases will be representative of in situ observed conditions;

  • Dry sieving tests for the specimens subjected to the first series of CSP tests (final GSD);

  • Constant head permeability test for the granular material as it is prepared inside the cylindrical mold (diameter of 152.4 mm, height of the specimen without compaction 116.5 mm);

  • Constant head permeability test for the granular material after being subjected to compaction, using the 130-mm-wide circular plate; the material undergoes void ratio variations due to breakage and vertical contraction.

Investigated Material

The investigated material was a waste granular material, classified as sifted from glass or cullet. The density of particles ρs was taken equal to 2.45 Mg/m3. The larger particles were characterized by an elongated shape and were often somewhat thin with clear sharp angles, while smaller particles are characterized by a more rounded shape (Fig. 4). No criticality for possible interlocking was highlighted. The samples, taken from the whole bulk material and dried in the oven at 105 °C, were mixed many times in order to ensure a homogeneous distribution of all the sieve fractions (initial GSD). The initial dry unit weight without any compaction was, on average for the specimens, γd = 13.7 kN/m3.

Fig. 4
figure 4

Investigated material, classified as sifted from glass or glass cullet (representative specimen)

Full size image

Results and Discussion

CSP tests carried out using the 130-mm- and 150-mm-wide circular plate are hereafter referred to as Ax and Bx, respectively. The void ratio reduction during CSP tests for all the specimens is plotted in Fig. 5. The largest reduction in the void ratio occurs in the first load cycle. The decrease in void ratio recorded during the tests ranges between 18% ÷ 25% after the first punching and 23% ÷ 32% after ten loading cycles. After CSP tests, the GSD curves of tested representative portions similarly evolve as a consequence of particle breakage phenomena occurring during loading (Fig. 6a–d). In this case, the increase in finer sieve fractions is not of concern in terms of potential reduction in hydraulic conductivity. Indeed, the actual D10 is always greater than 2 mm (Fig. 6a–d) and, therefore, greater than 0.1 mm, the minimum value necessary to ensure the previously stated hydraulic conductivity of 10–4 m/s, according to the Hazen’s equation. However, this preliminary evaluation has to be confirmed by permeability tests before any actual use of the material using a filter criteria design.

Fig. 5
figure 5

Void index variation during CSP tests as a consequence of particle breakage and particle adjustment due to rolling and sliding

Full size image
Fig. 6
figure 6

GSD curve before and after CSP tests for specimens A1 (a), A2 (b), B1 (c), B2 (d)

Full size image

The particle breakage factor B10 [10] is reported in Table 2 together with hydraulic conductivity values estimated by the Hazen’s equation (c = 100). The highest index is achieved by the specimen B2, while the lowest hydraulic conductivity value by the specimen B1, being characterized by the lowest D10(f). For the specimen B2, the comparison between the retained %, before and after CSP tests, was carried out (Figs. 7 and 8). After CSP tests, the retained percentage decreases for larger particles, 9.50 mm and 4.75 mm, while it increases for the remaining sieves. On average, the percent in weight finer than ASTM 200 sieve openings is roughly 0.05% after CSP tests. The final percent passing values, which result from the amount of particle breakage, appear not to be affected by different load application conditions, as expected according to literature results. The main reason may be found in the particular shape of the larger particles of the investigated material that, being elongated and thin, are disincline to move due to rotation or translation preferring to crush due to fracture instead. The most significant degradation seems to occur at the onset of loading, when the axial strain rate is at its maximum and particle breakage occurs due to fracture and angular corner breakage, as a consequence of the particle sharp angles. This is also confirmed by the comparison of the retained percentage, before and after CSP tests, where the increase in middle diameter particles clearly indicates corner breakage or medium-size particle fractures (Figs. 7 and 8). Abrasion and friction grain breakage explains the observed but limited increase in the amount of finer fractions. Hydraulic conductivity of two specimens, A3 and A4, was determined. While the specimen A3 was subjected to the permeability test as it was, with a γd = 13.7 kN/m3 (corresponding to a void ratio e = 0.785) and a thickness of 116.5 mm, the specimen A4 with a similar initial void ratio was subjected to a CSP test using the 130-mm-wide circular plate, before undergoing the permeability test. After CSP test, the thickness of the specimen A4 had an average value of 105 mm with, therefore, a reduction of 11.5 mm. The corresponding void ratio was e = 0.599. The obtained hydraulic conductivity values for the two specimens are reported in Table 3 together with the water temperature and the correction factor for viscosity RT, namely RT =  − 0.02452 T + 1.495, to be used in Darcy’s equation. A slight reduction in the hydraulic conductivity value after the CSP test can be observed. This reduction is an evident consequence of a reduced void ratio, resulting from both particle crushing phenomena and a vertical specimen contraction due to particle adjustments by rotational and translational movements. The values, obtained with a widely conservative laboratory procedure, demonstrate the suitability of the investigated material to be used in the BCL implementation, provided that filter design criteria are fully satisfied.

Table 2 Lade and Yamamuro particle breakage factor, final effective grain size and Hazen’s hydraulic conductivity
Full size table
Fig. 7
figure 7

Comparison between partial retained % before and after CSP tests—B2 test

Full size image
Fig. 8
figure 8

Blow-up of the comparison between partial retained % at smaller sieve sizes, before and after CSP tests—B2 test

Full size image
Table 3 Hydraulic conductivity for specimen P1 and P2
Full size table

Filter Design Criteria

The grain size compatibility of cullet with the foundation layer (i.e. regularization layer placed above wastes, consisting of coarse granular materials) should be achieved. According to the Terzaghi’s empirical retention and permeability criteria, D15b e D85b have to satisfy the following equation:

$$ \frac{{D_{15f} }}{{D_{85b} }} \le 4 \le \frac{{D_{15f} }}{{D_{15b} }} $$
(8)

where D15 and D85 are, respectively, the sizes at which 15 and 85 percent of the total soil particles, composing of the foundation layer (f) or of BCL (b), are smaller. The percentage is by weight as determined by sieve analysis.

Once verified, the absence of cementing minerals and a texture capable of causing interlocking, the possible migration of the fine particles of the layer itself can be controlled using the Kezdi [15] and Kenney and Lau’s [16] methods. In Figs. 9 and 10, the results of these verification methods can be found.

Fig. 9
figure 9

Kezdi’s verification method—B2 test

Full size image
Fig. 10
figure 10

Kenney and Lau’s verification method—B2 test

Full size image

The method proposed by Kezdi [15] divides the granulometric curve of the material, for a specific diameter d, into two parts: (1) the fraction passing through a sieve with opening d (defined as D85b) and (2) the corresponding retained fraction (defined as D15f). The filter retention criterion of Terzaghi (D15f/D85b ≤ 4) must be satisfied for a set of different diameters characterizing the granulometric curve of the investigate material, establishing its “internal stability". Kezdi's criterion, however, is excessively conservative, as the finest particles (particles < 0.85 mm for cullet) normally tend not to satisfy the retention criterion; this does not mean that the material is not self-protected.

For investigating any migration of the finer particles, the method of Kenney and Lau [16] can be used. This method divides a granular soil in two parts: (1) a primary structure remaining stationary in its original position; (2) a secondary structure consisting of the finer particles arranged inside the voids of the primary structure. Particles of the secondary structure tend to move within the voids due to the effects of seepage or vibrations. The primary structure can be treated as a filter, while the particles of the secondary structure can be considered as the base material to be protected. When a mobile particle meets a void of the primary structure, small enough to stop it, it becomes part of the filter. A soil is internally unstable if it is characterized by larger particles unable to block smaller ones, with consequent erosion of the layer and washout of fine particles. From the observation of a large number of experimental tests, Kenney and Lau [16] clearly noted the relationship between internal instability problems and the shape of the particle size distribution curve. The method consists in comparing the passing F(%), at a specific diameter D, with H (%), fraction evaluated between the diameters D and 4D. Plotting the H–F curve, it is possible to evaluate the position of this curve with respect to the limit line (H = F) that indicates the minimum value of H required for the material to be internally stable.

Figures 9 and 10 show that the investigated cullet can be classified as suitable to the design purpose, since the granular material, composing the cover foundation layer, respects the previous requirements.

Conclusions

The multilayer barriers of the MSW landfills include a layer of granular soil below the mineral liner for biogas drainage. This draining layer must maintain its geometric thickness, hydraulic conductivity and particle size distribution over time. A very attractive and economical alternative to gravelly soil is a recyclable solid waste, consisting of glass fragments of various sizes and colours (cullet). This option has the undeniable positive effect of reducing the carbon footprint of MSW landfills by avoiding the excavation of coarse granular material from a quarry. The focus of this paper is the definition of a test procedure to verify the capability of using cullet as a biogas drainage. Cullet is required to have an adequate crushing strength when stressed with static or cyclic loads. The possibility of crushing and the consequent potential change in its grain size distribution need to be avoided, as a partial formation of fine material can result in a decrease in the initial thickness and the overall permeability of the drainage layer. Since cullet is an atypical material, the usual geotechnical laboratory tests cannot be directly applied to it. Its resistance to crushing under static and cyclic loading was assessed through an innovative CSP test, proposed by the authors. The test simulates, within certain experimental limits and with an adequate safety margin, the stress state to which the biogas drainage layer is subjected in the operating conditions. In particular, the slow passage of the compacting trucks constitutes a significant load condition for the landfill coverage system. The main results of the study can be summarized as follows. The granulometric curves of various cullet samples, reconstructed with the same procedure and thereafter tested with CSP, similarly evolve as a consequence of particle breakage phenomena occurring during loading. The increase in the finer fraction does not cause a significant reduction in the hydraulic conductivity. Furthermore, the percentage of the new finer fraction seems not to be affected by different loading conditions. This could be due to the elongated and thin shape of the larger particles of the cullet that are disincline to rotate or translate preferring to crush. Many angular corner breakages develop as a consequence of the particle sharp angles. Comparing the granulometric curves obtained before and after CSP tests, an increase in middle diameter grains can be noticed; this clearly indicates corner breakage or medium-size particle fractures. Tested cullet showed a very limited increase in the amount of finer fractions. A low reduction in the hydraulic conductivity due to the void ratio decrease was observed after the CSP tests. The range of hydraulic conductivity shows the suitability of cullet to be used in the BCL, provided that filter design criteria are fully satisfied. The cullet grain size compatibility with the underlying foundation layer should be imposed as well as its capability of self-healing. This has been verified using the Kezdi [15] and Kenney-Lau [16] methods. In conclusion, cullet can be classified as suitable to the BCL purpose, provided that it respects the required properties previously mentioned.