Introduction

In the last decade, the natural polymer and biopolymer adsorbents have received great attention for the removal of environment contaminants [1]. Among the various types of polymers, chitosan (β-(1-4) acetyl-d-glucosamine), as the second most abundant linear biopolymers in nature, and its derivatives have attracted significant interest in water treatment [2–5]. It is harmless to humans and has been widely used in food, medical and pharmaceutical processes [6, 7] and can be commercially produced by the chemical deacetylation of chitin as a major component of the exoskeleton of crustaceans [8].

Chitosan was found as an effective low-cost adsorbent with high adsorption potential for various organic and inorganic pollutants, due to its high amino and hydroxyl functional groups content [6, 9]. In recent years, many researchers have worked to improve the chitosan adsorption performance by synthesis/modification of its derivatives [5, 6, 10]. In this regard, the magnetic chitosan composites have received attention due to the fact that they are low-cost materials and enable simple separation after the adsorption process [11–13]. For instance, several magnetic chitosan composites such as chitosan/Fe3O4 [14–16], chitosan/Al2O3/Fe3O4 [17, 18], polyoxometalate-grafted chitosan/Fe3O4 [19] and magnetic graphene/chitosan [8] have been reported as efficient adsorbent composites for the removal of organic pollutants. Also, Zhao et al. [15, 20], Ayati et al. [21], Ren et al. [22] and Yang et al. [23] used the magnetic chitosan composites for the adsorption of different metal ions adsorption as well as Reddy et al. [24] and Vakili et al. [10] who studied the adsorption performance of magnetic chitosan composites for metal and dyes removal from aqueous solutions. The works in the literature have been mostly focused on the synthesis and adsorption mechanism and highlighted the effective parameters on the adsorption capacity of these composites.

ANFIS, as an adaptive multilayer feed-forward network, is a fuzzy interference system combined with the computational power of artificial neural network (ANN) [25]. ANFIS is a powerful approach to modeling/mapping the input and output relationship in complex and nonlinear systems [26, 27]. It converges much faster and has the most efficient learning algorithm, comparing with other models [28]. In recent years, the neural fuzzy inference system (ANFIS) as an artificial intelligence technique has successfully been utilized for modeling and simulation of various kinds of adsorption processes in water treatment and purification [29–33]. Ghaedi et al. [32] reported the use of adaptive neuro-fuzzy inference system model for adsorption of 1,3,4-thiadiazole-2,5-dithiol onto gold nanoparticles-activated carbon. They have also studied the application of principal component analysis–adaptive neuro-fuzzy inference system (PCA–ANFIS) in the methylene blue adsorption by activated carbon [33]. In another study, Mandal et al. [34] used the ANFIS for modeling the adsorptive removal of As(III) and Cr(VI) ions in batch and column mode using the fibrous zirconium oxide ethylenediamine adipate (ZEDA). Also, Rebouh et al. [35] applied the ANFIS technique for the prediction of metal ions removal capacity from aqueous solution by wheat straw biosorbent. Moreover, Qasaimeh et al. exploited the ANFIS to assess the conditions required for aquatic systems to serve as a sink for metal ions removal [36]. The adsorption modeling basically has two advantages: (1) development a relation between input and output effective parameters irrespective of behavior and (2) finding the optimal condition for the removal of target pollutant which has been verified by confirmatory experimental run.

To the best of our knowledge, despite the extensive research on the adsorption performance of magnetic chitosan composite, their modeling by ANFIS as a very effective approach has been overlooked in batch adsorption process. In the present work, the proposed useful and cost-effective ANFIS technique is applied for quantitative sorption of methyl orange (MO) using a recently introduced magnetic chitosan [17], composed of chitosan-coated magnetic Al2O3/Fe3O4 core–shell, as an effective and acid-resistant adsorbent for the treatment of wastewater.

Experimental

Chemicals and instruments

The used chitosan, acetic acid (100%) and absolute methanol were purchased from Acros Organics, VWR and Altia companies, respectively, and all other chemicals were obtained from Sigma-Aldrich Co. The prepared composite was characterized by Hitachi S-4800 ultra-high resolution scanning electron microscope.

Adsorbent synthesis

The magnetic chitosan/Al2O3/Fe3O4 (CAF) composite was prepared according to our recent work [18], in which the Fe3O4 microspheres were prepared using hydrothermal method. 100 mg of the prepared microspheres was dispersed in the aluminium isopropoxide solution in ethanol (16.6 g L−1), followed by dropwise addition of water and ethanol mixture (1:5 (v/v)). The obtained particles were washed with ethanol, dried at 500 °C for 3 h and dispersed in acetic acid (2 wt%). Then, glutaraldehyde solution (25%) was added to the mixture to form a gel. The formed gel was dried in oven at 60 °C for 12 h, washed several times with acetic acid solution and water and dried at 50 °C for 12 h. The morphology of the prepared CAF is shown in Fig. 1.

Fig. 1
figure 1

SEM image of prepared magnetic chitosan

Full size image

Adsorption experiments

The MO adsorption onto CAF composite has been performed in the batch mode. In this regard, specific amount of CAF (according to the experiment design) was added to a 10-mL MO solution with desired concentration and pH. HCl and NaOH solutions (0.01 M) were used for pH adjustment. The solutions were shaked on the Lab Teamet ST5 CAT shaker at 100 rpm. Finally, they were filtered by a 0.45-µm syringe filter and analyzed with UV spectrophotometer (JASCO V-670 spectrophotometer, Japan). The MO concentrations (C) were obtained through the absorbance value at λ max = 464 nm.

ANFIS theory

By combination of the fuzzy systems and ANN, the ANFIS is a powerful tool which benefits from both the learning characteristics of the neural networks and the inference fuzzy model [26]. The ANFIS is composed of antecedent and conclusion parts that are connected to each other by the fuzzy rules in network form. Generally, two fuzzy if–then rules are used in this system as follows:

Rule 1: If x 1 is A 1 and x 2 is B1 and…; then f 1 = p 1 x 1 + q 1 x 2 + ··· + r 1

Rule 2: If x 1 is A 2 and x 2 is B 2 and…; then f 2 = p 2 x 1 + q 2 x 2 + ··· + r 2

where f i is output and p i , q i , k i and r i are the consequent parameters of ith rule. A i and B i represent the linguistic labels whose membership function parameters are premise parameters and are represented by fuzzy sets [27].

ANFIS consists of five layers, namely, a fuzzy layer, a product layer, a normalized layer, a defuzzy layer and a total output layer [27, 37]. In the first and fourth layers, the nodes are adaptive and some used parameters in these nodes are determined through training phase, whereas the nodes in other layers are fixed. The node function for the input variable, x, in the first layer is as follows

$$\mu_{Ai} (x) = e^{{ - ((x - x^{*} )/\sigma^{2} )}},$$
(1)

where x* and σ are the mean and variance of function, respectively, which are called premise parameters and can be updated during the process. In the second layer, as product layer, the output of each node is an algebraic product of the input signals. The firing strength of each rule, ω i , can be calculated using the following equation:

$$\omega_{i} = \mu_{Ai} (x_{1} ) \times \cdots \times \mu_{Ci} (x_{n} )$$
(2)

The normalization layer is the third layer in which the output of each node is computed by the ratio of the ith rule’s firing strength to the sum of all rules’ firing strengths as follows

$$\overline{{\omega_{i} }} = \omega_{i} /(\omega_{i} + \cdots + \omega_{n} )$$
(3)

Fourth layer is the defuzzification layer and the output of each node is obtained by the following equation:

$$O_{4,i} = \sum {\overline{{\omega_{i} }} } f_{i}$$
(4)

Finally, the last layer calculates the total sum of the all input signals overall as final output [27]:

$${\text{output}} = \frac{{\sum\nolimits_{i = 1}^{n} {\omega_{i} f_{i} } }}{{\sum\nolimits_{i = 1}^{n} {\omega_{i} } }}$$
(5)

The training procedure is shown in Fig. 2.

Fig. 2
figure 2

Block diagram representation of training algorithm for ANFIS [27]

Full size image

Model specification

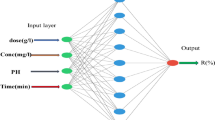
Based on the earlier studies [17, 18], the pH, adsorbent dosage, initial concentration and contact time were found as main four effective parameters in the MO adsorption process onto the CAF. In this regard, these parameters were selected for the training and testing of the models, and the appropriate ranges for these factors were defined accordingly. The percentages of MO removal, R%, and MO uptake at t time (mg/g), q t , were chosen as outputs and calculated as follows:

$$R(\% ) = \frac{{C_{\text{o}} - C_{\text{t}} }}{{C_{\text{o}} }} \times 100,$$
(6)
$$q_{t} = \frac{{(C_{\text{o}} - C_{\text{t}} )}}{m}V,$$
(7)

where C o and C t (mg/L) are the MO concentrations at initial and t time, respectively; V (L) is the solution volume, and m (g) is the adsorbents dosage.

As listed in Table 1, the experiments were randomized in two deigned blocks by experiment software (Design-Expert 8 trial version).

Table 1 Experimental design for MO adsorptive performance onto CAF
Full size table

Results and discussion

In the present work, extensive experimental data of adsorptive performance of magnetic chitosan were applied to the developed ANFIS model to predict and calculate the output variables. It can minimize the experiment numbers for obtaining the highest adsorption efficiency using the existing historical experimental data as well as predicting the unknown data. In this regard, the available data set was divided into two sets; about 75% of them was used for training and the other (about 25%) for testing the performance. Training and testing samples must be different and randomly selected from original data set. In this work, there were 30 experimental results, each one of which was used for both training and validation. Therefore, 22 data were used for training and 9 data were used for validation and for determining the precision of the obtained ANFIS model.

The ANFIS information used in this study with the back propagation optimum method is shown in Table 2. To train the network, 22 sets of data selected randomly were used as inputs. The training was accomplished with a 0.02 learning rate, and 180 iterations were needed.

Table 2 The used ANFIS information
Full size table

The fuzzy model rule surfaces showing the relationship between the adsorbent dosage, initial pH, MO initial concentration and contact time with the adsorption removal efficiency are given in Fig. 3. Also, the fuzzy rule surfaces for the effect of the mentioned input parameters on the MO uptake amount by the adsorbent are shown in Fig. 4. These figures obviously illustrate the relationship between input and output data and the influence of each parameter to obtain the optimum output values.

Fig. 3
figure 3

Generalization of best-fitted surfaces predicted with ANFIS models for removal

Full size image
Fig. 4
figure 4

Generalization of best-fitted surfaces predicted with ANFIS models for q t

Full size image

The ANFIS model showed good correlation coefficient values (R 2 = 0.99), as well as excellent fitness of predicted and experimental values. Comparing the experimental and obtained results indicated an acceptable agreement between ANFIS model outputs and obtained experimental data which have a good accuracy (Fig. 5), so that the error in the training and test data is very low.

Fig. 5
figure 5

Comparison of experimental data and predicted data by ANFIS for a removal, b q t

Full size image

The prediction of ANFIS model has been compared with the experimental data. Figures 6 and 7 represent the ANFIS prediction values versus actual data of MO removal efficiency and MO uptake amount onto the magnetic chitosan adsorbent. As can be seen, the obtained correlation coefficient values were more than 0.99, demonstrating that the ANFIS model predicted the measured data satisfactorily, and that the neuro-fuzzy model training was successfully accomplished. Also, the prediction performance of model was quantified using the following statistical standards: mean square error (MSE), mean absolute error (MAE), root mean square error (RMSE) and mean absolute percentage error (MAPE) which are defined as follows, respectively [27]:

Fig. 6
figure 6

Comparison of model predictions removal of adsorptive performance with experimental data at different conditions

Full size image
Fig. 7
figure 7

Comparison of model predictions q t with experimental data at different conditions

Full size image
$${\text{MSE }} = \, \frac{{\sum\nolimits_{i = 1}^{n} {(\mathop {y^{\prime}}\nolimits_{i} - \mathop y\nolimits_{i} )^{2} } }}{n}$$
(8)
$${\text{MAE }} = \, \frac{{\sum\nolimits_{i = 1}^{n} {\left| {\mathop {y^{\prime}}\nolimits_{i} - \mathop y\nolimits_{i} } \right|} }}{n}$$
(9)
$${\text{RMSE }} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {(\mathop {y^{\prime}}\nolimits_{i} - \mathop y\nolimits_{i} )^{2} } }}{n}}$$
(10)
$${\text{MAPE }} = \, \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{\mathop {y^{\prime}}\nolimits_{i} - \mathop y\nolimits_{i} }}{{\mathop y\nolimits_{i} }}} \right|}$$
(11)

where y i and \(y_{i}^{'}\) are the ith actual value and predicted value for the training and test data respectively. These parameters for ANFIS model of the MO adsorption onto the CAF surface are listed in Table 3.

Table 3 The obtained statistical parameters for MO adsorption onto CAF which is modeled by ANFIS
Full size table

Furthermore, the predicted MO removal efficiency and MO uptake by CAF using ANFIS for training and test data were compared with experimental data in Figs. 6 and 7, respectively. The results obviously indicated that the ANFIS system can effectively model the non-linear behavior of the adsorptive performance under different operating conditions. To obtain these objectives, the MATLAB 2014 software was employed in this work.

Conclusion

In this paper, the adaptive neural fuzzy inference system (ANFIS) was designed for the modeling of MO adsorptive removal by as-prepared magnetic chitosan. The performance of ANFIS prediction was compared with experimental results using the MAE, MSE, RMSE, MAPE and the correlation coefficient (R 2) values. The developed ANFIS models showed an excellent regression analysis with an R 2 > 0.99 as well as a good fitness of predicted and experimental values for the studied process.