Skip to main content
SpringerLink
Log in

Numerical study of nonlinear generalized Burgers–Huxley equation by multiquadric quasi-interpolation and pseudospectral method

  • Original Research
  • Published:
Mathematical Sciences Aims and scope Submit manuscript

Abstract

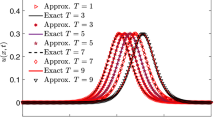
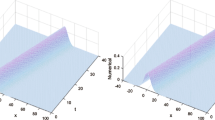
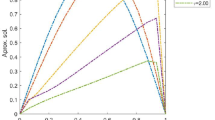
This paper develops an efficient numerical meshless method to solve the nonlinear generalized Burgers–Huxley equation (NGB-HE). The proposed method approximates the unknown solution in the two stages. First, the \(\theta\)-weighted finite difference technique is adopted to discretize the temporal dimension. Second, a combination of the multiquadric quasi-interpolation and pseudospectral (denoted by MQQI-PS) is constructed to approximate the spatial derivatives. In addition, a cross-validation technique is used to find the shape parameter value. Finally, numerical results are illustrated to show the accuracy and efficiency of the MQQI-PS method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Wang, X.Y., Zhu, Z.S., Lu, Y.K.: Solitary wave solutions of the generalised Burgers-Huxley equation. J. Phys. A 23(3), 271–274 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  2. FitzHugh, R.: Mathematical models of excitation and propagation in nerve. In: Biological Engineering. Schwan, H.P.(eds), New York: McGraw Hill (1969)

  3. Bratsos, A.G.: A fourth-order numerical scheme for solving the modified Burgers equation. Comput. Math. Appl. 60(5), 1393–1400 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Çelik, I.: Haar Wavelet method for solving generalized Burgers-Huxley equation. Arab J. Math. Sci. 18(1), 25–37 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Javidi, M., Golbabai, A.: A new domain decomposition algorithm for generalized Burger’s-Huxley equation based on Chebyshev polynomials and preconditioning. Chaos Solitons Fractals 39(2), 849–857 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dehghan, M., Saray, B.N., Lakestani, M.: Three methods based on the interpolation scaling functions and the mixed collocation finite difference schemes for the numerical solution of the nonlinear generalized Burgers-Huxley equation. Math. Comput. Model. 55(3–4), 1129–1142 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Mohammadi, R.: B-spline collocation algorithm for numerical solution of the generalized Burger’s-Huxley equation. Numer. Methods Partial Differ. Equ. 29(4), 1173–1191 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Mohan, M.T., Khan, A.: On the generalized Burgers-Huxley equation: Existence, uniqueness, regularity, global attractors and numerical studies. Discrete Contin. Dyn. Syst. Ser. B 26(7), 3943–3988 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Zhong, M., Yang, Q.J., Tian, S.F.: The modified high-order Haar wavelet scheme with Runge-Kutta method in the generalized Burgers-Fisher equation and the generalized Burgers-Huxley equation. Mod. Phy. Lett. B. 35(24), 2150419 (2021)

    Article  MathSciNet  Google Scholar 

  10. Çiçek, Y., Korkut, S.: Numerical solution of generalized Burgers-Huxley equation by Lie-Trotter splitting method. Numer. Anal. Appl. 14(1), 90–102 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  11. Wang, K.J.: Variational principle and approximate solution for the generalized Burgers-Huxley equation with fractal derivative. Fractals. 29(2), 2150044 (2021)

    Article  MATH  Google Scholar 

  12. Shukla, S., Kumar, M.: Error analysis and numerical solution of Burgers-Huxley equation using 3-scale Haar wavelets. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-01037-4

  13. Alinia, N., Zarebnia, M.: A numerical algorithm based on a new kind of tension B-spline function for solving Burgers-Huxley equation. Numer. Algorithms 82(4), 1121–1142 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Abbasbandy, S., Ghehsareh, H.R., Hashim, I.: Numerical analysis of a mathematical model for capillary formation in tumor angiogenesis using a meshfree method based on the radial basis function. Eng. Anal. Bound. Elem. 36(12), 1811–1818 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Abbasbandy, S., Azarnavid, B., Hashim, I., Alsaedi, A.: Approximation of backward heat conduction problem using Gaussian radial basis functions. U.P.B. Sci. Bull., Series A. 76(4), 67–76 (2014)

  16. Chen, W., Fu, Z.J., Chen, C.S.: Recent advances in radial basis function collocation methods. Springer, Berlin (2014)

    Book  MATH  Google Scholar 

  17. Kansa, E.J., Aldredge, R.C., Ling, L.: Numerical simulation of two-dimensional combustion using mesh-free methods. Eng. Anal. Bound. Elem. 33(7), 940–950 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  18. Assari, P., Dehghan, M.: A meshless local discrete Galerkin (MLDG) scheme for numerically solving two-dimensional nonlinear Volterra integral equations. Appl. Math. Comput. 350, 249–265 (2019)

    MathSciNet  MATH  Google Scholar 

  19. Assari, P.: Thin plate spline Galerkin scheme for numerically solving nonlinear weakly singular Fredholm integral equations. Appl. Anal. 98(11), 2064–2084 (2019). https://doi.org/10.1080/00036811.2018.1448073

    Article  MathSciNet  MATH  Google Scholar 

  20. Assari, P., Dehghan, M.: Solving a class of nonlinear boundary integral equations based on the meshless local discrete Galerkin (MLDG) method. Appl. Numer. Math. 123, 137–158 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  21. Assari, P.: The numerical solution of Fredholm-Hammerstein integral equations by combining the collocation method and radial basis functions. Filomat 33(3), 667–682 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  22. Xiao, M.L., Wang, R.H., Zhu, C.G.: Applying multiquadric quasi-interpolation to solve KdV equation. J. Math. Res. Expo. 31(2), 191–201 (2011)

    MathSciNet  MATH  Google Scholar 

  23. Nikan, O., Avazzadeh, Z., Machado, J.T.: Numerical approximation of the nonlinear time-fractional telegraph equation arising in neutron transport. Commun. Nonlinear Sci. Numer. Simul. 99, 105755 (2021)

  24. Powell, M.J.D.: Univariate multiquadric approximation: Reproduction of linear polynomials. In: Multivariate Approximation and Interpolation. Haussman, W. and Jetter, K.(eds), Birkhäuser Verlag, Basel (1990)

  25. Beatson, R.K., Powell, M.J.D.: Univariate multiquadric approximation: Quasi-interpolation to scattered data. Constr. Approx. 8, 275–288 (1992). https://doi.org/10.1007/BF01279020

    Article  MathSciNet  MATH  Google Scholar 

  26. Wu, Z., Schaback, R.: Shape preserving properties and convergence of univariate multiquadric quasi-interpolation. ACTA Math. Appl. Sinica. 10(4), 441–446 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  27. Jiang, Z.W., Wang, R.H., Zhu, C.G., Xu, M.: High accuracy multiquadric quasi-interpolation. Appl. Math. Model. 35(5), 2185–2195 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Singh, B.K., Arora, G., Singh, M.K.: A numerical scheme for the generalized Burgers-Huxley equation. J. Egyptian Math. Soc. 24(4), 629–637 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. El-Kady, M., El-Sayed, S.M., Fathy, H.E.: Development of Galerkin method for solving the generalized Burger’s–Huxley equation. Math. Probl. Eng. 2013 (2013). 10.1155/2013/165492

  30. Hardy, R.L.: Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 176, 1905–1915 (1971). https://doi.org/10.1029/JB076i008p01905

    Article  Google Scholar 

  31. Madych, W.R., Nelson, S.A.: Multivariate interpolation and conditionally positive definite functions. II. Math. Comp. 54, 211–230 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sarboland, M., Aminataei, A.: On the numerical solution of one-dimensional nonlinear nonhomogeneous Burgers’ equation. J. Appl. Math. 2014 (2014). 10.1155/2014/598432

  33. Rashidinia, J., Ghasemi, M., Jalilian, R.: Numerical solution of the nonlinear Klein-Gordon equation. J. Comput. Appl. Math. 233(8), 1866–1878 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Fasshauer, G.E.: RBF collocation methods as Pseudospectral methods. In: Kassab, A., Brebbia, C.A., Divo, E., Poljak, D. (eds.) Boundary elements XXVII, pp. 47–56. WIT Press, Southampton (2005)

    Google Scholar 

  35. Wendland, H.: Scattered data approximation. Cambridge University Press, Cambridge, UK (2005)

    MATH  Google Scholar 

  36. Schaback, R.: Convergence of unsymmetric kernel-based meshless collocation methods. SIAM J. Numer. Anal. 45(1), 333–351 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Emamjomeh, M., Abbasbandy, S., Rostamy, D.: Quasi interpolation of radial basis functions-pseudospectral method for solving nonlinear Klein–Gordon and sine-Gordon equations. Iranian J. Numer. Anal. Optim. 10(1), 81–106 (2020). 10.22067/IJNAO.V10I1.75129

  38. Twizell, E.H.: Computational methods for partial differential equations. Ellis Horwood Limited, Chichester (1984)

    MATH  Google Scholar 

  39. Islam, S., Haq, S., Uddin, M.: A meshfree interpolation method for the numerical solution of the coupled nonlinear partial differential equations. Eng. Anal. Boundary Elem. 33(3), 399–409 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  40. Lee, M.B., Yoon, J.: Sampling inequalities for infinitely smooth radial basis functions and its application to error estimates. Appl. Math. Lett

  41. Fasshauer, G.E., Zhang, J.G.: On choosing optimal shape parameters for RBF approximation. Numer. Alg. 45, 345–368 (2007). https://doi.org/10.1007/s11075-007-9072-8

    Article  MathSciNet  MATH  Google Scholar 

  42. Rippa, S.: An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 11, 193–210 (1999). https://doi.org/10.1023/A:1018975909870

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Central Tehran Branch, Islamic Azad University, Tehran, Iran

    Mahbubeh Rahimi, Hojatollah Adibi & Majid Amirfakhrian

  2. Department of Computer Science, University of Calgary, Calgary, Canada

    Majid Amirfakhrian

Authors
  1. Mahbubeh Rahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hojatollah Adibi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Majid Amirfakhrian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hojatollah Adibi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahimi, M., Adibi, H. & Amirfakhrian, M. Numerical study of nonlinear generalized Burgers–Huxley equation by multiquadric quasi-interpolation and pseudospectral method. Math Sci 17, 431–444 (2023). https://doi.org/10.1007/s40096-022-00461-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40096-022-00461-5

Keywords

Search

Navigation