Introduction

The interest on count data modeling has been greatly increased in the last decade. The widely used distribution for modeling the count data sets is Poisson distribution. The well-known property of Poisson distribution is that its mean and variance are equal. Therefore, Poisson distribution does not work in the case of over-dispersion or under-dispersion. Poisson distribution is widely used in many research fields such as actuarial, environmental, actuarial and economics sciences in spite of its weakness. The reason for that comes from its simple form and easy implementation and software support. To remove the drawback of Poisson distribution, researchers have shown great interest to introduce mixed-Poisson distributions for modeling the over-dispersed or under-dispersed count data sets such as Bhati et al. [1], Imoto et al. [7], Mahmoudi and Zakerzadeh [9], Gencturk and Yigiter [5], Wongrin and Bodhisuwan [15], Déniz [3], Cheng et al. [2], Lord and Geedipally [8], Zamani et al. [16], Sáez-Castillo and Conde-Sánchez [12], Rodríguez-Avi et al. [10], Shmueli et al. [11], Shoukri et al. [13].

As mentioned above, Poisson distribution is insufficient to model the over-dispersed count data sets. The main motivation of this study is to introduce an alternative regression model for modeling the over-dispersed count data sets. Therefore, a re-parametrization of Poisson quasi-Lindley distribution, proposed by Grine and Zeghdoudi [6], is introduced and its statistical properties are studied comprehensively such as mean, variance and estimation problem of the model parameters. The maximum likelihood (ML) and method of moments (MM) estimation methods are considered to estimate the unknown parameters of the re-parametrized PQL distribution. The efficiencies of the estimation methods are compared with extensive simulation study. Using the re-parametrized Poisson quasi-Lindley distribution, a new regression model for over-dispersed count data sets is introduced. To demonstrate the effectiveness of proposed regression model, a real data set on days of absence of the high school students are analyzed with Poisson, negative-binomial and PQL regression models.

The rest of the paper is organized as follows: In “Re-parametrization of Poisson quasi-Lindley distribution” section, the statistical properties of the re-parametrized Poisson quasi-Lindley distribution are obtained. In “Estimation” section, ML and (MM) estimation methods are considered to estimate the unknown model parameters. In “Simulation” section, finite sample performance of estimation methods is compared via a Monte Carlo simulation study. In “Poisson quasi-Lindley regression model” section, a new regression model is introduced. In “Empirical study” section, a real data set is analyzed to demonstrate the usefulness of proposed model against the Poisson and negative-binomial regression models. “Conclusion” section contains the concluding remarks.

Re-parametrization of Poisson quasi-Lindley distribution

Let the random variable X follows a Poisson distribution. The probability mass function (pmf) is

$$\begin{aligned} P\left( x;\lambda \right) = \frac{{\exp \left( { - \lambda } \right) {\lambda ^x}}}{{x!}},\quad x = 0,1,2,\ldots , \end{aligned}$$

where \(\lambda >0\). The mean and variance of Poisson distribution are \(E\left( X\right) =\lambda\) and \({\mathrm{Var}}\left( X\right) =\lambda\), respectively. So, the dispersion index, shortly DI, for Poisson distribution is \(DI = {{\mathrm{Var}\left( X \right) } / {E\left( X \right) = {\lambda / \lambda }}} = 1\). As seen from the dispersion index of Poisson distribution, the over-dispersed or under-dispersed data sets cannot be modeled by Poisson distribution. Note that when the variance is greater than mean, the over-dispersion occurs; otherwise, it is called as under-dispersion. Grine and Zeghdoudi [6] introduced a new mixed-Poisson distribution, called Poisson quasi-Lindley (PQL), by compounding Poisson distribution with quasi-Lindley distribution, introduced by Shanker and Mishra [14]. The pmf of PQL distribution is given by

$$\begin{aligned} P\left( {Y = y} \right) = \frac{\theta }{{\alpha + 1}}\left[ {\frac{{\alpha \left( {\theta + 1} \right) + \theta \left( {y + 1} \right) }}{{{{\left( {\theta + 1} \right) }^{y + 2}}}}} \right] ,\quad y = 0,1,2,\ldots , \end{aligned}$$
(1)

where \(\theta >0\) and \(\alpha >-1\). Hereafter, the random variable Y will be denoted as \({\text {PQL}}\left( \theta ,\alpha \right)\). The corresponding cumulative distribution function (cdf) to 1 is

$$\begin{aligned} F\left( y \right) = P\left( {Y \le y} \right) = 1 - \frac{{\alpha + 2\theta + \alpha \theta + \theta y + 1}}{{\left( {1 + \alpha } \right) {{\left( {1 + \theta } \right) }^{y + 2}}}}. \end{aligned}$$
(2)

The mean and variance of PQL distribution are given by, respectively,

$$\begin{aligned}&E\left( Y \right) = \frac{{2 + \alpha }}{{\left( {1 + \alpha } \right) \theta }} \end{aligned}$$
(3)
$$\begin{aligned}&{\text {Var}}\left( Y \right) = \frac{{2 + 4\alpha + {\alpha ^2} + \theta \left( {\alpha + 2} \right) \left( {\alpha + 1} \right) }}{{{{\left( {\alpha + 1} \right) }^2}{\theta ^2}}} \end{aligned}$$
(4)

Here, the re-parametrization of PQL distribution is considered. The motivation of re-parametrization for PQL distribution comes from the generalized linear model approach.

Proposition 1

Let\(\theta = {{\left( {2 + \alpha } \right) }/} {\left[ {\left( {1 + \alpha } \right) \mu } \right] }\), then the pdf of PQL distribution is

$$\begin{aligned}&P\left( {Y = y} \right) = \frac{{2 + \alpha }}{{{{\left( {\alpha + 1} \right) }^2}\mu }}\nonumber \\&\quad \left\{ {\frac{{\alpha + \left( {2 + \alpha } \right) {{\left( {\mu + \alpha \mu } \right) }^{ - 1}}\left( {y + \alpha + 1} \right) }}{{{{\left[ {1 + \left( {2 + \alpha } \right) {{\left( {\mu + \alpha \mu } \right) }^{ - 1}}} \right] }^{y + 2}}}}} \right\} ,\nonumber \\&\quad y = 0,1,2,\ldots , \end{aligned}$$
(5)

where\(\alpha >0\)and\(\mu >0\). The mean and variance of5 are given by, respectively,

$$\begin{aligned} \begin{array}{l} E\left( Y \right) = \mu , \\ {\mathrm{Var}}\left( Y \right) = \underbrace{\mu }_{\text {I}} + \underbrace{\frac{{{\mu ^2}}}{{{{\left( {2 + \alpha } \right) }^2}}}\left( {2 + 4\alpha + {\alpha ^2}} \right) }_{\text {II}}. \end{array} \end{aligned}$$
(6)

Note that the parameter \(\alpha\) should be greater than zero to ensure the positive variance. The other statistical properties of PQL distribution, such as probability and moment generating functions, mode and its cdf, under the above re-parametrization can be obtained following the results in Grine and Zeghdoudi [6]. As seen from 6, since the second part of variance equation for PQL distribution is greater than zero for all values of the parameters \(\alpha\) and \(\mu\), the variance of PQL distribution is always greater than its mean. Therefore, PQL distribution can be a good choice for modeling the over-dispersed data sets.

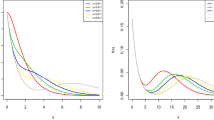
Figure 1 displays the dispersion index and possible shapes of PQL distribution. When the parameters \(\alpha\) and \(\mu\) increase, the dispersion of PX distribution increases. Note that the effect of the parameter \(\mu\) on dispersion is higher than that of parameter \(\alpha\). As seen from left side of Fig. 1, PQL distribution can be a good choice for modeling extremely right-skewed data sets.

Fig. 1
figure 1

The dispersion index (right) and the pmf shapes of PQL distribution (left) for some values of \(\alpha\) and \(\mu\)

Full size image

Generating random variables from Poisson-xgamma distribution

Here, a general algorithm and corresponding code written in R software are given to generate random variables from PQL distribution. The below code can be used for all discrete distributions such as Poisson, Poisson–Lindley, negative-binomial.

figure a

Estimation

In this section, ML and MM estimation methods are considered to estimate the unknown parameters of PQL distribution.

Maximum likelihood estimation

Let \(X_{1},X_{2},\dots ,X_{n}\) be independent and identically distributed \({\text {PQL}}\) random variables. The log-likelihood function is

$$\begin{aligned} \ell \left( {\alpha ,\mu } \right) & = n\ln \left( {\frac{{2 + \alpha }}{{{{\left( {\alpha + 1} \right) }^2}\mu }}} \right) \nonumber \\&+\, \sum \limits _{i = 1}^n {\ln \left[ {\alpha + \left( {2 + \alpha } \right) {{\left( {\mu + \alpha \mu } \right) }^{ - 1}}\left( {{y_i} + \alpha + 1} \right) } \right] } \nonumber \\&-\, \ln \left( {\left[ {1 + \left( {2 + \alpha } \right) {{\left( {\mu + \alpha \mu } \right) }^{ - 1}}} \right] } \right) \sum \limits _{i = 1}^n {\left( {{y_i} + 2} \right) }. \end{aligned}$$
(7)

Taking partial derivatives of (7) with respect to \(\alpha\) and \(\mu\), we have

$$\begin{aligned} \frac{{\partial \ell }}{{\partial \alpha }} & = n{\left( {\alpha + 2} \right) ^{ - 1}}{\left( {\alpha + 1} \right) ^2}\mu \left( {\frac{1}{{{{\left( {\alpha + 1} \right) }^2}\mu }} - \frac{{2\left( {\alpha + 2} \right) }}{{{{\left( {\alpha + 1} \right) }^3}\mu }}} \right) \nonumber \\&-\, {\left( {\frac{{\alpha + 2}}{{\alpha \mu + \mu }} + 1} \right) ^{ - 1}}\left( {\frac{1}{{\alpha \mu + \mu }} - \frac{{\left( {\alpha + 2} \right) \mu }}{{{{\left( {\alpha \mu + \mu } \right) }^2}}}} \right) \nonumber \\&\sum \limits _{i = 1}^n {\left( {{y_i} + 2} \right) } \nonumber \\&+\, \sum \limits _{i = 1}^n \left[ \left( \frac{{\alpha + 2}}{{\alpha \mu + \mu }} + \frac{{\left( {\alpha + 2} \right) \mu \left( {{y_i} + \alpha + 1} \right) }}{{{{\left( {\alpha \mu + \mu } \right) }^2}}} \nonumber \right. \right. \\&\left. \left. + \frac{{\left( {{y_i} + \alpha + 1} \right) }}{{\alpha \mu + \mu }} + 1 \right) \nonumber \right. \\&\left. \left( {\alpha + \frac{{\left( {\alpha + 2} \right) \left( {{y_i} + \alpha + 1} \right) }}{{\alpha \mu + \mu }}} \right) \right] \end{aligned}$$
(8)
$$\begin{aligned} \frac{{\partial \ell }}{{\partial \mu }} & = \sum \limits _{i = 1}^n {\frac{{\left( {\alpha + 1} \right) \left( {\alpha + 2} \right) \left( {{y_i} + 2} \right) }}{{{{\left( {\alpha \mu + \mu } \right) }^2} \left( {\frac{{\alpha + 2}}{{\alpha \mu + \mu }} + 1} \right) }}} \nonumber \\&-\, \sum \limits _{i = 1}^n \frac{{\left( {\alpha + 1} \right) \left( {\alpha + 2} \right) \left( {{y_i} + \alpha + 1} \right) }}{{\left( {\alpha \mu + \mu } \right) }^2}\nonumber \\&\left( {\frac{{\alpha + 2\left( {{y_i} + \alpha + 1} \right) }}{{\alpha \mu + \mu }} + \alpha } \right) - \frac{n}{\mu } \end{aligned}$$
(9)

The ML estimates of \(\left( \alpha ,\lambda \right)\) can be obtained by means of simultaneous solutions of 8 and 9. It is not possible to obtain explicit forms of ML estimates of PQL distribution since the likelihood equations contain nonlinear functions. For this reason, nonlinear minimization tools are needed to solve these equations. The nonlinear minimization (nlm) function of R software is used for this purpose. The corresponding interval estimations of the parameters are obtained by means of observed information matrix which is given by

$$\begin{aligned} {\mathbf{I }}_F(\pmb \tau )=-\left( \begin{array}{cccc} I_{\alpha \alpha } &{} I_{\alpha \mu } \\ I_{\mu \alpha } &{} I_{\mu \mu } \\ \end{array} \right) . \end{aligned}$$

The elements of observed information matrix are upon request from the authors. It is well known that under the regularity conditions that are fulfilled for the parameters, the asymptotic joint distribution of \((\widehat{\alpha },\widehat{\mu })\), as \(n\rightarrow \infty\) is a bi-variate normal distribution with mean \((\alpha ,\mu )\) and variance–covariance \({\mathbf{I }}^{-1}_F(\pmb \tau )\). Using the asymptotic normality, the asymptotic \(100(1-p)\%\) confidence intervals for the parameters \(\alpha\) and \(\mu\), respectively, are given by

$$\begin{aligned} \widehat{\alpha }\pm z_{p/2}\sqrt{\widehat{{\mathrm{Var}}({{\alpha }})}},\quad \widehat{\mu } \pm z_{p/2}\sqrt{\widehat{\mathrm{Var}({\mu })}}, \end{aligned}$$

where \(z_{p/2}\) is the upper p / 2 quantile of the standard normal distribution.

Method of moments

The MM estimators of the parameters \(\alpha\) and \(\mu\) can be obtained by equating the mean and variance of PQL distribution to sample mean and variance, given as follows

$$\begin{aligned}&{\bar{y}} = \mu , \end{aligned}$$
(10)
$$\begin{aligned}&{s^2} = \mu + \frac{{{\mu ^2}}}{{{{\left( {2 + \alpha } \right) }^2}}}\left( {2 + 4\alpha + {\alpha ^2}} \right) , \end{aligned}$$
(11)

where \({\bar{y}}\) and \(s^2\) are the sample mean and variance, respectively. For simultaneous solution of (10) and (11), we have

$$\begin{aligned}&{{\hat{\mu }} _{\mathrm{MM}}} = {\bar{y}}, \end{aligned}$$
(12)
$$\begin{aligned}&{{\hat{\alpha }} _{\mathrm{MM}}} = \sqrt{\frac{{2{{{\bar{y}}}^2}}}{{{{{\bar{y}}}^2} + {\bar{y}} - {s^2}}}} - 2 \end{aligned}$$
(13)

Theorem 1

For fixed values of\(\mu\), MM estimator\({{\hat{\alpha }} _{MM}}\)of\(\alpha\)is consistent and asymptotically normal distributed:

$$\begin{aligned} \sqrt{n} \left( {{\bar{X}} - \mu } \right) \rightarrow N\left( {0,{\upsilon ^2}\left( \theta \right) } \right) , \end{aligned}$$
(14)

where

$$\begin{aligned} {\upsilon ^2}\left( \theta \right) = \frac{{2 + 4\alpha + {\alpha ^2} + \theta \left( {\alpha + 2} \right) \left( {\alpha + 1} \right) }}{{{{\left( {\alpha + 1} \right) }^2}{\theta ^2}}}. \end{aligned}$$
(15)

The detailed information about asymptotic properties of MM estimators can be found in Farbod and Arzideh [4].

Simulation

In this section, Monte Carlo simulation study is conducted to evaluate the finite sample performance of ML and MM estimates of PQL distribution. The following simulation procedure is used.

  1. 1.

    Set the sample size n and the vector of parameters \(\varvec{\theta }=\left( \alpha ,\mu \right) ^T\);

  2. 2.

    Generate random observations from the \({\text {PQL}}\left( {\alpha ,\mu } \right)\) distribution, using the algorithm given in “Generating random variables from Poisson-xgamma distribution” section, with size n;

  3. 3.

    Use the generated random observations in Step 2, and estimate \(\varvec{\theta }\) by means of ML and MM estimation methods;

  4. 4.

    Repeat N times the steps 2 and 3;

  5. 5.

    Use \(\varvec{\hat{\theta }}\) and \(\varvec{\theta }\) and calculate the biases, mean relative estimates (MREs) and mean square errors (MSEs) from the following equations:

    $$\begin{aligned} \begin{array}{l} {\mathrm{Bias}} = \sum \limits _{j = 1}^N {\frac{{{{ { \varvec{{\hat{\theta }}} }_{i,j}}} - { \varvec{\theta }_i}}}{N}},\,\,\,\,{\mathrm{MRE}} = \sum \limits _{j = 1}^N {\frac{{{{{{{{\varvec{{\hat{\theta }}} }}}_{i,j}}} / {{{\varvec{\theta }_i }}}}}}{N}}, \\ {\mathrm{MSE}} = \sum \limits _{j = 1}^N {\frac{{{{\left( {{{{\varvec{\hat{\theta }} }}_{i,j}} - {{\varvec{\theta }_i }}} \right) }^2}}}{N}},\,\,\,\ i=1,2. \end{array} \end{aligned}$$

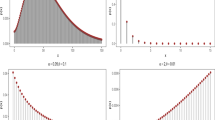
Figure 2 displays results of simulation study performed under the above procedure. The following parameters are considered: \(\varvec{\theta }=\left( \alpha =0.5,\mu =1.5\right) ^T\), \(N=10,000\) and \(n=40,45,50,\ldots ,500\). When n is sufficiently large, MREs should be closer to one and MSEs and biases should be closer to zero. As seen from Fig. 2, when the sample size, n, increases, the MSEs and biases are closer to zero and MREs approach to one for both estimation methods. The MM and ML estimation methods yield similar results for the parameter \(\mu\) in view of estimated MSE, bias and MRE. However, ML estimation method provides more satisfactory results for the parameter \(\alpha,\) especially for small sample sizes. Therefore, we suggest to use ML estimation method when the sample size is small.

Fig. 2
figure 2

Estimated biases, MSEs and MREs of the parameters of PQL distribution based on the ML and MM estimation methods

Full size image

Poisson quasi-Lindley regression model

The Poisson and negative-binomial are the two commonly used regression models for count data modeling. When the response variable is not equi-dispersed, the negative-binomial regression model is preferable. Here, an alternative regression model is introduced for over-dispersed response variable.

Let random variable Y follow a PQL distribution, given in (5). The mean of Y is \(E\left( Y|\alpha ,\mu \right) =\mu\). Therefore, the covariates can be linked to the mean of response variable, y, by means of the log-link function, given by

$$\begin{aligned} {\mu _i} = {\exp \left( {\pmb x_i^T \pmb {\beta } } \right) },i = 1,\ldots ,n, \end{aligned}$$
(16)

where \(\pmb x_i^T = \left( {{x_{i1}},{x_{i2}},\ldots {x_{ik}}} \right)\) is the vector of covariates and \(\pmb {\beta } = {\left( {{\beta _0},{\beta _1},{\beta _2},\ldots {\beta _k}} \right) ^T}\) is the unknown vector of regression coefficients. Inserting (16) in (5), the log-likelihood function can be obtained as follows

$$\begin{aligned} \ell \left( \pmb \tau \right) & = n\ln \left( {2 + \alpha } \right) - \sum \limits _{i = 1}^n {\ln \left[ {{{\left( {\alpha + 1} \right) }^2}\exp \left( {{\pmb {x}}_i^T{\pmb {\beta }}} \right) } \right] } \nonumber \\&+\, \sum \limits _{i = 1}^n \ln \left[ \alpha + \left( {2 + \alpha } \right) \left[ \exp \left( {{\pmb {x}}_i^T{\pmb {\beta }}} \right) \nonumber \right. \right. \\&\left. \left. \quad +\, \alpha \exp \left( {{\pmb {x}}_i^T{\pmb {\beta }}} \right) \right] ^{ - 1}\left( {{y_i} + \alpha + 1} \right) \right] \nonumber \\&-\, \sum \limits _{i = 1}^n \left( {{y_i} + 2} \right) \ln \left[ 1 + \left( {2 + \alpha } \right) \left[ \exp \left( {{\pmb {x}}_i^T{\pmb {\beta }}} \right) \nonumber \right. \right. \\&\left. \left. +\, \alpha \exp \left( {{\pmb {x}}_i^T{\pmb {\beta }}} \right) \right] ^{ - 1} \right] , \end{aligned}$$
(17)

where \(\pmb \tau =\left( \alpha ,\pmb \beta \right) ^T\). The unknown parameters, \(\alpha\) and \(\pmb {\beta } = {\left( {{\beta _0},{\beta _1},{\beta _2},\ldots {\beta _k}} \right) ^T}\), are obtained by maximizing (16) with the nlm function of R software. Under standard regularity conditions, the asymptotic distribution of \((\widehat{\pmb {\tau }}-\pmb {\tau })\) is multivariate normal \(N_{k+2}(0,J(\pmb {\tau })^{-1})\), where \(J(\pmb {\tau })\) is the expected information matrix. The asymptotic covariance matrix \(J(\pmb {\tau })^{-1}\) of \(\widehat{\pmb {\tau }}\) can be approximated by the inverse of the \((k+2)\times (k+2)\) observed information matrix \({I}(\pmb {\tau })\), whose elements are evaluated numerically via most statistical packages. The approximate multivariate normal distribution \(N_{k+2}(0,{I }(\pmb {\tau })^{-1})\) for \(\widehat{\pmb {\tau }}\) can be used to construct asymptotic confidence intervals for the vector of parameters \(\pmb {\tau }\).

Empirical study

In this section, modeling ability of PQL regression model is compared with Poisson and NB regression models via an application on real data set. The data contain number of absence (daily), gender and type of instructional program of the 314 high school students from two urban high schools. The data set can be obtained from https://stats.idre.ucla.edu/stat/stata/dae/nb_data.dta. The response variable, number of absence \(y_i\), is modeled with gender (female = 1, male = 0) \(\left( x_1\right)\) and type of instructional program (general = 1, academic = 2, vocational = 3). The vocational program is used as a baseline category for type of instructional program variable. The general and academic instructional programs are coded as \(x_2\) and \(x_3\), respectively. To decide the best model, the estimated negative log-likelihood value, Akaike Information Criteria (AIC) and Bayesian Information Criteria (BIC) values are used. The lowest values of these statistics show the best-fitted model for the used data set. The following regression model is fitted.

$$\begin{aligned} {\mu _i} = \exp \left( {{\beta _0} + {\beta _1}{x_{1i}} + {\beta _2}{x_{2i}} + {\beta _3}{x_{3i}}} \right) \end{aligned}$$
(18)

Figure 3 displays the distribution of days of absence. The mean of response variable is 5.955, and variance is 49.518 which is an evidence for over-dispersion.

Fig. 3
figure 3

The distribution of days of absence of students

Full size image

Table 1 lists the estimated parameters of the models and corresponding SEs, estimated negative \(-\ell\), AIC and BIC values. Since PQL regression model has the lowest values of these statistics, we conclude that PQL regression model provides better fits than Poisson and NB regression models, especially for over-dispersed data set.

Table 1 The estimated parameters of models and goodness-of-fit statistics
Full size table

The obtained observed information matrix of PQL regression model, \(I\left( \pmb {\tau }\right)\), is

$$\begin{aligned} \left[ {\begin{array}{*{25}{c}} {{\mathrm{269}}{\mathrm{.303}}}\\ {{\mathrm{398}}{\mathrm{.549}}}\\ {{\mathrm{37}}{\mathrm{.894}}}\\ {{\mathrm{151}}{\mathrm{.312}}}\\ {{\mathrm{0}}{\mathrm{.058}}} \end{array}{}\begin{array}{*{20}{c}} {{\mathrm{398}}{\mathrm{.549}}}&{}{{\mathrm{37}}{\mathrm{.894}}}&{}{{\mathrm{151}}{\mathrm{.312}}}&{}{{\mathrm{0}}{\mathrm{.058}}}\\ {{\mathrm{656}}{\mathrm{.873}}}&{}{{\mathrm{53}}{\mathrm{.206}}}&{}{{\mathrm{224}}{\mathrm{.836}}}&{}{{\mathrm{0}}{\mathrm{.117}}}\\ {{\mathrm{53}}{\mathrm{.206}}}&{}{{\mathrm{37}}{\mathrm{.895}}}&{}{{\mathrm{0}}{\mathrm{.001}}}&{}{-\,{\mathrm{0}}{\mathrm{.084}}}\\ {{\mathrm{224}}{\mathrm{.836}}}&{}{{\mathrm{0}}{\mathrm{.001}}}&{}{{\mathrm{151}}{\mathrm{.305}}}&{}{{\mathrm{0}}{\mathrm{.043}}}\\ {{\mathrm{0}}{\mathrm{.117}}}&{}{-\,{\mathrm{0}}{\mathrm{.084}}}&{}{{\mathrm{0}}{\mathrm{.043}}}&{}{{\mathrm{0}}{\mathrm{.382}}} \end{array}} \right] \end{aligned}$$

The diagonal elements of the inverse of \(I\left( \pmb {\tau }\right)\) give the variances of estimated parameters. The inverse of \(I\left( \pmb {\tau }\right)\) is

$$\begin{aligned} \left[ {\begin{array}{*{25}{c}} {{\mathrm{0}}{\mathrm{.046}}}\\ -\,{{\mathrm{0}}{\mathrm{.022}}}\\ -\,{{\mathrm{0}}{\mathrm{.015}}}\\ -\,{{\mathrm{0}}{\mathrm{.013}}}\\ -\,{{\mathrm{0}}{\mathrm{.021}}} \end{array}{\mathrm{}}\begin{array}{*{20}{c}} -\,{{\mathrm{0}}{\mathrm{.022}}}&{}-\,{{\mathrm{0}}{\mathrm{.015}}}&{}-\,{{\mathrm{0}}{\mathrm{.013}}}&{}-\,{{\mathrm{0}}{\mathrm{.021}}}\\ {{\mathrm{0}}{\mathrm{.015}}}&{}{{\mathrm{0}}{\mathrm{.001}}}&{}{{\mathrm{0}}{\mathrm{.001}}}&{}-\,{{\mathrm{0}}{\mathrm{.008}}}\\ {{\mathrm{0}}{\mathrm{.001}}}&{}{{\mathrm{0}}{\mathrm{.039}}}&{}{{\mathrm{0}}{\mathrm{.012}}}&{}{{\mathrm{0}}{\mathrm{.091}}}\\ {{\mathrm{0}}{\mathrm{.001}}}&{}{{\mathrm{0}}{\mathrm{.013}}}&{}{{\mathrm{0}}{\mathrm{.019}}}&{}{{\mathrm{0}}{\mathrm{.025}}}\\ -\,{{\mathrm{0}}{\mathrm{.008}}}&{}{{\mathrm{0}}{\mathrm{.091}}}&{}{{\mathrm{0}}{\mathrm{.025}}}&{}{{\mathrm{26}}{\mathrm{.407}}} \end{array}} \right] \end{aligned}$$

The asymptotic confidence intervals of regression parameters are \(0.049<\beta _1<-0.430\), \(1.349<\beta _2<0.961\) and \(1.215<\beta _3<0.673\), respectively. As seen from estimated regression coefficients of PQL regression model, we conclude that the gender has no statistically significant effect on the days of absence for students. However, the days of absence for general and academic instructional program students are 1.348 and 0.945 times higher than the vocational instructional program students.

Conclusion

A re-parametrization of the Poisson quasi-Lindley distribution is introduced and studied comprehensively. The parameter estimation problem of the Poisson quasi-Lindley distribution is discussed via extensive simulation study. A new regression model for count data is proposed and compared with Poisson and negative-binomial regression models based on the real data set. We conclude that Poisson quasi-Lindley regression model exhibits better fitting performance than Poisson and negative-binomial regression models when the response variable is over-dispersed. We hope that the results given in this study will be very helpful for researchers studying in this field.