Effect of Joule heating on the flow over an exponentially stretching sheet with convective thermal condition

Abstract

This article analyzes the Joule heating effect on the viscous fluid flow over a porous sheet stretching exponentially by employing convective boundary condition. The numerical solutions to the governing equations are obtained using a local similarity and non-similarity approach together with a successive linearization procedure and a Chebyshev collocation method. The influence of the slip parameter, suction/injection parameter, magnetic parameter, Joule heating parameter and Biot number on the velocity, temperature, concentration, skin friction, rate of heat transfer and rate of mass transfer is displayed in graphs. The velocity is found to decay for higher estimation of magnetic parameter, while a thermal field is enhanced for higher Joule heating and Biot number. It is also observed from the investigation that the rate of heat transfer reduces with Joule heating and enhances with increasing Biot number.

Introduction

The investigation of flow over an exponentially stretching sheet is of considerable interest because of its applications in industrial and technological processes, such as fluid film condensation process, aerodynamic extrusion of plastic sheets, crystal growth, cooling process of metallic sheets, design of chemical processing equipment and various heat exchangers, and glass and polymer industries.

After the pioneering work of Sakiadis [1, 2], several researchers investigated the flow due to stretching sheet. Abbas et al. [3] numerically investigated the influence of a Deborah number on the flow of Maxwell fluid over a sheet moving exponentially. The study of convective transport with the interaction of the magnetic field has gained attention of many scientists due to its comprehensive applications in engineering. Several metallurgical processes involve the cooling of continuous strips or filaments such as strengthening and tinning of copper wires, which are sometimes stretched during the process. The proportion of cooling of these strips can be controlled by exposing them to magnetic fields. Similarly, the molten metals can be purified from nonmetallic inclusions by utilizing a magnetic field. Krishnamurthy et al. [4] focused on the flow of a nanofluid over stretching surface moving exponentially by considering magnetic and viscous dissipation effects. Aleng et al. [5] reported the characteristics of heat transfer past a sheet which is shrinking exponentially. Sreedevi et al. [6] examined the influence of Brownian motion, thermophoresis, thermal radiation and chemical reaction on the MHD flow over linear and nonlinear stretching sheets in a nanofluid-saturated porous medium. Nayak et al. [7] focused on the impact of magnetic field and radiation on the free convective flow of nanofluid over a linear stretching sheet. Shateyi and Gerald [8] investigated the mixed convection model for a magnetohydrodynamic Jeffery fluid flowing over an exponentially stretching sheet. Kumar et al. [9] studied the flow, thermal and concentration boundary layer nature of Casson and Carreau fluids over an exponential stretching surface with zero normal flux of nanoparticles having magnetic behavior. Jusoh et al. [10] reported the magnetohydrodynamic effect on three-dimensional rotating flow and heat transfer of ferrofluid over an exponentially permeable stretching/shrinking sheet with suction. For more details, one can refer to [11,12,13].

The Joule heating is produced by intercommunication among the atomic ions that compose the body of the conductor and moving charged particles that form the current. It is a result of the impingement between the moving particles. In this procedure, a percentage of the kinetic energy is changed over into the heat and subsequently temperature of the body enhances. Examples include: An incandescent light bulb glows when the filament is heated by Joule heating, the filament gets so hot that it glows white with thermal radiation. This is also called blackbody radiation. Electric stoves and other electric heaters, soldering irons, cartridge heaters, electric fuses, electronic cigarettes, thermistors and food processing equipment are practical uses of Joule heating. In recent years, the engineers and researchers are intrigued to build the effectiveness of different mechanical frameworks and industrial machineries. Such sorts of challenges can be taken care of to diminish the temperature created because of ohmic dissipation. Several researchers explored the impact of Joule heating on fluid flow and heat transfer at different conditions and found that it plays a prominent impact on MHD flows. Jat and Gopi [14] analyzed the influence of Joule heating and radiation on MHD flow of viscous fluid over a sheet elongating exponentially. Yadav and Sharma [15] investigated the effect of Joule heating on MHD flow due to exponentially moving stretching sheet in porous media. Rao et al. [16] reported the heat and mass transfer characteristics of a nanofluid over an exponentially stretching sheet in the presence of Joule heating. Adeniyan and Adigun [17] reported that an increase in the value of Eckert number increases the thickness of the thermal boundary layer. Srinivasacharya and Jagadeeshwar [18] analyzed the Hall current and Joule heating effects on the flow of viscous fluid past a sheet stretching exponentially. Muhammad et al. [19] investigated the nonlinear thermal radiation, viscous dissipation and Joule heating effects on the flow due to nonlinear stretching surface with variable thickness. Hayat et al. [20,21,22,23] explored the impact of Joule heating on the radiative flow of viscous fluid over a stretching cylinder, rotating disk and stretching surface, respectively. Khan et al. [24,25,26] addressed the entropy generation in radiative motion of tangent hyperbolic nanofluid in the presence of activation energy, nonlinear mixed convection and Joule heating effect. It is noticed from their investigation that the entropy generation rate enhances with increasing Eckert number and magnetic parameter while the opposite behavior is noticed for Reynolds number. It is also witnessed that for larger values of Eckert number the temperature of the fluid is increasing.

Generally accepted boundary condition on the solid surface is no-slip condition. However, Navier [27] suggested that fluid slips at the solid boundary and slip velocity depend linearly on the shear stress. The fluid slippage phenomenon at the solid boundary appears in numerous applications, for example, in nanochannels or microchannels and the cleaning of simulated heart valves and internal cavities. Using this velocity slip conditions, Su and Zheng [28] reported the heat transfer of nanofluids over a stretching wedge by taking Joule heating and Hall effect into consideration. On the other hand, a novel technique for the heating process, by providing the heat with finite capacity to the convecting fluid through the bounding surface, has been attracted by numerous researchers. This type of thermal boundary condition, called a convective boundary condition, states that the rate of exchange of heat across the boundary is proportional to the difference in local temperature with the ambient conditions [29]. Due to the realistic nature of the convective thermal condition, the investigation of heat transfer with this condition has rich significance in mechanical and designing fields, for example, heat exchangers, atomic plants, gas turbines and so forth. With this boundary condition, Gideon and Abah [30] considered the double-diffusive stagnation-point flow in a porous medium with magnetic effects. Mustafa et al. [31] reported the impact of convective thermal condition in the nanofluid flow past a stretching sheet by considering the Brownian motion and thermophoresis effects. Hayat et al. [32] analyzed the heat transfer process in a steady MHD flow of viscous nanofluid due to a permeable exponentially stretching surface with convective boundary conditions. Rahman et al. [33] considered the steady flow and thermal flow of nanofluid past an exponentially shrinking surface with convective thermal conditions. Mabood et al. [34] analyzed the stagnation-point flow and heat transport over an exponentially stretching sheet. Khan et al. [35] studied the boundary layer flow of nanofluid past a bidirectional exponentially stretching sheet with the convective thermal condition. Recently, Srinivasacharya and Jagadeeshwar et al. [36] reported that the increase in the Biot number increases the heat transfer from the sheet to the fluid.

The objective of the present work is to examine the influence of Joule heating and velocity slip on the convective flow of a viscous fluid over an exponentially stretching permeable sheet.

Mathematical formulation

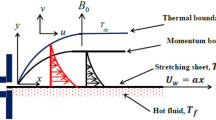
Consider a stretching sheet in a laminar slip flow of viscous incompressible fluid with a temperature T_∞ and concentration C_∞. The $\tilde{x}$- and $\tilde{y}$-axes of the Cartesian framework are taken along and orthogonal to the sheet, respectively, as shown in Fig. 1. The stretching velocity of the sheet is assumed as $U_{*} (\tilde{x}) = U_{0} e^{{\tilde{x}/L}}$, where $\tilde{x}$ is the distance from the slit, L is the scaling parameter and U₀ is the reference velocity. Assume that the sheet is either cooled or heated convectively through a fluid with a temperature T_f, which induces a variable heat transfer coefficient h_f, where $h_{\text{f}} = h\sqrt {U_{0} /2L} e^{{\tilde{x}/2L}}$ and h is constant. A magnetic field $B(\tilde{x}) = B_{0} e^{{\tilde{x}/2L}}$, where B₀ is the constant magnetic field, is applied orthogonal to the sheet. The magnetic Reynolds number is very small so that the induced magnetic field is neglected. ($\tilde{u}_{x}$, $\tilde{u}_{y}$) is the velocity vector, $\tilde{C}$ is the concentration and $\tilde{T}$ is the temperature. The suction/injection velocity of the fluid through the sheet is $V_{*} (\tilde{x}) = V_{0} e^{{\tilde{x}/2L}}$, where V₀ is the strength of suction/injection. Further, the slip velocity of the fluid is assumed as $N(\tilde{x}) = N_{0} e^{{ - \tilde{x}/2L}}$, where N₀ is the velocity slip factor. Hence, the following are the equations [37, 38] which govern the present flow

$$\frac{{\partial \tilde{u}_{x} }}{{\partial \tilde{x}}} + \frac{{\partial \tilde{u}_{y} }}{{\partial \tilde{y}}} = 0,$$

(1)

$$\tilde{u}_{x} \frac{{\partial \tilde{u}_{x} }}{{\partial \tilde{x}}} + \tilde{u}_{y} \frac{{\partial \tilde{u}_{x} }}{{\partial \tilde{y}}} = \nu \frac{{\partial^{2} \tilde{u}_{x} }}{{\partial \tilde{y}^{2} }} - \frac{{\sigma B^{2} }}{\rho }\tilde{u}_{x} ,$$

(2)

$$\tilde{u}_{x} \frac{{\partial \tilde{T}}}{{\partial \tilde{x}}} + \tilde{u}_{y} \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} = \alpha \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }} + \frac{{\sigma B^{2} }}{{\rho c_{p} }}\tilde{u}_{x}^{2} ,$$

(3)

$$\tilde{u}_{x} \frac{{\partial \tilde{C}}}{{\partial \tilde{x}}} + \tilde{u}_{y} \frac{{\partial \tilde{C}}}{{\partial \tilde{y}}} = D\frac{{\partial^{2} \tilde{C}}}{{\partial \tilde{y}^{2} }},$$

(4)

where D, α(= $\kappa$/ρc_p), ρ, υ and c_p are mass diffusivity of the medium, thermal diffusivity, density, kinematic viscosity and specific heat capacity at the constant pressure, respectively.

Fig. 1

Physical model and coordinate system

The conditions on the surface of the sheet are as follows:

$$\left. {\begin{array}{*{20}l} {\tilde{u}_{x} = U_{*} + N\nu \frac{{\partial \tilde{u}_{x} }}{{\partial \tilde{y}}},\tilde{u}_{y} = - V_{*} (\tilde{x}),h_{\text{f}} (T_{\text{f}} - \tilde{T}) = - \kappa \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}},\tilde{C} = C_{w} \quad {\text{at}}\quad \tilde{y} = 0} \hfill \\ {\tilde{u}_{x} \to 0,\tilde{T} \to T_{\infty } ,\tilde{C} \to C_{\infty } \;\;{\text{as}}\quad \tilde{y} \to \infty } \hfill \\ \end{array} } \right\}.$$

(5)

Introducing the stream functions through $\tilde{u}_{x} = - \frac{\partial \psi }{{\partial \tilde{y}}}\;\;{\text{and}}\;\;\tilde{u}_{y} = \frac{\partial \psi }{{\partial \tilde{x}}}$ and then the following dimensionless variables

$$\left. {\begin{array}{*{20}l} {\tilde{x} = xL,\;\tilde{y} = y\sqrt {\frac{2\nu L}{{U_{0} }}} e^{{\frac{{ - \tilde{x}}}{2L}}} ,\;\;\psi = \sqrt {2\nu LU_{0} } e^{{\frac{{\tilde{x}}}{2L}}} F(x,y),} \hfill \\ {\tilde{T} = T_{\infty } + (T_{\text{f}} - T_{\infty } )T(x,y),\;\;\tilde{C} = C_{\infty } + (C_{w} - C_{\infty } )C(x,y)} \hfill \\ \end{array} } \right\}$$

(6)

into Eqs. (1)–(4), we obtain

$$F^{\prime\prime\prime} - 2F^{{{\prime }2}} + FF^{\prime\prime} + 2\left( {\frac{\partial F}{\partial x}F^{\prime\prime} - \frac{{\partial F^{\prime}}}{\partial x}F^{\prime}} \right) - H_{\text{a}} F^{\prime} = 0,$$

(7)

$$\frac{1}{Pr}T^{\prime\prime} + FT^{\prime} + J\;e^{2x} \;F^{{{\prime }2}} + 2\left( {\frac{\partial F}{\partial x}T^{\prime} - \frac{\partial T}{\partial x}F^{\prime}} \right) = 0,$$

(8)

$$\frac{1}{Sc}C^{\prime\prime} + FC^{\prime} + 2\left( {\frac{\partial F}{\partial x}C^{\prime} - \frac{\partial C}{\partial x}F^{\prime}} \right) = 0,$$

(9)

where the prime denotes differentiation with respect to y, Pr = υ/α is the Prandtl number, Sc = υ/D is the Schmidt number, $S = V_{0} \sqrt {2L/\nu U_{0} }$ is the suction/injection parameter according to S >0 or S <0, respectively, $\lambda = N_{0} \sqrt {\nu U_{0} /2L}$ is the velocity slip parameter, Bi = h$\sqrt \nu /\kappa$ is the Biot number, $\kappa$ is the thermal conductivity of the fluid, $J = 2L\sigma B_{0}^{2} U_{0} /rc_{\text{p}} \left( {T_{\text{f}} - T_{\infty } } \right)$ is the Joule heating parameter and $H_{\text{a}} = 2L\sigma B_{0}^{2} /\rho U_{0}$ is the magnetic parameter.

The transformed boundary conditions are as follows:

$$\left. {\begin{array}{*{20}l} {F(x,0) + 2\frac{\partial F}{\partial x}(x,0) = S,\;\;F^{\prime}(x,0) = 1 + \lambda F^{\prime\prime}(x,0),\;\;T^{\prime}(x,0) = - Bi(1 - T(x,0)),C(x,0) = 1} \hfill \\ {F^{\prime}(x,y) \to 0,T(x,y) \to 0,C(x,y) \to 0\;\;{\text{as}}\quad y \to \infty } \hfill \\ \end{array} } \right\}.$$

(10)

The non-dimensional skin friction $C_{\text{f}} = \frac{{2\tau_{\omega } }}{{\rho U_{*}^{2} }}$, the local Nusselt number $Nu_{{\tilde{x}}}$ = $\tilde{x}q_{\text{w}} /\kappa \left( {T_{\text{f}} - T_{\infty } } \right)$ and local Sherwood number $Sh_{{\tilde{x}}}$ = $\tilde{x}q_{\text{m}} /\kappa \left( {C_{\text{w}} - C_{\infty } } \right)$ are given by

$$\begin{aligned} &\sqrt {\frac{L}{2x}} \sqrt {\text{Re}_{x} } \;C_{\text{f}} = F^{\prime\prime}(x,0),\quad \sqrt {\frac{2}{Lx}} \frac{{Nu_{x} }}{{\sqrt {\text{Re}_{x} } }} = - T^{\prime}(x,0)\\&\quad {\text{and}}\quad \sqrt {\frac{2}{Lx}} \frac{{Sh_{x} }}{{\sqrt {\text{Re}_{x} } }} = - C^{\prime}(x,0), \end{aligned}$$

(11)

where $\text{Re}_{{\tilde{x}}}$ = $\tilde{x}$$U_{*} (\tilde{x})/\upsilon$ is the local Reynolds number.

Numerical solution discussion

The numerical solutions to Eqs. (8)–(11) together with Eq. (12) are evaluated using a local similarity and non-similarity method [39, 40], successive linearization and then pseudo-spectral method [41, 42].

Local non-similarity method

The initial approximate solution can be obtained from the local similarity equations for a particular case x < < 1 by suppressing the terms x(∂/∂x). As there are no terms accompanied with x(∂/∂x) in (8)–(11), there is no change in the governing equations and boundary conditions.

In the second step, substitute G = ∂F/∂x, H = ∂T/∂x and K = ∂C/∂x to get back the suppressed terms in the first step. Thus, the second-level truncation is given as follows:

$$F^{\prime\prime\prime} + FF^{\prime\prime} - 2F^{{{\prime }2}} + 2\left( {F^{\prime\prime}G - F^{\prime}G^{\prime}} \right) - H_{\text{a}} F^{\prime} = 0,$$

(12)

$$\frac{1}{Pr}T^{\prime\prime} + FT^{\prime} + J\;e^{2x} F^{{{\prime }2}} + 2\left( {T^{\prime}G - F^{\prime}H} \right) = 0,$$

(13)

$$\frac{1}{Sc}C^{\prime\prime} + FC^{\prime} + 2\left( {C^{\prime}G - F^{\prime}K} \right) = 0.$$

(14)

The corresponding conditions on the boundary are given as follows:

$$\left. {\begin{array}{*{20}l} {F(x,0) + 2G(x,0) = S,F^{\prime}(x,0) = 1 + \lambda F^{\prime\prime}(x,0),T^{\prime}(x,0) = - Bi(1 - T(x,0)),C(x,0) = 1} \hfill \\ {F^{\prime}(x,\infty ) \to 0,T(x,\infty ) \to 0,C(x,\infty ) \to 0} \hfill \\ \end{array} } \right\}.$$

(15)

In the third step, differentiate Eqs. (12)–(14) with respect to x and neglect terms accompanied with ∂G/∂x, ∂H/∂x and ∂K/∂x to get

$$G^{\prime\prime\prime} + FG^{\prime\prime} + GF^{\prime\prime} - 4F^{\prime}G^{\prime} + 2\left( {GG^{\prime\prime} - G^{{{\prime }2}} } \right) - H_{\text{a}} G^{\prime} = 0,$$

(16)

$$\frac{1}{Pr}H^{\prime\prime} + (FH^{\prime} + GT^{\prime}) + 2J\;e^{2x} \left( {F^{{{\prime }2}} + F^{\prime}G^{\prime}} \right) + 2\left( {H^{\prime}G - G^{\prime}H} \right) = 0,$$

(17)

$$\frac{1}{Sc}K^{\prime\prime} + (FK^{\prime} + GC^{\prime}) + 2\left( {K^{\prime}G - G^{\prime}K} \right) = 0.$$

(18)

The associated conditions on the surface are as follows:

$$\left. {\begin{array}{*{20}l} {G(x,0) = 0,G^{\prime}(x,0) = \lambda \;G^{\prime\prime}(x,0),H^{\prime}(x,0) = Bi\;H(x,0),K(x,0) = 0} \hfill \\ {G^{\prime}(x,\infty ) \to 0,H(x,\infty ) \to 0,K(x,\infty ) \to 0} \hfill \\ \end{array} } \right\}.$$

(19)

Successive linearization

The successive linearization method (SLM) is proposed and developed by Motsa and Sibanda [42] and Makukula et al. [43]. This is used to linearize the nonlinear governing equations by taking the approximate solution as a series. The iteration scheme is obtained by linearizing the nonlinear component of a differential equation. The resultant linearized equations are solved by applying any of the numerical method. Here, the Chebyshev collocation method is used to solve linearized equations. The advantage of Chebyshev collocation method is the derivative can be written in the form of a matrix and implementation of the boundary conditions is easy. This technique has been shown by comparison with numerical techniques that it is accurate and gives rapid convergence

$$\begin{aligned} {\text{Let}}\;\varGamma (y)& = \left[ {F,T,C,G,H,K} \right]\;{\text{and}}\;{\text{assume}}\;{\text{that}}\;\\ \varGamma (y) &= \varGamma_{i} (y) + \sum\limits_{r = 0}^{i - 1} {\varGamma_{r} (y)} , \end{aligned}$$

(20)

where Г_i(y) (i = 1, 2, 3, …) are unknown functions that are determined by recursively evaluating the linearized version of (12)–(19) after substituting Eq. (20) into them and Г_r(y) (r ≥ 1) are known functions determined from previous iterations.

$$\begin{aligned} &F_{i} ''' + \chi_{11,i - 1} F_{i} '' + \chi_{12,i - 1} F_{i} ' + \chi_{13,i - 1} F_{i} + \chi_{14,i - 1}\\& \quad G_{i} ' + \chi_{15,i - 1} G_{i} = \zeta_{1,i - 1} , \end{aligned}$$

(21)

$$\chi_{21,i - 1} F_{i} ' + \chi_{22,i - 1} F_{i} + T_{i} '' + \chi_{23,i - 1} T_{i} ' + \chi_{24,i - 1} G_{i} + \chi_{25,i - 1} H_{i} = \zeta_{2,i - 1} ,$$

(22)

$$\chi_{31,i - 1} F_{i} ' + \chi_{32,i - 1} F_{i} + C_{i} '' + \chi_{33,i - 1} C_{i} ' + \chi_{34,i - 1} G_{i} + \chi_{35,i - 1} K_{i} = \zeta_{3,i - 1} ,$$

(23)

$$\begin{aligned} &\chi_{41,i - 1} F_{i} '' + \chi_{42,i - 1} F_{i} ' + \chi_{43,i - 1} F_{i} + G_{i} ''' + \chi_{44,i - 1}\\& \quad G_{i} '' + \chi_{45,i - 1} G_{i} ' + \chi_{46,i - 1} G_{i} = \zeta_{4,i - 1} , \end{aligned}$$

(24)

$$\begin{aligned}& \chi_{51,i - 1} F_{i} ' + \chi_{52,i - 1} F_{i} + \chi_{53,i - 1} T_{i} ' + \chi_{54,i - 1} G_{i} ' + \chi_{55,i - 1}\\&\quad G_{i} + H_{i} '' + \chi_{56,i - 1} H_{i} ' + \chi_{57,i - 1} H_{i} = \zeta_{5,i - 1} , \end{aligned}$$

(25)

$$\begin{aligned} &\chi_{61,i - 1} F_{i} + \chi_{62,i - 1} C_{i} ' + \chi_{63,i - 1} G_{i} ' + \chi_{64,i - 1} G_{i} + K_{i} '' \\& \quad+ \chi_{65,i - 1} K_{i} ' + \chi_{66,i - 1} K_{i} = \zeta_{6,i - 1} , \end{aligned}$$

(26)

where the coefficients $\chi_{lk,n - 1}$ and $\zeta_{k,i - 1}$ (l, k = 1, 2, 3,…, 6) are in terms of the approximations F_i, T_i and C_i (i = 1,2,3,…, n − 1) and their derivatives.

Chebyshev collocation method

The linearized equations obtained in Sect. (3.2) are solved using the Chebyshev collocation procedure [44]. In view of numerical computations, the region [0, ∞) is truncated to [0, L] for large L. In order to apply Chebyshev collocation procedure, the interval [0, L] is converted to [− 1, 1] by the mapping

$$\tilde{\tau } + 1 = 2y/L, \, - 1 \, \le \tilde{\tau } \le \, 1.$$

(27)

The unknown functions Г_i(y) (i = 1, 2, 3, …) and their derivatives are expressed in terms of Chebyshev polynomials $\varUpsilon_{k} (\tilde{\tau }) = \cos (k\cos^{ - 1} (\tilde{\tau }))$ at Gauss–Lobatto collocation points $\tilde{\tau }_{m}$ = cos(πm/ ${\mathfrak{K}}$), m = 0, 1, 2, …, ${\mathfrak{K}}$ as

$$\varGamma_{i} (\tilde{\tau }) = \sum\limits_{k = 0}^{N} {\varGamma_{i} } (\tilde{\tau }_{k} )\varUpsilon_{k} (\tilde{\tau }_{m} )\quad {\text{and}}\quad \frac{{{\text{d}}^{{\mathbf{a}}} \varGamma_{r} }}{{{\text{d}}y^{{\mathbf{a}}} }} = \sum\limits_{k = 0}^{N} {{\mathbf{D}}_{{{\mathbf{km}}}}^{{\mathbf{a}}} } \varGamma_{i} (\tilde{\tau }_{k} ),$$

(28)

where ${\mathbf{D}}$ = 2 ${\mathcal{D}}$ /L with ${\mathcal{D}}$ is the Chebyshev derivative matrix and ${\mathbf{a}}$ is the order of the derivative. Substitution of Eq. (28) into Eqs. (21)–(26) gives

$${\mathbb{A}}_{i - 1} {\mathbb{X}}_{i} = {\mathbb{R}}_{i - 1} ,$$

(29)

where ${\mathbb{A}}_{i - 1}$ is a sixth-order square matrix with elements as (${\mathfrak{K}}$+1)th-order square matrices in terms of the coefficients $\chi_{ij}^{'}$s. ${\mathbb{X}}_{i}$ and ${\mathbb{R}}_{i - 1}$ are the sixth-order column vectors with (${\mathfrak{K}}$+1)X1 column vectors as elements in terms of $\varGamma_{i} (\tilde{\tau }_{k} )$ and $\chi_{s,i - 1}$. Hence, the solution can be obtained by solving the matrix system (29), after implementing the boundary conditions.

Results and discussion

In order to validate accuracy and reliability of the method used, the results for particular values of $S,$$\lambda ,$$H_{a} ,$$x,$$J$ and $Bi$ large are compared with the results obtained by Magyari and Keller [37] and found to be in good agreement with results, as given in Table 1.

Table 1 Comparative analysis of the Nusselt number calculated by the present method for $x = 0$, $J = 0$, $H_{\text{a}} = 0$, $S = 0$, $\lambda = 0$ and $Bi \to \infty$

The numerical calculations are done by taking Sc =0.22, H_a=1.0, S =0.5, Pr =1.0, J =0.2, λ =1.0, x =0.3, Bi =1.0, N =100 and L =20 unless otherwise mentioned.

The influence of slip parameter λ on the velocity, skin friction, temperature, concentration and rate of mass transfer is shown in Fig. 2a–f. It is evident from Fig. 2a, b that an increase in slip parameter diminishes the fluid velocity while skin friction enhances. This trend is seen due to the fact that the fluid velocity near the sheet is no longer equal to velocity of stretching sheet as slip occurs at wall. In addition, the pulling of stretching sheet can be only partly transmitted to the fluid. Figure 2c, d shows that the temperature and rate of heat transfer are increasing with λ. Concentration of the fluid is increasing and the rate of mass transfer is diminishing with an enhancement in λ as shown in Fig. 2e, f. Also, for lower values of slip parameter heat absorption is taking place far away the sheet. In the absence of slip parameter, there is a maximum mass transfer from the sheet to the fluid. Further, there is no impact of x on rate of mass transfer.

Fig. 2

Effect of λ on aF’, bF’’(x,0), cT, d − T’(x,0), eC and f − C’(x,0)

The variation of F’, F’’(x,0), T, − T’(x,0), C and − C’(x,0) with suction/injection parameter S is displayed in Fig. 3a–f. It is demonstrated from Fig. 3a that F’ is diminishing with an increase in S (S >0), while a reverse trend is noticed for injection (S <0). The physical explanation for such a behavior is that while stronger blowing is provided, the heated fluid is pushed farther from the wall where the buoyancy forces can act to accelerate the flow with less influence of the viscosity. This effect acts to increase the shear by increasing the maximum velocity within the boundary layer. The same principle operates but in reverse direction in case of suction. It is depicted from Fig. 3b that F’’(x,0) decreases with an enhancement in the value of suction parameter. Figure 3c displays that the temperature profile reduces with an increment in the value of suction parameter and increases with an increase in the value of injection parameter. In case of suction, the fluid at ambient conditions is brought closer to the surface and reduces the thermal boundary layer thickness. The same principle operates but in reverse direction in case of injection. The reverse trend is observed on the rate of heat transfer as shown in Fig. 3d. Therefore, there is a maximum heat transfer from the sheet to the fluid. Figure 3e, f shows the variation of concentration and rate of mass transfer from the sheet to the fluid. It is obvious from the figures that the same observations may be seen as that of temperature and rate of heat transfer.

Fig. 3

Effect of S on aF’, bF’’(x,0), cT, d − T’(x,0), eC and f − C’(x,0)

The fluctuations of velocity, skin friction, temperature, rate of heat transfer, concentration and rate of mass transfer with H_a are presented in Fig. 4a–f. Due to magnetic field effect, both the velocity and skin friction are decreased. Application of a magnetic field to an electrically conducting fluid produces a kind of drag-like force called Lorentz force. This force causes a reduction in the fluid velocity within the boundary layer as the magnetic field opposes the transport phenomena. Figure 4c, d shows that the temperature slightly enhances and the rate of heat transfer reduces with an increase in the value of H_a. The effect of Lorentz force on velocity profiles generated a kind of friction on the flow, and this friction in turn generated more heat energy which eventually increases the temperature distribution in the flow. On the other hand, in the absence of magnetic field maximum heat exchange is taking place. Figure 4e, f depicts that the concentration is enhanced and the rate of mass transfer reduced with the increase in the value of H_a. Finally, it is noticed that the rate of heat transfer is reduced with an increase in x.

Fig. 4

Effect of H_a on aF’, bF’’(x,0), cT, d − T’(x,0), eC and f − C’(x,0)

The effect of Joule heating parameter J on temperature and the rate of heat transfer is presented in Fig. 5a, b. Temperature profile is slightly increased and the rate of heat transfer is decreased with an increase in the value of J. Due to inside friction of molecules, the mechanical energy converted into thermal energy is responsible for temperature enhancement and reduction in heat transfer rate. It is observed that, in the absence of Joule heating parameter (J = 0), there is no effect of non-similar variable x on the rate of heat transfer and maximum heat transfer occurs. Figure 6a, b shows the variation of temperature and rate of heat transfer with Biot number Bi. It is obvious that the temperature is increasing with the increase in Biot number. For larger values of Bi, Eq. (10) implies T(0) → 1 which is clearly shown in Fig. 6a. Increasing the value of Biot number, the heat transfer coefficient is enhanced predominantly on the surface due to the strong convection as shown in Fig. 6b. Further, the rate of heat transfer is slightly reduced with x.

Fig. 5

Effect of J on aT and b − T’(x,0)

Fig. 6

Effect of Bi on aT and b − T’(x,0)

Conclusions

The flow over a sheet stretching exponentially by considering the Joule heating effects is investigated numerically by employing velocity slip, suction/injection and thermal convective boundary condition. A local similarity and non-similarity method along with successive linearization and Chebyshev collocation method is used to solve the governing equations. The main findings are listed as follows:

• Velocity is diminishing as the values of velocity slip parameter, magnetic parameter and suction parameter are increasing, while it is decreasing with increase in fluid injection at the stretching surface.

• The skin friction coefficient is rising with an enhancement in velocity slip parameter λ and decreasing with an enhancement in the values of suction/injection parameter S and magnetic parameter H_a.

• The temperature increased with a rise in the values of Joule heating parameter J, Biot number Bi, magnetic parameter H_a and velocity parameter λ, while it decreased with larger fluid suction.

• Concentration of the fluid enhanced with an increase in the value of λ and H_a and reduced with an increase in fluid suction at the stretching surface.

• Rate of heat transfer enhances with an enhancement in the values of velocity slip fluid suction parameters and Biot number, while it decreases with an increase in the values Joule heating and magnetic parameters.

• The rate of mass transfer enhances with an enhancement in fluid suction and diminishes with an increase in the value of velocity and magnetic parameters.