Abstract
In this paper, we develop a new hybrid conjugate gradient method that inherits the features of the Liu and Storey (LS), Hestenes and Stiefel (HS), Dai and Yuan (DY) and Conjugate Descent (CD) conjugate gradient methods. The new method generates a descent direction independently of any line search and possesses good convergence properties under the strong Wolfe line search conditions. Numerical results show that the proposed method is robust and efficient.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In this paper, we consider solving the unconstrained optimization problem
where \(x \in {\mathbb {R}}^n\) is an n-dimensional real vector and \(f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a smooth function, using a nonlinear conjugate gradient method. Optimization problems arise naturally in problems from many scientific and operational applications (see e.g. [12, 19,20,21,22, 35, 36], among others).
To solve problem (1), a nonlinear conjugate gradient method starts with an initial guess, \(x_{0}\in {\mathbb {R}}^n\), and generates a sequence \(\{x_{k}\}_{k=0}^{\infty }\) using the recurrence
where the step size \(\alpha _{k}\) is a positive parameter and \(d_{k}\) is the search direction defined by
The scalar \(\beta _{k}\) is the conjugate gradient update coefficient and \(g_{k}=\nabla f(x_{k})\) is the gradient of f at \(x_{k}.\) In finding the step size \(\alpha _{k},\) the inexpensive line searches such as the weak Wolfe line search
the strong Wolfe line search
or the generalized Wolfe conditions
where \(0< \delta< \sigma <1\) and \(\sigma _{1}\ge 0\) are constants, are often used. Generally, conjugate gradient methods differ by the choice of the coefficient \(\beta _{k}.\) Well-known formulas for \(\beta _{k}\) can be divided into two categories. The first category includes Fletcher and Reeves (FR) [11], Dai and Yuan (DY) [6] and Conjugate Descent (CD) [10]:
where \(\Vert \cdot \Vert\) denotes the Euclidean norm and \(y_{k-1}=g_{k}-g_{k-1}.\) These methods have strong convergence properties. However, since they are very often susceptible to jamming, they tend to have poor numerical performance. The other category includes Hestenes and Stiefel (HS) [16], Polak-Ribi\(\grave{\text {e}}\)re-Polyak (PRP) [28, 29] and Liu and Storey (LS) [26]:
Although these methods may fail to converge, they have an in-built automatic restart feature which helps them avoid jamming and hence makes them numerically efficient [5].
In view of the above stated drawbacks and advantages, many researchers have proposed hybrid conjugate gradient methods that combine different \(\beta _{k}\) coefficients so as to limit the drawbacks and maximize in the advantages of the original respective conjugate gradient methods. For instance, Touati-Ahmed and Storey [31] suggested one of the first hybrid method where the coefficient \(\beta _{k}\) is given by
The authors proved that \(\beta _{k}^{TS}\) has good convergence properties and numerically outperforms both the \(\beta _{k}^{FR}\) and \(\beta _{k}^{PRP}\) methods. Alhawarat et al. [3] introduced a hybrid conjugate gradient method in which the conjugate gradient update coefficient is computed as
where \(\mu _{k}\) is defined as
The authors proved that the method possesses global convergence property when weak Wolfe line search is employed. Moreover, numerical results demonstrate that the proposed method outperforms both the CG-Descent 6.8 [14] and CG-Descent 5.3 [13] methods on a number of benchmark test problems.
In [5], Babaie-Kafaki gave a quadratic hybridization of \(\beta _{k}^{FR}\) and \(\beta _{k}^{PRP}\), where
and the hybridization parameter \(\theta ^{\pm }_{k}\) is taken from the roots of the quadratic equation
that is
and
Thus, the author suggested two methods \(\beta _{k}^{HQ+}\) and \(\beta _{k}^{HQ-}\), corresponding to \(\theta ^{+}\) and \(\theta ^{-},\) respectively, with numerical results showing \(\beta _{k}^{HQ-}\) to be more efficient than \(\beta _{k}^{HQ+}\).
More recently, Salih et al. [30] presented another hybrid conjugate gradient method defined by
The authors showed that the \(\beta _{k}^{YHM}\) method satisfies the sufficient descent condition and possesses global convergence property under the strong Wolfe line search. In 2019, Faramarzi and Amini [9] introduced a spectral conjugate gradient method defined as
with the spectral search direction given as
where
with r and D being positive constants. The authors suggested computing the spectral parameter \(\theta _{k}\) as
or
where \(\eta\) and \(\tau\) are constants such that \(\frac{1}{4}+\eta \le \theta _{k}\le \tau ,\)
and
Convergence of this method is established under the strong Wolfe conditions. For more conjugate gradient methods, the reader is referred to the works of [1, 2, 8, 15, 17, 18, 23,24,25, 27, 32, 33].
In this paper, we suggest another new hybrid conjugate gradient method that inherits good computational efforts of \(\beta _{k}^{LS}\) and \(\beta _{k}^{HS}\) methods and also nice convergence properties of \(\beta _{k}^{DY}\) and \(\beta _{k}^{CD}\) methods. This proposed method is presented in the next section, and the rest of the paper is structured as follows. In Sect. 3, we show that the proposed method satisfies the descent condition for any line search and also present its global convergence analysis under the strong Wolfe line search. Numerical comparison with respect to performance profiles of Dolan-Morè [7] and conclusion is presented in Sects. 4 and 5, respectively.
A new hybrid conjugate gradient method
In [32], a variant of the \(\beta _k^{PRP}\) method is proposed, where the coefficient \(\beta _{k}\) is computed as
This method inherits the good numerical performance of the PRP method. Moreover, Huang et al. [17] proved that the \(\beta _k^{WYL}\) method satisfies the sufficient descent property and established that the method is globally convergent under the strong Wolfe line search if the parameter \(\sigma\) in (5) satisfies \(\sigma < \frac{1}{4}.\) Yao et al. [34] extended this idea to the \(\beta _k^{HS}\) method and proposed the update
The authors proved that the method is globally convergent under the strong Wolfe line search with the parameter \(\sigma <\frac{1}{3}\). In Jian et al. [18], a hybrid of \(\beta _{k}^{DY}, \beta _{k}^{FR}, \beta _{k}^{WYL}\ {\text {and}}\ \beta _{k}^{YWH}\) is proposed by introducing the update
with
Independent of the line search, the method generates a descent direction at every iteration. Furthermore, its global convergence is established under the weak Wolfe line search.
Now, motivated by the ideas of Jian et al. [18], in this paper we suggest a hybrid conjugate gradient method that inherits the strengths of the \(\beta _{k}^{LS},\ \beta _{k}^{HS},\ \beta _{k}^{DY}\) and \(\beta _{k}^{CD}\) methods by introducing \(\beta _{k}^{PKT}\) as
with direction \(d_{k}\) defined as
Now, with \(\beta _{k}\) and \(d_{k}\) defined as in (7) and (8), respectively, we present our hybrid conjugate gradient algorithm below.

Global convergence of the proposed method
The following standard assumptions which have been used extensively in the literature are necessary to analyse the global convergence properties of our hybrid method.
Assumption 3.1
The level set
is bounded, where \(x_{0}\in {\mathbb {R}}^n\) is the initial guess of the iterative method (2).
Assumption 3.2
In some neighbourhood N of X, the objective function f is continuous and differentiable, and its gradient is Lipschitz continuous, that is, there exists a constant \(L>0\) such that
If Assumptions 3.1 and 3.2 hold, then there exists a positive constant \(\varsigma\) such that
Lemma 3.1
Consider the sequence \(\{g_{k}\}\) and \(\{d_{k}\}\) generated by Algorithm 1. Then, the sufficient descent condition
holds.
Proof
If \(k=0\) or \(|g_{k}^{T}g_{k-1}|\ge 0.2 \Vert g_{k}\Vert ^{2},\) then the search direction \(d_{k}\) is given by
This gives
Otherwise, the search direction \(d_{k}\) is given by
Now, if we pre-multiply Eq. (11) by \(g_{k}^T,\) we get
Therefore, the new method satisfies the sufficient descent property (10) for all k. \(\square\)
Lemma 3.2
Suppose that Assumptions 3.1 and3.2 hold. Let the sequence \(\{x_{k}\}\) be generated by (2) and the search direction\(d_{k}\) be a descent direction. If\(\alpha _{k}\) is obtained by the strong Wolfe line search, then the Zoutendijk condition
holds.
Lemma 3.3
For any\(k\ge 1,\) the relation\(0< \beta _{k}^{PKT}\le \beta _{k}^{CD}\) always holds.
Proof
From (5) and (10), it follows that
and since \(0<\sigma <1,\) we have
Also, by descent condition (10), we get
implying
Therefore, from (7), (13) and (14), it is clear that \(\beta _{k}^{PKT}>0.\) Moreover, if \(0<g_{k}^{T}g_{k-1}<\Vert g_{k}\Vert ^{2},\) then
and since \(\max \{d_{k-1}^{T}y_{k-1},-g_{k-1}^{T}d_{k-1}\}\ge -g_{k-1}^{T}d_{k-1},\) we have
Hence, lemma is proved. \(\square\)
Theorem 3.1
Suppose that Assumptions 3.1 and 3.2 hold. Consider the sequences \(\{g_{k}\}\) and \(\{d_{k}\}\) generated by Algorithm 1. Then
Proof
Assume that (15) does not hold. Then there exists a constant \(r>0\) such that
Letting \(\xi _{k}= 1+\beta _{k}^{PKT}\frac{d_{k-1}^{T}g_{k}}{\Vert g_{k}\Vert ^{2}},\) it follows from (8) that
Squaring both sides gives
Now, dividing by \((g_{k}^{T}d_{k})^{2}\) and applying the descent condition \(g_{k}^{T}d_{k}= -\Vert g_{k}\Vert ^{2}\) yields
Since \(\beta _{k}^{PKT}\le \beta _{k}^{CD}=\frac{\Vert g_{k}\Vert ^{2}}{-g_{k-1}^{T}d_{k-1}},\) we obtain
Noting that
and using (17) recursively yields
From (16), we have
Thus,
which implies that
This contradicts the Zoutendjik condition (12), concluding the proof. \(\square\)
Numerical results
In this section, we analyse the numerical efficiency of our proposed \(\beta _k^{PKT}\) method, herein denoted PKT, by comparing its performance to that of Jian et al. [18], herein denoted N, and that of Alhawarat et al. [3], herein denoted AZPRP, on a set of 55 unconstrained test problems selected from [4]. We stop the iterations if either \(\Vert g_{k}\Vert \le 10^{-5}\) or a maximum of 10,000 iterations is reached. All the algorithms are coded in MATLAB R2019a. The authors for both N and AZPRP methods suggested that their algorithms will have optimal performance if they are implemented with the generalized Wolfe line search conditions (6) with the following choice of parameters: \(\sigma =0.1, \ \delta = 0.0001 \ {\text {and}}\ \sigma _{1}=1-2\delta\) for N method and \(\sigma =0.4, \ \delta = 0.0001 \ {\text {and}}\ \sigma _{1}=0.1\) for AZPRP method. Hence for our numerical experiments, we set the parameters of N and AZPRP as determined in the respective papers. For the PKT method, we implemented the strong Wolfe line search conditions with \(\delta = 0.0001 \ {\text {and}}\ \sigma =0.05.\)
Numerical results are presented in Table 1, where “Function” denotes name of test problem, “Dim” denotes dimension of test problem,“NI” denotes number of iterations, “FE” denotes number of function evaluations, “GE” denotes number of gradient evaluations, “CPU” denotes CPU time in seconds and “-” means that the method failed to solve the problem within 10,000 iterations. The bolded figures show the best performer for each problem. From Table 1, we observe that the PKT and AZPRP methods successfully solved all the problems, whereas the N method failed to solve one problem within 10,000 iterations. Moreover, the numerical results in the table indicate that the new PKT method is competitive as it is the best performer for a significant number of problems.
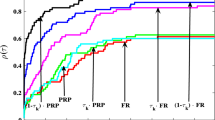
To further illustrate the performance of the three methods, we adopted the performance profile tool proposed by Dolan and Morè [7]. This tool evaluates and compares the performance of \(n_{s}\) solvers running on a set of \(n_{p}\) problems. The comparison between the solvers is based on the performance ratio
where \(f_{p,s}\) denotes either number of functions (gradient) evaluations, number of iterations or CPU time required by solver s to solve problem p. The overall evaluation of the performance of the solvers is then given by the performance profile function
where \(\tau \ge 0.\) If solver s fails to solve a problem p, we set the ratio \(r_{p,s}\) to some sufficiently large number.
The corresponding profiles are plotted in Figs. 1, 2, 3 and 4, where Fig. 1 shows the performance profile of number of iterations, Fig. 2 shows the performance profile of number of gradient evaluations, Fig. 3 shows the performance profile of function evaluations and Fig. 4 shows the performance profile of CPU time. The figures illustrate that the new method outperforms the AZPRP and N conjugate gradient methods.
Conclusion
In this paper, we developed a new hybrid conjugate gradient method that inherits the features of the famous Liu and Storey (LS), Hestenes and Stiefel (HS), Dai and Yuan (DY) and Conjugate Descent (CD) conjugate gradient methods. The global convergence of the proposed method was established under the strong Wolfe line search conditions. We compared the performance of our method with those of Jian et al. [18] and Alhawarat et al. [3] on a number of benchmark unconstrained optimization problems. Evaluation of performance based on the tool of Dolan-Mor\(\acute{e}\) [7] showed that the proposed method is both efficient and effective.
References
Abbo, K.K., Hameed, N.H.: New hybrid conjugate gradient method as a convex combination of Liu-Storey and Dixon methods. J. Multidiscip. Model. Optim. 1(2), 91–99 (2018)
Abdullahi, I., Ahmad, R.: Global convergence analysis of a new hybrid conjugate gradient method for unconstrained optimization problems. Malays. J. Fundam. Appl. Sci. 13(2), 40–48 (2017)
Alhawarat, A., Salleh, Z., Mamat, M., Rivaie, M.: An efficient modified Polak-Ribi\(\grave{e}\)re-Polyak conjugate gradient method with global convergence properties. Optim. Methods Softw. 32(6), 1299–1312 (2017)
Andrei, N.: An unconstrained optimization test functions collection. Adv. Model. Optim. 10(1), 147–161 (2008)
Babaie-Kafaki, S.: A quadratic hybridization of Polak-Ribi\(\grave{e}\)re-Polyak and Fletcher-Reeves conjugate gradient methods. J. Optim. Theory Appl. 154(3), 916–932 (2012)
Dai, Y.H., Yuan, Y.: A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 10(1), 177–182 (1999)
Dolan, E.D., Morè, J.J.: Benchmarking optimization software with performance profiles, Math. Program., 91, 201–214 (2002)
Djordjević, S.S.: New hybrid conjugate gradient method as a convex combination of LS and FR methods. Acta Math. Sci. 39(1), 214–228 (2019)
Faramarzi, P., Amini, K.: A modified spectral conjugate gradient method with global convergence. J. Optim. Theory Appl. 182(2), 667–690 (2019)
Fletcher, R.: Practical Methods of Optimization, Unconstrained Optimization. Wiley, New York (1987)
Fletcher, R., Reeves, C.M.: Function minimization by conjugate gradients. Comput. J. 7(2), 149–154 (1964)
Gu, B., Sun, X., Sheng, V.S.: Structural minimax probability machine. IEEE Trans. Neural Netw. Learn. Syst. 28(7), 1646–1656 (2017)
Hager, W.W., Zhang, H.: A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J. Optim. 16(1), 170–192 (2005)
Hager, W.W., Zhang, H.: The limited memory conjugate gradient method. SIAM J. Optim. 23(4), 2150–2168 (2013)
Hassan, B.A., Alashoor, H.A.: A new hybrid conjugate gradient method with guaranteed descent for unconstraint optimization. Al-Mustansiriyah J. Sci. 28(3), 193–199 (2017)
Hestenes, M.R., Stiefel, E.: Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bureau Stand. 49(6), 409–436 (1952)
Huang, H., Wei, Z., Yao, S.: The proof of the sufficient descent condition of the Wei–Yao–Liu conjugate gradient method under the strong Wolfe–Powell line search. Appl. Math. Comput. 189(2), 1241–1245 (2007)
Jian, J., Han, L., Jiang, X.: A hybrid conjugate gradient method with descent property for unconstrained optimization. Appl. Math. Model. 39, 1281–1290 (2015)
Khakrah, E., Razani, A., Mirzaei, R., Oveisiha, M.: Some metric characterization of well-posedness for hemivariational-like inequalities. J. Nonlinear Funct. Anal. 2017, 44 (2017)
Khakrah, E., Razani, A., Oveisiha, M.: Pascoletti–Serafini scalarization and vector optimization with a vaiable ordering structure. J. Stat. Manag. Syst. 21(6), 917–931 (2018)
Khakrah, E., Razani, A., Oveisiha, M.: Pseudoconvex multiobjective continuous-time problems and vector variational inequalities, Int. J. Ind. Math. 9(3) (2017), Article ID IJIM-00861, 8 pages
Li, J., Li, X., Yang, B., Sun, X.: Segmentation-based image copy-move forgery detection scheme. IEEE Trans. Inf. Forensics Secur. 10, 507–518 (2015)
Li, X., Zhao, X.: A hybrid conjugate gradient method for optimization problems. Nat. Sci. 3, 85–90 (2011)
Liu, J.K., Li, S.J.: New hybrid conjugate gradient method for unconstrained optimization. Appl. Math. Comput. 245, 36–43 (2014)
Li, W., Yang, Y.: A nonmonotone hybrid conjugate gradient method for unconstrained optimization. J. Inequal. Appl. 2015, 124 (2015). https://doi.org/10.1186/s13660-015-0644-1
Liu, Y., Storey, C.: Efficient generalized conjugate gradient algorithms, Part 1: theory. J. Optim. Theory Appl. 69(1), 129–137 (1991)
Mtagulwa, P., Kaelo, P.: An efficient modified PRP-FR hybrid conjugate gradient method for solving unconstrained optimization problems. Appl. Numer. Math. 145, 111–120 (2019)
Polak, E., Ribi\(\acute{e}\)re, G.: Note sur la convergence de directions conjugées, Rev. Francaise Informat Recherche Opèrationelle, 3e Ann\(\acute{e}\)e, 16, 35–43 (1969)
Polyak, B.T.: The conjugate gradient method in extreme problems. USSR Comput. Math. Math. Phys. 9(4), 94–112 (1969)
Salih, Y., Hamoda, M.A., Rivaie, M.: New hybrid conjugate gradient method with global convergence properties for unconstrained optimization. Malays. J. Comput. Appl. Math. 1(1), 29–38 (2018)
Touati-Ahmed, D., Storey, C.: Efficient hybrid conjugate gradient techniques. J. Optim. Theory Appl. 64(2), 379–397 (1990)
Wei, Z., Yao, S., Liu, L.: The convergence properties of some new conjugate gradient methods. Appl. Math. Comput. 183(2), 1341–1350 (2006)
Xu, X., Kong, F.: New hybrid conjugate gradient methods with the generalized Wolfe line search. SpringerPlus 5(1), 881 (2016). https://doi.org/10.1186/s40064-016-2522-9
Yao, S., Wei, Z., Huang, H.: A note about WYL’s conjugate gradient method and its application. Appl. Math. Comput. 191(2), 381–388 (2007)
Yuan, G., Meng, Z., Li, Y.: A modified Hestenes and Stiefel conjugate gradient algorithm for large scale nonsmooth minimizations and nonlinear equations. J. Optim. Theory Appl. 168, 129–152 (2016)
Zhou, Z., Wang, Y., Wu, Q.M.J., Yang, C.N., Sun, X.: Effective and efficient global context verification for image copy detection. IEEE Trans. Inf. Forensics Secur. 12(1), 48–63 (2017)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kaelo, P., Mtagulwa, P. & Thuto, M.V. A globally convergent hybrid conjugate gradient method with strong Wolfe conditions for unconstrained optimization. Math Sci 14, 1–9 (2020). https://doi.org/10.1007/s40096-019-00310-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-019-00310-y