Generalized Tietjen–Moore test to detect outliers

Abstract

An outlier is an observation that appears to deviate from other observations in the sample and outlier detection is one of the most important tasks in data analysis. One of the fundamental assumptions of most parametric multivariate techniques is multivariate normality, which implies the absence of multivariate outliers. The basis for multivariate outlier detection is based on the Mahalanobis distance and outlier detection methods have been suggested for numerous applications in the literature. In this work, Tietjen–Moore test is generalized for multivariate data. A simulation study is carried out to evaluate the performance of the multivariate outlier detection methods under various conditions. The results show that the proposed method gives better results depending on whether or not the data set is multivariate normal.

Introduction

An outlier is an observation that appears to deviate from other observations, namely, inconsistent with the reminder [2, 6]. The detection of outliers in multivariate data is one of the most important problems in the physical, chemical, medical and engineering sciences. The interest in outlier detection procedures has been growing since the researchers are not only interested in the regular data but they also wish to find out the irregular data and consequently the source of the data abnormality. Most of the standard multivariate analysis techniques rely on the assumption of normality and require the use of estimates for both the location and scale parameters of the distribution and most of the statistical techniques are sensitive to the presence of outliers. Outliers may be univariate or multivariate. The most common way of identifying multivariate outliers in a multivariate normal data set is to calculate Mahalanobis distance. Moreover, there are robust and nonrobust procedures to identify outliers in multivariate data. Many methods have been proposed for multivariate outlier detection. Garrett [5] introduced the chi-square plot, which draws the empirical distribution function of the robust Mahalanobis distances against the chi-square distribution. Franklin et al. [4] used Stahel–Donoho estimators to identify the multivariate outliers. Alameddine et al. [1] demonstrated a case study to analyze the effectiveness of the minimum covariance determinant MCD, the minimum volume ellipsoid MVE, and M-estimator. Jackson and Chen [8] compared Mahalanobis distances to minimum volume ellipsoid for identifying outliers for multivariate data. Dang and Serfling [3] introduced nonparametric multivariate outlier identifiers based on multivariate depth functions. Pena and Prieto [9] presented a simple multivariate outlier detection procedure and a robust estimator for the covariance matrix. Reza and Ruhi [10] studied a new method for outlier detection using independent component analysis.

This paper generalizes the Tietjen–Moore test for multivariate data to detect the multivariate outliers. The outline of the paper is as follows. In Sect. 2, the methodology of this paper is given. Firstly, Tietjen–Moore test for univariate outliers is explained in Sect. 2.1. Generalized Tietjen–Moore test for multivariate outliers will be defined in Sect. 2.3. Moreover, robust minimum covariance determinant estimator (MCDE) is given in Sect. 2.2. Simulation study is given in detail in Sect. 3 to assess the proposed tests in case of different conditions. The paper ends with the conclusions in Sect. 4.

Methodology

In this section, Tietjen–Moore test for univariate outliers and robust MCDE will be given for the motivation purpose. Generalized Tietjen–Moore test is proposed using MCDE to detect the multivariate outliers.

Tietjen–Moore test for univariate outliers

The Tietjen–Moore test is used to detect multiple outliers in an univariate data set [13]. This test assumes that the underlying distribution follows an approximately normal distribution. The suspected number of outliers is needed to be specified exactly to apply the test properly. The Tietjen–Moore test is defined for the hypothesis:

• $H_0$: There are no outliers in the data set.

• $H_A$: There are exactly k outliers in the data set.

First, n data points are sorted from the smallest to the largest so that $x_i$ denotes the ith largest data value. Then, the test statistic for the k largest point is

$$\begin{aligned} E_k=\frac{\sum _{i=1}^{n-k}(x_i- {\bar{x_k}} )^2 }{\sum _{i=1}^n(x_i-{\bar{x}})^2}, \end{aligned}$$

(2.1)

where ${\bar{x}}$: sample mean for the full data set, ${\bar{x_k}}$: sample mean with the largest k points removed. Similarly, the test statistic for the k smallest point is

$$\begin{aligned} E_k=\frac{\sum _{i=k+1}^{n}(x_i- {\bar{x_k}} )^2 }{\sum _{i=1}^n(x_i-{\bar{x}})^2 }, \end{aligned}$$

(2.2)

where ${\bar{y_k}}$: sample mean with the smallest k4 points removed. To test statistic for outliers in both tails, the absolute residuals are calculated as $r_i=|x_i-{\bar{x}} |$ where $z_i$ denote the $x_i$ values sorted by their absolute residuals in ascending order. The test statistic can be expressed in terms of z values as

$$\begin{aligned} E_k=\frac{\sum _{i=1}^{n-k}(z_i- \bar{z_k} )^2 }{\sum _{i=1}^n(z_i-\bar{z})^2 }, \end{aligned}$$

(2.3)

with $\bar{z}$ denoting the sample mean for the full data set and $\bar{z_k}$ denoting the sample mean with the largest k points removed. The value of the test statistic is between zero and one. If there are no outliers in the data, the test statistic is close to 1.

Robust minimum covariance determinant estimator

The minimum covariance determinant (MCD) is a robust method in the sense that the estimates are not unduly influenced by outliers in the data, even if there are many outliers. The MCD estimator proposed by Rousseeuw [11] is highly robust and very useful to detect outliers in multivariate data. Due to the MCD’s robustness, multivariate outliers can be detected by their large robust distances. The robust distance is defined like the usual Mahalanobis distance (MD) that is sensitive to the masking effect. In the multivariate location and scatter setting, the data are stored in an $n \times {} p$ data matrix ${\mathbf {X}}= (\mathbf {x}1,\ldots ,{\mathbf {x}}n)^t$ with ${\mathbf {x}}i= (x_{i1}, \ldots , x_{ip})^t$ the ith observation, n stands for the number of objects and p for the number of variables. The Mahalanobis distance $\mathrm{MD}(xi)$ expresses that how far away xi is from the center of the cloud, relative to the size of the cloud. The MD is defined as following:

$$\begin{aligned} \mathrm{MD}({\mathbf {x}})=\sqrt{(\mathbf {x}-{\bar{{\mathbf {x}}}})^tS^{-1}({\mathbf {x}}-\bar{\mathbf {x}})}, \end{aligned}$$

(2.4)

where ${\bar{x}}$ is the sample mean and S the sample covariance matrix. However, instead of the nonrobust sample mean and covariance matrix, the robust distance is based on MCD location estimate and scatter matrix as following:

$$\begin{aligned} \mathrm{RD}({\mathbf {x}})=\sqrt{(\mathbf {x}-{\hat{\varvec{\upmu }}}_\mathrm{MCD})^t\hat{\sum }^{-1}_\mathrm{MCD}({\mathbf {x}}-{\hat{\varvec{\upmu }}}_\mathrm{MCD})}, \end{aligned}$$

(2.5)

where ${\hat{\varvec{\upmu }}}_\mathrm{MCD}$ is the MCD estimate of location given by

$$\begin{aligned} {\hat{\varvec{\upmu }}}_\mathrm{MCD}=\frac{\sum _{i=1}^nW(d_i^2){\mathbf {x}}_i}{\sum _{i=1}^nW(d_i^2)}, \end{aligned}$$

(2.6)

and ${\hat{\mathbf \sum}}_\mathrm{MCD}$ is the MCD estimator of covariance given by

$$\begin{aligned} \hat{\mathbf \sum }_\mathrm{MCD}=c_1\frac{1}{n}\sum _{i=1}^nW(d_i^2)(\mathbf {x}_i-{\hat{\varvec{\upmu }}}_{MCD})(\mathbf {x}_i-{\hat{\varvec{\upmu }}}_{MCD})^t \end{aligned}$$

(2.7)

where $d_i=\sqrt{( {\mathbf {x}}-{\hat{\varvec{\upmu }}} _0)^t\hat{\sum }_0^{-1}( {\mathbf {x}}-{\hat{\varvec{\upmu }}} _0)}$ and W an appropriate function. The constant $c_1$ is a consistency factor [7].

The MCD estimators $({\hat{\mu }}, {\hat{\mathbf \sum}}_\mathrm{MCD})$ of multivariate location and scatter have breakdown value ${\epsilon ^*_n(\hat{\mu })=\epsilon ^*_n({\hat{\mathbf \sum}}_\mathrm{MCD})}\approx \frac{n-h}{2}$. The MCD has its highest possible breakdown value ($\epsilon ^*= 50\%$) when $h = [(n + p + l)/2]$. The MCD estimator has a bounded influence function [7].

FAST-MCD algorithm of Rousseeuw and Van Driessen [12] is mainly used to compute efficiently the MCD estimator. MCDCOV computes the MCD estimator of a multivariate data set. This estimator is given by the subset of h observations with smallest covariance determinant. The MCD location estimator is then the mean of those h points, and the MCD scatter estimator is their covariance matrix. The default value of h is roughly 0.75n (where n is the total number of observations), but the user may choose each value between n/2 and n. Based on the raw estimates, weights are assigned to the observation such that outliers get zero weight. The reweighed MCD estimator is then given by the mean and covariance matrix of the cases with non-zero weight [12].

Generalized Tietjen–Moore Test for multivariate outliers

Numerous methods have been suggested to detect the multivariate outliers. The most popular one is the method based on Mahanalobis distance. The presence of multivariate outliers may lead to biased estimation of the parameters and other drawbacks. The basis of Generalized Tietjen–Moore test is the univariate form of Tietjen–Moore test. Suppose, we have a set of multivariate data and we wish to test the multivariate outliers. To test for outliers in both tails, the absolute residuals are calculated as $r_{ij}=|x_{ij}-{\bar{x}}_j|$, where $z_{ij}$ denote the $x_{ij}$ values sorted by their absolute residuals in ascending order. Tietjen–Moore test is generalized for the multivariate data as below:

$$\begin{aligned} E_k=\frac{\sum _{j=1}^{p}\sum _{i=1}^{n-k/p}(z_{ij}- \bar{z}_{jk} )'(z_{ij}- \bar{z}_{jk} ) }{\sum _{j=1}^p\sum _{i=1}^n(z_{ij}-\bar{z}_j)'(z_{ij}-\bar{z}_j)}, \end{aligned}$$

(2.8)

where $z_{ij}$: ith observation in the jth, $\bar{z}_{jk}$: jth dimension mean with k / p points removed, $\bar{z}_j$: jth dimension mean for the full data.

The generalized Tietjen–Moore test is defined for the below hypothesis:

• $H_0$: There are no outliers in the data set

• $H_A$: There are exactly k outliers in the data set.

The test statistic value is between zero and one. If there are no outliers in the data, the test statistic is close to 1. If there are outliers in the data, the test statistic will be closer to zero. $E_k$ is distributed as Beta-distribution and is not affected from the number of sample sizes. In the next section, the simulation study is given to evaluate the performance of the multivariate outlier detection methods under various conditions.

Simulation study

To evaluate the performance of the proposed test and to compare it with each other, we conduct a simulation study with different schemes. We use two pairs of location-scatter estimators: classical $({\bar{x}}; S)$ and MCD [12] with an approximate $25\%$ breakdown point (denoted RMCD25), which has better efficiency than the one with (maximal) $50\%$ breakdown point.

In the simulation study, we generate multivariate normally distributed data with and without outliers for $p=2,4,6$, the total number of observations is set to $N=n*p=60{,}240$ and the simulation runs M = 1000 times. The simulation scenarios are defined as below:

• Normal $(p=2)$ without outliers, $N= 60{,}240$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0 \ \ 12]$ and $\sum _1=$ diag [10.3].

• Normal $(p=4)$ without outliers, $N= 60, 240$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0\ \ 12\ \ 0\ \ 0]$ and $\sum _1=$ diag $[1\ \ 0.3\ \ 1\ \ 1]$.

• Normal $(p = 6)$ without outliers, $N= 60{,}240$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$ and $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$.

• Normal $(p = 2) , N= 60, 240,$ $90\%$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0\ \ 12]$ and $\sum _1=$ diag $[1\ \ 0.3]$ and plus 10 $(k=6,24)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6]$.

• Normal $(p = 2) , N= 60, 240,$ $80\%$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0\ \ 12]$ and $\sum _1=$ diag $[1\ \ 0.3]$ and plus $20\%$ $(k = 12, 48)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6]$.

• Normal $(p = 4)$, $N= 60, 240$, $90\%$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0\ \ 12\ \ 0\ \ 0]$ and $\sum _1=$ diag $[1\ \ 0.3\ \ 1\ \ 1]$ and plus $10\%$ $(k=6,24)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6\ \ 0\ \ 0]$.

• Normal $(p = 4) , N= 60, 240,$ $80\%$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0\ \ 12\ \ 0\ \ 0]$ and $\sum _1=$ diag $[1\ \ 0.3\ \ 1\ \ 1]$ and plus $20\%$ (k = 12, 48) outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6\ \ 0\ \ 0]$.

• Normal $(p = 6)$, $N= 60, 240$, $90\%$ observations from $N(\mu _1;\sum _1)$,$\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$ and $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$ and plus $10\%$ $(k=6,24)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6\ \ 0\ \ 0\ \ 3\ \ 10]$.

• Normal $(p = 6)$ , $N= 60, 240$, $80\%$ observations from $N(\mu _1;\sum _1)$, $\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$ and $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$ and plus $20\%$ (k=12,48) outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6\ \ 0\ \ 0\ \ 3\ \ 10]$.

In the next step of the simulation study, we generate multivariate non-normally distributed data with and without outliers for $p=2,4,6$ and the total number of observations is set to $N=n*p = 60, 240$. The simulation scenarios are defined as below:

• Non-normal $(p=2)$ without outliers, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 20 for N = 60, 80 for N = 240 observations from $N(\mu _3;\sum _2)$, $\mu _1=[0\ \ 12]$, $\mu _2=[1.5\ \ 6]$, $\mu _3=[0\ \ 0]$, $\sum _1=$ diag $[1\ \ 0.3]$ and $\sum _2=$ diag $[0.2\ \ 9]$.

• Non-normal $(p=4)$ without outliers, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12\ 0 \ 0]$, $\mu _2=[1.5 \ 6 \ 0 \ 0]$, $\mu _3=[0 \ 0 \ 0 \ 0]$, $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1]$.

• Non-normal $(p = 6)$ without outliers, 20 for $N=60, 80$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 20 for $N=60, 80$ for N = 240 observations from $N(\mu _2;\sum _2)$, 20 for $N=60, 80$ for N = 240 observations from$N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$, $\mu _2=[1.5 \ 6 \ 0 \ 0 \ 1 \ 9]$ $\mu _1=[0 \ 0 \ 0 \ 0 \ 0 \ 0]$, $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1 \ 0.8 \ 5]$.

• Non-normal $(p=2)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 18 for N = 60, 72 for N = 240 observations from $N(\mu _2;\sum _2)$, 18 for $N=60, 72$ for N = 240 observations from $N(\mu _3;\sum _2)$, $\mu _1=[0\ \ 12]$, $\mu _2=[1.5\ \ 6]$, $\mu _3=[0\ \ 0]$, $\sum _1=$ diag $[1\ \ 0.3]$ and $\sum _2=$ diag $[0.2\ \ 9]$ and plus $10\%$ $(k=6,24)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6]$.

• Non-normal $(p=4)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _3;\sum _2)$ $\mu _1=[0 \ 12 \ 0 \ 0]$, $\mu _2=[1.5 \ 6 \ 0 \ 0]$, $\mu _3=[0 \ 0 \ 0 \ 0]$, $\sum _1=\mathrm{diag}[1 \ 0.3 \ 1 \ 1]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1]$ and plus $20\%$ (k=6,24) outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2\ \ 6 \ 0 \ 0]$.

• Non-normal $(p=6)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 18 for $N=60, 72$ for $N=240$ observations from $N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$, $\mu _2=[1.5 \ 6 \ 0 \ 0 \ 1 \ 9]$ $\mu _3=[0 \ 0 \ 0 \ 0 \ 0 \ 0]$ $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1 \ 0.8 \ 5]$ and plus $10\%$ $(k=6,24)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2 \ 6 \ 0 \ 0 \ 3 \ 10]$.

• Non-normal $(p=2)$, 16 for $N=60, 64$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 16 for $N=60$, 64 for $N=240$ observations from $N(\mu _2;\sum _2)$, 60 observations from $N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12 ]$, $\mu _2=[1.5 \ 6 ]$, $\mu _3=[0 \ 0 ]$, $\sum _1=\mathrm{diag}[1 \ 0.3 ]$ and $\sum _2=$ diag $[0.2 \ 9 ]$ and plus $20\%$ $(k=12,48)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2 \ 6 ]$.

• Non-normal $(p = 4)$ , 16 for $N=60, 64$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 16 for $N=60, 64$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 60 observations from $N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12 \ 0 \ 0]$, $\mu _2=[1.5 \ 6 \ 0 \ 0]$, $\mu _3=[0 \ 0 \ 0 \ 0]$, $\sum _1=\mathrm{diag}[1 \ 0.3 \ 1 \ 1]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1]$ and plus $10\%$ $(k=12,48)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2 \ 6 \ 0 \ 0]$.

• Non-normal $(p = 6)$, 16 for $N=60, 64$ for $N=240$ observations from $N(\mu _1;\sum _1)$, 16 for $N=60, 64$ for $N=240$ observations from $N(\mu _2;\sum _2)$, 60 observations from $N(\mu _3;\sum _2)$, $\mu _1=[0 \ 12 \ 0 \ 0 \ 3 \ 6]$, $\mu _2=[1.5 \ 6 \ 0 \ 0 \ 1 \ 9]$, $\mu _3=[0 \ 0 \ 0 \ 0 \ 0 \ 0]$, $\sum _1=$ diag $[1 \ 0.3 \ 1 \ 1 \ 0.5 \ 2]$ and $\sum _2=$ diag $[0.2 \ 9 \ 1 \ 1]$ and plus $20\%$ $(k=12,48)$ outlying observations from $N(\mu ;0.01*I)$, $\mu =[-2 \ 6\ \ 0 \ 0 \ 3 \ 10]$.

Fig. 1

Index-robust distance plot for multivariate data N = 60,240 and p = 2

Fig. 2

The robust tolerance ellipse for multivariate data with N = 60, 240 and p = 2

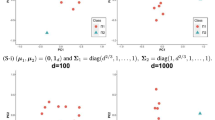
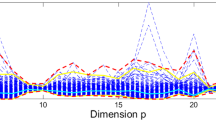
The index-robust distance plots are given in Fig. 1 both for clean and contaminated data. The horizontal line represents the number of observation in one dimension. Figure 1 clearly shows outliers for contaminated data. Figure 2 displays the robust 97.5% tolerance ellipse based on robust distances for multivariate data with N = 60, 240 and p = 2.

Fig. 3

Mahalanobis distances and robust distances for multivariate data p = 2, N = 60, 240

Mahalanobis distances and robust distances for the multivariate data for p = 2, N = 60,240 are illustrated in Fig. 3. This illustrates the masking effect: classical estimates can be highly affected by outlying observations. To get a reliable analysis of multivariate data with outliers, robust estimators are required that can resist possible outliers.

Table 1 The results of Ek for normal multivariate data

Table 2 The results of Ek for non-normal multivariate data

The value of the test statistic lies between zero and one. If there is no outlier in the data, the test statistic is close to 1. If there are outliers in the data, the test statistic will be closer to zero. The robust test statistics give smaller values, thus the test statistics are used in the case of contamination.

In Tables 1 and 2: $E_{k1}$ gives the $E_k$ values obtained from the classic residuals based on classic estimators. $E_{k2}$ gives the $E_k$ values obtained from robust residuals based on MCD estimators. $E_{k3}$ gives the $E_k$ values obtained from weighted residuals based on the MCD estimators.

The results for normal and non-normal multivariate data in Tables 1 and 2 are similar and can be summarized as follows:

• For clean sample data, test statistic $E_{k1}$ based on classic estimators is close to 1. So the null-hypothesis (there are no outliers) is not rejected, as expected. The values of the robust weighted test statistic $E_{k3}$ is also close to 1 under normal distribution. So it can be used as an alternative to $E_{k1}$. Under the non-normal distribution, the robust test $E_{k2}$ also can be used for large sample size.

• Under the contamination, the test statistic must reject the null-hypothesis. If there are outliers in the data, the test statistic is close to 0. Under the 10 and $20\%$ contamination, $E_{k3}$’s performance is better than $E_{k2}$. These two robust test statistics show up the outliers and so can be used to detect outliers.

• When the contamination amount and sample size decrease, $E_{k2}$ gives better results.

• In the case of contamination, the $E_k$ test statistic based on classic estimators is deteriorated.

• The weighted robust test statistic has the best performance.

• The robust test statistic is not affected by the number of sample sizes.

The MCD estimator is a highly robust estimator of multivariate location and scale. Therefore, detection of multivariate outlier using MCD estimator could be a good solution. Results are valid for both normal and non-normal multivariate cases to detect outliers. The results show that the proposed method give better results depending on whether or not the data set is multivariate normal.

From the simulation study, we can conclude that the proposed method is applicable for the multivariate outlier.

Conclusions

Univariate or multivariate outliers are important because they change the results of data analysis. Even though the easiest way to detect the multivariate outliers is multidimensional scatter plot, some methods based on the Mahalanobis distance or Cooks distance have been suggested in the literature. These distances use estimates of the location and scatter to identify values that are considerably far away from the bulk of data. The principal component might be a good alternative method but its drawback is that it may fail when the distribution has multi-modal. In this paper, we generalize the Tietjen–Moore test for multivariate data. In the formulation, the robust estimators of the mean and the covariance matrix are replaced by the classical estimators to avoid the masking effect. The value of the test statistic always lies between zero and one. A simulation study is conducted to evaluate the performance of the multivariate outlier detection methods under various conditions. The results reveal that the proposed method gives better results depending on whether or not the data set is multivariate normal even though multivariate analyses require checking the multivariate normality.