Abstract
An effective technique based on fractional calculus in the sense of Riemann–Liouville has been developed for solving weakly singular Volterra integral equations of the first and second kinds. For this purpose, orthogonal Chebyshev polynomials are applied. Properties and some operational matrices of these polynomials are first presented and then the unknown functions of the integral equations are represented by these polynomials in the matrix form. These matrices are then used to reduce the singular integral equations to some linear algebraic system. For solving the obtained system, Galerkin method is utilized via Chebyshev polynomials as weighting functions. The method is computationally attractive, and the validity and accuracy of the presented method are demonstrated through illustrative examples. As shown in the numerical results, operational matrices, even for first kind integral equations, have relatively low condition numbers, and thus, the corresponding matrices are well posed. In addition, it is noteworthy that when the solution of equation is in power series form, the method evaluates the exact solution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The aim of this study is to present a high-order computational method for solving special cases of singular Volterra integral equations of the first and second kinds, namely Abel’s integral equations, defined by
and
where \(f(x)\in C[0,T]\) is the known function and y(x) is the unknown function that to be determined, and T is a positive constant.
Abel’s equation is one of the integral equations derived directly from a concrete problem of mechanics or physics (without passing through a differential equation). Historically, Abel’s problem is the first one that led to the study of integral equations. The generalized Abel’s integral equations on a finite segment appeared in the paper of Zeilon [15] for the first time.
A comprehensive reference on Abel-type equations, including an extensive list of applications, can be found in [8, 9].
The construction of high-order methods for the equations is, however, not an easy task because of the singularity in the weakly singular kernel. In fact, in this case, the solution y is generally not differentiable at the endpoints of the interval [3], and due to this, to the best of the authors’ knowledge, the best convergence rate ever achieved remains only at polynomial order. For example, if we set uniform meshes with \(n+1\) grid points and apply the spline method of order m, then the convergence rate is only \(O(n^{-2P})\) at most (see [4, 12]), and it cannot be improved by increasing m. One way of remedying this is to introduce graded meshes [13]. By doing so, the rate is improved to \(O(n^{-m})\), which now depends on m, but still at polynomial order. Rashit Ishik [10] used Bernstein series solution for solving linear integro-differential equations with weakly singular kernels. In [5] and [6], wavelets method was applied for solution of nonlinear fractional integro-differential equations in a large interval and systems of nonlinear singular fractional Volterra integro-differential equations. Authors of [11] applied fractional calculus for solving Abel integral equations. The expansions approach for solving cauchy integral equation of the first kind is discussed in [14].
In this paper, we use the Chebyshev polynomials operational matrices via Galerkin method for solving weakly singular integral equations. Our method consists of reducing the given weakly singular integral equation to a set of algebraic system by expanding the unknown function by Chebyshev polynomials of the first kind. Galerkin method is utilized to solve the obtained system.
The structure of this paper is arranged as follows. The main problem and brief history of some presented methods are expressed in Sect. 1. In Sect. 2, we present some necessary definitions and mathematical preliminaries of the fractional calculus theory in the sense of Riemann–Liouville. Section 3 is devoted to introducing Chebyshev polynomials, properties and some operational matrices of these functions. In Sect. 4, Chebyshev polynomials are applied as testing and weighting functions of Galerkin method for efficient solution of Eq. 1. In Sect. 5, we report our numerical founds and compare with other methods in solving these integral equations, and Sect. 6 contains our conclusion.
Some preliminaries in fractional calculus
In this section, we briefly present some definitions and results in fractional calculus for our subsequent discussion. The fractional calculus is the name for the theory of integrals and derivatives of arbitrary order, which unifies and generalizes the notions of integer-order differentiation and n-fold integration [7]. There are various definitions of fractional integration and differentiation, such as Grunwald–Letnikov, and Caputo and Riemann–Liouville’s definitions. In this study, fractional calculus in the sense of Riemann–Liouville is considered.
Definition 1
Let f be a real function on [a, b] and \(0<\alpha <1\). Then, the left and right Riemann–Liouville fractional integral operators of order \(\alpha\) for the function f are defined, respectively, as
Definition 2
For \(f\in C[a,b]\), the left and right Riemann–Liouville fractional derivatives are defined, respectively, as
In this study, the left Riemann–Liouville fractional integral operator is utilized to transform singular integral equation to some algebraic system. Therefore, for abbreviation, the mentioned operator is denoted by \(I^{\alpha }\).
Theorem 1
The operator \(I^{\alpha }\) (stand for left and right Riemann–Liouville fractional integral operator) satisfies the following properties:
Proof
We prove the proposition for left Riemann–Liouville fractional integral operator and the proof for right Riemann–Liouville fractional integral operator can be done similarly. For the part (1), we have
In addition, for part (2), we have
by changing the variable \(t=rx\), we get
now, using the formulae of the beta function, we have
On the other hand, we know that the beta function can be written in terms of the Gamma function as follows:
so we have
\(\square\)
Chebyshev polynomials
In this section, a brief summary of orthogonal Chebyshev polynomials is expressed.
Definition 3
The nth degree of Chebyshev polynomials is defined by
where \(t=\cos (\theta )\). The roots of Chebyshev polynomial of degree \(n+1\) can be obtained by
In addition, the following successive relation holds for Chebyshev polynomials:
where
Chebyshev polynomials are orthogonal with respect to the weight function \(w(x)=\frac{1}{\sqrt{1-x^{2}}}\) in the interval \([-1,1]\), that is
Matrix form
We can represent Chebyshev polynomials in the matrix form. Put
then we can write
where T is a \((n+1)\times (n+1)\) matrix defined by
and the first element of each row is \(t_{i0}=\cos (\frac{i \pi }{2})\), \(i=0,\ldots ,n\). In addition, other elements are defined by \(t_{i,j}=sign (t_{i-1,j-1})(2\vert t_{i-1,j-1}\vert +\vert t_{i-2,j}\vert .\) The Chebyshev polynomials are defined in the \([-1,1]\), but the integration interval of Eqs. (1) and (2) is [0, T]. To transform the interval \([-1,1]\) to [0, T], we apply the \((n+1)\times (n+1)\) shift matrix R, which is defined by
and \(\gamma _{1}=-1,\gamma _{2}=\frac{2}{T}.\) Thus, the shifted Chebyshev polynomial matrix is written as WX, where \(W=T R\).
Function approximation
A function \(y(x) \in L_{2}[0,T]\), can be expressed in terms of the shifted Chebyshev polynomials as [2]
where \(\varphi _{j}\) is the shifted Chebyshev polynomial of degree j. The coefficients \(c_{j}\) are given by
and
Operational matrix of fractional Integration
The fractional integral of Chebyshev polynomials can be defined by
where
and \(*\) is point by point product and A is \((n+1)\times (n+1)\) lower triangular matrix defined by
In addition, for each function g(x), approximated by shifted Chebyshev functions (\(g(x)=D^{T}WX\)), the fractional integral can be written as
Numerical implementation
In this section, the shifted Chebyshev polynomials are applied for solving singular integral Eqs. (1) and (2). For this purpose, initially, the singular integral equation is transformed to nonsingular integral equation, utilizing Riemann–Liouville calculus.
Putting \(-\alpha =\beta -1\) in the integral part of the Eqs. (1) and (2), we get
by definition of Riemann–Liouville fractional integral operator, the current relation can be rewritten as
Now, the unknown function y(x) is approximated by shifted Chebyshev polynomials as
where \(C^{T}\) is the unknown vector, that to be determined. In the following, we describe the method in detail for the first and second kinds.
The first kind
Consider the weakly singular Volterra integral equation of the first kind (1), according to Eq. (10), we have
substituting Eqs. (11) and (8) in (12), we can get
Therefore, singular integral equation (1) is transformed to the above algebraic system. For solving this system, Galerkin procedure is utilized via shifted Chebyshev polynomials. Put \(\Gamma (\beta ) (A*W)=\Lambda\) and suppose \(\varphi _{i}(x)\) be the shifted Chebyshev polynomial of degree i, which can be written as
where \(W_{i}\) is the ith row of the matrix W. Multiplying Eq. (13) by \(\varphi _{i}(x)\), we get
Putting
and
we get
by integrating current equations from 0 to T, we have
where \(P_{x}\) and \(P^{\beta }\) are related integration operational matrix, defined by
Considering Eq. (17) for \(i=0,\ldots ,n\), we get
a system of \(n+1\) equations and \(n+1\) unknowns that can be solved easily.
The second kind
Similarly, for the second kind singular integral equation (2), we have
so Eq. (19) can be written as
Multiplying Eq. (20) by \(\varphi _{i}(x)\) and integrating from 0 to T, we can rewrite the current equation in the following form:
where
Eq. (21) is a system of \(n+1\) equations and \(n+1\) unknowns that can be solved easily.
Illustrative examples
In this section, for showing the accuracy and efficiency of the described method, we present some examples. Moreover, the condition number of the operational matrices, defined by
are given in corresponding tables. In Examples 1 and 2 singular Volterra integral equation of the second kind, and in examples 3 and 4, singular Volterra integral equation of the first kind is solved. As we know, numerically solving the first kind integral equations is so difficult, because their operational matrices have large condition numbers and in the other words are bad-conditioned, while, as seen in Tables 2 and 3, the maximum condition number of the problem is 64. The abbreviation c.n.m in the tables denotes the condition number of the operational matrices.
Example 1
Consider the following singular integral equation of the second kind:
with the exact solution \(y(x)=x^2\). The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\).
The function y(x) is a polynomial of degree 2 and the least approximation level for Chebyshev polynomials, in this study, is \(N=4\). Therefore, the approximated solution through the presented method is the same as the exact solution, that is \(y_{4}(x)=x^{2}\).
Example 2
Consider the following singular integral equation:
with the exact solution \(y(x)=x^{\frac{3}{2}}\). The solution for y(x) is obtained by the method in Sect. 4 for \(N=4, 8\) and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\):
and the approximate solution for \(N=4\) is calculated as
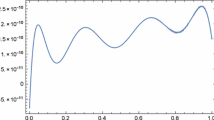
In Table 1, we have presented exact and approximated solutions of Example 2 in some arbitrary points. In addition, the last line of Table 1 shows the condition number of operational matrices. The errors of approximate solutions in the levels \(N=4, 8\), and 12 are shown in Fig. 1.
Graph of estimated solution of Example 2 for \(N=4,8\) and 12
Example 3
Consider the following singular integral equation of the first kind:
with the exact solution \(y(x)=\frac{7\Gamma (1/6)}{18\Gamma (2/3)}\sqrt{\frac{x}{\pi }}\). The solution for y(x) is obtained by the method in Sect. 4 for \(N=4, 8\), and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\):
and the approximate solution for \(N=4\) is calculated as
In Table 2, we present exact and approximate solutions of Example 3 in some arbitrary points and compare them by the results of [1] for \(n=20\). In addition, the last line of Table 2 shows the condition number of operational matrices. Figure 2 illustrates the error of approximate solutions in the levels \(N=4, 8\), and 12.
Example 4
Consider the following singular integral equation of the first kind:
with the exact solution \(y(x)=\frac{3\sqrt{3}}{4}x^{2/3}\). The solution for y(x) is obtained through the method in Sect. 4 for \(N=4, 8\), and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\).
and the approximate solution for \(N=4\) is calculated as
In Table 3, exact and approximated solutions of Example 4 in some arbitrary points are given. The condition number of operational matrices for \(N=4, 8\), and 12 are calculated by Eq. 22, and is shown in the last row of Table 3. Figure 3 is helpful in geometric understanding the errors of approximated solutions in the levels \(N=4, 8\), and 12.
Graph of estimated solution of Example 4 for \(N=4,8\) and 12
Conclusions
In this study, a numerical approach based on Chebyshev polynomials operational matrices was developed to approximate the solution of the weakly singular Volterra integral equations of the first and second kinds. Applying fractional derivative of these polynomials, we have transformed the singular integral equations to some linear algebraic system. The numerical results obtained support the validity and efficiency of the proposed method. It is noteworthy that when the solution of equation is in power series form, the method evaluates the exact solution, such as Example 1. In addition, as can be seen, the operational matrices of first kind integral equations have relatively low condition numbers. Thus, the corresponding matrices are well posed.
References
Avazzadeh, Z., Shafiee, B., Loghmani, G.: Fractional calculus for solving Abel’s integral equations using Chebyshev polynomials. Appl. Math. Sci. 5(45), 2207–2216 (2011)
Doha, E.H., Bhrawy, A.H., Ezz-Eldien, S.S.: Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 35, 5662–5672 (2011)
Graham, I.G.: Singularity expansions for the solutions of second kind Fredholm integral equations with weakly singular convolution kernels. J. Integr. Equ. 4, 1–30 (1982)
Graham, I.G.: Galerkin methods for second kind integral equations with singularities. Math. Comput. 39, 519–533 (1982)
Heydari, M.H., Hooshmandasl, M.R., Maalek Ghaini, F.M., Li, M.: Chebyshev wavelets method for solution of nonlinear fractional integro-differential equations in a large interval. Adv. Math. Phys., Article ID 482083 (2013)
Heydari, M.H., Hooshmandasl, M.R., Mohammadi, F., Cattani, C.: Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 19(1), 37–48 (2014)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and applications of fractional differential equations. North-Holland Mathematics Studies, vol. 204. Elsevier (2006)
Nieto, J.J., Okrasinski, W.: Existence, uniqueness, and approximation of solutions to some nonlinear diffusion problems. J. Math. Anal. Appl. 210(1), 231–240 (1997)
Okrasinski, W., Vila, S.: Determination of the interface position for some nonlinear diffusion problems. Appl. Math. Lett. 11(4), 85–89 (1998)
Rasit Isik, O., Sezer, M., Guney, Z.: Bernstein series solution of a class of linear integro-differential equations with weakly singular kernel. Appl. Math. Comput. 217(16), 7009–7020 (2011)
Saleh, M.H., Amer, S.M., Mohamed, DSh, Mahdy, A.E.: Fractional calculus for solving generalized Abels integral equations using Chebyshev polynomials. Int. J. Comput. Appl. 100(8), 19–23 (2014)
Schneider, C.: Product integration for weakly singular integral equations. Math. Comput. 36, 207–213 (1981)
Vainikko, G., Uba, P.: A piecewise polynomial approximation to the solution of an integral equation with weakly singular kernel. J. Austral. Math. Soc. Ser. B. 22, 431–438 (1981)
Yaghobifar, M., Nik Long, N.M.A., Eshkuvatov, Z.K.: The expansions approach for solving cauchy integral equation of the first kind. Applied Mathematical Sciences. 4(52), 2581–2586 (2010)
Zeilon, N.: Sur quelques points de la theorie de l’equation integrale d’Abel [On some points of the theory of integral equation of Abel type]. Arkiv. Mat. Astr. Fysik. 18, 1–19 (1924)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sahlan, M.N., Feyzollahzadeh, H. Operational matrices of Chebyshev polynomials for solving singular Volterra integral equations. Math Sci 11, 165–171 (2017). https://doi.org/10.1007/s40096-017-0222-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-017-0222-4
Keywords
- Chebyshev polynomials
- Singular integral equations
- Operational matrix
- Fractional calculus
- Galerkin method