Introduction

Many problems in engineering and mechanics appear to be two-dimensional integral equations. For example, it is usually necessary to solve Fredholm integral equations in the calculation of plasma physics [1]. Mckee et al. [2] revealed that a class of nonlinear telegraph equations is equivalent to two-dimensional Volterra integral equations. Graham [3] showed that two-dimensional Ferdholm integral equation used in solving the problems of electrical engineering. Some other applications of two-dimensional integral equations can be found in [2, 4].

In this paper, we consider the nonlinear two-dimensional Volterra integral equation of the second kinds as follows:

$$\begin{aligned} u(x,t)=f(x,t)+Fu(x,t)\quad (x,t) \in D=[a,b]\times [c,d] \end{aligned}$$
(1)

where

$$\begin{aligned} Fu(x,t)=\lambda \int _c^t \int _a^x K(x,t,y,z)N(u(y,z))\mathrm{d}y\mathrm{d}z. \end{aligned}$$

Here, u(x, t) is unknown function and \(u(x,t), f(x,t) \in W_2^{(1,1)}(D), N(.)\) the continues terms in \(W_2^{(1,1)}(D)\), \(W_2^{(1,1)}(D)\) is a reproducing kernel space. Little numerical methods for nonlinear integral equations are written. In this context, the methods used are the block-by-block method [5], block-pulse functions [6], and rationalized Harr function [7].

In this article, we obtain presentation of exact solution nonlinear two-dimensional Volterra integral equation of the second kind in reproducing kernel space, and then, approximate solution is obtained by cutting series. Of course, coefficients of the series on presentation of exact solution obtained with a numerical calculation. The error of the approximate solution is monotone deceasing in the sense of \(\Vert .\Vert _{W_2^{(1,1)}}\).

The fundamental principles of the method

Below are some definitions and theorems that we used in the next sections.

Definition 2.1

[9] The function space \(W_2^1[a,b]\) is defined as follows:

$$\begin{aligned} W_2^1[a,b]=\{f(x)|f(x) \text{ is absolutely continuous,}\,\, f'(x)\in L^2[a,b], x\in [a,b]\}. \end{aligned}$$

Definition 2.2

[9] The inner product and norm in the function space \(W_2^1[a,b]\) are defined as follows:

For any functions \(f(x), g(x) \in W_2^1 [a,b],\)

$$\begin{aligned} \langle f,g \rangle _{W_2^1}=f(a)g(a)+\int _a^b f(x)g(x)\mathrm{d}x \end{aligned}$$

and

$$\begin{aligned} \Vert f\Vert _{W_2^1}=\sqrt{\langle f,f \rangle _{W_2^1}}. \end{aligned}$$

It is easy to prove that \(W_2^1[a,b]\) is an inner space. At [9] prove that function space \(W_2^1[a,b]\) is a Hilbert space and also it is a reproducing kernel space.

Suppose \(R_y(x)\) is the reproducing kernel of \(W_2^1[a,b]\); in this case, we have for any \(f(x)\in W_2^1[a,b]\):

$$\begin{aligned} \langle f(x),R_y(x) \rangle _{W_2^1}=f(y). \end{aligned}$$

With calculation, we obtain that

$$\begin{aligned} R_y(x)=\left\{ \begin{array}{rll} 1-a+x &{}\quad \text{ if } &{} x\le y \\ 1-a+y &{}\quad \text{ if } &{} x>y \end{array} \right. \end{aligned}$$

Let set \(D=[a,b]\times [c,d] \subset \mathcal R^2\).

Definition 2.3

[9] The binary function space is defined as

$$\begin{aligned} W_2^{(1,1)}(D)=\left\{ f(x,y)|f(x,y)\,\, {\rm is} \,\,{\rm completely}\,\, {\rm continuous}\,\,{\rm in}\,\,D,\frac{\partial ^2 f(x,y)}{\partial x \partial y}\in L^2(D)\right\} . \end{aligned}$$

Definition 2.4

[9] The inner product and norm in \(W_2^{(1,1)}(D)\) is defined as follows:

$$\begin{aligned} \langle f(x,y),g(x,y) \rangle _{W_2^{(1,1)}} = \int _c^d \frac{\partial f(a,y)}{\partial y} \frac{\partial g(a,y)}{\partial y}\mathrm{d}y + \langle f(x,c),g(x,c) \rangle _{W_2^1} \end{aligned}$$
$$\begin{aligned} + \int \int _{D} \frac{\partial ^2 f(x,y)}{\partial x \partial y}\frac{\partial ^2 g(x,y)}{\partial x \partial y}\mathrm{d}x\mathrm{d}y \end{aligned}$$

and

$$\begin{aligned} \Vert f\Vert _{W_2^{(1,1)}}=\sqrt{\langle f(x,y),f(x,y) \rangle _{W_2^{(1,1)}}}. \end{aligned}$$

It is easy to prove that \(W_2^{(1,1)}(D)\) is an inner space. At [9] prove that function space \(W_2^{(1,1)}(D)\) is a Hilbert space and also it is a reproducing kernel space which has reproduced kernel:

$$\begin{aligned} K_{(\xi ,\eta )}(x,y)=R_\xi (x)Q_\eta (y) \end{aligned}$$

where \(R_\xi (x),Q_\eta (y)\) are the reproducing kernels of \(W_2^1[a,b]\) and \(W_2^1[c,d]\), respectively.

Therefore, for each \(f(x,y) \in W_2^{(1,1)}(D)\)

$$\begin{aligned} \langle f(x,y),K_{(\xi ,\eta )}(x,y) \rangle =f(\xi ,\eta ). \end{aligned}$$

Thus, if \(K_{(y,z)}(x,t)\) is reproducing kernel of \(W_2^{(1,1)}(D)\), then \(K_{(y,z)}(x,t)=R_y(x)Q_z(t)\), where \(R_y(x)\) and \(Q_z(t)\) are reproducing kernels in \(W_2^1[a,b]\) and \(W_2^1[c,d]\), respectively.

We will display the solution of Eq. (1) in reproducing kernel space \(W_2^{(1,1)}(D)\) for this purpose let \(\phi _i(x,t)=K_{(x_i,t_i)}(x,t)\), where \(\{(x_i,t_i)\}_{i=1}^{\infty }\) is dense in region D. From the property of the reproducing kernel, we have

$$\begin{aligned} \langle u(x,t), \phi _i(x,t) \rangle _{W_2^{(1,1)}(D)}=\langle u(x,t), K_{(x_i,t_i)}(x,t) \rangle _{W_2^{(1,1)}(D)} \end{aligned}$$
$$\begin{aligned} =u(x_i,t_i). \end{aligned}$$

Theorem 2.1

If \(\{(x_i,t_i)\}_{i=1}^\infty\) is dense in the region D, then \(\{\phi _i(x,t)\}_{i=1}^\infty\) is the complete function system of \(W_2^{(1,1)}(D)\).

Proof

Suppose \(u(x,t) \in W_2^{(1,1)}(D)\) if

$$\begin{aligned} \langle u(x,t),\phi _i(x,t) \rangle _{W_2^{(1,1)}(D)}=u(x_i,t_i)=0\quad (i=1,2,\ldots ). \end{aligned}$$

Then, we have \(u(x,t)=0\) from the density of \(\{(x_i,t_i)\}_{i=1}^ \infty\) and continuity of u(x, t).\(\diamond\)

By applying Gram–Schmidt orthonormalization process for \(\{\phi _i(x,t)\}_{i=1}^\infty\)

$$\begin{aligned} \bar{\phi }_i(x,t)=\sum _{k=1}^i\alpha _{ik}\phi _k(x,t) \end{aligned}$$

where \(\alpha _{ik}\) are coefficients of Gram–Schmidt orthonormalization and \(\{\bar{\phi }_i(x,t)\}_{i=1}^\infty\) is a normal orthogonal basis of \(W_2^{(1,1)}(D)\) [9].

Now, the following theorem is obtained.

Theorem 2.2

We assume \(\{(x_i,t_i)\}_{i=1}^\infty\) be dense in region D. If Eq. (1) has a unique solution, then it is as follows:

$$\begin{aligned} u(x,t)=\sum _{i=1}^\infty \sum _{k=1}^i\alpha _{ik}(f(x_k,t_k)+Fu(x_k,t_k))\bar{\phi }_i(x,t). \end{aligned}$$
(2)

Proof

Suppose u(x, t) is the solution of Eq. (1). From Theorem 2.1 and since \(\{\bar{\phi }_i(x,t)\}_{i=1}^\infty\) is a normal orthogonal basis of \(W_2^{(1,1)}(D)\), therefore, we can write

$$\begin{aligned} u(x,t)=\sum _{i=1}^\infty \langle u(x,t),\bar{\phi }_i(x,t) \rangle _{W_2^{(1,1)}}\bar{\phi }_i(x,t) \end{aligned}$$
$$\begin{aligned} =\sum _{i=1}^\infty \sum _{k=1}^i\alpha _{ik} \langle u(x,t),\phi _k(x,t) \rangle _{W_2^{(1,1)}}\bar{\phi }_i(x,t) \end{aligned}$$
$$\begin{aligned} =\sum _{i=1}^\infty \sum _{k=1}^i\alpha _{ik} \langle f(x,t)+Fu(x,t),\phi _k(x,t) \rangle _{W_2^{(1,1)}}\bar{\phi }_i(x,t) \end{aligned}$$
$$\begin{aligned} =\sum _{i=1}^\infty \sum _{k=1}^i\alpha _{ik}(f(x_k,t_k)+Fu(x_k,t_k))\bar{\phi }_i(x,t). \end{aligned}$$

The proof is complete [9].\(\diamond\)

Implementations of the method

In this section, a method will be presented to calculate the solution (2) of the Eq. (1). To this end rewrite (2) as

$$\begin{aligned} u(x,t)=\sum _{i=1}^\infty A_i\bar{\phi }_i(x,t) \end{aligned}$$

where

$$\begin{aligned} A_i =\sum _{k=1}^i \alpha _{ik}(f(x_k,t_k)+Fu(x_k,t_k)) \end{aligned}$$

\(A_i\) is unknown, because u(x, t) is an unknown function. \(A_i\) with a numerical calculation can be approximated by known \(B_i\). For this purpose, put initial function \(u_1(x,t)=f(x,t)\) and n-term approximation for u(x, t) is defined as follows:

$$\begin{aligned} u_{n+1}(x,t)=\sum _{i=1}^n B_i\bar{\phi }_i(x,t) \end{aligned}$$
(3)

where

$$\begin{aligned} B_1=\alpha _{11}(f(x_1,t_1)+Fu_1(x_1,t_1)) \end{aligned}$$
$$\begin{aligned} u_2(x,t)=B_1\bar{\phi }_1(x,t) \end{aligned}$$
$$\begin{aligned} B_2=\sum _{k=1}^2\alpha _{nk}(f(x_k,t_k)+Fu_2(x_k,t_k)) \end{aligned}$$
$$\begin{aligned} u_3(x,t)=B_1\bar{\phi }_1(x,t)+B_2\bar{\phi }_2(x,t) \end{aligned}$$
$$\begin{aligned} \ldots \end{aligned}$$
$$\begin{aligned} B_n=\sum _{k=1}^n \alpha _{nk}(f(x_k,t_k)+Fu(x_k,t_k)) \end{aligned}$$
(4)
$$\begin{aligned} u_{n+1}(x,t)=\sum _{k=1}^n B_k\, \bar{\phi }_k(x,t). \end{aligned}$$

Lemma 3.1

If \((n \rightarrow \infty )\) and \((x_n,t_n) \rightarrow (y,z)\), then \(u_n(x_n,t_n) \rightarrow \bar{u}(y,z) (n \rightarrow \infty )\)

Proof

We have

$$\begin{aligned} \mid u_n(x_n,t_n)-\bar{u}(y,z) \mid =\mid u_n(x_n,t_n)-u_n(y,z)+u_n(y,z)-\bar{u}(y,z) \mid \end{aligned}$$
$$\begin{aligned} \le \mid u_n(x_n,t_n)-u_n(y,z) \mid +\mid u_n(y,z) - \bar{u}(y,z) \mid. \end{aligned}$$

For absolute first on the right side of the above inequality, we have

$$\begin{aligned} \mid u_n(x_n,t_n)-u_n(y,z) \mid = \mid \langle u_n(x,t), K_{(x_n,t_n)}(x,t) - K_{(y,z)}(x,t)\rangle _{W_2^{(1,1)}} \mid \end{aligned}$$
$$\begin{aligned} \le \Vert u_n(x,t)\Vert _{W_2^{(1,1)}} \Vert K_{(x_n,t_n)}(x,t)-K_{(y,z)}(x,t)\Vert _{W_2^{(1,1)}}. \end{aligned}$$

From the convergence of sequence \(\{u_n(x,t)\}_{n=1}^\infty\), we conclude that there exists a constant N, such that

$$\begin{aligned} \Vert u_n(x,t) \Vert _{W_2^{(1,1)}} \le N \Vert \bar{u}(x,t) \Vert _{W_2^{(1,1)}} \end{aligned}$$

when \(n \ge N\). At the same time, it can be proved that

$$\begin{aligned} \Vert K_{(x_n,t_n)}(x,t)-K_{(y,z)}(x,t) \Vert _{W_2^{(1,1)}} \rightarrow 0 \end{aligned}$$

when \(n \rightarrow \infty\). Thus, \(\mid u_n(x_n,t_n) - u_n(y,z) \mid \rightarrow 0\) when \((x_n,t_n) \rightarrow (y,z)\). From \(\Vert u\Vert _c \le M \Vert u\Vert _{W_2^{(1,1)}}\) for any \((y,z) \in D\), it holds that

$$\begin{aligned} \Vert u_n(y,z) - \bar{u}(y,z)\Vert _c \rightarrow 0\;\; (n\rightarrow \infty ) \end{aligned}$$

when

$$\begin{aligned} \Vert u_n(y,z) - \bar{u}(y,z) \Vert _{W_2^{(1,1)}} \rightarrow 0\;\; (n \rightarrow \infty ). \end{aligned}$$

Therefore, here, we conclude that

$$\begin{aligned} u_n(x_n,t_n) \rightarrow \bar{u}(y,z)\;\; (n \rightarrow \infty ) \end{aligned}$$

when \((x_n,t_n) \rightarrow (y,z)\) [9].\(\diamond\).

Using the continuation of N(.), it will be obtained that \(N(u_n(x_n,t_n)) \rightarrow N(\bar{u}(y,z))\) when \(n\rightarrow \infty\). In addition, this shows that

$$\begin{aligned} Fu_n(x_n,t_n) \rightarrow F \bar{u}(y,z) \; (n \rightarrow \infty ). \end{aligned}$$

From the method listed above, convergence theorem will be obtained.

Theorem 3.1

Suppose that the sequence \(\{\Vert u_n(x,t) \Vert _{W_2^{(1,1)}}\}_{n=1}^\infty\) is bounded in (3), if \(\{ (x_i,t_i) \}_{i=1}^ \infty\) is dense in D, then n-term approximate solution \(u_n(x,t)\) converges to the exact solution u(x, t) of Eq. (1) and exact solution is expressed as

$$\begin{aligned} u(x,t)= \sum _{i=1}^ \infty B_i \bar{\phi }_i(x,t) \end{aligned}$$
(5)

where \(B_i\) is given by (4).

Proof

The theorem is proved in three steps:

(a) At this step, we provide that the sequence \(\{u_n(x,t)\}_{n=1}^\infty\) with formula (3) is converged. For this purpose from (4), we have

$$\begin{aligned} u_{n+1}(x,t)=u_n(x,t)+B_n\bar{\phi }_n(x,t). \end{aligned}$$

From recent equality and using the orthogonality of \(\{ \bar{\phi }_i(x,t) \}_{i=1}^ \infty\), it follows

$$\begin{aligned} \Vert u_{n+1}(x,t) \Vert _{W_2^{(1,1)}}^2=\Vert u_n(x,t)\Vert _{W_2^{(1,1)}}^2 + B_n^2. \end{aligned}$$

Thus, sequence \(\{\Vert u_n(x,t)\Vert _{W_2^{(1,1)}}\}_{n=1}^\infty\) is monotone increasing. In other hand, sequence \(\{\Vert u_n(x,t)\Vert _{W_2^{(1,1)}}\}_{n=1}^\infty\) is bounded; therefore, this sequence is convergent. Therefore, there exists a constant c, such that

$$\begin{aligned} \sum _{i=1}^ \infty B_i^2=c. \end{aligned}$$

This illustrate that

$$\begin{aligned} B_i=\sum _{k=1}^i \alpha _{ik}(f(x_k,t_k)+Fu_i(x_k,t_k))\in \ell ^2\quad (i=1,2,\ldots ). \end{aligned}$$

Using the orthogonality of \(\{u_{n+1}(x,t)-u_n(x,t)\}_{n=1}^\infty\) if \(m > n\), then

$$\begin{aligned} \Vert u_m(x,t)-u_n(x,t)\Vert _{W_2^{(1,1)}}^2= \Vert u_m(x,t)-u_{m-1}(x,t)+u_{m-1}(x,t)-u_{m-2}(x,t)+\cdots +u_{n+1}(x,t)-u_n(x,t)\Vert _{W_2^{(1,1)}}^2 \end{aligned}$$
$$\begin{aligned} =\Vert u_m(x,t)-u_{m-1}(x,t)\Vert _{W_2^{(1,1)}}^2+\cdots +\Vert u_{n+1}(x,t)-u_n(x,t)\Vert _{W_2^{(1,1)}}^2 \end{aligned}$$
$$\begin{aligned} =\sum _{i=n+1}^m B_i^2 \rightarrow 0\quad (n \rightarrow \infty ). \end{aligned}$$

Considering that \(W_2^{(1,1)}(D)\) is complete, so it follows

Therefore

$$\begin{aligned} \bar{u}(x,t)= \sum _{i=1}^\infty B_i \bar{\phi }_i(x,t). \end{aligned}$$
(6)

(b) We define the projection operator as follows:

$$\begin{aligned} P_n\bar{u}(x,t)=\sum _{i=1}^n B_i\bar{\phi }_i(x,t). \end{aligned}$$

Thus

$$\begin{aligned} u_{n+1}(x,t)=P_n\bar{u}(x,t). \end{aligned}$$

We claim

$$\begin{aligned} u_{n+1}(x_k,t_k)=\bar{u}(x_k,t_k), k\le n. \end{aligned}$$

To this end, we have

$$\begin{aligned} u_{n+1}(x_k,t_k)=\langle u_{n+1}(x,t), \phi _k(x,t) \rangle _{W_2^{(1,1)}} \end{aligned}$$
$$\begin{aligned} =\langle P_n\bar{u}(x,t),\phi _k(x,t) \rangle _{W_2^{(1,1)}} \end{aligned}$$
$$\begin{aligned} =\langle \bar{u}(x,t),P_n \phi _k(x,t) \rangle _{W_2^{(1,1)}} \end{aligned}$$
$$\begin{aligned} =\langle \bar{u}(x,t), \phi _k(x,t) \rangle _{W_2^{(1,1)}} \end{aligned}$$
$$\begin{aligned} =\bar{u}(x_k,t_k). \end{aligned}$$

Hence

$$\begin{aligned} Fu_{n+1}(x_k,t_k)=F\bar{u}(x_k,t_k),\quad k\le n. \end{aligned}$$

(c) It is obvious that \(\bar{u}(x,t)\) is the solution of Eq. (1). From (6), it follows

$$\begin{aligned} \bar{u}(x_j, t_j)=\sum _{i=1}^ \infty B_i \langle \bar{\phi }_i(x,t), \phi _j(x,t) \rangle _{W_2^{(1,1)}}. \end{aligned}$$
(7)

By multiplying both sides of (7) by \(\alpha _{nj}\) and summing for j from 1 to n, we have

$$\begin{aligned} \sum _{j=1}^n \alpha _{nj} \bar{u}(x_j,t_j)= \sum _{i=1}^\infty B_i \langle \bar{\phi }_i(x,t),\sum _{j=1}^n\alpha _{nj}\phi _j(x,t) \rangle _{W_2^{(1,1)}} \end{aligned}$$
$$\begin{aligned} =\sum _{i=1}^\infty B_i \langle \bar{\phi }_i(x,t),\bar{\phi }_n(x,t) \rangle _{W_2^{(1,1)}}=B_n. \end{aligned}$$
(8)

From (8) and (2), if \(n=1\), then

$$\begin{aligned} \alpha _{11} \bar{u}(x_1,t_1)=B_1=\alpha _{11}(f(x_1,t_1)+Fu_1(x_1,t_1)). \end{aligned}$$

If \(n=2\), then

\(\alpha _{21}\bar{u}(x_1,t_1)+\alpha _{22}\bar{u}(x_2,t_2)=B_2\)

\(=\alpha _{21}(f(x_1,t_1)+Fu_2(x_1,t_1))+\alpha _{22}(f(x_2,t_2)+Fu_2(x_2,t_2))\)

\(=\alpha _{21}(f(x_1,t_1)+F\bar{u}_2(x_1,t_1))+\alpha _{22}(f(x_2,t_2)+Fu_2(x_2,t_2))\)

\(=\alpha _{21}\bar{u}(x_1,t_1))+\alpha _{22}(f(x_2,t_2)+Fu_2(x_2,t_2))\). From the above equality, it follows

$$\begin{aligned} \bar{u}(x_2,t_2)=f(x_2,t_2)+Fu_2(x_2,t_2). \end{aligned}$$

In the same way, we obtain that

$$\begin{aligned} \bar{u}(x_n,t_n)=f(x_n,t_n)+Fu_n(x_n,t_n). \end{aligned}$$

Since \(\{ (x_i,t_i) \}_{i=1}^\infty\) is dense in D, therefore, for any\((y,z)\in D\), there exists a subsequence \(\{ (x_{n_k},t_{n_k}) \}_{k=1}^\infty\) converging to (y, z). From Lemma 3.1 and above equality, we obtain that

$$\begin{aligned} \bar{u}(y,z)=f(y,z)+F\bar{u}(y,z). \end{aligned}$$

Thus, \(\bar{u}(x,t)\) is the solution of Eq. (1) and

$$\begin{aligned} u(x,t) = \sum _{i=1}^ \infty B_i \bar{\phi }_i(x,t). \end{aligned}$$

\(\square\)

Theorem 3.2

Suppose u(x, t) is the solution of Eq. (1) and \(r_n(x,t)\) is the error in the approximate solution \(u_{n+1}(x,t)\), where \(u_{n+1}(x,t)\) is given by (3). Then, \(r_n(x,t)\) is monotone decreasing in the sense of \(\Vert .\Vert _{W_2^{(1,1)}}\).

Proof

If the u(x, t) and \(u_{n+1}(x,t)\) are, respectively, functions in (1) and (6), in this case, we have

$$\begin{aligned} \Vert r_n(x,t)\Vert _{W_2^{(1,1)}}^2 =\Vert u(x,t)-u_{n+1}(x,t)\Vert _{W_2^{(1,1)}}^2 \end{aligned}$$
$$\begin{aligned} =\Vert \sum _{i=n+1}^\infty B_i\bar{\phi }_i(x,t)\Vert _{W_2^{(1,1)}}^2=\sum _{i=n+1}^\infty B_i^2. \end{aligned}$$

This illustrate that the error \(r_n(x,t)\) is monotone decreasing in the sense of \(\Vert .\Vert _{W_2^{(1,1)}}\) [9]. \(\square\)

Numerical examples

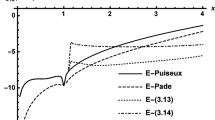
We implement the method presented in this article for some examples. We obtain absolute error of the approximate solution values in the selected points \((x,t)=(\frac{1}{2^i}, \frac{1}{2^i})( i=1,2,\ldots ,6)\). Of course, the choice of points is completely customized. Examples of references listed have been selected, so that we can compare the results in here with results in its references.

Example 4.1

[8] Consider the following nonlinear two-dimensional Volterra integral equation:

$$\begin{aligned} u(x,t)=f(x,t)+\int _0^t \int _0^x (xy^2+\cos {(z)})u^2(y,z) \mathrm{d}y \mathrm{d}z \quad 0\le x,t\le 1 \end{aligned}$$

where

$$\begin{aligned} f(x,t)=x\sin {(t)}(1-\frac{1}{9}x^2\sin ^2{(t))}+\frac{1}{10}x^6\left(\frac{1}{2}\sin {(2t)}-t\right). \end{aligned}$$

The exact solution is \(u(x,t)=x\sin {(t)}\). Table 1 illustrates the numerical results for this example. In addition, for points \((x_i,t_i)=(0.001i,0.001i)\quad( i=1,2,\ldots ,1000)\), the maximum error is as follows:

$$\begin{aligned} M=\max _{i=1,2,\ldots ,1000}\{|r(x_i,t_i)|\}=0.04873005644 \end{aligned}$$

where

$$\begin{aligned} r(x,t)=u(x,t)-u_{30}(x,t). \end{aligned}$$
Table 1 Absolute error of approximate solution for Example 4.1
Full size table

Example 4.2

[7] Consider the following nonlinear two-dimensional Volterra integral equation:

$$\begin{aligned} u(x,t)=f(x,t)+\int _0^t\int _0^x (x+t-z-y)u^2(y,z)\mathrm{d}y\mathrm{d}z\quad 0\le x,\,\,t\le 1 \end{aligned}$$

where

$$\begin{aligned} f(x,t)=x+t-\frac{1}{12}xt(x^3+4x^2t+4xt^2+t^3). \end{aligned}$$

The exact solution is \(u(x,t)=x+t\). Table 2 illustrates the numerical results for this example. In addition, for points \((x_i,t_i)=(0.001i,0.001i)( i=1,2,\ldots ,1000)\), the maximum error is as follows:

$$\begin{aligned} M=\max _{i=1,2,\ldots ,1000}\{|r(x_i,t_i)|\}=0.165027043 \end{aligned}$$

where

$$\begin{aligned} r(x,t)=u(x,t)-u_{40}(x,t). \end{aligned}$$
Table 2 Absolute error of approximate solution for Example 4.2
Full size table

Example 4.3

[8] Consider the following nonlinear two-dimensional Volterra integral equation:

$$\begin{aligned} u(x,t)=f(x,t)+\int _0^t\int _0^x u^2(y,z) \mathrm{d}y\mathrm{d}z\quad (x,t)\in [0,1)\times [0,1) \end{aligned}$$

where

$$\begin{aligned} f(x,t)=x^2+t^2-\frac{1}{45}xt(9x^4+10x^2t^2+9t^4). \end{aligned}$$

The exact solution of this problem is \(u(x,t)=x^2+t^2\). Table 3 illustrates the numerical results for this example. In addition, for points \((x_i,t_i)=(0.001i,\,0.001i)\,( i=1,2,\ldots ,1000)\), the maximum error is as follows:

$$\begin{aligned} M=\max _{i=1,2,\ldots ,1000}\{|r(x_i,t_i)|\}=0.3099048997 \end{aligned}$$

where

$$\begin{aligned} r(x,t)=u(x,t)-u_{30}(x,t). \end{aligned}$$
Table 3 Absolute error of approximate solution for Example 4.3
Full size table

Conclusion and comments

This paper deals with a computational method for approximate solution of Volterra integral equations of the second kind based on the expansion of the solution as series of reproducing kernel functions. The advantage of the present method (compared with methods based on basis sets of different kinds) is not limitation on the nonlinear term. Considering that absolute errors of approximate solution in given points are small enough, so it follows that the presentation method in this article is right. The codes were written in Maple. We think that this method can be generalized to the new inner multiply that it provides reproducing kernel space.