Parameter estimation of some Kumaraswamy-G type distributions

Abstract

Since Kum-G distributions have additional two parameters, the estimation of parameters becomes an interesting problem by itself. In this study, we consider parameter estimation of Kum-Weibull, Kum-Pareto and Kum-Power distributions by using the maximum likelihood and the maximum spacing methods. These three distributions are important in reliability and other applications. The Kum-Pareto and Kum-Power distributions have parameter-dependent boundaries, which makes the estimation of parameters more interesting. We performed simulations for each of these considered distributions by using the R software for estimating parameters using the maximum likelihood and the maximum spacing method. In addition, an application of these distribution families to real data for modeling wind speed in a particular location in Turkey is discussed.

Introduction

In 1980, Kumaraswamy [11] introduced a new distribution with applications in hydrology. The cumulative distribution function (cdf) of this new distribution is given by

$$\begin{aligned} F(x)=1-\left( 1-x^{a} \right) ^{b}, \quad 0<x<1, \end{aligned}$$

(1)

where $a>0$ and $b>0$. Jones [10] discussed properties of the Kumaraswamy distribution and its similarities with the beta distribution.

In recent years one can find many papers which generalize this distribution by replacing x with some known distribution such as normal, Weibull, Pareto, and others (see, for example [2, 9, 12]). Based on the Kumaraswamy distribution Cordeiro and Castro [6] introduced a new generalized family of distributions, denoted in this paper by Kum-G, and discussed its basic statistical properties and application to a real data set.

It can be seen that in recent years many authors study applications and parameter estimation of special Kum-G distributions. For example, Cordeiro et al. [9] investigate the Kum-Weibull model and its application to failure data. Tamandi and Nadarajah [16] discuss parameter estimation of the Kum-Weibull, Kum-Normal and Kum-Inverse Gaussian families.

Since Kum-G distributions have additional two parameters, the estimation of parameters becomes an interesting problem by itself. The maximum likelihood method (ML) is one of the preferred methods for estimating the parameters in Kum-G distributions. Tamandi and Nadarajah [16] consider also the maximum spacing method (MSP) and compare it with the maximum likelihood (ML) method for estimating the parameters in some of the Kum-G distributions.

It is known that in situations like mixtures of distributions and distributions with a parameter-dependent lower bound, where the ML estimator leads to inconsistent estimators, the MSP estimator is consistent; see [13]. Motivated by this fact it is natural to consider the MSP estimator in parameter estimation for the Kum-Pareto and Kum-Power distributions.

In this study, we consider parameter estimation of the Kum-Weibull [6], Kum-Pareto [2] and Kum-Power [12] families of distributions by using the ML and MSP methods. Although one may find some studies for the Kum-Weibull and Kum-Pareto distributions, there is only one paper dealing with the Kum-Power family of distributions. We performed simulations for each of the considered family of distributions. For calculations we used the R software [14]. In particular, for estimating parameters in the simulations the optim function in R was applied with the Nelder–Mead method. The parameter estimates for the Weibull distribution were obtained by applying the fitdistr method in R.

It can be seen from the literature that wind speed can be modeled by various distributions such as Weibull, Rayleigh, gamma, lognormal, beta, Burr, and inverse Gaussian distributions, among others [17]. For example, Chang [3] compared the performance of six numerical methods in estimating Weibull parameters for wind energy application. He concludes that the maximum likelihood, modified maximum likelihood and moment methods show better performance in simulation tests. In this study, we consider modeling wind speed by using the following generalized families of distributions: Kum-Weibull and Kum-Power. We note here that, for example, the Kum-Weibull family of distributions includes the Weibull and Rayleigh distributions. It is expected that the flexibility of the two additional two parameters in the Kum-G family of distributions will improve the modeling results. The parameter estimates for the real data were obtained by applying the ga method [15], which is a genetic algorithm method implemented in R.

Kumaraswamy distributions considered

Cordeiro and Castro [6] introduced a new generalized family of distributions by replacing x with a continuous base line distribution G(x) in Kumaraswamy’s distribution:

$$\begin{aligned} F(x)=1-\left\{ 1-G^{a}(x)\right\} ^{b}, \end{aligned}$$

(2)

$$\begin{aligned} f(x)=ab \, g(x) \, G^{a-1}(x) \left( 1-G^{a}(x) \right) ^{b-1}, \end{aligned}$$

(3)

where g is the probability density function (pdf) of G and $a>0$, $b>0$.

The cdf of the Kum-Weibull distribution is given by

$$\begin{aligned} F(x) = 1 - \left( 1 - \left[ 1 - e^{-(\lambda x)^c} \right] ^a \right) ^b, \end{aligned}$$

(4)

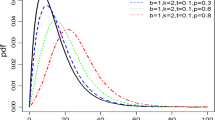
where $a > 0$, $b > 0$, $\lambda > 0$ and $c > 0$. We will denote this distribution by Kum-W$(a, b, \lambda , c)$. Some special cases of the Kum-W$(a, b, \lambda , c)$ are given in Table 1 [6]. Figure 1 shows some special cases of the density function for this family.

Table 1 Some Kum-W special cases

Fig. 1

Some Kum-Weibull distributions

The cdf of the Kum-Pareto distribution is

$$\begin{aligned} F(x) = 1 - \left( 1 - \left[ 1 - \left( \frac{\beta }{x} \right) ^k \right] ^a \right) ^b, \end{aligned}$$

(5)

where $a > 0$, $b > 0$, $\beta > 0$ and $k > 0$. We will denote this distribution by Kum-Par$(a, b, \beta , k)$. Figure 2 shows some special cases of Kum-Pareto density functions.

Fig. 2

Some Kum-Pareto distributions

The cdf of the Kum-Power distribution is given by

$$\begin{aligned} F(x) = 1 - \left( 1 - \left[ \left( \frac{x}{\beta } \right) ^{\alpha } \right] ^a \right) ^b \end{aligned}$$

(6)

where $a > 0$, $b > 0$, $\alpha > 0$ and $\beta > 0$. We will denote this distribution by Kum-Pow$(a, b, \alpha , \beta )$. Figure 3 shows some special cases of Kum-Power density functions.

Fig. 3

Some Kum-Power distributions

Parameter estimation

The ML method is one of the most widely used parameter estimation methods in statistics. On the other hand, it is known that ML estimation may lead to inconsistent estimation results, especially in parameter-dependent boundary situations. Ranneby [13] showed that in such cases, the maximum spacing method is more reliable than the ML method. Ekström [7, 8], on the other hand, showed that the MSP estimators may give better results than ML estimators for small samples. Also, Cheng [4] showed that in unbounded likelihood problems such as estimation of three-parameters in the Weibull distribution, the MSP estimation method produces consistent and asymptotically efficient estimators. Recently, Tamandi and Nadarajah [16] investigated parameter estimation of some Kum-G distributions by using ML and MSP methods.

In this paper, we consider parameter estimation of the Kum-Weibull, Kum-Pareto and Kum-Power distributions by using ML and MSP methods. We note that in Kum-Par as well as Kum-Pow distributions parameter-dependent boundaries exist. Therefore, we hope that this study will contribute to parameter estimation in Kum-G distributions.

Since by definition of the Kum-G distributions two additional shape parameters are introduced to the family of $G(x,{{\varvec {\theta }}})$ distributions, the estimation of parameters becomes an interesting problem. The additional two parameters a and b provide more flexibility in modeling and applications. On the other hand, it should be noted that this flexibility also causes some major problems in parameter estimation. It can be seen that one of the main problems is that one may have to deal with quite different support sets of the distribution for different parameter values. Thus classical hill-climbing approaches such as Newton–Raphson and as well as methods such as Nelder–Mead may actually not give consistent (or any) results in Kum-G distributions.

Maximum likelihood method

To obtain the ML and MSP formulations for Kum-G distributions suppose that $X_1, X_2,\ldots , X_n$ is a random sample from some Kum-G distribution $G(x, {\varvec {\theta }})$ with pdf given by (3) and baseline pdf g. Also suppose that g is parameterized by a vector ${\varvec {\theta }}$ of length p. The log-likelihood function of a, b and ${\varvec {\theta }}$ is

$$\begin{aligned} l(a,b, {\varvec {\theta }} )&= n \log a+n \log b+ \sum _{ i=1}^n \log g(x_i,{\varvec {\theta }} )+(a-1) \sum _{ i=1}^n \log G(x_i, {\varvec {\theta }} ) \nonumber \\&\quad +(b-1) \sum _{ i=1}^n \log \left[ 1 - G^a(x_i, {\varvec {\theta }} )\right] \end{aligned}$$

(7)

The ML estimates of the parameters can be found by solving the following equations simultaneously:

$$\begin{aligned} \frac{n}{a}+\sum _{ i=1}^n \log G(x_i,{\varvec {\theta }} )-(b-1)\sum _{ i=1}^n \frac{G^a (x_i,{\varvec {\theta }} ) \log G(x_i,{\varvec {\theta }} )}{1-G^a (x_i,{\varvec {\theta }} )}=0, \end{aligned}$$

$$\begin{aligned} \frac{n}{b}+\sum _{ i=1}^n \log \left[ 1- G^a(x_i,{\varvec {\theta }} )\right] =0, \end{aligned}$$

and

$$\begin{aligned} \sum _{ i=1}^n \frac{1}{g(x_i,{\varvec {\theta }} )}\frac{\partial g(x_i,{\varvec {\theta }} )}{\partial \theta _k}-(a-1)\sum _{ i=1}^n \frac{1}{G(x_i,{\varvec {\theta }} )} \frac{\partial G(x_i,{\varvec {\theta }} )}{\partial \theta _k} \nonumber \\ -a(b-1)\sum _{ i=1}^n \frac{ G^{a-1}(x_i,{\varvec {\theta }} )}{1-G^a(x_i,{\varvec {\theta }} )} \frac{\partial G(x_i,{\varvec {\theta }} )}{\partial \theta _k}=0. \end{aligned}$$

(8)

It should be noted that in order to find numerical solutions by using the above formulae, one has to calculate among other functions, $g(x,{\varvec {\theta }})$ for different parameter vectors ${\varvec {\theta }}$, which may stop the iterations of the algorithm because $g(x,{\varvec {\theta }})$ may not be defined for the corresponding ${\varvec {\theta }}$ vector. Since in (8) the first term includes the reciprocal of $g(x,{\varvec {\theta }})$ some algorithms may not converge or even work in this case. By considering how the MSP method (see Eq. (11)) is obtained, one may observe that this type of problem is less likely to occur in MSP.

Maximum spacing method

The MSP method was introduced by Cheng [4] as an alternative to the ML method. Ranneby [13] derived the MSP method from an approximation of the Kullback–Leibler divergence (KLD). Cheng [4] showed that in unbounded likelihood problems such as estimation of three-parameter gamma, lognormal or Weibull distributions, the MSP estimation method produces consistent and asymptotically efficient estimators. In situations like mixtures of distributions and distributions with a parameter-dependent lower bound, where the MLE leads to inconsistent estimators, the MSP estimator is consistent; see [13]. Even in other situations, Ekström [8] showed that the MSP estimators have better properties than ML estimators for small samples. Ekström [8] showed that MSP estimators are L1-consistent for any unimodal pdf without any additional conditions. According to [13], the MSP method works better than the ML method for multivariate data too. MSP estimators have all the nice properties of ML estimators such as consistency, asymptotic normality, efficiency and invariance under one-to-one transformations. For a detailed survey of the MSP method, the reader is referred to [8]. On the other hand, MSP estimators have some disadvantages too. First of all, they are sensitive to closely spaced observations, and especially ties. They are also sensitive to secondary clustering: one example is when a set of observations is thought to come from a single normal distribution, but in fact comes from a mixture of normals with different means [5].

Let $x_1, x_2,\ldots ,x_n$ be a random sample from a population with cdf $F(x,{\varvec {\theta }})$ and let $f(x,{\varvec {\theta }})$ denote the corresponding pdf. The Kullback–Leibler divergence between $F(x,{\varvec {\theta }})$ and $F(x,{\varvec {\theta }}_0)$ is given by

$$\begin{aligned} H(F_{{\varvec {\theta }}}, F_{{\varvec {\theta }}_0})=\int f(x,{\varvec {\theta }}_0) \log \left| \frac{f(x,{\varvec {\theta }}_0)}{f(x,{\varvec {\theta }})}\right| \mathrm{{d}}x \end{aligned}$$

The KLD can be approximated by estimating $H(F_{{\varvec {\theta }}}, F_{{\varvec {\theta }}_0})$ by

$$\begin{aligned} \frac{1}{n} \sum _{ i=1}^n \log \left| \frac{f(x_i,{\varvec {\theta }}_0)}{f(x_i,{\varvec {\theta }})}\right| \end{aligned}$$

(9)

Minimizing (9) with respect to ${\varvec {\theta }}$, the estimator of ${\varvec {\theta }}_0$ can be found, which is actually the well-known MLE. It should be noted that for some continuous distributions, $\log f (x_i)$, $i = 1,\ldots , n$ may not be bounded from above. Ranneby [13], therefore, suggested another approximation of the KLD, namely

$$\begin{aligned} \frac{1}{n+1} \sum _{ i=1}^{n+1} \log \left| \frac{F(x_{(i)}, {\varvec {\theta }}_0)-F(x_{(i-1)},{\varvec {\theta }}_0)}{F(x_{(i)}, {\varvec {\theta }})-F(x_{(i-1)}, {\varvec {\theta }})}\right| , \end{aligned}$$

(10)

where $x_{(i-1)}\le x_{(i-1)}\le \cdots \le x_{(i-1)}$ are the order statistics and $F(x_{(0)},{\varvec {\theta }})\equiv 0$, $F(x_{(n+1)}, {\varvec {\theta }})\equiv 1$. $F(x_{(i)},{\varvec {\theta }}_0)-F(x_{(i-1)}, {\varvec {\theta }})$ are the first-order spacings of $F(x_{(0)}, {\varvec {\theta }}_0), \ldots , F(x_{(n+1)}, {\varvec {\theta }})$.

By minimizing (10) the MSP estimator of ${\varvec {\theta }}_0$ is obtained. Minimizing (10) is equivalent to maximizing:

$$\begin{aligned} M({\varvec {\theta }}) = \sum _{ i=1}^{n+1} \log \left[ F(x_{(i)}, {\varvec {\theta }})-F(x_{(i-1)}, {\varvec {\theta }})\right] , \end{aligned}$$

(11)

where ${\varvec {\theta }}$ is an unknown parameter. Therefore, the MSP estimator can obtained by maximizing $M({\varvec {\theta }})$ with respect to ${\varvec {\theta }}$.

Consider estimation of some Kum-G distribution with baseline distribution G by the MSP method. Suppose that $x_{(1)}, x_{(2)},\ldots , x_{(n)}$ is an ordered sample and $x_{(0)}=0, x_{(n+1)}=\infty$. These values for $x_{(0)}$ and $x_{(n+1)}$ assume that the support for G is the positive real line. If the support for G is different, then $x_{(0)}$ and $x_{(n+1)}$ can be chosen accordingly. Substituting (2) into (11) we obtain

$$\begin{aligned} M(a,b, {\varvec {\theta }}) = \sum _{ i=1}^{n+1} \log \left\{ \left( 1-G^a (x_{(i-1)}, {\varvec {\theta }})\right) ^b-(1-G^a (x_{(i)}, {\varvec {\theta }}))^b\right\} . \end{aligned}$$

(12)

To find the ML estimates of the parameters, the simultaneous solutions of the equations obtained by taking partial derivatives with respect to the parameters a, b and ${\varvec {\theta }}$ have to be found. It should be noted that, in general, no analytical solution exists for these equations. Therefore, numerical methods need to be applied in order to find the corresponding parameter estimates.

Simulation results

Simulation is a powerful tool that is used in many areas of science. For example, some recent simulation studies can be found in [1, 18]. Abbasbandy and Shivanian [1] used numerical simulation based on meshless technique to study the biological population model. Vajargah and Shoghi [18] used quasi-Monte Carlo method in prediction of total index of stock market and value at risk. To assess the performance of the ML and MSP estimators we conducted a small size simulation study for the Kum-W, Kum-Par and Kum-Pow distributions. It should be noted that these three Kum-G distributions have different characteristics and are also important in reliability problems and applications. The Kum-Par and Kum-Pow distributions both have parameter-dependent boundaries, which may have important implications in parameter estimation. We used 1000 runs in each simulation to compare estimation results for the estimators. In this study, we selected a sample size of $n=25$.

In order to include the effect of initial values in the estimates, we used randomly generated starting values as follows. Let Kum-G$(a, b, \theta _1, \theta _2)$ be one of the considered Kum-G distributions, where G is one of the Weibull, Pareto or Power distributions and $\theta _1$ and $\theta _2$ are the corresponding parameters. We generated random variates from Kum-G$(a_0, b_0, {\theta _1}^0, {\theta _2}^0)$ and as starting values the following values were used:

$$\begin{aligned} a_0 + u_1, \; u_1 \in U\left( -\frac{a_0}{2}, \frac{a_0}{2} \right) \\ b_0 + u_2, \; u_2 \in U\left( -\frac{b_0}{2}, \frac{b_0}{2} \right) \\ {\theta _1}^0 + u_3, \; u_3 \in U\left( -\frac{{\theta _1}^0}{2}, \frac{{\theta _1}^0}{2} \right) \\ {\theta _2}^0 + u_4, \; u_4 \in U\left( -\frac{{\theta _2}^0}{2}, \frac{{\theta _2}^0}{2} \right) \end{aligned}$$

Table 2 Bias and MSE for sample size $n=25$ (1000 runs)

Table 2 shows that, in general, MSP estimates have smaller bias and MSEs. When a is considerably larger than b significant differences between the two estimates are observed. Also for $a=10$ we observed some convergence problems related to the initial parameters in the ML method. Therefore, only 1000 iterations were conducted in the simulations. We note that this problem did not occur in the MSP method.

Table 3 Bias and MSE for sample size $n=25$ (1000 runs)

When $a<b$ (that is for heavy-tailed) and for fixed a with increasing b Table 3 shows that the MSEs for MSP are smaller then for MLE. On the other hand, when a is considerably larger than b significant differences between the two estimates are observed. In the remaining cases no significant differences are observed.

Table 4 Bias and MSE for sample size $n=25$ (1000 runs)

From Table 4 it can be observed that MLE, in general, outperforms MSP estimates. This can be explained by the fact that for the Kum-Pow distribution closely spaced observations are much more likely to occur. It is known that MSP is sensitive to closely spaced observations.

It should be noted that estimating all four parameters in the Kum-G families of distributions may result in inconsistent estimates. In addition, it can be observed that the estimates are highly dependent on the initial values which may also lead to convergence problems. For this reason when applying these families of distributions to real data, we preferred to use genetic algorithms for estimating the parameters.

Application to real data

Wind energy is an important alternative to conventional energy resources. Therefore, one may find many studies related to modeling wind characteristics such as wind speed in order to estimate the potential for use in generating energy. It can be observed that distributions such as Weibull, Rayleigh, gamma, lognormal, beta, Burr, and inverse Gaussian distributions are used in modeling wind speed frequencies [17]. As noted before, the two additional parameters in the Kum-G distribution families may provide more flexibility in modeling. For example, the Kum-Weibull family of distributions include the Weibull and Rayleigh distributions as special cases. Motivated by this fact the Kum-Weibull, Kum-Pareto and Kum-Power families of distributions are applied to model wind speed frequencies for a particular location, Cide, in Turkey. The data represent daily average wind speed measurements at the given location for January 2016 and are obtained from the Turkish State Meteorological Service.

The results for the wind data are given in Table 5 and in Fig. 4. The parameter estimates for the Weibull distribution are obtained by applying the fitdistr method in R. The parameter estimates for the Kum-W and Kum-Pow distributions were obtained by applying the ga method ([15]), which is a genetic algorithm method implemented in R. Since in this particular application the Kum-Pareto families of distributions are not suited for the data we did not include the results for Kum-Pareto. On the other hand, due to convergence problems with ML estimation, only results for the MSP method with genetic algorithms are given. Table 5 clearly demonstrates that Kum-G families of distributions can be used as alternatives for classical distributions such as Weibull. Since many types of distributions, for example, are used in modeling wind characteristics it should be expected that Kum-G families of distributions may improve modeling results.

Fig. 4

Parameter estimates for wind data

Table 5 Parameter estimates fitted to wind data

Conclusion

Tamandi and Nadarajah [16] considered parameter estimation of Kum-Weibull, Kum-Normal and Kum-InverseNormal distributions. They stated that for these distributions, in general, the MSP method results in smaller bias and MSEs for small sample sizes. It should be noted that in these distributions no parameter-dependent boundaries exist, that is the domain of the random variable is independent of the parameters. In this study, we considered three Kum-G distributions, all with different characteristics. The Kum-Par and Kum-Pow distributions both have parameter-dependent bounds and may model different distributions. In addition, we applied these families of distributions to model real data for wind speed measurements.

The computations in the simulations and in application to real data have shown that the MSP method, in general, outperforms the ML method. Also, we have seen that in the ML method the initial values for parameters may cause the algorithms to stop before reaching any feasible parameter estimate. Thus, in general the ML approach is sensitive to initial values leading to convergence problems. In contrast, the MSP method, in general, seems to give more consistent results. Therefore, to model wind speed we have preferred to use genetic algorithms with the MSP approach in order to obtain parameter estimates for the Kum-W and Kum-Pow families of distributions.