An improved adaptation of homotopy analysis method

Abstract

An improved adaptation of the well-known homotopy analysis method (HAM) is proposed to approximate the solutions of strongly nonlinear differential problems in terms of a rapidly convergent series. The proposed method involves simpler integrals and less computations than the standard HAM. The method is illustrated using different numerical examples. The comparative analysis confirms the applicability and efficiency of the proposed technique.

Introduction

Liao [1] proposed an approximate analytical technique namely homotopy analysis method (HAM) built on the concept of homotopy for the solutions of nonlinear differential equations. The homotopy analysis is not only an efficient method to solve highly nonlinear differential equation problems but also allows great freedom to choose the initial approximation and is highly flexible in many respects so that it might overcome restrictions of perturbation techniques and other non-perturbation methods. The great freedom and flexibility of the HAM has inspired many mathematicians to attack HAM in search of better numerical techniques. Marinca and Herisanu [2] proposed optimal homotopy asymptotic method to investigate the solutions of nonlinear equations arising in heat transfer. Motsa et al. [3] introduced a new spectral-homotopy analysis method for solving a nonlinear second order BVP. Homotopy analysis method has been successfully applied to investigate the solutions of integral equations [4]. Abbasbandy and Shivanian [5] proposed predictor homotopy analysis method (PHAM) to predict the multiplicity of the solutions of some nonlinear boundary value problems. Shivanian et al. [6] used PHAM to study a case of boundary layer flows. They proved the existence of multiple solutions and also calculated the approximate solutions. Vosoughi et al. [7] also used PHAM to obtain two approximate solutions in a study of nonlinear reactive transport model. Abbasbandy et al. [8] studied the role of convergence-control parameter in homotopy analysis method. Motsa et al. [9] proposed an improved spectral homotopy analysis method for MHD flow in a semi-porous channel. Shaban et al. [10] proposed a Tau modification of the homotopy analysis method to study the magneto-hydrodynamic squeezing flow between two parallel disks with suction or injection. Shivanian and Abbasbandy [11] discussed PHAM for two points second order boundary value problems. Homotopy analysis method has been applied in a study of combined conduction–convection–radiation heat transfer [12]. Odibat and Bataineh constructed homotopy polynomials by introducing an adaptation of HAM [13]. In the present paper, an improved adaptation of homotopy analysis method is proposed for the numerical solution of differential equations.

Higher order boundary value problems are studied due to their mathematical importance and applications in different physical phenomena. Mathematical modeling of AFTI-F16 fighters involves ninth order differential equation [14]. Ninth order boundary value problems also arise in the study of of astrophysics, hydrodynamic, and hydromagnetic stability [15, 16]. The study of hydrodynamic and hydromagnetic stability also involves eighth and tenth order boundary value problems [17]. The mathematical importance of boundary value problems of higher order motivates to study different mathematical techniques to obtain the solutions of these problems. Siddiqi and Twizell [18–21] presented the solutions of 6th, 8th, 10th, and 12th order boundary value problems using 6th, 8th, 10th, and 12th degree splines, respectively. Inc and Evans [22] used Adomian decomposition method to approximate solutions of eighth order boundary value problems. Siddiqi and Akram [23–27] presented the solutions of 5th, 6th, 8th, 10th, and 12th order boundary value problems using nonpolynomial spline techniques. Hassan and Erturk [28] applied differential transformation method to obtain the solution of some linear and nonlinear higher order boundary value problems. Siddiqi and Iftikhar [29] used the variational iteration method to approximate the solution of seventh order boundary value problems in terms of a convergent series. Hakeemullah et al. [30] used the optimal homotopy asymptotic method (OHAM) for approximating the solution of modified Kawahara equations. The proposed method is numerically illustrated for the solutions of different higher order boundary value problems. Viswanadham and Ballem [31] used Galerkin method with septic B-splines to approximate the solution of tenth order boundary value problems.

Homotopy analysis method

Homotopy analysis method is an analytical technique which can be used to compute the solutions of linear and nonlinear differential equations. The solution is obtained in terms of a convergent series. Consider a nonlinear differential equation

$$\begin{aligned} N[y(x)]=0, \quad x\in \Theta , \end{aligned}$$

(1)

where N is a nonlinear operator, x is an independent variable, y(x) is an unknown function, and $\Theta$ is the interval of domain. A homotopy Y(x, p) can be constructed with an embedding parameter $p\in [0,1]$ by

$$\begin{aligned} (1-p)L[Y(x,p)-y_0(x)]-phH(x)N[Y(x,p]=0,\quad x\in \Theta , \end{aligned}$$

(2)

where h is auxiliary parameter, H(x) is an auxiliary function, and L is auxiliary linear operator. The homotopy analysis allows great freedom to select h, H(x), and L. Also there is larger freedom to choose the initial approximation $y_0(x)$. For suitable selection, the unknown function Y(x, p) can be determined. Moreover, the mth-order derivative of $y_0(x)$ with respect to the embedding parameter exists at $p=0$ for all positive integral values of m. This quantity is the so-called mth-order deformation derivative. Application of Taylor’s theorem gives the series expansion of Y(x, p) as

$$\begin{aligned} Y(x,p)=y_0(x)+\sum _{m=1}^{\infty }y_m(x)p^m, \end{aligned}$$

(3)

where $y_m(x)$ is obtained by dividing the mth-order deformation derivative by m!. For suitably chosen H(x), h, L, and $y_0(x)$, the series converges to y(x) at $p=1$. Moreover, $y_m(x), m=1,2,3,\ldots$ can be calculated using the mth-order deformation equation

$$\begin{aligned} L[y_m(x)-\chi _{m}y_{m-1}(x)]-h H(x)R_{m}(\underline{y}_{m-1})=0,\\ \quad x\in \Theta , \quad p\in [0,1],\nonumber \end{aligned}$$

(4)

where

$$\begin{aligned}&R_{m}(\underline{y}_{m-1})=\frac{1}{(m-1)!}\left. \frac{\partial ^{m-1}N(Y(x,p))}{\partial p^{m-1}}\right| _{p=0},\nonumber \\&\underline{y}_{m-1}(x)=\{y_{0}(x),y_{1}(x),\ldots ,y_{m-1}(x)\},\quad \quad \nonumber \\&\chi _{m}=\left\{ \begin{array}{ll} 0,\quad m\le 1,\\ 1,\quad m>1. \end{array} \right. \end{aligned}$$

(5)

An improved adaptation of homotopy analysis method

Recently, Odibat and Bataineh [13] have presented an adaptation of homotopy analysis method for solving strongly nonlinear problems. The technique not only reduces the number of terms involved in each iteration but also overcomes the difficulty faced in solving complicated integrals. The adaptation is based on the assumption that the nonlinear operator N can be expressed as a power series in the dependent variable. The method can be easily implemented on equations of the form

$$\begin{aligned} N(y)=f(y) \end{aligned}$$

but needs some extra calculation for equations of the form

$$\begin{aligned} N(y)=f(x,y). \end{aligned}$$

In the present paper, the adaptation is improved to obliterate the need for extra calculations. The improved adaptation is based on the assumption that a power series expansion of the nonlinear operator N can be expressed as

$$\begin{aligned} N(y)=\sum _{i=0}^{\infty }c_{i}x^{i}, \end{aligned}$$

(6)

where $c_{i}$’s are real numbers. Using the fact that HAM yields the solution of Eq. (1) in terms of a power series as

$$\begin{aligned} Y(x,p)=\sum _{i=0}^{\infty }y_{i}p^{i}, \end{aligned}$$

(7)

The modified homotopy $\hat{Y}(x,p)$ can be constructed with an embedding parameter $p\in [0,1]$ by

$$\begin{aligned} (1-p)L\left[ \sum _{i=0}^{\infty }y_{i}p^{i}-y_0(x)\right] -phH(x)\sum _{i=0}^{\infty }c_{i}x^{i}p^{i}=0,\quad x\in \Theta , \end{aligned}$$

(8)

where h is auxiliary parameter, H(x) is an auxiliary function, and L is auxiliary linear operator. The first few modified higher order deformation equations are expressed as

$$\begin{aligned} \left\{ \begin{array}{l} L[y_{1}(x)] = hH(x)c_{0},\\ L[y_{2}(x)] = L[y_{1}(x)]+hH(x)c_{1}y_{0},\\ L[y_{3}(x)] = L[y_{2}(x)]+hH(x)(c_{1}y_{1}+c_{2}y_{0}^{2}),\\ L[y_{4}(x)] = L[y_{3}(x)]+hH(x)(c_{1}y_{2}+2c_{2}y_{0}y_{1}+c_{3}y_{0}^{3}). \end{array} \right. \end{aligned}$$

In the next section, the proposed method is numerically illustrated using different linear and nonlinear higher order boundary value problems.

Numerical examples

Example 1

For $x\in [0,1]$, the following ninth order nonlinear boundary value problem is considered

$$\begin{aligned} \left. \begin{array}{l} y^{(9)}(x)-y(x)y'(x)=e^{-2 x}(2+e^{x}(x-10)-3 x+x^{2}),\\ y(0)=1, \quad y(1)=0,\\ y'(0)=-2,\quad y'(1)=-e^{-1},\\ y''(0)=3,\quad y''(1)=2e^{-1},\\ y'''(0)=-4,\quad y'''(1)=-3e^{-1},\\ y^{(4)}(0)=5. \end{array} \right\} \end{aligned}$$

(9)

Fig. 1

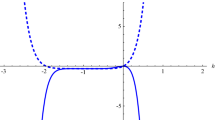
Comparison of exact solution (solid line) and approximate solution (dashed line) for Example 1

Fig. 2

Absolute errors for Example 1

The analytic solution of this differential system is

$$\begin{aligned} y(x)=(1-x)e^ {-x}. \end{aligned}$$

According to basic assumption of HAM, the initial approximation is chosen as

$$\begin{aligned} y_{0}(x)= & {} \frac{1}{24e}(24e-48e x + 36e x^{2} -16e x^{3} +5e x^{4} + 660 x^{5} - 244e x^{5} - 1788 x^{6 }+ 658e x^{6} \nonumber \\&+ 1620 x^{7} - 596e x^{7} - 492 x^{8} +181 x^{8}). \end{aligned}$$

(10)

The first, second, and third order deformation equations are obtained as

$$\begin{aligned} \left\{ \begin{array}{l} L[y_{1}(x)] = 10hH(x),\\ L[y_{2}(x)] = L[y_{1}(x)]-11hH(x)y_{0},\\ L[y_{3}(x)] = L[y_{2}(x)]+hH(x)(-11y_{1}+6y_{0}^{2}). \end{array} \right. \end{aligned}$$

Solving these differential equations for $y_{1}(x)$, $y_{2}(x)$ and $y_{3}(x)$, the third order approximation to the solution is calculated. Here, the auxiliary function H(x) is taken as $H(x)=1$ and the linear operator is chosen to be the homogeneous part of the nonlinear operator N.

Table 1 Numerical results for Example 1

Table 1 shows the approximate solution and corresponding absolute error values using the proposed method for $h=-0.2$. The comparison of the exact solution and the approximate solution is shown in Fig. 1 and the graph of absolute errors over the interval of domain is shown in Fig. 2.

Example 2

The following ninth order linear boundary value problem is considered, as

$$\begin{aligned} \left. \begin{array}{l} y^{(9)}(x)- y(x)=-9 e^{x},\quad x\in {[0,1]}\\ y(0)=1,\quad y(1)=0,\\ y'(0)=0,\quad y'(1)=-e,\\ y''(0)=-1,\quad y''(1)=-2e,\\ y'''(0)=-2,\quad y'''(1)=-3e,\\ y^{(4)}(0)=-3. \end{array} \right\} \end{aligned}$$

(11)

Fig. 3

Comparison of exact solution (solid line) and approximate solution (dashed line) for Example 2

Fig. 4

Absolute errors for Example 2

The analytic solution of this differential system is

$$\begin{aligned} y(x)=(1-x)e^{x}. \end{aligned}$$

The initial approximation is calculated using the standard HAM, as

$$\begin{aligned} y_{0}(x) &= 1 - \frac{x^{2}}{2}-\frac{ x^{3}}{3} - \frac{x^{4}}{8} + \frac{1}{24}(-1012+ 372e)x^{5} + \frac{1}{24}(2642 - 972e)x^{6 }\nonumber \\ & \quad + \frac{1}{24}(-2316+ 852e)x^{7} + \frac{1}{24}(685 - 252e)x^{8}. \end{aligned}$$

(12)

First, second, and third order deformation equations are obtained, as

$$\begin{aligned} \left\{ \begin{array}{l} L[y_{1}(x)] = 8hH(x),\\ L[y_{2}(x)] = L[y_{1}(x)]+9hH(x)y_{0},\\ L[y_{3}(x)] = L[y_{2}(x)]+hH(x)(9y_{1}+5y_{0}^{2}). \end{array} \right. \end{aligned}$$

The third order approximation to the solution is calculated by solving these differential equations for $y_{1}(x)$, $y_{2}(x)$ and $y_{3}(x)$. Here, the auxiliary function H(x) is taken as $H(x)=1$. For this choice of function, higher accuracy can be achieved without having to go to higher order of approximation. The linear operator is chosen to be the homogeneous part of the nonlinear operator N. The approximate solution and corresponding absolute error values, for $h=-0.2$, are summarized in Table 2.

Table 2 Numerical results for Example 2

Table 3 Comparison of maximum absolute error with DTM

Table 3 shows that the proposed method gives better results than differential transformation method [28].

Example 3

The following ninth order nonlinear boundary value problem is considered as

$$\begin{aligned} \left. \begin{array}{llllll} y^{(9)}(x)e^{y(x)}=0,\quad \quad x\in {[0,1]},\\ y(0)=0,~y(1)=\sin (1),\\ y'(0)=0,~y'(1)=\cos (1)+\sin (1),\\ y''(0)=2,~y''(1)=2\cos (1)-\sin (1)+,\\ y'''(0)=0,~y'''(1)=-\cos (1)-3\sin (1),\\ y^{(4)}(0)=-4. \end{array} \right\} \end{aligned}$$

(13)

The analytic solution of this differential system is

$$\begin{aligned} y(x)=x\sin (x). \end{aligned}$$

The initial approximation is calculated according to the standard HAM, as

$$\begin{aligned} y_{0}(x)&= x^{2}-\frac{x^{4}}{6}+\frac{1}{6}x^{6}(264+231\cos (1)- 462\sin (1))+\frac{1}{6}x^{8}(59+59\cos (1)-108\sin (1))\nonumber \\&\quad + \frac{1}{6}x^{5}(-116- 89\cos (1)+195\sin (1))+\frac{1}{6}x^{7}(-212- 201\cos (1)+381\sin (1)). \end{aligned}$$

(14)

The third order approximation to the exact solution is calculated using the improved adaptation proposed in the present paper. The approximate solution values and corresponding absolute errors are shown in Table 4.

Fig. 5

Comparison of exact solution (solid line) and approximate solution (dashed line) for Example 3

Fig. 6

Absolute errors for Example 3

Table 4 Numerical results for Example 3

The auxiliary function H(x) is taken as $H(x)=1$. The linear operator is chosen to be the homogeneous part of the nonlinear operator N. Moreover, value of h is chosen as $h=1$.

Example 4

The following eighth order linear boundary value problem is considered as

$$\begin{aligned} \left. \begin{array}{l} y^{(8)}(x)+xy(x)+e^{x}(48+15x+2x^3)=0,\quad x\in {[0,1]},\\ y(0)=0,\quad y(1)=0,\\ y'(0)=1,\quad y'(1)=-e,\\ y''(0)=0,\quad y''(1)=-4e,\\ y'''(0)=-3,\quad y'''(1)=-9e.\\ \end{array} \right\} \end{aligned}$$

(15)

The analytic solution of this differential system is

$$\begin{aligned} y(x)=x(1-x)e^{x}. \end{aligned}$$

Fig. 7

Comparison of exact solution (solid line) and approximate solution (dashed line) for Example 4

Fig. 8

Absolute errors for Example 4

The initial approximation is calculated according to the standard HAM, as

$$\begin{aligned} y_{0}(x)=x-\frac{x^{3}}{2}+\frac{1}{2}x^{4}(-36+13e)+\frac{1}{2}x^{5}(84-31e)+ \frac{1}{2}x^{6}(-68+25e)+\frac{1}{2}x^{7}(19-7e). \end{aligned}$$

Using the improved adaptation proposed in the present paper, the third order approximation to the exact solution is calculated. The approximate solution values and the corresponding absolute errors are shown in Table 5.

Table 5 Numerical results for Example 4

Table 6 Comparison of maximum absolute errors

The auxiliary function H(x) is taken as $H(x)=1$. The linear operator is chosen to be the homogeneous part of the nonlinear operator N and the value of h is chosen as $h=-1$. Table 6 shows the comparison of the maximum absolute error using proposed method with that obtained by Inc and Evans [22].

Example 5

The following tenth order nonlinear boundary value problem is considered as

$$\begin{aligned} \left. \begin{array}{l} y^{(10)}(x)+e^{-x}y^{2}=e^{-x}+e^{-3x},\quad x\in {[0,1]},\\ y(0)=1,\quad y(1)=\frac{1}{e},\\ y'(0)=-1,\quad y'(1)=-\frac{1}{e},\\ y''(0)=1,\quad y''(1)=\frac{1}{e},\\ y'''(0)=-1,\quad y'''(1)=-\frac{1}{e},\\ y^{(4)}(0)=1,\quad y^{(4)}(1)=\frac{1}{e}. \end{array} \right\} \end{aligned}$$

(16)

The analytic solution of this differential system is

$$\begin{aligned} y(x)=e^{-x}. \end{aligned}$$

Fig. 9

Comparison of exact solution (solid line) and approximate solution (dashed line) for Example 5

Fig. 10

Absolute errors for Example 5

The initial approximation is calculated according to the standard HAM as

$$\begin{aligned} y_{0}(x)&= {} 1-x+\frac{x^2}{2}-\frac{x^3}{6}+\frac{x^4}{24}+\frac{(4645-1709e)x^5}{24e} \frac{(-15804+5814e)x^6}{24e}\\& \quad +\frac{(20610-7582e)x^7}{24e}+\frac{(-12148+4469e)x^8}{24e} +\frac{(2721-1001e)x^9}{24e}. \end{aligned}$$

Using the improved adaptation proposed in the present paper, the third order approximation to the exact solution is calculated.

Table 7 Comparison of absolute errors for Example 5

The auxiliary function H(x) is taken as $H(x)=1$. The linear operator is chosen to be the homogeneous part of the nonlinear operator N and the value of h is chosen as $h=-0.2$. Table 7 shows the approximate solution values and the comparison of the absolute errors using the proposed method with those obtained by Viswanadham and Ballem [31].

Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 show the comparison of the approximate solutions to the exact solutions and the variation of the absolute errors over the interval of domain for Examples 1–5.

Conclusion

In this paper, an improved adaptation of the well-known homotopy analysis method is proposed for approximate solutions of the strongly nonlinear differential equations. The method has three major advantages over the traditional homotopy analysis method. First, it involves fewer terms in each iteration. Second, the integrals involved on each iteration step are easier to manipulate. At last, it obliterates the need for extra calculations which is the main advantage over the adaptation of homotopy analysis method proposed by Odibat and Bataineh [13]. The method is illustrated with the help of different numerical examples and the results are summarized in Tables 1, 2, 3, 4, 5, 6 and 7. Tables 3, 6 and 7 show the comparison of absolute errors using the proposed method with those obtained by other methods. The comparison of the results shows that the present method is an effective tool for determining the solutions of different linear and nonlinear problems.