Introduction

In recent years, the fractional calculus used in many phenomena in engineering, physics, biology, fluid mechanics, and other sciences [1–8] can be described very successfully by models using mathematical tools from fractional calculus. Fractional derivatives provide an excellent instrument for the description of memory and hereditary properties of various materials and processes [9]. The fractional derivative has been occurring in many physical and engineering problems such as frequency-dependent damping behavior materials, signal processing and system identification, diffusion and reaction processes, creeping and relaxation for viscoelastic materials.

The new iterative method (NIM), proposed first by Gejji and Jafari [10], has proven useful for solving a variety of nonlinear equations such as algebraic equations, integral equations, ordinary and partial differential equations of integer, and fractional order and systems of equations as well. The NIM is simple to understand and easy to implement using computer packages and yield better results than the existing Adomain decomposition method [11], homotopy perturbation method [12], and variational iteration method [13].

In the present paper, we have to solve the nonlinear time-fractional Fornberg–Whitham equation by the NIM. This equation can be written in operator form as:

$$u_{t}^{\alpha } u - u_{{_{xxt} }} + u_{{_{x} }} = uu_{{_{xxx} }} - uu_{x} + 3u_{x} u_{xx} ,t > 0, 0 < \alpha \le 1$$
(1)

with the initial condition

$$u(x,0) = e^{{\frac{x}{2}}} ,$$
(2)

where u(x, t) is the fluid velocity, α is constant and lies in the interval (0, 1), t is the time and x is the spatial coordinate. Subscripts denote the partial differentiation unless stated otherwise. Fornberg and Whitham obtained a peaked solution of the form u(x, t) = Ae −1/2(|x−4t/3|) where A is an arbitrary constant.

Preliminaries and notations

In this section, we set up notation and review some basic definitions from fractional calculus [14, 15].

Definition 2.1

A real function f(x), x > 0 is said to be in space C α , α ∊ R if there exists a real number p( > α), such that f(x) = x p f 1(x) where f 1(x) ∊ C[0, ∞).

Definition 2.2

A real function f(x), x > 0 is said to be in space C m α , m ∊ IN ∪ {0} if f (m) ∊ C α .

Definition 2.3

Let f ∊ C α and α ≥ −1, then the (left-sided) Riemann–Liouville integral of order μ, μ > 0 is given by:

$$I_{t}^{\mu } f\left( {x,t} \right) = \frac{1}{\varGamma \left( \mu \right)}\int_{0}^{t} {\left( {t - \tau } \right)}^{\mu - 1} f\left( {x,\tau } \right)d\tau ,\quad \quad t > 0.$$

Definition 2.4

The (left-sided) Caputo’s fractional derivative of f, f ∊ C m-1 , m ∊ IN ∪ {0}, is defined as:

$$\begin{aligned} D_{t}^{\mu } f\left( {x,t} \right) & = \frac{{\partial^{m} }}{{\partial t^{m} }}f\left( {x,t} \right),\quad m = \mu \\ & = I_{t}^{m - \mu } \frac{{\partial^{m} f\left( {x,t} \right)}}{{\partial t^{m} }},\quad m - 1 < \mu < m,m \in IN. \\ \end{aligned}$$

Note that

$$I_{t}^{\mu } D_{t}^{\mu } f\left( {x,t} \right) = f\left( {x,t} \right) - \sum\limits_{k = 0}^{m - 1} {\frac{{\partial^{k} }}{{\partial t^{k} }}} f\left( {x,0} \right)\frac{{t^{k} }}{k!},\quad m - 1 < \mu < m,m \in IN.$$
$$I_{t}^{\mu } t^{v} = \frac{{\varGamma \left( {v + 1} \right)}}{{\varGamma \left( {\mu + v + 1} \right)}}t^{v + \mu } .$$

Basic idea of new iterative method (NIM)

To describe the idea of the NIM, consider the following general functional equation [10, 16–20]:

$$u(x) = f(x) + N(u(x)),$$
(3)

where N is a nonlinear operator from a Banach space B → B and f is a known function. We are looking for a solution u of (3) having the series form:

$$u(x) = \sum\limits_{i = 0}^{\infty } {u_{i} (x)} .$$
(4)

The nonlinear operator N can be decomposed as follows:

$$N\left( {\sum\limits_{i = 0}^{\infty } {u_{i} } } \right) = N(u_{0} ) + \sum\limits_{i = 1}^{\infty } {\left\{ {N\left( {\sum\limits_{j = 0}^{i} {u_{j} } } \right) - N\left( {\sum\limits_{j = 0}^{i - 1} {u_{j} } } \right)} \right\}} .$$
(5)

From Eqs. (4) and (5), Eq. (3) is equivalent to:

$$\sum\limits_{i = 0}^{\infty } {u_{i} } = f + N(u_{0} ) + \sum\limits_{i = 1}^{\infty } {\left\{ {N\left( {\sum\limits_{j = 0}^{i} {u_{j} } } \right) - N\left( {\sum\limits_{j = 0}^{i - 1} {u_{j} } } \right)} \right\}} .$$
(6)

We define the recurrence relation:

$$u_{0} = f,$$
(7a)
$$u_{1} = N(u_{0} ),$$
(7b)
$$u_{n + 1} = N(u_{0} + u_{1} + \cdots + u_{n} ) - N(u_{0} + u_{1} + \cdots + u_{n - 1} ),\,\,\,\,\,\,\,\,n = 1,2,3, \ldots .$$
(7c)

Then:

$$\begin{aligned} (u_{1} + \cdots + u_{n + 1} ) & = N(u_{0} + u_{1} + \cdots + u_{n} )\,,\,\,\,\,\,\,\,\,\,n = 1,2,3, \ldots , \\ & u = \sum\limits_{i = 0}^{\infty } {u_{i} } = f + N\left( {\sum\limits_{i = 0}^{\infty } {u_{i} } } \right) \\ \end{aligned}$$
(8)

If N is a contraction, i.e.,

$$\left\| {N(x) - N(y)} \right\| \le k\left\| {x - y} \right\|, \quad 0 < k < 1,$$

then:

$$\begin{aligned} \left\| {u_{n + 1} } \right\| & = \left\| {N(u_{0} + u_{1} + \cdots + u_{n} ) - N(u_{0} + u_{1} + \cdots + u_{n - 1} )} \right\| \\ & \le k\left\| {u_{n} } \right\| \le \cdots \le k^{n} \left\| {u_{0} } \right\|\;n = 0, 1, 2, \ldots , \\ \end{aligned}$$
(9)

and the series ∑  ∞ i=0 u i absolutely and uniformly converges to a solution of (3) [21], which is unique, in view of the Banach fixed point theorem [22]. The k term approximate solution of (3) and (4) is given by ∑  k−1 i=0 u i .

Convergence analysis of the new iterative method (NIM)

Now, we introduce the condition of convergence of the NIM, which is proposed by Daftardar-Gejji and Jafari in (2006) [10], also called (DJM) [23].

From (5), the nonlinear operator N is decomposed as follows:

N(u) = N(u 0) + [N(u 0 + u 1) − N(u 0)] + [N(u 0 + u 1 + u 2) − N(u 0 + u 1)] + ….

Let G 0 = N(u 0) and

$$G_{n} = N\left( {\sum\limits_{i = 0}^{n} {u_{i} } } \right) - N\left( {\sum\limits_{i = 0}^{n - 1} {u_{i} } } \right),\,\,\,\,\,\,\,\,\,n = 1,2,3, \ldots .$$
(10)

Then N(u) = ∑  ∞ i=0 G i .

Set:

$$u_{0} = f,$$
(11)
$$u_{n} = G_{n - 1} ,\,\,\,\,\,n = 1,2,3, \ldots .$$
(12)

Then:

$$u = \sum\limits_{i = 0}^{\infty } {u_{i} }$$
(13)

is a solution of the general functional Eq. (3). Also, the recurrence relation (7) becomes

$$\begin{aligned} u_{0} & = f, \\ u_{n} & = G_{n - 1} ,\quad n = 1,2, \ldots . \\ \end{aligned}$$
(14)

Using Taylor series expansion for G i , i = 1, 2, …, n, we have

$$\begin{aligned} G_{1} & = N(u_{0} + u_{1} ) - N(u_{0} ) \\ & = N(u_{0} ) + N^{\prime}(u_{0} )u_{1} + N^{\prime\prime}(u_{0} )\frac{{u_{1}^{2} }}{2!} + \cdots - N(u_{0} ) \\ & = \sum\limits_{k = 1}^{\infty } {N^{k} } (u_{0} )\frac{{u_{1}^{k} }}{k!}, \\ \end{aligned}$$
(15)
$$\begin{aligned} G_{2} & = N(u_{0} + u_{1} + u_{2} ) - N(u_{0} + u_{1} ) \\ & = N^{\prime}(u_{0} + u_{1} )u_{2} + N^{\prime\prime}(u_{0} + u_{1} )\frac{{u_{2}^{2} }}{2!} + \cdots \\ & = \sum\limits_{j = 1}^{\infty } {\left[ {\sum\limits_{i = 0}^{\infty } {N^{(i + j)} } (u_{0} )\frac{{u_{1}^{i} }}{i!}} \right]} \frac{{u_{2}^{j} }}{j!} \\ \end{aligned}$$
(16)
$$G_{3} = \sum\limits_{{i_{3} = 1}}^{\infty } {\sum\limits_{{i_{2} = 0}}^{\infty } {\sum\limits_{{i_{1} = 0}}^{\infty } {N^{{(i_{1} + i_{2} + i_{3} )}} } (u_{0} )\frac{{u_{3}^{{i_{3} }} }}{{i_{3} !}}} } \frac{{u_{2}^{{i_{2} }} }}{{i_{2} !}}\frac{{u_{1}^{{i_{1} }} }}{{i_{1} !}}.$$
(17)

In general:

$$G_{n} = \sum\limits_{{i_{n} = 1}}^{\infty } {\sum\limits_{{i_{n - 1} = 0}}^{\infty } { \cdots \sum\limits_{{i_{1} = 0}}^{\infty } {\left[ {N^{{(\sum\limits_{k = 1}^{n} {i_{k} } )}} (u_{0} )\left( {\prod\limits_{j = 1}^{n} {\frac{{u_{j}^{{i_{j} }} }}{{i_{j} !}}} } \right)} \right]} } } .$$
(18)

In the following theorem, we state and prove the condition of convergence of the method.

Theorem 3.1

If N is C (∞) in a neighborhood of u 0 and

$$\left\| {N^{(n)} (u_{0} )} \right\| = \sup \left\{ {N^{(n)} (u_{0} )(h_{1} , \ldots ,h_{n} ):\left\| {h_{i} } \right\| \le 1,\,\,\,1 \le i \le n} \right\} \le L,$$
(19)

for any n and for some real L > 0 and \(\left\| {u_{i} } \right\| \le M < \frac{1}{e}\,,\,\,i = 1,2, \ldots ,\) then the series ∑  ∞ n=0 G n is absolutely convergent, and moreover,

$$\left\| {G_{n} } \right\| \le LM^{n} e^{n - 1} (e - 1),\,\,n = 1,2, \ldots .$$
(20)

Proof

In view of (18)

$$\left\| {G_{n} } \right\| \le LM^{n} \sum\limits_{{i_{n} = 1}}^{\infty } {\sum\limits_{{i_{n - 1} = 0}}^{\infty } { \cdots \sum\limits_{{i_{1} = 0}}^{\infty } {\left[ {\left( {\prod\limits_{j = 1}^{n} {\frac{{u_{j}^{{i_{j} }} }}{{i_{j} !}}} } \right)} \right]} } } = LM^{n} e^{n - 1} (e - 1).$$
(21)

\(\square\)

Thus, the series ∑  ∞ n=1 ‖G n ‖ is dominated by the convergent series LM(e − 1) ∑  ∞ n=1 (Me)n−1, where \(M < \frac{1}{e}\). Hence, ∑  ∞ n=0 G n is absolutely convergent, due to the comparison test. For more details, see [23].

Reliable algorithm of new iterative method (NIM) for solving the Linear and Nonlinear fractional partial differential equations

After the above presentation of the NIM, we introduce a reliable algorithm for solving nonlinear fractional PDEs using the NIM. Consider the following nonlinear fractional PDE of arbitrary order:

$$D_{t}^{\alpha } u(x,t) = A(u,\partial u) + B(x,t),\,\,\,\,\,\,\,\,\,m - 1 < \alpha \le m,\,m \in IN$$
(22)

with the initial conditions

$$\frac{{\partial^{k} }}{{\partial t^{k} }}u(x,0) = h_{k} (x),\quad k = 0,1,2, \ldots ,m - 1,$$
(23)

where A is a nonlinear function of u and ∂u (partial derivatives of u with respect to x and t) and B is the source function. In view of the integral operators, the initial value problem (22) is equivalent to the following integral equation

$$u(x,t) = \sum\limits_{k = 0}^{m - 1} {h_{k} (x)\frac{{t^{k} }}{k!} + I_{t}^{\alpha } B(x,t) + I_{t}^{\alpha } A = f + N(u)} ,$$
(24)

where

$$f = \sum\limits_{k = 0}^{m - 1} {h_{k} (x)\frac{{t^{k} }}{k!} + I_{t}^{\alpha } B(x,t)} ,$$
(25)

and

$$N(u) = I_{t}^{\alpha } A,$$
(26)

where I n t is an integral operator of n fold. We get the solution of (24) by employing the algorithm (7).

Solution of the problem

We first consider the following time-fractional Fornberg–Whitham equation [24, 25]:

$$D_{t}^{\alpha } u - D_{{_{xxt} }} u + D_{{_{x} }} u = uD_{{_{xxx} }} u - uD_{x} u + 3D_{x} uD_{xx} u ,$$
(27)

with the initial condition:

$$u(x,0) = e^{{\frac{x}{2}}} .$$
(28)

Then, the exact solution is given by:

$$u(x,t) = e^{{\frac{x}{2}\, - \,\frac{2t}{3}}} .$$
(29)

Note that Eq. (27) is equivalent to the integral equation

$$u\left( {x,t} \right) = e^{{\frac{x}{2}}} + I_{t}^{\alpha } \left[ {D_{t}^{\alpha } u - D_{{_{xxt} }} u + D_{{_{x} }} u + uD_{{_{xxx} }} u - uD_{x} u + 3D_{x} uD_{xx} u} \right],$$

where \(f = e^{{\frac{x}{2}}}\) and \(N(u) = I_{t}^{\alpha } \left[ {D_{t}^{\alpha } u - D_{{_{xxt} }} u + D_{{_{x} }} u + uD_{{_{xxx} }} u - uD_{x} u + 3D_{x} uD_{xx} u} \right]\), using (7) we get

$$u_{0} (x,t) = e^{{\frac{x}{2}}} ,$$
$$u_{1} (x,t) = - \frac{1}{2}e^{{\frac{x}{2}}} \frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}},$$
$$u_{2} (x,t) = - \frac{1}{8}e^{{\frac{x}{2}}} \frac{{t^{2\alpha - 1} }}{{\varGamma \left( {2\alpha } \right)}} + \frac{1}{2}e^{{\frac{x}{2}}} \frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}},$$
$$u_{3} (x,t) = - \frac{1}{32}e^{{\frac{x}{2}}} \frac{{t^{3\alpha - 2} }}{{\varGamma \left( {3\alpha - 1} \right)}} + \frac{1}{8}e^{{\frac{x}{2}}} \frac{{t^{3\alpha - 1} }}{{\varGamma \left( {3\alpha } \right)}} - \frac{1}{8}e^{{\frac{x}{2}}} \frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}},$$
$$\vdots$$

Therefore, the NIM series solution is:

$$u(x,t) = e^{{\frac{x}{2}}} \left( {1 - \frac{{t^{\alpha } }}{{2\varGamma \left( {\alpha + 1} \right)}} - \frac{{t^{2\alpha - 1} }}{{8\varGamma \left( {2\alpha } \right)}} + \frac{{t^{2\alpha } }}{{2\varGamma \left( {2\alpha + 1} \right)}} - \frac{{t^{3\alpha - 2} }}{{32\varGamma \left( {3\alpha - 1} \right)}} + \frac{{t^{3\alpha - 1} }}{{8\varGamma \left( {3\alpha } \right)}} - \frac{{t^{3\alpha } }}{{8\varGamma \left( {3\alpha + 1} \right)}} + \cdots } \right)$$
(30)

Numerical results and discussion

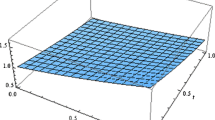
In this section, we calculate numerical results of the displacement u(x, t) for different time-fractional Brownian motions α = 2/3, 3/4, 1 and for various values of t and x. The numerical results for the approximate solution (30) obtained using NIM and the exact solution for various values of t, x, and a are shown by Figs. 1, 2, 3, 4 and those for different values of t and α at x = 1 are depicted in Fig. 5. It is observed from Figs. 1, 2, 3, 4 that u(x, t) increases with the increase in both x and t for α = 2/3, 3/4 and α = 1. Figure 4 clearly show that, when α = 1, the approximate solution (30) obtained by the present method is very near to the exact solution. It is also seen from Fig. 5 that as the value of a increases, the displacement u(x, t) increases but afterward its nature is opposite. Finally, we remark that the approximate solution (30) is in full agreement with the results obtained homotopy perturbation method [24] and homotopy perturbation transform method [25]. In Table 1, we compute the absolute errors for differences between the exact solution (29) and the approximate solution (30) obtained by the NIM at some points.

Fig. 1
figure 1

The surfaces show the approximate solutions u 5(x, t) for α = 2/3

Full size image
Fig. 2
figure 2

The surfaces show the approximate solutions u 5(x, t) for α = 3/4

Full size image
Fig. 3
figure 3

The surfaces show the approximate solutions u 5(x, t) for α = 1

Full size image
Fig. 4
figure 4

The surfaces show the exact solution of u(x, t)

Full size image
Fig. 5
figure 5

Plots of u(x, t) at x = 1 for different values of α

Full size image
Table 1 The absolute errors for differences between the exact solution and 5th-order NIM when α = 1
Full size table

Conclusion

In this paper, the new iterative method (NIM) has been applied for approximating the solution for the nonlinear fractional Fornberg–Whitham equation. The accuracy of the NIM for solving nonlinear fractional Fornberg–Whitham equation is good compared to the literature; however, it has the advantage of reducing the computations complexity presented in other perturbation techniques. In fact, in NIM, nonlinear problems are solved without using Adomian’s polynomials or He’s polynomials that appear in the decomposition methods. The numerical results show that the proposed method is reliable and efficient technique in finding approximate solutions for nonlinear differential equations.