Abstract
The current work highlights the following issues: a brief survey of the development in the theory of fractional differential equations has been raised. A very recent technique based on the generalized Taylor series called—residual power series (RPS)—is introduced in detailed manner. The time-fractional foam drainage equation is considered as a target model to test the validity of the RPS method. Analysis of the obtained approximate solution of the fractional foam model reveals that RPS is an alternative method to be added for the fractional theory and computations and considered to be a significant method for exploring nonlinear fractional models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The last four decades witness fundamental works and developments on the fractional derivative and fractional differential equations. Oldham and Spanier [1], Miller and Ross [2], Samko et al. [3], Podlubny [4], Kilbas et al. [5] and others [6, 7] are the pioneer in this field; their works form an introduction to the theory of fractional differential equations and provide a systematic understanding of the fractional calculus such as the existence and the uniqueness of solutions. Hernandez et al. [8] published a paper on recent developments in the theory of abstract differential equations with fractional derivative. Finally, interested various applications of fractional calculus in the field of interdisciplinary sciences such as image processing and control theory have been studied by Magin et al. [9] and Mainardi [10].
In the literature, there exist no methods that produce an exact solution for nonlinear fractional differential equations. Only approximate solutions can be derived using linearization or successive or perturbation methods. Such methods are: variational iteration method and multivariate Pade approximations [11], Iterative Laplace transform method [12], Adomian decomposition method [13–17], Homotopy analysis method [18, 19] and Sumudu transform method [20].
The main objective of this paper is to conduct a new novel technique called residual power series method to study the solution of time-fractional Foam drainage model described by
subject to the initial conditions:
It is a simple model of the flow of liquid through channels (Plateau borders) and nodes (intersection of four channels) between the bubbles, driven by gravity and capillarity [21, 22]. Approximate solutions of Eqs. (1.1)–(1.2) have been obtained by different methods; Adomian decomposition method [23], the Homotopy analysis method [24] and the variational iteration method [25]. It should be noted here that none of the previous studies addressed the accuracy of such methods.
The pattern of the current paper is as follows: In Sect. 2, some definitions and theorems regarding Caputo’s derivative and fractional power series are given. In Sect. 3, we derive a residual power series solution to the time-fractional foam drainage equation. Graphical results regarding the foam drainage model are presented in Sect. 4.
Preliminaries
Many definitions and studies of fractional calculus have been proposed in the literature. These definitions include: Grunwald–Letnikov, Riemann–Liouville, Weyl, Riesz and Caputo sense. In the Caputo case, the derivative of a constant is zero and one can define, properly, the initial conditions for the fractional differential equations which can be handled using an analogy with the classical integer case. For these reasons, researchers prefer to use the Caputo fractional derivative [26] which is defined as
Definition 2.1
For \(m\) to be the smallest integer that exceeds \(\alpha \), the Caputo fractional derivatives of order \(\alpha >0\) are defined as
Now, we survey some needed definitions and theorems regarding the fractional power series (RPS) where there is much theory to be found in [27, 28].
Definition 2.2
A power series expansion of the form
is called fractional power series PS about \(t=t_0\)
Theorem 2.1
Suppose that \(f\) has a fractional PS representation at \(t=t_0\) of the form
If \(D^{m\alpha } f(t),\ \ m=0,1,2,\ldots \) are continuous on \((t_0, t_0+R)\) , then \(c_m=\frac{D^{m\alpha } f(t_0)}{\Gamma (1+m\alpha )}.\)
Definition 2.3
A power series expansion of the form
is called multiple fractional power series PS about \(t=t_0\)
Theorem 2.2
Suppose that \(u(x,t)\) has a multiple fractional PS representation at \(t=t_0\) of the form
If \(D_t^{m\alpha } u(x,t),\quad m=0,1,2,\ldots \) are continuous on \(I\times (t_0, t_0+R)\) , then \(f_m(x)=\frac{D_t^{m\alpha } u(x,t_0)}{\Gamma (1+ m\alpha )}.\)
From the last theorem, it is clear that if \(n+1\)-dimensional function has a multiple fractional PS representation at \(t=t_0\), then it can be derived in the same manner, i.e.
Corollary 2.3
Suppose that \(u(x,y,t)\) has a multiple fractional PS representation at \(t=t_0\) of the form
If \(D_t^{m\alpha } u(x,y,t),\ \ m=0,1,2,\ldots \) are continuous on \(I_1\times I_2 \times (t_0, t_0+R)\) , then \(g_m(x,y)=\frac{D_t^{m\alpha } u(x,y,t_0)}{\Gamma (1+ m\alpha )}.\)
Next, we present in details the derivation of the residual power series solution to the generalized fractional DSW system.
Residual power series (RPS) of the foam drainage model
The aim of this section is to construct power series solution to the time-fractional Foam drainage model by substituting its power series (PS) expansion among its truncated residual function [29, 30]. From the resulting equation, a recursion formula for the computation of the coefficients is derived, while the coefficients in the fractional PS expansion can be computed recursively by recurrent fractional differentiation of the truncated residual function.
The RPS method proposes the solution for Eqs. (1.1–1.2) as a fractional PS about the initial point \(t=0\)
Next, we let \(u_k(x,t)\) to denote the k-th truncated series of \(u(x,t)\), i.e.,
It is clear that by condition (1.2) the \(0\)-th RPS approximate solutions of \(u(x,t)\) is
Also, Eq. (3.2) can be written as
Now, we define the residual functions, \(Res\), for Eq. (1.1)
and, therefore, the \(k\)-th residual function, \(Res_{u,k}\), is
As in [29, 30], \(Res(x,t)=0\) and \(\lim _{k\rightarrow \infty }Res_k(x,t)=Res(x,t)\) for all \(x\in I\) and \(t\ge 0\). Therefore, \(D_t^{r\alpha }Res(x,t)=0\) since the fractional derivative of a constant in the Caputo’s sense is \(0\). Also, the fractional derivative \(D_t^{r\alpha }\) of \(Res(x,t)\) and \(Res_k(x,t)\) is matching at \(t=0\) for each \(r=0,1,2,\ldots ,k\).
To clarify the RPS technique, we substitute the \(k\)-th truncated series of \(u(x,t)\) into Eq. (3.6), find the fractional derivative formula \(D_t^{(k-1)\alpha }\) of both \(Res_{u,k}(x,t),\ \ k=1,2,3,\ldots ,\) and then solve the obtained algebraic system
to get the required coefficients \(f_n(x),\ \ n=1,2,3,\ldots ,k\) in Eq. (3.4). Now, we follow the following steps.
Step 1. To determine \(f_1(x)\), we consider \((k=1)\) in (3.6)
But, \(u_1(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}\). Therefore,
From Eq. (3.7), we deduce that \(Res_{u,1}(x,0)=0\) and thus,
Therefore, the \(1\)st RPS approximate solution is
Step 2. To obtain \(f_2(x)\), we substitute the \(2\)nd truncated series \(u_2(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}+f_2(x) \frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\) into the \(2\)nd residual function \(Res_{u,2}(x,t)\), i.e.,
Applying \(D_t^{\alpha }\) on both sides of Eq. (3.12) gives
By the fact that \(D_t^{\alpha }Res_{u,2}(x,0)=0\) and solving the resulting system in (3.13) for the unknown coefficient function \(f_2(x)\), we get
Step 3. We derive the formula of the coefficient function \(f_3(x)\). Substitute the \(3\)rd truncated series \(u_3(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}+f_2(x) \frac{t^{2\alpha }}{\Gamma (1+2\alpha )}+f_3(x) \frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\) into the \(3\)rd residual function \(Res_{u,3}(x,t)\). i.e.,
Now, we apply the operator \(D_t^{2\alpha }\) on both sides of Eq. (3.15)
Thus, solving the equation \(D_t^{2\alpha }Res_{u,3}(x,0)=0\) results in the following recurrence formula
Finally, we follow the same manner as above and solve the equation \(D_t^{3\alpha }Res_{u,4}(x,0)=0\) to deduce the following result
By the above recurrence relations, we are ready to present some graphical results regarding the time-fractional Foam drainage model.
Applications and results
The purpose of this section is to test the derivation of residual power series solutions of the following time-fractional foam drainage equation.
subject to the initial conditions:
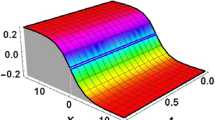
Where the exact solution of this model when \(\alpha =1\) is \(u(x,t)=-\sqrt{c}\tanh (\sqrt{c} (x-ct))\). Based on the obtained results from the previous section, we consider only the \(4{th}\) RPS approximate solution. Figure 1 represents the \(4\)th RPS approximate solution of the function \(u(x,t)\) for different values of the fractional derivative \(\alpha \). To validate the efficiency and accuracy of the analytical scheme, we give explicit values of \(x\) and \(t\) and compute the absolute error compared with the exact solution when \(\alpha =1\) (See Table 1). Figure 2 represents solutions to the fractional foam drainage when the initial condition is \(f(x)=x\) for \(\alpha =0.5,\ 1\). Finally, Fig. 3 represents solutions to the fractional foam drainage when the initial condition is \(f(x)=\sin (x)\) for \(\alpha =0.5,\ 0.75,\ 1\).
In the theory of fractional calculus, it is obvious that when the fractional derivative \(n-1<\alpha < n\) tends to positive integer \(n\), the approximate solution continuously tends to the exact solution of the problem with derivative \(n=1\). It is also clear from Figs. 1, 2 and 3 that when \(\alpha \) is close to 0, the solutions bifurcate and provide wave-like pattern. But, when \(\alpha \) is close to 1, there is no pattern.
Conclusions
A new analytical iterative technique based on the residual power series is proposed to obtain an approximate solution to a nonlinear time-fractional foam drainage equation. Three different initial conditions of the Foam model are considered and accordingly different physical behaviors are produced. We observed when \(\alpha \) is close to 0, the solutions bifurcate and provide wave-like pattern. But, when \(\alpha \) is close to 1, there is no pattern (Figs. 1 and 3). This bifurcation phenomenon will help the researchers to open many new avenues to better understanding of time-fractional derivatives and its relation to real-life phenomena. The accuracy of the proposed method has been tested by studying the absolute errors of the obtained approximate of the Foam model (Table 1). The RPS method is a promising technique based on its simplicity and accuracy. It is to be considered an additive tool for the field of fractional theory and computations. As future work, we will extend the RPS method to handle (\(2+1\))-dimensional linear and nonlinear space- and time-fractional physical models.
References
Oldham, K.B., Spanier, J.: The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary order. Academic Press, California (1974)
Miller, K., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Ray, S.S.: Analytical solution for the space fractional diffusion equation by two-step Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul. 14, 1130–1295 (2009)
Podlubny, I.: Fractional Differential Equations. Academic Press, California (1999)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amstrdam (2006)
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, New York (2010)
Caponetto, R., Dongola, G., Fortuna, L., Petras, I.: Fractional Order Systems: Modeling and Control Applications. World Scientific Publishing Company, Singapore (2010)
Hernandez, E., O’Regan, D., Balachandran, K.: On recent developments in the theory of abstract differential equations with fractional derivatives. Nonlinear Anal.: Theory Methods Appl. 73, 3462–3471 (2010)
Magin, R., Ortigueira, M.D., Podlubny, I., Trujillo, J.J.: On the fractional signals and systems. Signal Process. 91, 350–371 (2011)
Mainardi, F.: Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Imperial College Press, London (2010)
Turut, V., Guzel, N.: On solving partial differential equations of fractional order by using the variational iteration method and multivariate Pad approximations. Eur. J. Pure Appl. Math. 6(2), 147–171 (2013)
Jafaria, J., Nazarib, M., Baleanuc, D., Khalique, C.M.: A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 66(5), 838–843 (2013)
Al-khaled, K., Momani, S.: An approximate solution for a fractional diffusion-wave equation using the decomposition method. Appl. Math. Comput. 165(2), 473–483 (2005)
Wang, Q.: Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method. Appl. Math. Comput. 182, 1048–1055 (2006)
Hu, Y., Luo, Y., Lu, Z.: Analytical solution of the linear fractional differential equation by Adomian decomposition method. J. Comput. Appl. Math. 215, 220–229 (2008)
Parthiban, V., Balachandran, K.: Solutions of system of fractional partial differential equations. Appl. Appl. Math. 8(1), 289–304 (2013)
Al-khaled, K., Alquran, M.: An approximate solution for a fractional model of generalized Harry Dym equation. Math Sci (2015). doi:10.1007/s40096-015-0137-x
Dehghan, M., Manafian, J., Saadatmandi, A.: Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial Differ. Equ. 26(2), 448–479 (2010)
Ganjiani, M.: Solution of nonlinear fractional differential equations using Homotopy analysis method. Appl. Math. Model. 34(6), 1634–1641 (2010)
K. Al-Khaled, Numerical solution of time-fractional partial differential equations using Sumudu Decomposition method. Rom. J. Phys. 60(1–2) (2015)
Verbist, G., Weuire, D., Kraynik, A.M.: The foam drainage equation. J. Phys. Condens. Matter 8, 3715–3731 (1996)
Weaire, D., Hutzler, S., Cox, S., Alonso, M.D., Drenckhan, D.: The fluid dynamics of foams. J. Phys. Condens. Matter 15, S65–S73 (2003)
Dahmani, Z., Mesmoudi, M.M., Bebbouch, R.: The Foam Drainage equation with time- and space-fractional derivatives solved by the Adomian method. Electron. J. Qual. Theory Differ. Equ. 30, 1–10 (2008)
Fadravi, H.H., Nik, H.S., Buzhabadi, R.: Homotopy analysis method for solving Foam Drainage equation with space- and time-fractional derivatives. Int. J. Differ. Equ. (2011) (Article ID 237045)
Dahmani, Zoubir, Anber, Ahmed: The variational iteration method for solving the fractional foam drainage equation. Int. J. Nonlinear Sci. 10(1), 39–45 (2010)
Gomez-Aguilar, J.F., Razo-Hernandez, R., Granados-Lieberman, D.: A physical interpretation of fractional calculus in observables terms: analysis of the fractional time constant and the transitory response. Revista Mexicana de Fisica 60, 32–38 (2014)
El-Ajou, A., Arqub, O.A., Momani, S.: Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: a new iterative algorithm. J. Comput. Phys. (2014) (In press)
El-Ajou, A., Abu, O., Al Zhour, Z.A., Momani, S.: New results on fractional power series: theories and applications. Entropy 15, 5305–5323 (2013)
Arqub, O.A.: Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 5, 31–52 (2013)
Arqub, O.A., El-Ajou, A., Bataineh, A., Hashim, I.: A representation of the exact solution of generalized Lane Emden equations using a new analytical method. Abstr. Appl. Anal. (2013) (Article ID 378593)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Alquran, M. Analytical solutions of fractional foam drainage equation by residual power series method. Math Sci 8, 153–160 (2014). https://doi.org/10.1007/s40096-015-0141-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-015-0141-1