Abstract
This study proposes a design model for conserving and utilizing energy affordably and intermittently considering the wind rush experienced in the patronage of renewable energy sources for cheaper generation of electricity and the solar energy potential especially in continents of Africa and Asia. Essentially, the global quest for sustainable development across every sector is on the rise; hence, the need for a sustainable method of extracting energy cheaply with less wastage and pollution is on the priority list. This research, integrates and formulates different ideologies, factors and variables that have been adopted in previous research studies to create an efficient system. Some of the aforementioned researches includes pumped hydro gravity storage system, Compressed air gravity storage system, suspended weight in abandoned mine shaft, dynamic modelling of gravity energy storage coupled with a PV energy plant and deep ocean gravity energy storage. As an alternative and a modification to these systems, this research is proposing a Combined solar and gravity energy storage system. The design synthesis and computational modelling of the proposed system model were investigated using a constant height and but varying mass. Efficiencies reaching up to 62% was achieved using the chosen design experimental parameters adopted in this work. However, this efficiency can be tremendously improved upon if the design parameters are modified putting certain key factors which are highlighted in the limitation aspect of this research into consideration. Also, it was observed that for a test load of 50 × 103 mA running for 10 h (3600 s), the proposed system will only need to provide a torque of 3.27Nm and a height range of 66.1 × 104 m when a mass of 10 kg is lifted to give out power of 48 kwh. Since gravity storage requires intermittent actions and structured motions, mathematical models were used to analyse the system performance characteristics amongst other important parameters using tools like MATLAB Simscape modelling toolbox, Microsoft excel and Sysml Model software.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
Introduction
Renewable energy of any form has been observed over time to have high investment costs and therefore necessitate its operation where its resource is readily available.
However, the major problem after producing the energy is finding the most economical way of storing it due to the its variable nature that most often do not match demand patterns. Solar energy, a promising renewable energy, has a rich capacity of about 23,000 TW per year and could fully satisfy global energy consumption (around 16 TW per year) [1, 2]. Effectively, its attractive characteristics of no pollution and low operation cost provides it with great practical application. Nevertheless, the nature of usage (intermittency) inherently affects its extensive applications and this performance specification is also one complicated characteristics of other forms of renewable energy as continuous delivery of energy is not assured due to some natural and operational alterations. Hence, it is now very imperative to come up with designs for energy conversion / storage systems that would offset the alterations after production in order to match variable supply with varying demand from users. Hence, the need for a buffer to utilize judiciously the excess energy in favourable days (days of intense sunlight). This has consequently led to the rapid development of cheap, efficient and reliable storage technologies that will aid full maximization of renewable energy potential and substantial eradication of fossil fuels utilization particularly in temperate regions like Africa.
Nowadays, energy production sources are expected to be reduced in cost, increased in reliability and have little or no carbon emission. The global environmental concerns and recent 2016 agreement in Paris have led to strict monitoring on greenhouse gases emission and impact on the environment [3]. These concerns on climate change have consequently driven the focus of energy systems towards renewable sustainable energy sources and countless number of literatures have suggested that tilting dependability towards these renewable resources might boost the availability of energy globally. But it tends to be less reliable and cost intensive compared to other generating methods that rely on fuels. Reliability on a broader scale in terms of meeting load demands and assuring efficiency, investigates four aspect any renewable energy system which include; energy storage system, auxiliary backup, geographical diversification and resource diversification. In this research, the attention will be geared towards the Energy storage system which is the most expensive part. Hence this research aims to design an integrated solar energy storage system utilizing the potential of gravity using a suspended mass. This will be achieved by using a Solar PV cell, bulk booster charge controller, Inverter unit, Solenoid device, deep cycle battery, pulley block, geared motor, a microcontroller(Arduino) and wire ropes.
The utilization of the gravity to store energy of any form is an idea in its infant stage [4]. Study shows that the pumped hydroelectric storage system (PHES) still remains the current most harnessed form of storage in the world on a long term and on a large scale [5]. Along the years, a lot of variations have been seen in the traditional layout of the pumped hydroelectric storage (PHES) but much recently, several works have been done on dry (i.e. Waterless) forms of gravity storage.
Pumped hydroelectricity accounts for more than 99% of the world’s large-scale energy storage making it the most utilized method worldwide [5]. In most cases, the system comprises of two dams or reservoirs such that one is higher and the other is lower to enable the system store potential energy by virtue of the water stored in the higher reservoir. This potential energy is harnessed when water is released from the higher reservoir via a turbine to the lower reservoir thus generating energy. Although the numerous advantages associated with this system which include large storage capacity, high efficiency between 65 and 87% and scalability, it still poses some obvious draw backs. The energy density of the system is low since the gravity on the earth surface is relatively weak; hence, a large reservoir capacity or large height variation will be required to store qualitative amount of energy [4, 6]. Also, site selection criteria are a major consideration.
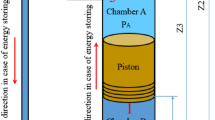
A typical hydro system that rely on gravity to store energy is the dynamic modelling of gravity energy storage coupled with a PV energy plant work by Asmae Berrada et al. The aim of his model is to investigate gravity effect on energy storage. The system basically comprises of a large piston, a container filled with water, a return pipeline and a mechanical device to release and store energy. The efficiency of this system is estimated to be more than 80% and considered to be a comparative design to generate large megawatt of power [7, 8]. The gravity power module (GPM) is a similar storage system to the piston based pumped hydroelectric system developed by Asmae Berrada et al., but it utilizes a much larger piston. This system provides power and energy in the range of 40 MW/160MWH to 1.6GW/6.4GWH [8].
Similarly, the compressed air gravity storage is also an improved modification of Pumped hydro gravity energy storage technology. It is a combination of the concept of gravity storage and compressed air. This is actually an interesting way to increase the water pressure. Here, a pressure vessel with an air compressor pot was included to the normal gravity storage components to form this system. High atmospheric pressure corresponds to an increasing Pump hydro storage (PHS) height difference. For example, adding 2 mpa to atmospheric pressure equals raising water by 200 m. In this way, the energy is stored in the compressed air and released in the stored mode when discharging. This gravitational storage of compressed air solves some of the problems encountered by bulk energy storage.
This system is economically efficient in the sense that it does not require fossil fuels or special regulations (difference in height) unlike the pumped gravity hydro [9]. In addition, it does not use the expansion of gas turbines and air turbines. However, it is constrained by limited availability of natural reservoirs located underground and, in its efficiency, compared to battery. Furthermore, in compression of air, there tend to be a rapid increase in the temperature of air, hence, a part of the energy stored during the process is lost in the attempt to realize a reversible cycle process system.
In like manner, the gravitricity system by Charles Blair which is believed to possess enormous potential economic benefits. It is projected to produce about 10mwh amount of power if used on one of the deepest mines in the UK of about 3000feet (about 1250 m) [10, 11]. Basically, the system includes a renewable energy source (Wind energy in this case), a suspended weight, sets of pulleys (about four) and electric grid network [12]. Admittedly, the gravitricity idea looks very much like the proposed idea in this paper but its major drawbacks stems from limited individual system capacity, availability of data on abandoned shaft locations around a geographical location (for example in a country). Also, depths and diameter data parameters of random mine shaft discovered poses another challenge as it will be a rigorous task in estimating how many shafts might be amenable to development or redesign [13].
Pedretti et al. in his work made use of crane platform with a winch to lift blocks of concrete from the ground to a certain height and arranged in a stack of concrete blocks [14]. During low demand periods, the crane carries out the lifting and arranging sequence to store energy. The system is said to be “fully charged” when the crane has created a tower of concrete blocks around itself to a predetermined height. Then, during high energy demand period, the reverse takes place. However, the main challenges in this work has been figuring out how to automate relevant operations, like hooking and unhooking concrete blocks, and to counteract the pendulum like movement of the blocks when being lifted or lowered [10]. Also, the mathematical complexity in figuring out a precise algorithm to ensure the placing of one concrete block on other places a huge demand on the design requirement of this system (Fig. 1).
Furthermore, Thomas Morstyn et al., developed the design of Gravity energy storage using suspended weights for abandoned mine shafts. Energy is stored in this system by delivering current from the electrical network to raise the suspended weights along the rail set up in the system. The main components of this system include mine shaft, suspended weight, an induction motor connected to the weights by ropes and an active inverter (front end) designed to provide bidirectional interface between the electrical network set up and electric motor.
The power delivered from the electric motor is proportional to the speed and mass of the suspended weight. In effect, additional power is required to attain higher rates of acceleration and this will consequently require higher capacity motors and power electronics to provide high ramp rates (e.g. 1 s frequency response) needed by the power system services [15, 16]. In this system, power is supplied to the grid by the principle of regenerative braking applied in most cranes by releasing the mass (suspended weight) and recovering the energy stored. The electrical network side requires an active front end inverter and AC mains connected to a bi-directional active front end rectifier. In effect, a DC capacitor is used in the set up to provide an interface between the rectifier and a voltage source rectifier that supplies power to the motor. Essentially, the bi- directional rectifier is manipulated in this system to maintain the DC-link voltage and set the power factor of the energy storage system. Pulse width modulation is employed to control the inverter which consequently regulates the speed and torque of the motor. However, some draw backs are spotted here. Mineshafts as we all know are cited outskirt of town sand cities thus making it very difficult and uneconomical to be transmitting energy from mineshaft that are distant away from residential.
In the same way, another area of interest where gravity storage is applied lately is the ocean shore. The latest ocean storage technology under rapid research and development is the DOGES (Deep ocean gravity storage.). It works basically via a combination of solar, mechanical and hydrostatic input. In the system, when energy is supplied to the photovoltaic cell which floats on the ocean surface, it is used to power a turbine or pump situated on the ocean bed hat is used to force water out of a storage tank on the ocean bed [17, 18].
The system works basically by harnessing the influence of potential energy, where the maximum stored energy is the difference in potential energy between an empty and a filled tank. The system is obviously technologically and economically viable for locations around the deep oceans of sufficiently large depths reaching 500 m. But the challenges to its implementation and operation are mostly Cavitation, mooring effect (which has to do buoyancy effect on the storage structure when pipes are empty under the ocean) and hydro turbine management which are quite expensive to deal with [17, 19].
Essentially, this research is geared towards designing a storage system using non-conventional methods and radical ideas with little similitude to previous research but totally different in functionality.
This design will store energy using the principle of potential energy conservation to store large amounts of energy during the daylight hours and release the stored energy during the night hours proportionately. The method adopted in this research requires a comparatively small battery for just smoothing out the power output (acting as a buffer and not primarily for storage purpose), only when it is required in the adjacent building with electrical loads as shown in the schematic in Fig. 2 below.
Methodology
A vee model approach will be adopted for the development of this design and its verification within along the design process. This model approach will analyse the different stages of the design the process taken to arrive at the design that make up the system lifecycle using simulation within all the stages of the design from specification and design concept to real-time simulation for rapid prototyping and design, testing and validation of the system functionality [16, 20, 21]. The chart below shows a detailed view of the path the model lifecycle will take from the start to validation of the system.
Conceptual design overview
The complete system is made up of solar panels rigidly fixed on the roof of a building. Electric cables of considerable length and diameter are used to connect the Panels via a diode to a charge controller augmented with an Arduino which would regulate charges supplied to the deep cycle batteries, the electric geared motor and standby load. The deep cycle battery is charged, and it is connected to an inverter which in turn is connected to AC loads in a given space (Fig. 3).
MATLAB simulation model of the design [30]
In the aspect of the system which aid the storage of energy by gravity, the aforementioned geared motor is mounted on a foundation connected to the spindle of a solenoid which does a reciprocating ram motion to give the geared motor a transverse motion back and forth to fit the geared motor shaft into a hollow shaft connected to an intermediate pulley when the solenoid is energized or de-energized. The pulley connected to the shaft is made up of two grooves. One act as the string wrap that carries the dead weight which falls under gravity when the solenoid retracts the geared motor shaft from the pulley shaft while the other connects to the dynamo pulley via a flat belt. Then, the dynamo is connected to the battery via cables of considerable length to avoid losses that may arise due to length and resistivity of the cables used.
System dynamics of model
See Fig. 4
Dynamic characteristics of the model design [33]
System modelling of proposed system using sysml models
Essentially, this modelling language software is a general purpose modelling language often known as Systems Modelling Languguage(Sysml) [22,23,24,25]. It basically allows for the representation of system designs using different diagrams that gives one an opportunity to have a simple understanding of design structures and dynamics. Some of the diagrams created on this platform includes Requirement Diagram, Block Definition Diagram/Internal Block Diagram Parametric Diagram, Activity Diagram/Sequence Diagram, etc. Figure 5 below shows some of the diagrams that have been created in this research to drive forward the idea of the design synthesis. Figure 5a is the Activity diagram of the design which depicts the function of every component of the system and the interdependence of each components of the design. Figure 5b is the block diagram of the system. This diagram gives an idea of all the components that make up the design model and their corresponding specifications. Lastly, Fig. 5c is the parametric diagram of the design model which shows the mathematical equations associated with the various components that are included in the design. There are other diagrams in the modelling language but this research will only adopt the three above to make relevant decisions.
Mathematical modelling
This aspect of the study defines the dynamics of each portion of the system mathematically. Here, each component that makes the design are related to other components using model equations and established mathematical constants and equations [22, 26]. The following below were the relevant design equations used for the study.
Kinetic energy of the rotating dynamo pulley
Motor Pulley Moment of inertia
Dynamo Pulley Moment of inertia
Kinetic Energy of the rotating Motor pulley
Required Inertia
Dead-weight travel height (H)
Mass required
Input Electrical Energy
Current needed to raise the load
Time duration for the weight to span through a specified height
Energy stored by the battery used
Time it takes to charge the battery
Energy Efficiency
Choice of belt length
Wire ropes and pulley drum capacity design
This design will be done based on uniform tension and normal drum rope winding condition. The wire ropes to be utilized in this in this design to bear the suspended weight will be designed to support their own weight and that of the suspended mass under a considerable depth.

Model load
TV 20 W on for 4 h per day = 20 Watts.
Radio 10 W on for 2 h per day = 10 Watts.
Water pump 20 W on for 2 h a day = 25 Watts.
Lighting 30 W on for 4 h per day = 20 Watts.
Fan 60 W on for 3 h per day = 20 Watts.
Power Requirement
Electric geared motor = 1.3 watts.
Model load = 95watts.
Total load = 100w atts approx.
Time it takes to charge the battery
For Lead Acid Deep cycle battery.
Required Charging current is usually calculated as 10% of the AH rating of a battery, this implies,
\({\mathbf{Charging}} \;{\mathbf{time}}\; {\mathbf{of}}\; {\mathbf{this}}\; {\mathbf{Battery}} = {\raise0.7ex\hbox{${200}$} \!\mathord{\left/ {\vphantom {{200} {20}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${20}$}} = 10\;{\text{h}}\).
This shows that if panels delivering up to 10 amperes of current are combined in series, it will take 5 h to charge up the battery and the extra hours will be used to lift the suspended weight via the current transmitted to the geared motor at the time (Table 1).
Model assumptions
-
1.
Each row in Tables 2 and 4 represent different test case scenarios of loading condition and requirement for a set a 10 sample data sets.
-
2.
Losses are accounted for in the system using some design decisions.
-
3.
The following parameters were taken as constants.
-
4.
Equations used only exemplifies a proof of concept.
-
5.
Each row in Table 2 and Table 4 represents a constant load application.
-
6.
Potential energy stored by the mass at a height is equal to the kinetic energy of the mass as it falls, and losses associated with energy conversion is neglected in this model.
Results and discussion
Table 2 below shows the information of a test model created to investigate the viability of the system. Here, a set of 10 different load current requirement were analysed highlighting the key parameters that determines functionality of the design and the resulting output electrical energy were investigated bearing in mind that some parameters referring to the mathematical modelling were kept constant as highlighted in session 3.4.1. However, some of the these parameters were actually observed to be constant as the study progresses. These parameters includes, Moment of Inertia (kg.m2) which was observed to be 16 × 10−6 and Inertia of Motor(M) Pulley (kg.m) was 288 × 10−5.
Figure 6 below is a chart showing potential sunshine hours and the cumulative size of panel required in wattage. The time duration in this case exemplifies the different regions around the world with different sunlight stretches associated with it and this therefore gives an hypothetical feasibility of this technology regionwise (Table 3).
It can be seen that solar panels with higher power ratings or a combination of mutiple panels will be required in regions of low sunlight stretches. Also, the regions with sunlight duration of one hour during the day will require solar PV panels of 500watts while those parts with 6 to 9 h of sunlight duration will require 80, 70 and 60 watts, respectively. This essentially proves the importance of effective utilization of this energy potential in continent like Asia or Africa with long sunlight stretches as they will require limited amount of panels consequently reducing the cost incurred on purchase of PV cells during set up.
Figure 7 is a chart showing the amount of current required to raise suspended weight of varying masses through a constant height. It can be seen that as the values of the masses increases, the current required gets larger. This shows that adopting the method of increasing the magnitude of the mass when setting up this storage system will assure reduction in capital cost as less solar PV cells will be required to supply sufficient amount of current needed for raising of the weight and charging the battery. The graph also shows the correlation between the mass required and the corresponding current requirement in the system. The chart clearly shows that as the mass to be lifted up a constant height increases the current required in the design also increases. This clearly explains that as the mass to be lifted through a certain height is increased a higher amount of energy will be needed to actualize the task of lifting. This definitely will go a long way to help in design synthesis during the design phase of a project that incorporates this technology.
Figure 8 is a chart showing the time duration for varying sizes of suspended weight raised up over a constant height when a constant current is assumed to be delivered by the solar PV cell. This simply proves that as the masses increases, the time taken for the weight to be raised to the top is also increased. This is depicted in the chart above which shows the straight-line plot increasing from left to right of the graph. For example, if there is a project which is planning to design for a test mass of 6 kg to be lifted over a specified height span, from this experiment we can safely say from our model study that it will take about 50 to 55 s for the mass to be lifted up to the top reference in order to potential energy.
Figure 9 above shows the efficiency based on the test parameters tends to be increase with a R-Square value of 0.9475 as the mass of the dead weight is increasing over a constant height. It can also be seen that the efficiency seems fairly constant at some points in the graph. This scenario occurs because as the mass increases while the travel height is still constant, the mass tends to get to the lower reference within a shorter time causing a transient energy dissipation. The output obtained when efficiency is calculated shows that high efficiency cannot be guaranteed by varying only the dead weight mass and leaving the travel height constant. More so, from Fig. 9, the energy output in this case study increases as the mass of the dead weight increases. This invariably accounts for the increase in efficiency reaching about 62% with a high correlation coefficient for this case study. This efficiency can be improved on if the design parameters are modified putting keys factors into consideration.
Figure 9.b above is the result of the MATLAB(simscape) simulation of the model in Fig. 3. This result simply shows the increase in speed of the dc motor in response to the falling weight. As the weight continues to fall, more currents are stored in the battery thereby increasing the speed of the motor. When the current in the battery starts reducing, the reverse of the representation on this graph will occur until the speed approaches zero signifying the current had been fully exhausted.
Model load requirement comparison between proposed system and existing system
From Table 2 above this study have analysed the effect of varying model parameters on the output electrical energy generated from the dynamo to the inverter in this research design. In the following Table 4, these same parameters are used to analyse existing system to reveal requirements that makes this proposed design a preferable alternative to it. Here, some realistic load requirements relative to real-life systems were analysed and the following were some of the assumptions and constants implemented in the investigation. Moreover, some of the parameters were not included in the table as highlighted in the mathematical model due to the resulting complexity of the data that will be presented. However, the ones presented are the key ones that interpretes the design system characteristics alongside the constants and assumptions.
From Table 4 above, it can be seen that the requirements of the proposed and existing system are simply affected by some key parameters which invariably influences our choices. For instance, for a load of 50 × 103 mA running for 10 h (3600 s), the proposed system will only need to provide a torque of 3.27 Nm and a height range of 66.1 × 104 m when a mass of 10 kg is lifted to give out power of 48kwh. Using the same load requirements, the existing solar system which basically store energy and deliver using battery will require 3 deep cycle batteries of 200 amperes-hour rating. This invariably shows outrightly on the cost effect on existing systems making it out of bound zone for a vast majority who appreciates this form of energy but lacks the capital to facilitate it. More importantly, the continent of Africa will be an ideal location for citing this proposed idea due to its huge sunlight potential and high volume of metal scrap materials which can be converted to suspended weights with reasonable torque value. At the moment not much has been done in harvesting, this wealth of energy principally because of this cost effect associated with its installation of the existing systems utilizing batteries primarily for storage purposes. Another issue of concern here will be the life span of the battery used in the systems. The life span of the battery in this proposed storage system will be longer since the battery utilized here will have a constant output hour duration irrespective of the energy output from the generating part of the system [19]. For the existing systems which utilizes multiple batteries for storage, the batteries tend to recalibrate due to changes in output hour duration and this reduces the lasting hours of the battery after a while thus giving an early wake up call for preventive maintenance.
More so, a faulty battery amongst the batteries used for storage in existing systems affects the entire battery system output and this is difficult to diagnose if the batteries used are much, but this proposed system have limited component and by simple visual inspection faulty part can be easily detected thus giving room for easy maintenance procedures. Lastly, a wrong battery connection (open circuit or short circuit) in the existing systems using batteries primarily for storage can result in power loss or fire outbreak, respectively, in worse case scenarios but the proposed system has a huge factor of safety terms of fire outbreak since batteries used are limited in number and are used primarily as buffers. Essentially, this system will be very effective in areas of large sunlight exposure duration to generate energy for farm works, domestic use and other commercial purposes. The unique characteristic of this system that makes it versatile is the fact that it is not restricted to a particular land topographical reference or expensive component design materials.
Limitations
The proposed model is a multi-state energy conversion system and a such will entertain losses along the line of generation, transmission, storage and consumption. The efficiency as observed in Fig. 9 above are not really large as desired in working systems. Essentially, this is due to the losses occurring in some part of the system during operation. Some of the likely areas where losses are occurring in the model system design include the following;
Belts and pulley drive
-
Friction occurring between the flat belt and pulley during power transmission (belts and pulley).
-
Rotational kinetic energy loss.
-
A coefficient of static friction of 0.30 between the belt and pulley material incurring some percentage loss in the total power is assumed in this design since. The slip between the belt and pulley deprives the transmission of total power. Hence, this is another reason for drop in efficiency.
Electrical cables
All cables have losses and will ultimately limit the performance of a system. However, the magnitude of the loss depends on the cable specifications.
Electrical resistance in wires utilized for establishment of connection between the various components that make up the system entertains I2R losses (in form of heat).
Chemical reactions in battery
During the charging and discharging of the batteries used as buffer, some losses also occur since the chemical reactions(electrolysis) associated with the process is not perfectly reversible. During the conversion of chemical energy to electrical energy, the conversion factor for lithium ion batteries is between 0.8 and 0.9 [27, 28]. This means there are losses between 0.1 and 0.2 which are not accounted for that can be seen as heat since energy cannot be destroyed (first law of thermodynamics).
Energy conversion process
Hysteresis losses occurs in the following processes in the model operation [29];
-
When converting potential energy into electrical energy with a generator (dynamo).
-
Converting electrical energy into potential energy using the geared motor.
-
Converting potential energy into kinetic energy and back which loses energy from air resistance in the stator.
Based on the physics of energy conservation and conversion, the maximum kinetic energy a mass can gain is equal to the potential energy it can lose. In the proposed design, the total energy loss in the conversion processes listed above but not accounted therefore contribute to the agents of inefficiency index.
Conclusion
The alternative gravity storage system is very simple, and all its components are quite reachable in terms of availability in the market. The basic difference between this alternative gravity storage system and other gravity storage techniques currently in the literature is that this concept can be applied on both domestic for household utilization or on a commercial scale depending on the electricity demand of the area applied [30, 31, 32]. Also, this module can be easily constructed to demonstrate principle of conversion of potential energy via gravitational influence on various form of energy on small scale to students in colleges and colleges, design manufacturers in the industry, exhibition to the general public, etc. Essentially, due to the importance and rising necessity for energy storage in combating climate issues as it brings about the integration of renewable energy into the national grid network, this work designed a new storage method that is environmentally friendly and reduce the pathway to cost effects. Hence, a concept approach to optimally harness gravity storage was proposed. The technical analysis in the work constitute the design of the optimal that could generate and store energy in the light of all constraints involved. This storage system has been described in this context using necessary performance parameters associated with energy storage which include energy efficiency value (charge/discharge rate), System capacity, etc. These aforementioned parameters and others listed in the work were used as measures to identify the viability of the storage system. Subsequent optimization of the design and sizing of this storage method might enable the gravity storage approach to compete favourably with current storage solutions already in the market.
Further research on this subject area could compromise the methodology on sizing, configuration, area of application, etc. For modelling other applications in the grid reference. Essentially, the model could be analysed for parameters that this design did not put into consideration. The model could be analysed using other constrain and assumptions which includes mainly the demand and transmission at different time frame. Also, on a commercial scale, a magnetic clutch can be used between the geared motor and the pulley carrying the weight to facilitate quick response time. Also, a high frequency capacitor or alternators that delivers up to 40amperes of current like the ones used in vehicles can be considered in place of the dynamo to facilitate fast charging of the battery for a more larger system specification.
Abbreviations
- B :
-
Barrel diameter (mm)
- β :
-
Constant developed according to rope diameter for rope under loading condition
- C :
-
Centre distance of the connected pulleys (mm)
- D1:
-
Diameter of the intermediate pulley (mm)
- D2:
-
Diameter of dynamo pulley (mm)
- ε :
-
Efficiency (%)
- h :
-
Desired winding depth around the barrel (mm)
- H :
-
Dead-weight travel height (mm)
- I :
-
Load current (mA)
- I R :
-
Inertia required (kgm)
- J d :
-
Moment of inertia of dynamo pulley (kgm2)
- J m :
-
Moment of inertia of motor pulley (kgm2)
- K.E m :
-
Kinetic energy of the rotating Motor pulley (kgm2/s2)
- K.E d :
-
Kinetic energy of the rotating dynamo pulley (kgm2/s2)
- L :
-
Length of belt required (mm)
- Lw :
-
Length of rope wind round the drum (mm)
- m m :
-
Mass of motor pulley (g)
- m d :
-
Mass of dynamo pulley (g)
- m R :
-
Suspended mass to be lifted (mm)
- P.E :
-
Potential energy (kgm2/s2)
- V :
-
Load voltage (V)
- ω d :
-
Angular velocity of dynamo pulley (rad/s)
- W :
-
Distance between flanges (mm)
- r m :
-
Radius of motor pulley (mm)
- T :
-
Time duration for the weight to span through a specified height (s)
- α m :
-
Angular Acceleration of Motor pulley (rad/s2)
References
Mahlia, T., Saktisahdan, T., Jannifar, A., Hasan, M., Matseelar, H.: A review of available methods and development on energy storage; technology update. Renew. Sustain. Energy Rev. 33, 532–545 (2014). https://doi.org/10.1016/j.rser.2014.01.068
Razykov, T., Ferekides, C., Morel, D., Stefanakos, E., Ullal, H., Upadhyaya, H.: Solar photovoltaic electricity: current status and future prospects. Solar Energy 85(8), 1580–1608 (2011). https://doi.org/10.1016/j.solener.2010.12.002
U. E. P. A. M. S. Waste: U.S. Environmental Protection Agency, 5 February 2011. [Online]. Available: https://www.epa.gov/facts-and-figures-about-materials-waste-and-recycling/advancing-sustainable-materials-management-0. Accessed 6 Mar 2019
Vazquez, S., Lukic, S., Galvan, E., Franquelo, L., Carrasco, J.: Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 57(12), 3881–3895 (2010). https://doi.org/10.1109/tie.2010.2076414
Rehman, S., Al-Hadhrami, L., Alam, M.: Pumped hydro energy storage system: a technological review. Renew. Sustain. Energy Rev. 44, 586–598 (2015). https://doi.org/10.1016/j.rser.2014.12.040
Fyke, A.: The fall and rise of gravity storage technologies. Joule 3(3), 625–630 (2019). https://doi.org/10.1016/j.joule.2019.01.012
Berrada, A., Loudiyi, K., Garde, R.: Dynamic modeling of gravity energy storage coupled with a PV energy plant. Energy 134, 323–335 (2017). https://doi.org/10.1016/j.energy.2017.06.029
Berrada, A., Loudiyi, K., Zorkani, I.: Toward an improvement of gravity energy storage using compressed air. Energy Procedia 134, 855–864 (2017). https://doi.org/10.1016/j.egypro.2017.09.542
Botha, C., Kamper, M.: Capability study of dry gravity energy storage. Energy Storage 23, 159–174 (2019)
Solar energy and energy storage devices. Solar Energy 3(3), 48 (1959). https://doi.org/10.1016/0038-092x(59)90150-1
U. E. P. Agency: Enforcement alert. 12 March 2002. [Online]. Available: https://www.call2recycle.org/doc_lib/EPA%20Battery%20Alert.pdf. Accessed 6 Mar 2019
Blair, C.: Gravicity technology. Gravicity [Online]. Available: https://www.gravitricity.com/#the-technology. Accessed 11 Feb 2019
Hunt, J.D., Zakeri, B., Falchetta, G., Nascimento, A., Wada, Y., Riahi, K.: Mountain gravity energy storage: a new solution for closing the gap between existing short- and long-term storage technologies. Energy 190, 116–419 (2020)
Pedretti, A.: Quartz. 18 August 2018. [Online]. Available: https://qz.com/1355672/stacking-concrete-blocks-is-a-surprisingly-efficient-way-to-store-energy/. Accessed 11 Feb 2019
Morstyn, T., Chilcott, M., Mcculloch, M.: Gravity energy storage with suspended weights for abandoned mine shafts. Appl. Energy 239, 201–206 (2019). https://doi.org/10.1016/j.apenergy.2019.01.226
Emrani, A., Berrada, A., Bakhouya, M.: Modeling and performance evaluation of the dynamic behavior of gravity energy storage with a wire rope hoisting system. J. Energy Storage 33, 102–154 (2021)
Cazzaniga, R., Cicu, M., Marrana, T., Rosa-Clot, M., Rosa-Clot, P., Tina, G.: DOGES: deep ocean gravitational energy storage. J. Energy Storage 14, 264–270 (2017). https://doi.org/10.1016/j.est.2017.06.008
Hou, H., Xu, T., Wu, X., Wang, H., Tang, A., Chen, Y.: Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 271, 115052 (2020)
Garg, S., Kalpesh, G.: A review on energy storage systems for mitigation power fluctuations in wind turbine based power system. Int. J. Trend Sci. Res. Dev. 1(4), 414–419 (2017). https://doi.org/10.31142/ijtsrd170
Zahedi, S.A., Demiral, M., Roy, A., Silberschmidt, V.V.: FE/SPH modelling of orthogonal micro-machining of fcc single crystal. Comput. Mater. Sci. 78, 104–109 (2013)
Zahedi, S.A., Babitsky, V.: Modeling of autoresonant control of a parametrically excited screen machine. J. Sound Vib. 380, 78–89 (2016)
Bougain, S., Gerhard, D.: Supporting product design decision with a SysML design history Assistant. Procedia CIRP 91, 255–260 (2020)
Oladapo, B.I., Zahedi, S.A., Vahidnia, F., Ikumapayi, O., Farooq, M.U.: Three-dimensional finite element analysis of a porcelain crowned tooth. Beni-Suef Univ. J. Basic Appl. Sci. 7(4), 461–464 (2018)
Malachi, O.B., Oladapo, B.I., AbolfazlZahedi, S., Omigbodun, F.T., Oshin, E.A., Adebiyi, V.A.: Microstructural evaluation of aluminium alloy A365 T6 in machining operation. J. Mater. Res. Technol. 8(3), 3213–3222 (2019)
Oladapo, B.I., Zahedi, S., Adeoye, A.: 3D printing of bone scaffolds with hybrid biomaterials. Compos. B Eng. 158, 428–436 (2019)
Bowoto, O.K., Oladapo, B.I., Zahedi, S.A., Omigbodun, F.T., Emenuvwe, O.P.: Analytical modelling of in situ layer-wise defect detection in 3D-printed parts: additive manufacturing. Int. J. Adv. Manuf. Technol. 111, 2311–2321 (2020)
Tesla: Tesla Energy, Tesla, 2019. [Online]. Available: https://www.tesla.com/energy. Accessed 13 Mar 2019
Silakhori, M., Jafarian, M., Arjomandi, M., Nathan, G.: Thermogravimetric analysis of Cu, Mn Co, and Pb oxides for thermochemical energy storage. J. Energy Storage 23, 138–147 (2019). https://doi.org/10.1016/j.est.2019.03.008
Saif-Ul-Rehman, M.: Prospects and limitations of solar energy utilization in developing countries. Solar Energy 11(2), 98–108 (1967). https://doi.org/10.1016/0038-092x(67)90049-7
Bowoto, O.K., Omigbodun, F.T., Nimako, P.A., Oshin, E., Omonigho, E.P.: Matlab based model design optimization of vehicle drivetrain of advanced vehicle simulation. Int. J. Mech. Eng. 21(6), 20–36 (2019). https://doi.org/10.14445/23488360/IJME-V6I6P105
Energysage: Smarter energy decisions, energysage, 12 Feburary 2019. [Online]. Available: https://www.energysage.com/solar/solar-energy-storage/what-do-solar-batteries-cost/. Accessed 12 Mar 2019
Ferreira, H., Garde, R., Fulli, G., Kling, W., Lopes, J.: Characterisation of electrical energy storage technologies. Energy 53, 288–298 (2013). https://doi.org/10.1016/j.energy.2013.02.037
Bowoto, O.K., Oladapo, B.I., Nimako, P.A., Omigbodun, F.T., Emenuvwe, O.A.: Arduino fault tolerant system, internet of things (IoT). Preprints 2019, 2019060034. https://doi.org/10.20944/preprints201906.0034.v1
Acknowledgements
We appreciate the funding/financial support received from the Higher Education Innovation Fund (HEIF) of De Montfort University, Leicester, United Kingdom, under Research Project No. 0043.06.
Author information
Authors and Affiliations
Contributions
Oluwole K. Bowoto involved in conceptualization, methodology, software, writing—original draft and project administration. Omonigho P. Emenuvwe participated in review & editing, formal analysis, investigations, data curation and validation. Meysam N. Azadani involved in visualization, data curation and investigation.
Corresponding author
Ethics declarations
conflict of interest
We, hereby, affirm that there is no conflict of interest.
Ethical statement
The authors declare no ethical issue; the study was conducted in full agreement with ethical standards. Also, the manuscript is neither under review nor published elsewhere.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bowoto, O.K., Emenuvwe, O.P. & Azadani, M.N. Gravitricity based on solar and gravity energy storage for residential applications. Int J Energy Environ Eng 12, 503–516 (2021). https://doi.org/10.1007/s40095-021-00393-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-021-00393-1